大椭圆线椭球高斯投影在高速铁路工程中的应用

2018-02-28冯黎刚姚德新金立新

测绘通报 2018年1期

冯黎刚，姚德新，金立新

(1. 兰州交通大学测地学院，甘肃兰州 730070; 2. 甘肃铁道综合工程勘察院，甘肃兰州 730000)

随着高速铁路等长线工程建设越来越多，对其基础及轨道的施工精度的要求也越来越高。在高速铁路线路测量中，存在测区远离中央子午线与平均高程较大的问题，若直接使用传统的横轴高斯投影方法对测区控制点进行投影转换，就会使得投影时投影长度变形值很大。另外，对于东西跨度较长的高铁线路，为了控制边长的投影变形，往往需要划分较多投影带，建立众多的独立坐标系，不仅使得数据转换时的计算量突增，而且容易给整条铁路施工带来不便。基于这种情况，本文基于最小二乘估计、非线性规划最优理论等相关数学方法提出一种处理线路测区的控制点数据的方法——大椭圆线椭球高斯投影法，并通过工程实例检验其在东西走向长线工程中的优越性、实用性。

1 基础椭球(E0)向大椭圆椭球(E1)的转换

1.1 建立大椭圆线椭球

所谓基础椭球向大椭圆线椭球的转换，其实质就是根据基础椭球的几何参数求解大椭圆椭球的几何参数[1-4]。首先找出沿线路延伸方向附近过原点的大椭圆线，将基础椭球经过旋转、变形[5-6]建立以大椭圆线为中央子午线的新椭球；其次，根据控制点在E0中的坐标和几何参数求E1的几何参数。在基础椭球中，某一点的空间直角坐标与大地坐标的转换关系为[7]

(1)

式中，N为大地纬度B对应的卯酉圈曲率半径；e为基础椭球第一偏心率。

大椭圆椭球与基础椭球间的转换模型如图1所示，已知QMQ′为基础椭球上某一线路附近的大椭圆，线路测区内一点P(Bi，Li，Hi)的空间直角坐标为P(Xi，Yi，Zi)。设γ=(m1，m2，m3)为大椭圆的法向量，根据空间平面的点法式方程得大椭圆所在的平面方程为

m1Xi+m2Yi+m3Zi=0

(2)

然后以大椭圆QMQ′为中央子午线建立大椭圆线椭球，则由式(2)得到关系式

(3)

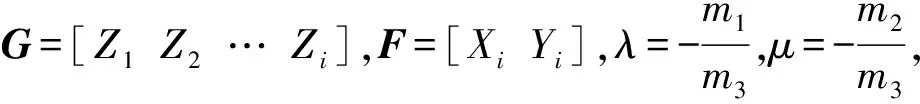
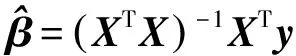
(4)

由式(4)求得λ、μ，从而解出大椭圆的法向量之间的比例关系。

在大椭圆QMQ′中，Q点为大椭圆的极点，M点为大椭圆与基础椭球赤道面的交点，则OM为长半轴，OQ为短半轴，将椭圆绕OQ旋转便可得到所需的大椭圆线椭球E1。作OU垂直OQ和OM组成的大椭圆面，即可建立以OM为X1轴、OU为Y1轴、OQ为Z1轴的大椭圆线椭球的空间直角坐标系O-X1Y1Z1。坐标系转换具体表现形式如图1所示。

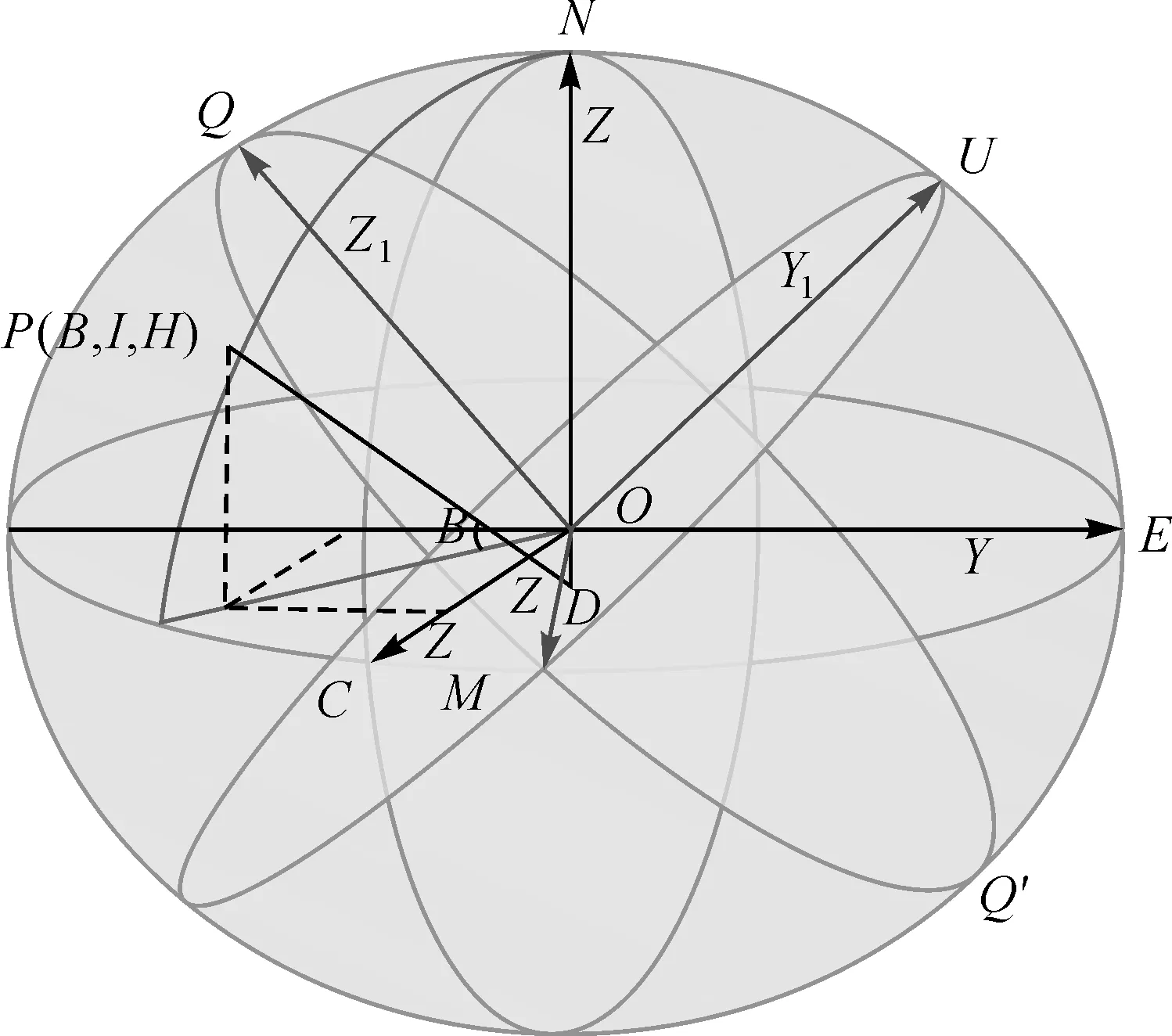
图1 大椭圆椭球与基础椭球转换模型

1.2 求解大椭圆线椭球的几何参数

从上文可知，Q点既是大椭圆的极点又是基础椭球上的一点，因此它既满足大椭圆的平面方程又满足基础椭球的方程。

当Q为基础椭球上的一点时，由大地测量学的知识可知，地球基础椭球是经过适当选择的旋转椭球，方程为

(5)

当Q点为大椭圆面的极点时，所满足的方程为

m1X+m2Y+m3Z=0

(6)

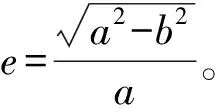
结合式(5)、式(6)可得化简后的方程为

(1-e2+λ2)X2+1-e2+μ2Y2+2λμXY=

a2(1-e2)

(7)

因Q点为大椭圆的极点，即大椭圆的最高点，因此上述问题可看作在一定的约束条件下求目标函数Z=λX+μY的最值问题,根据二次曲线不变量法可以判定出式(7)所代表的曲线为椭圆，且以式(7)为约束条件。

依据相关数学理论，上述问题属于一个非线性规划模型，根据非线性规划模型约束最优化方法中的拉格朗日乘子法可以求出目标函数Z最大值及取最大值时X和Y的值，即

(8)

在基础椭球的空间几何关系中，大椭圆面QMQ′是经过原点的，那么以大椭圆面为中央子午线建立的大椭圆线椭球的长半轴长度与基础椭球的长半轴长度是一致的，即a1=a,而短半轴b1的长度可以根据Q点在基础椭球中的三维坐标值求出，即

(9)

大椭圆线椭球E1的第一偏心率平方为

(10)

大椭圆线椭球E1的第二偏心率平方为

(11)

通过上述公式即可求出大椭圆椭球的基本几何参数，如长半轴、短半轴及偏心率等，基本完成大椭圆椭球的构建。

2 大椭圆椭球空间直角坐标的计算

由空间解析几何的知识可知，基础椭球与大椭圆椭球空间直角坐标系之间的转换属于一种正交变换，其变换矩阵可由大椭圆线上的点在E0中的纬度、经度、大地方位角的方向余弦表示，然后利用大椭圆的法向量来表示经纬度及大地方位角的方向余弦。因此可得到基础椭球空间坐标O-XYZ与大椭圆椭球坐标O-X1Y1Z1间转换关系式[1]为

(12)

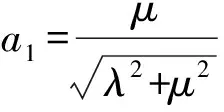
将基础椭球的空间直角坐标转换为大椭圆椭球的空间直角坐标后，还需要将其转换成大椭圆线椭球的大地坐标。在解决大椭圆椭球空间坐标向大地坐标的转换问题时，Bowring提出的改进算法[8]是最佳的，对于任何位置上的点，计算的大地纬度精度均高于10-7，公式为

(13)

通过式(13)即可计算出点在大椭圆椭球的经纬度及大地高。

3 变形大椭圆椭球(E2)的构建

3.1 变形大椭圆椭球的大地坐标

将基础椭球旋转建立大椭圆椭球E1后，还不能直接进行高斯投影。因为当测区内有的点在大椭圆椭球上的大地高过大时，直接进行投影会导致投影的综合变形过大，反而使得改进的方法失去其在减小投影变形中的优越性。因此，为了减小投影时的横坐标ym及点的大地高，通常要对大椭圆椭球进行椭球变换。常见的椭球变换方法有膨胀法、平移法和变形法[9-10]。本文采用变形法对大椭圆椭球进行变换得到变形大椭圆椭球E2。

对于大椭圆椭球的变换模型，一般采用广义大地坐标微分公式[7]进行分析和研究。椭球变形法不会引起大地经度的变化，但对大地纬度和大地高有较大的影响，且会使得椭球的长轴半径和扁率有一定的变化。由地球椭球基本几何参数之间的关系可知：e2=2α-α2⟹de2=21-αdα，因此广义大地坐标微分公式可简化为

(14)

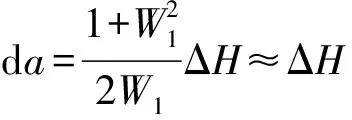
通过式(14)并结合点在E1中的大地坐标即可求出点在变形大椭圆椭球E2上的大地坐标。

3.2 变形大椭圆椭球向高斯面的投影变形

取一个圆柱(或椭圆柱)横套在E2外面，并保证E2的中央子午线(即大椭圆线)与圆柱面(或椭圆柱面)相切，然后将圆柱面(椭圆柱面)展开成平面，即得到所需的E2的横轴高斯投影，相对于基础椭球E0来说属于斜轴高斯投影。

高斯投影属于横轴椭圆柱等角投影，在其投影过程中主要存在两方面的长度变形：一是将地面的观测长度归算至参考椭球面上而产生的高程化改正；二是参考椭球面上的长度投影到高斯面上而产生的投影长度变形。投影过程中长度的综合变形[7,11-12]为

(15)

式中，R为归算边方向法截弧的曲率半径；Hm为测区边两端点的平均大地高程；ym为测区边投影后两端点的横坐标平均值；S为参考椭球面上的长度。

4 实例分析

现取某段高速铁路的CPI控制点数据。该高铁线路走向为东西方向，线路测区位于东经109°38′—121°20′、北纬31°09′—32°02′。已知线路部分CPI控制点在WGS-84椭球中的空间直角坐标和大地坐标见表1。

表1 CPI在WGS-84中的大地坐标

根据《高速铁路工程测量规范》的内容，测区内控制网的投影长度变形值在投影过程中不能超过10 mm/km。如果按照常规的高斯投影方法，则该段控制网至少要划分为3个投影带才能满足要求，投影带划分方法和投影过程中产生的综合变形见表2。

从表2可以看出，采用传统的高斯投影方法时，不仅要对测区进行分带处理，而且综合长度变形值也是勉强符合规范要求。

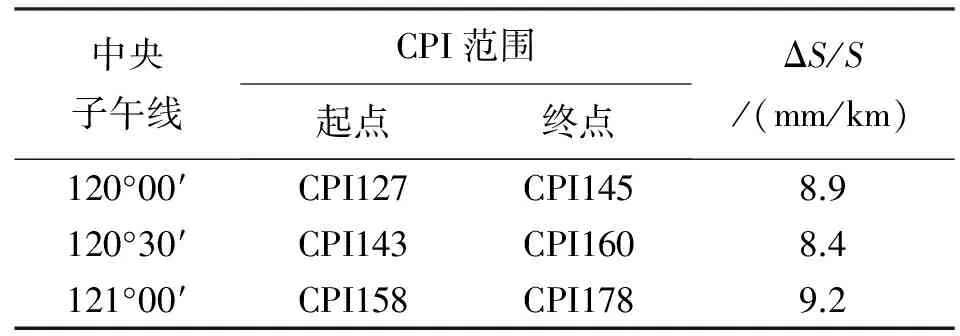
表2 投影带划分及其综合变形

下面用大椭圆椭球的方法来解算分析同一问题，具体步骤如下：

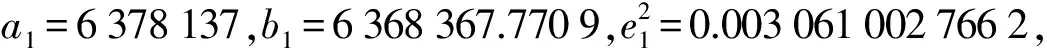
(2) 以CPI 127点为基准点，令ΔH=12 m对大椭圆椭球进行变形，解得长半轴和第一偏心率的改变量为：da≈ΔH=12 m，de2=-0.000 000 005 752。从而可以求得控制点CPI 127—CPI178在变形大椭圆椭球E2的大地坐标，然后对E2椭球进行横轴高斯投影，投影结果及其长度变形结果见表3。

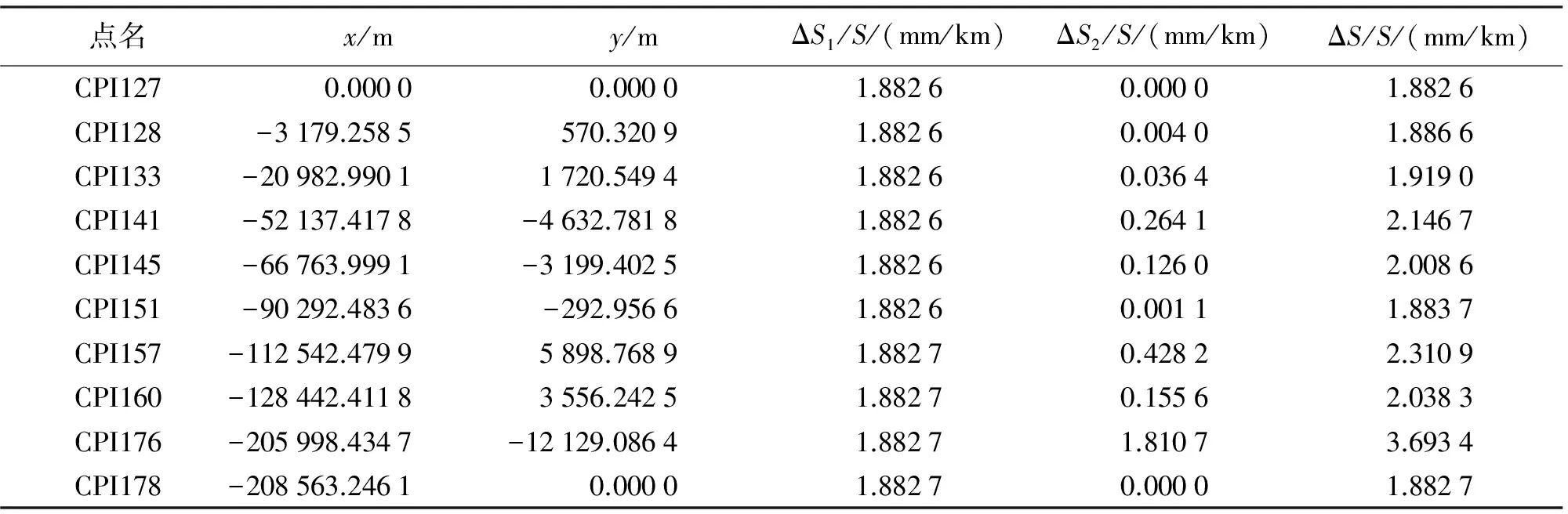
表3 大椭圆变形椭球投影结果

5 结语

通过实例对两种投影方法的结果进行分析比较后可以看出，大椭圆线椭球高斯投影的方法在投影时最大长度变形值不超过5 mm/km，而传统高斯投影法的长度变形值在8～10 mm/km之间。因此，可以看出大椭圆线椭球高斯投影法在解决东西方向铁路线路投影变形问题时不仅避免了投影分带，而且其精度要优于传统的高斯投影方法。

[1] 金立新，付宏平.法截面子午线椭球高斯投影理论[M].西安：西安地图出版社,2012.

[2] 李全海.斜圆柱投影及其对GPS空间坐标的转换模型[J].同济大学学报(自然科学版)，2002,30(1):106-110.

[3] 冯上朝，张宗团.斜轴圆柱投影在高速铁路测量中的应用研究[J].矿山测量，2012(3):86-87.

[4] 王文庆，帅明明，龚俊.斜轴墨卡托投影在东西走向高速铁路中的应用[J].地理空间信息，2013,11(4):152-153.

[5] 丁士俊，畅开蛳，高锁义.独立网椭球变换与坐标转换的研究[J].测绘通报，2008(8):4-7.

[6] 于亚杰，赵英志，张月华.基于椭球膨胀法实现独立坐标系统的建立[J].测绘通报，2011(12)：33-36.

[7] 孔祥元，郭际明，刘宗泉.大地测量学基础[M].武汉：武汉大学出版社,2001.

[8] 黄谟涛，翟国君，管铮，等.空间直角坐标与大地坐标的转换[J].测绘科学技术学报，1998,15(3)：164-168.

[9] 李世安，刘经南，施闯.应用GPS建立区域独立坐标中椭球变换的研究[J].武汉大学学报(信息科学版)，2005,30(10)：889-891.

[10] 王磊，郭际明，申丽丽，等.顾及椭球面不平行的椭球膨胀法在高程投影面变换中的应用[J].武汉大学学报(信息科学版)，2013,38(6):725-733.

[11] 田林亚，张勇，热比亚，等.高速铁路测量中高斯平面坐标与斜轴墨卡托平面坐标的转换[J].铁道标准设计，2013(4):13-16.

[12] 白建军，宋伟东，马维若.高速公路平面控制测量中投影问题的分析[J].测绘科学，2006,31(4):133-134.