交流接触器电压暂降非单调抗扰特性分析

钟 庆, 吴浩波, 贺 哲, 许 中, 莫文雄

(1. 华南理工大学电力学院, 广东省广州市 510640; 2. 广州供电局有限公司, 广东省广州市 510410)

0 引言

开关设备在实现系统的高效控制、保护及信号传递中起着重要作用。在各种开关设备中,交流接触器以具有可远程操作、控制简单等优点,可与其他器件配合实现定时操作、欠压保护及各种定量控制等功能,因此广泛应用于各种连续生产的工业场合[1]。但由于交流接触器容易受到电压暂降影响而跳脱,使得工业生产过程中断,造成停运或紊乱,给企业带来巨大的经济损失[2-3]。因此,研究交流接触器的电压暂降抗扰特性具有很强的实际应用价值。

目前,国内外学者主要从实际测试和仿真分析两个方面对交流接触器的电压暂降响应特性开展了研究工作。文献[4]在PSCAD/EMTDC平台上搭建了接触器的电磁暂态模型,基于仿真结果绘制了在不同电压暂降起始角下的电压耐受曲线(voltage tolerance curve,VTC),以此分析电压暂降起始角对交流接触器响应特征及对电压暂降穿越能力的影响。文献[5]建立了交流接触器的机械运动方程,求解拉格朗日函数,并在MATLAB/Simulink模块中搭建其仿真模型,对接触器线圈发生电压暂降时的响应特性及触点分断情况进行研究。文献[6]以交流接触器的控制线圈电流为观测角度,对两款不同型号接触器分别进行试验测试并绘制了接触器的VTC。文献[7]建立交流接触器的电磁模型,通过仿真得到接触器电磁吸力变化曲线,结合实测数据,进而得到了交流接触器的VTC。文献[3,8]综合选取多款接触器作为测试样品,以多纬度对比总结交流接触器的抗扰特性,并对接触器在非矩形电压暂降下的响应特征进行分析。

VTC是描述设备电压暂降抗扰特性的主要手段之一。根据VTC的定义可知,曲线下方的区域属于设备无法耐受的区域。一般认为VTC具有单调性,即对于残余电压越小的电压暂降,设备可耐受的持续时间越短。但文献[3,6-8]中的大量测试结果表明,不同类型的交流接触器均具有以下电压暂降抗扰特性:当电压暂降起始角为0°时,交流接触器在残余电压为50%时,能耐受的持续时间约为20 ms,而在残余电压为20%时,能耐受的持续时间约为70 ms。该特性与传统VTC的定义不同,在本文称之为电压暂降非单调抗扰特性。由于交流接触器电压暂降非单调抗扰特性的存在,使得交流接触器电压暂降免疫度的评估结果与实际情况产生偏差,难以做到有效地界定设备或系统的受扰程度,因此需要深入了解电压暂降非单调抗扰特性产生的原因。但目前国内外尚未开展该方面的研究工作。

为此,本文以迎击式交流接触器为研究对象,从控制线圈的电气特性出发,研究交流接触器电压暂降非单调抗扰特性的产生原因。首先,构建了交流接触器的数学模型,包括控制线圈的电气特性和交流接触器的机械运动特性;其次,分析了电压暂降时控制线圈的等值电路模型和数学模型,通过求解不同电压暂降起始角时控制线圈电流和交流接触器弹簧压缩距离,确定交流接触器是否跳脱,从而确定交流接触器的电压暂降抗扰特性,并从理论上分析了电压暂降非单调抗扰特性产生的原因;最后,通过实验观察控制线圈的电流波形,验证了本文研究结果的正确性。

1 交流接触器的数学模型

迎击式交流接触器结构原理图如附录A图A1所示[9]。图中:M1为动触头支架质量；M2为动衔铁芯质量；K为反力弹簧；X1为交流接触器的控制线圈；X2为分磁环线圈；x为弹簧压缩距离,可表示动、静触头之间的距离。在控制线圈上施加电压,产生磁通,形成电磁力,带动触头吸合。当发生电压暂降时,控制线圈电流将发生变化,产生的电磁力减小。在弹簧力作用下,可能导致动、静触头分开,从而引发交流接触器跳脱。

交流接触器分磁环主要是对控制线圈电流衰减起延后作用,使得接触器的电压暂降耐受时间增长以及极限耐受残余电压幅值增大,但对交流接触器“非单调”特性影响不大。因此,本文在建立数学模型分析电压暂降非单调抗扰特性时不考虑分磁环影响。交流接触器的吸合过程受机械、电和磁等方面约束,可用电压方程和机械运动方程描述。根据基尔霍夫电压定律,可列写出控制线圈的电压方程为:

(1)

式中:u和i分别为控制线圈的电压和电流;R为控制线圈电阻;L为控制线圈电感。

另外,根据磁路欧姆定律可知控制线圈的磁通φ为:

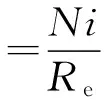
(2)

式中:N为控制线圈匝数;Re为铁芯磁阻。

铁芯磁阻Re与弹簧压缩距离x相关,计算公式为:

(3)

式中:A为线圈有效截面积;μ0为真空磁导率:μr为铁芯相对磁导率:D为交流接触器吸合时的弹簧压缩距离;le为磁路长度。

因此,控制线圈电感L的计算公式为:

(4)

根据牛顿第二运动定律,可列出交流接触器的运动方程为[10-11]:

(5)

式中:Fx和Fy分别为铁芯所受的电磁力和弹簧力。

电磁吸力Fx的计算公式为:

(6)

而弹簧力Fy的计算公式为:

Fy=kx

(7)

式中:k为弹簧的弹力系数。

将式(2)、式(6)和式(7)代入式(5),可获得交流接触器弹簧压缩距离与控制线圈电流之间的关系表达式为:

(8)

由此可知,交流接触器的数学模型包含式(1)所示电压方程和式(8)所示机械运动方程。从数学模型可知,控制线圈电流瞬时值i越大,电磁力越大,维持吸合状态的能力越强。需要注意的是,在交流接触器中,弹簧压缩距离只能在一定范围内变化。本文认为在吸合状态下,弹簧压缩距离达到上限值xmax=D,在完全释放状态下,弹簧压缩距离达到下限值0。

2 电压暂降时控制线圈电流计算

当发生电压暂降时,控制线圈中电气量变化过程可通过图1所示的等值电路模型进行描述。图中用一个R和L的阻感串联回路表示交流接触器控制线圈。Um为暂降前电压幅值,Um′为残余电压幅值。用Um和Um′之间的切换表示电压暂降。

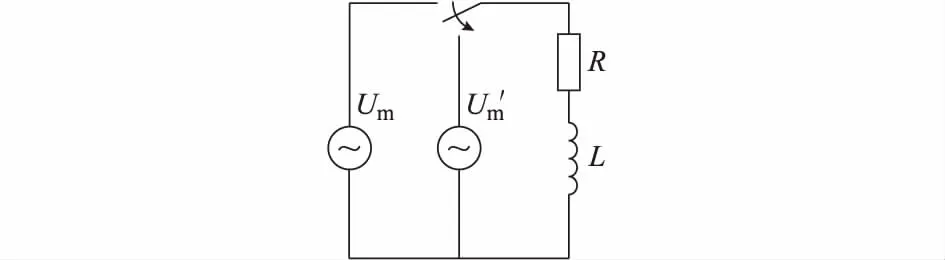
图1 电压暂降时控制线圈的等值电路Fig.1 Equivalent circuit of control coil during voltage sag

电压暂降发生时,交流接触器控制线圈的电压方程为:

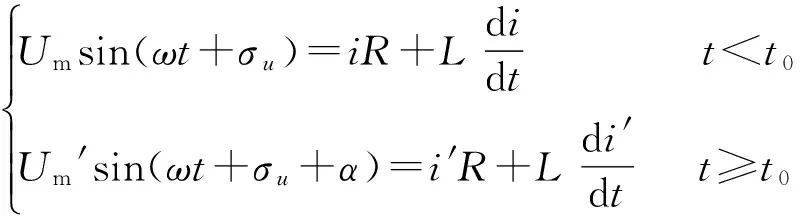
(9)

式中:t0为暂降发生时刻;ω为角频率;σu为暂降前电压相角;α为电压暂降的相位跳变值。

根据三要素法求解出电压暂降发生后控制线圈的电流表达式为:

(10)

式中:i(t0+)为控制线圈电流的初值;i∞为控制线圈电流的终值;τ为时间常数。

(11)

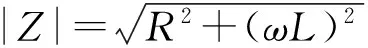
由等值电路可知,电流终值为:

(12)

因此

(13)

从而可知发生电压暂降时,控制线圈电流的非周期分量为:

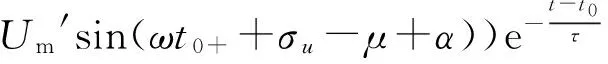
(14)

控制线圈的非周期分量指数衰减,时间常数为τ=R/L。初值大小与电压暂降的残余电压、起始角、控制线圈阻抗大小及相位跳变角有关。

由于控制线圈中电感远大于电阻,可近似认为电流相位滞后电压90°,即μ≈90°。当电压暂降起始角为0°时,即ωt0++σu=0°,控制线圈电流非周期分量的初值为inp(t0+)=(Um-Um′cosα)/|Z|,此时控制线圈电流非周期分量非常明显,且残余电压Um′越小,控制线圈电流非周期分量初值越大。当电压暂降起始角为90°时,即ωt0++σu=90°,控制线圈电流非周期分量的初值为inp(t0+)=(Um′sinα)/|Z|,暂降发生后控制线圈电流的非周期分量的初值较小,其电流值主要由周期分量确定。控制线圈电流瞬时值的变化将决定弹簧压缩距离的变化,从而决定交流接触器是否会跳脱。

电力系统中电压暂降相位跳变角一般小于30°,即α<30°。由式(12)可知,相位跳变角α对控制线圈电流周期分量的幅值没有影响。在残余电压较小时,相位跳变角对控制线圈电流非周期分量初值影响也不大。而电压暂降非单调抗扰特性一般发生在残余电压较小的电压暂降事件中,因此下文中将不考虑相位跳变。

3 交流接触器的数学模型求解方法

在交流接触器的数学模型中,铁芯电阻Re和控制线圈电感值L等参数与弹簧压缩距离x相关。因此,在交流接触器吸合和释放过程中,由于x的变化,交流接触器呈现复杂的非线性关系,难以解析求解,可通过数值算法迭代进行求解,求解过程见附录A图A2。

选取一定的时间步长Ts,认为在时间步长内,弹簧压缩距离保持不变。初始状态为吸合状态,弹簧压缩距离x为最大值xmax,计算得出交流接触器控制线圈电感L和控制线圈电流i,从而可以计算获得弹簧压缩距离x。当交流接触器保持吸合或完全跳脱状态时,认为弹簧压缩距离不变,否则更新弹簧压缩距离和电源电压进行下一步迭代求解,一直到计算时长Tend,最终输出弹簧压缩距离与时间的关系。通过求解弹簧压缩距离,可以判断在电压暂降作用下,交流接触器是否会跳脱。

4 交流接触器电压暂降非单调抗扰特性

为分析交流接触器电压暂降非单调抗扰特性,给定交流接触器参数如下:额定电压为220 V,额定频率为50 Hz,线圈匝数为500匝,M1+M2=0.4 g,A=8.814×10-4m2,D=7 mm,μ0=4π×10-7H/m,相对磁导率μr=8 000 H/m,磁路长度le=0.018 m,弹簧系数k=4 410 N/m。控制线圈电流t0+时刻的电流值和周期分量幅值的计算结果见附录A表A1。在电压暂降残余电压较小时,控制线圈非周期分量值较大,对弹簧压缩距离起着决定性作用。分别给定电压暂降发生时刻为0.2 s和0.205 s,即暂降起始角为0°和90°。给定时间步长Ts为0.001 s,计算时长Tend为1 s。在不同的残余电压下,计算控制线圈电流和弹簧压缩距离。电压暂降起始角为90°时的计算结果如图2所示。电压暂降起始角为0°时的计算结果如图3所示。图中图例为不同残余电压幅值。

电压暂降起始角为0°时,控制线圈电流存在明显的非周期分量,残余电压越小,非周期分量越明显。假定弹簧压缩距离小于5 mm时,交流接触器跳脱,以此判断可耐受电压暂降的持续时间。当电压暂降起始角为0°、残余电压大于80%时,交流接触器未跳脱。比较弹簧压缩距离达到5 mm的时间,可以发现残余电压为70%时,所需时间最长,约为110 ms,其次是残余电压为0的情况,约为100 ms。残余电压为60%时,所需时间最短,约为20 ms。从而可验证在电压暂降起始角为0°时,由于控制线圈电流存在非周期分量,交流接触器电压暂降抗扰特性具有非单调性。另外,电压暂降造成交流接触器弹簧压缩距离变小时,由于气隙增大,磁阻增加,电感值降低,将造成控制线圈电流增大,呈现出非线性特性。因此,控制线圈电流增大可作为跳脱的判据之一。

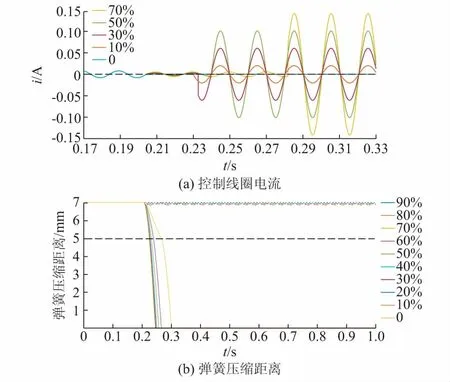
图2 电压暂降起始角为90°时的计算结果Fig.2 Calculation results with voltage sag starting angle of 90°

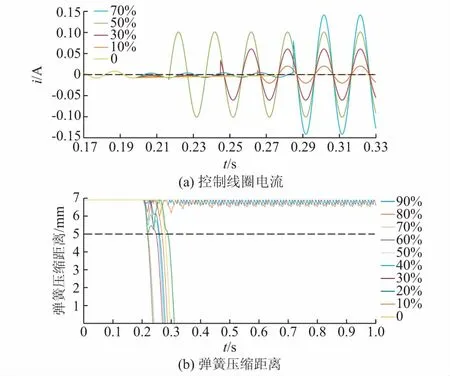
图3 电压暂降起始角为0°时的计算结果Fig.3 Calculation results with voltage sag starting angle of 0°

当电压暂降起始角为90°,残余电压大于80%时,交流接触器未跳脱。比较弹簧压缩距离达到5 mm的时间,可以发现残余电压越大,所需时间越长,从而可以验证在电压暂降起始角为90°时,由于控制线圈电流基本没有非周期分量,交流接触器电压暂降抗扰特性具有单调性。根据理论计算获得交流接触器的VTC见附录A图A3。当电压暂降起始角为0°时,抗扰特性具有非单调性,而在电压暂降起始角为90°时,抗扰特性具有单调性。

5 实验验证

本文参考国家标准[12-13]对多种类型的交流接触器进行了实验验证,其中给出ABB的A30型交流接触器的实验结果验证本文的理论分析结果。扰动源采用阿美特克公司MX系列的MX Ⅱ 45,电压输出范围为0～400 V,最大输出功率为45 kVA。对交流接触器进行测试,获得不同电压暂降起始角下交流接触器的一簇VTC见附录A图A4。电压暂降起始角为90°和270°时,电压暂降抗扰特性具有单调性,而电压暂降起始角为其他值时,电压暂降抗扰特性均具有非单调性。

采用YOKOGAWA公司的DLM2054示波器对控制线圈的电流进行观察。电压暂降起始角为90°,残余电压分别为10%和30%时,控制线圈的电压和电流波形如图4(a)和(b)所示。从实测电流波形中可以看出,当电压暂降起始角为90°时,控制线圈电流中没有非周期分量。残余电压为10%和30%时,交流接触器跳脱时间接近,但残余电压为10%时,交流接触器跳脱时间更短。当交流接触器跳脱时,控制线圈的电流会明显增加。

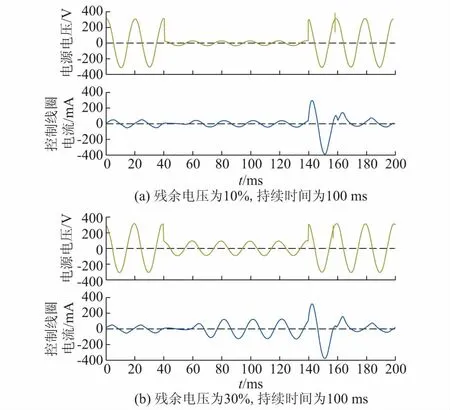
图4 电压暂降起始角为90°时控制线圈的电压和电流波形Fig.4 Voltage and current waveforms of control coil with voltage sag starting angle of 90°

电压暂降起始角为0°,残余电压分别为10%和30%时,控制线圈的电压和电流波形如图5(a)和(b)所示。从实测电流波形中可以看出,当电压暂降起始角为0°时,控制线圈电流中存在明显的非周期分量。残余电压为10%时,交流接触器跳脱时间要明显长于30%的残余电压。同样,当交流接触器跳脱时,控制线圈的电流会明显增加。实验结果与上文中的理论计算结果趋势吻合,验证了理论分析的正确性,说明了交流接触器控制线圈电流中的非周期分量是造成电压暂降非单调抗扰特性的根本原因。但实验测试结果与理论计算结果存在一定的偏差,原因是实际中交流接触器的参数较难获得,理论计算中的参数与实际参数存在一定偏差。

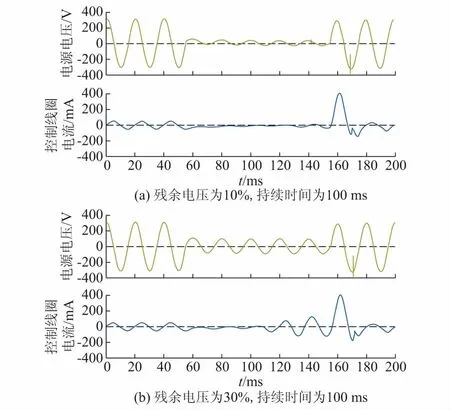
图5 电压暂降起始角为0°时控制线圈的电压和电流波形Fig.5 Voltage and current waveforms of control coil with voltage sag starting angle of 0°

6 结语

为掌握交流接触器电压暂降非单调抗扰特性的产生原因,本文通过建立交流接触器及其控制线圈的数学模型,获得了控制线圈电流与弹簧压缩距离之间的关系,并通过理论计算和实验验证,得出了电压暂降时控制线圈电流中的非周期分量是产生电压暂降非单调抗扰特性的根本原因。另外,在交流接触器跳脱时,由于气隙增大,导致控制线圈电感减小,造成控制线圈电流增大。因此,控制线圈电流变化也可作为判别交流接触器是否跳脱的条件。

但由于接触器的具体参数较难获得,且在理论分析中忽略了相位突变等因素,因此理论计算与实测结果之间存在一定的误差。交流接触器自身的差异性较大,可通过进一步增大测试样本量,获得交流接触器的电压暂降免疫度。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 鲍光海,张培铭.智能交流接触器零电流分断技术[J].电工技术学报,2012,27(5):199-204.

BAO Guanghai, ZHANG Peiming. Technology of zero-current breaking of intelligent AC contactor[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 199-204.

[2] 肖湘宁,徐永海.电能质量问题剖析[J].电网技术,2001,25(3):66-69.

XIAO Xiangning, XU Yonghai. Power quality analysis and its development[J]. Power System Technology, 2001, 25(3): 66-69.

[3] 徐永海,兰巧倩,洪旺松.交流接触器对电压暂降的敏感度研究[J].电工技术学报,2015,30(21):136-146.

XU Yonghai, LAN Qiaoqian, HONG Wangsong. Experimental research on AC contactor sensitivity during voltage sags[J]. Transactions of China Electrotechnical Society, 2015, 30(21): 136-146.

[4] 董瑶.考虑电压暂降波形起始点特征的交流接触器暂降敏感度分析[J].四川电力技术,2011,34(6):75-77.

DONG Yao. The analysis of AC contactor sensitivity considering starting point features of voltage sag waveform[J]. Sichuan Electric Power Technology, 2011, 34(6): 75-77.

[5] 赵剑锋,王浔,潘诗锋.用电设备电能质量敏感度测试系统研究[J].中国电机工程学报,2005,25(22):32-37.

ZHAO Jianfeng, WANG Xun, PAN Shifeng. Study on power quality susceptivity testing system of AC contactor[J]. Proceedings of the CSEE, 2005, 25(22): 32-37.

[7] 徐永海,洪旺松,兰巧倩.电压暂降起始点与相位跳变对交流接触器影响的分析[J].电力系统自动化,2016,40(4):92-97.DOI:10.7500/AEPS20150526001.

XU Yonghai, HONG Wangsong, LAN Qiaoqian. Influence analysis of point-on-wave of voltage sag initiation and sag phase jump on alternating current contactor[J]. Automation of Electric Power Systems, 2016, 40(4): 92-97. DOI: 10.7500/AEPS20150526001.

[8] DJOKIC S Z, MILANOVIC J V, KIRSCHEN D S. Sensitivity of AC coil contactors to voltage sags short interruptions and under voltage transients[J]. IEEE Transactions on Power Delivery, 2004, 19(3): 1299-1307.

[9] 纽春萍.陈德桂,李兴文,等.交流接触器触头弹跳的仿真及影响因素[J].电工技术学报,2007,22(10):85-90.

NIU Chunping, CHEN Degui, LI Xingwen, et al. Simulation of contact bounce of AC contactor and study of its influence factors[J]. Transactions of China Electrotechnical Society, 2007, 22(10): 85-90.

[10] 林抒毅,许志红.交流接触器三维动态过程数值计算与分析[J].中国电机工程学报,2014,34(18):2967-2975.

LIN Shuyi, XU Zhihong. Simulations and numerical analysis on 3D dynamic process of alternating current contactors[J]. Proceedings of the CSEE, 2014, 34(18): 2967-2975.

[11] 杨怡君,苏秀苹,岳大为,等.交流接触器动态响应不确定性的评价方法[J].中国电机工程学报,2013,33(33):130-138.

YANG Yijun, SU Xiuping, YUE Dawei, et al. Research on dynamic response uncertainty evaluation of AC contactors[J]. Proceedings of the CSEE, 2013, 33(33): 130-138.

[12] 电磁兼容试验和测量技术电压暂降、短时中断和电压变化的抗扰度试验:GB/T 17626.11—2008[S].2008.

[13] 电磁兼容试验和测量技术主电源每相电流大于16 A的设备的电压暂降、短时中断和电压变化抗扰度试验:GB/T 17626.34—2012[S].2012.

钟 庆(1978—),男,通信作者,博士,教授,博士生导师,主要研究方向:电力系统及其自动化、电能质量分析与控制。E-mail： epqzhong@scut.edu.cn

吴浩波(1994—),男,硕士研究生,主要研究方向:电能质量分析与控制。E-mail: 344061311@qq.com

贺 哲(1991—),男,硕士研究生,主要研究方向:电能质量分析与控制。E-mail: 498315041@qq.com