奇异值分解方法在日负荷曲线降维聚类分析中的应用
2018-02-27史俊祎商佳宜孙维真
陈 烨, 吴 浩, 史俊祎, 商佳宜, 孙维真
(1. 浙江大学电气工程学院, 浙江省杭州市 310027; 2. 国网浙江省电力公司杭州供电公司, 浙江省杭州市 310011; 3. 国网浙江省电力公司电力调度控制中心, 浙江省杭州市 310007)
0 引言
近年来,随着智能电表在电力系统中的广泛应用,电力公司积累了海量的负荷用电历史数据[1]。利用负荷曲线聚类算法从海量负荷数据中挖掘用电信息,分析用户用电行为,能够为电网规划、用电客户精细分类和制定用电计划等应用提供有力支撑[2-4]。因此,研究适用于负荷曲线的聚类算法及相关技术具有重要的应用价值。
负荷曲线聚类算法大致可分为直接聚类和间接聚类[5]。直接聚类方法通常选择负荷曲线上每个采集点的负荷数据进行聚类,包括K-means[6]、模糊C均值[7-8]、自组织神经网络[9]等。然而随着负荷数据规模不断增长,这种方法面临着计算效率的挑战。因此,有必要对负荷数据进行降维处理,以提升聚类效率。
间接聚类方法通过提取负荷曲线的特征作为降维指标,以此为输入进行聚类。文献[10]利用主成分分析方法提取出少量主成分作为降维指标,并采用K-means算法进行聚类。文献[11]选取了6种反映用户负荷特征的日负荷特性指标进行聚类。文献[12]利用Sammon映射将原始负荷曲线映射到低维空间中,然后利用低维空间中的映射值进行聚类。文献[13]认为低维负荷数据经深度学习反馈后可用来反映原始负荷数据。文献[14]采用离散傅里叶变换在频域中提取负荷特征作为降维指标,对负荷曲线进行分类。
上述间接聚类方法选择了不同的降维指标对负荷曲线进行聚类,但在降维处理过程中均面临两个问题:降维指标数目的确定和降维指标权重的确定。降维指标的数目是负荷曲线降维处理后的维度,合适的指标数目不仅能够提高聚类的准确性,而且能提升聚类效率,故应客观论证所选取的降维指标数目是否已为最优[15]。此外,由于各降维指标的侧重角度不同,使得在反映用户用电特性时其重要程度也不同,因此有必要对各指标赋予相应的权重。这两个问题的解决有助于提升间接聚类方法聚类结果的准确性和效率。
奇异值分解(singular value decomposition,SVD)是一种常用的数学方法,已在多个领域得到应用。例如,在电力系统领域,潮流雅可比矩阵的最小奇异值被用于评估电压稳定能力[16],SVD还可用于故障诊断和状态估计[17]等。在图像处理领域,SVD可用于去除图像中的噪声,尽可能地保留原图像的数据特征[18]。同理,若将负荷曲线数据视作图像,采用SVD提取出主要的数据特征,再利用这些数据特征对负荷曲线进行降维聚类。
在上述背景下,本文提出了一种基于SVD的日负荷曲线降维聚类方法,较好地解决了上述两个问题。利用SVD将负荷曲线数据旋转变换至新的坐标系,以负荷曲线在各坐标轴上的坐标为降维指标,确定降维指标的数目后,选择奇异值为指标权重。算例表明该算法运行时间短,能够提供合理的用户分类。
1 聚类算法的基本理论
1.1 SVD的基本思想
SVD是一种常用的数据变换方法[19],现以二维数据为例,解释SVD的数学思想。
如附录A图A1所示,3类由不同颜色构成的二维数据绘制在由坐标轴x1-x2构成的直角坐标系内。数据在2个坐标轴上的分布较离散,难以判断哪个坐标轴更为重要,且在2个坐标轴上的投影重叠,会影响数据聚类的准确性。由于数据所含的信息可用其方差来表征,方差越大,该数据离散程度越大,所包含的信息越多。现对坐标系作旋转变换,以数据变化方差最大的方向为轴,得到一个新的正交坐标系v1-v2。此时,数据主要沿着v1轴变化,而在v2轴上分布得较为集中。若忽略在v2轴上的微小偏差量,仅将数据投影在v1轴上,这样就将原来的二维数据在保留大部分信息的前提下简化成一维数据。然后,利用数据在v1轴上的坐标值进行聚类,在降低数据维度的同时也保证了聚类的准确性。
一般的,该思想可扩展至n维数据。假设存在m条负荷曲线,每条负荷曲线有n个采样点,可将这m条负荷曲线视为n维坐标系x1-xn下的m个数据点。同理,直接利用数据点在变换后低维坐标系下的坐标值进行聚类,可达到降维聚类的目的。
值得注意的是,SVD的基本思想与主成分法有一定的相似性,但较主成分法而言,SVD的优势主要体现在以下两个方面。
1)初始化处理。由于主成分法需对原始数据作零均值化处理,这会消去平稳负荷曲线的重要特征。
2)计算稳定性。主成分法由于需要计算协方差矩阵的特征向量,增加了计算复杂度并会产生舍入误差,而SVD不需要进行这一步骤,具有较强的计算稳定性,能够简单、直观地展示数据旋转变换的过程[20]。
1.2 SVD的数学理论
为了更好地理解SVD应用于日负荷曲线聚类的过程,本文直接以负荷曲线为例阐述SVD的数学理论。设有一个由m条负荷曲线构成的m×n阶实矩阵A=[a1,a2,…,am]T,其中负荷曲线ak=[ak,1,ak,2,…,ak,n]T有n个采样点。在SVD理论中[19],对于矩阵A,存在正交矩阵U∈Rm×m和V∈Rn×n,使得
(1)
式中:正交矩阵U=[u1,u2,…,um]的列向量为单位向量且相互正交,同时是矩阵AAT的特征向量,称为左奇异向量;正交矩阵V=[v1,v2,…,vn]的列向量也为单位向量且相互正交,同时是矩阵ATA的特征向量,称为右奇异向量;Λ1=diag(λ1,λ2,…,λp),其中p=min(m,n)。Λ1是对角矩阵,其对角元素为矩阵A的奇异值并按降序排列,即λ1≥λ2≥…≥λp。由于m通常大于n,因此在本文中令p=n。值得指出的是,m小于n时,本文方法依然适用。式(1)可展开为:
A=UΛVT=
(2)
以矩阵A中某条负荷曲线ak为例,由式(2)可推导出:
ak=[λ1u1,kλ2u2,k…λnun,k]·
(3)
式中:u1,k为向量u1在第1点的坐标,u2,k等同理。
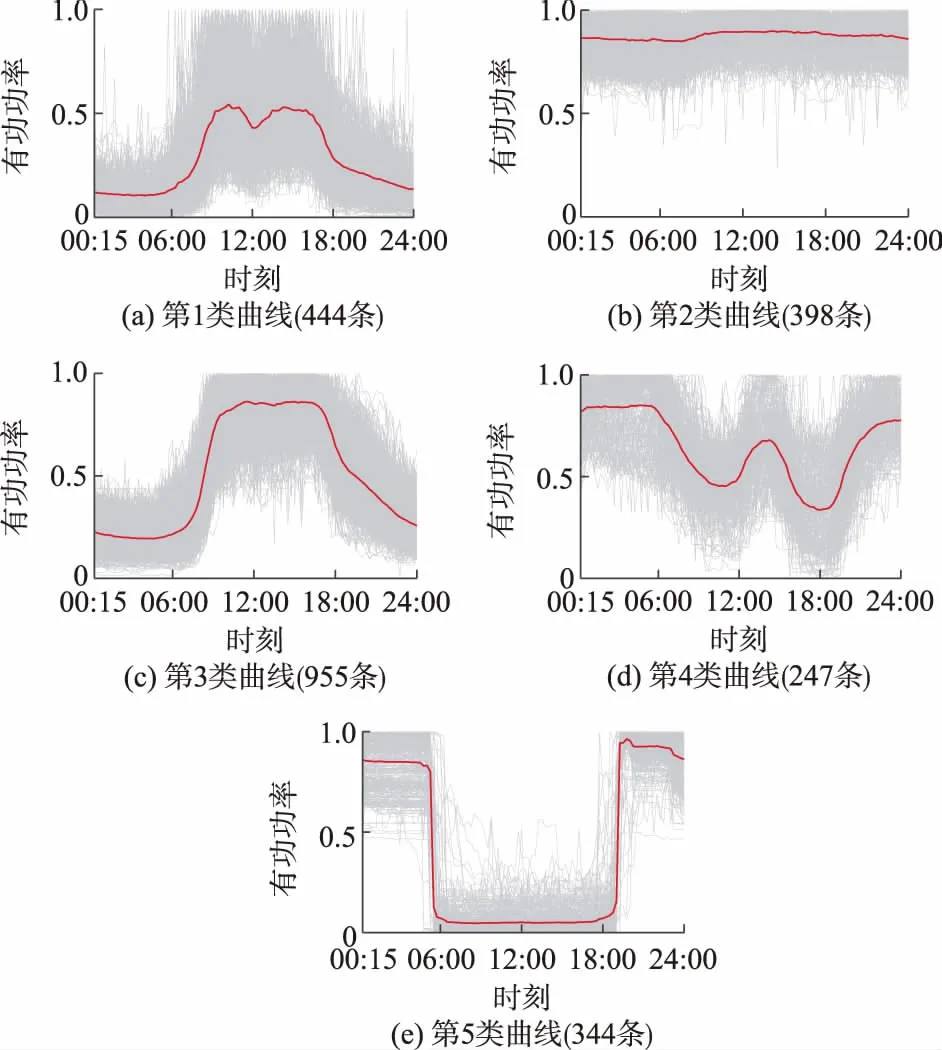
SVD理论中[20],以向量v1,v2,…,vn为坐标轴的方向向量构建了新正交坐标系,奇异值λi为从向量ui到坐标轴vi进行缩放的比例,λiui,k即为负荷曲线ak在坐标轴vi上的坐标值。此外,由于奇异值λi越大,导致缩放的比例越大,使得坐标值在坐标轴vi上的离散程度越大,这样坐标轴vi反映的数据方差越大,该坐标轴也越重要,因此,可认为较小奇异值对应的部分代表了能够忽略的噪声[20]。这样,由式(2)和式(3),仅保留前q(q (4) ak=[λ1u1,kλ2u2,k…λquq,k]· (5) 由式(4)和式(5)可知,在忽略掉数据变化方差较小的方向后,将坐标系v1,v2,…,vn简化为低维坐标系v1,v2,…,vq。这样,负荷曲线ak在低维坐标系中的坐标值λiui,k可用来反映负荷曲线的主要特征。 负荷曲线数据经SVD变换至新的低维坐标系后,可获得在各坐标轴上的坐标,进而反映出负荷曲线在各方向上的特征,坐标越接近的负荷曲线越相似。因此,可将负荷曲线ak在前q个坐标轴上的坐标作为降维指标,设为Yk=[yk,1,yk,2,…,yk,q]=[λ1u1,k,λ2u2,k,…,λquq,k]。这样,对于每条负荷曲线,用于聚类的数据从n个减少为q个。令集合Y={Y1,Y2,…,Ym}包含所有负荷曲线的降维指标值。 此外,各坐标轴对应的奇异值描述了该方向的重要程度,在利用坐标值聚类时,奇异值越大,对应方向上的坐标值越重要。故选择坐标轴对应的奇异值作为降维指标的权重,再对其作总和为1的归一化处理,记为权重向量W,W=[w1,w2,…,wq]。 2.1.1异常数据的识别与修正 在负荷数据采集过程中,可能会发生测量装置故障、数据传输中断等问题,导致负荷数据异常。当某条负荷曲线的数据缺失量和异常量超过10%或以上时,认为该曲线无效。 设xk=[xk,1,xk,2,…,xk,n]T为从量测装置中收集的某条原始负荷曲线,对数据的异常状态识别可通过负荷变化率进行判断: (6) 式中:δk,i为负荷曲线在第i点的负荷变化率,当其超过预设阈值ε后视为异常数据,通常ε可取0.5~0.8。对于此类异常数据点可利用平滑修正公式进行修正: (7) 2.1.2负荷曲线归一化 由于原始负荷数据值之间可能会存在巨大差异,不经处理的聚类会影响聚类效果,使得聚类结果不可靠。对此,采用极大值归一化方法对负荷数据进行归一化,表达式如下: (8) 式中:ak,i为在采样点i归一化后的数据。这样,经数据预处理后的负荷曲线ak构成了矩阵A。 由第1节中降维指标的定义可知,数值q即为降维指标的数目。由于奇异值按降序排列,通过充分利用奇异值下降趋势的信息来确定q值。具体的,结合最小二乘法使直线y=ax+b对奇异值下降段拟合的平均误差最小,此时拟合所用的数据点数即为q值。具体步骤如下。 步骤1:计算奇异值。对矩阵A作奇异值分解,并记录n个数据点(i,λi)为数据集S。 步骤3:计算拟合误差。按式(9)计算选择q个数据点时拟合的平均误差Γq,并记入数据集Γ中。 (9) 步骤4:令q=q+1,当q>n或拟合误差已连续增长5次(误差具有明显增长趋势)时,转到步骤5,否则转到步骤2。 步骤5:找到集合Γ中的最小值,其对应的q值即为最终选定的降维指标的数目。 这样,在确定降维指标的数目q后,依据1.3节的定义,计算出降维指标集Y和权重W。 基于加权欧式距离的K-means算法,是以降维指标集Y为输入,加权欧式距离为相似性判据进行聚类,加权K-means算法的处理步骤如下。 步骤1:初始化。设k为聚类数,在集合Y中随机选择k个样本,作为初始聚类中心。 步骤2:样本归类。将所有样本划分到其加权欧式距离最近的类中心,从样本Yk到第j个聚类中心mj=[mj,1,mj,2,…,mj,q]的加权距离可由下式计算: d(k,j)= (10) 步骤3:聚类中心更新。根据步骤2的结果,计算每类的平均值作为各类新的聚类中心。 步骤4:迭代计算。判断聚类中心是否收敛,若未收敛则跳转至步骤2,否则算法结束。 聚类有效性检验是通过建立有效性指标,评价聚类结果并确定最佳聚类数的过程。Silhouette指标是现有聚类方法中常用的有效性指标之一[11,21],可用于确定最佳聚类数并评价聚类质量。 设负荷曲线被划分为k类,对于第j类中第i个样本,计算样本i的Silhouette指标ΩSil(i),定义如下: (11) 式中:da(i)为样本i到非同类所有样本的最小平均距离,用以反映类间距离大小;db(i)为样本i与类内其余样本的平均距离,用以反映类内紧凑程度。当da(i)越大,db(i)越小,样本i所属类j的类内紧凑程度和类间距离越好,聚类结果越优。 所有负荷曲线的Silhouette指标均值ΩSilM可用于评价总体聚类质量,其值越大表示聚类质量越优,并确定ΩSilM最大值对应的类数k为最佳聚类数。ΩSilM的计算表达式如下: (12) 本文选取中国某市2015年8月某工作日实测2 413个用户的日负荷曲线为研究对象,日负荷采样间隔为15 min,每日共计96个采样点。以附录A图A2为例,简要说明数据预处理过程,其中预设阈值ε取0.5,p1和q1均取为3。由附录A图A2可得,经数据预处理后,对负荷曲线上的数据异常点进行了修正,最终算例共含2 388条有效日负荷曲线,构成2 388×96阶矩阵A。本文以典型日负荷曲线为例,验证所提方法能否提高负荷曲线聚类的准确性和效率。 对矩阵A作奇异值分解后绘制奇异值曲线,如附录A图A3所示,放大图中绘制了前15个奇异值,蓝色虚线为q=3时的拟合直线y=ax+b。然后,计算得到拟合误差数据集Γ如附录A表A1所示。 由附录A表A1可知,当降维维度q=3时,有最小的拟合误差,故确定本算例的降维指标数目为3。由此将2 388条日负荷曲线在前3个坐标轴上的坐标值作为降维指标值,得到2 388×3阶降维指标Y,同时3个降维指标对应的权重向量为W=[0.61,0.286,0.104]。采用加权K-means算法对Y聚类,将聚类结果与直接以96个采样点的数据为输入,经极大值归一化后直接利用K-means算法聚类(以下改称传统聚类算法)的结果作对比。 由附录A图A4聚类有效性指标检验结果可知,当聚类数为5时,2种算法指标均值ΩSilM最大,因此确定最佳聚类数均为5。在图1和附录A图A5中,红色线为该类负荷曲线的平均值,通常认为其是该类负荷的典型负荷曲线。本文聚类算法聚类结果中属于各类的曲线数目依次为444,398,955,247和344,传统聚类算法聚类结果中属于各类的曲线数目依次为459,399,939,249和342,其分类数目和分类结果基本一致。 图1 基于本文聚类算法的日负荷曲线聚类结果Fig.1 Load profiles clustering results of proposed clustering method 图2所示为2种算法提取的5类典型负荷曲线,具有相似的负荷形态,均呈双峰、峰平期、单峰、错峰和避峰5种类型。双峰型曲线多为小工业用户,工作时间固定且规律;峰平期型曲线主要包括大工业等;单峰型曲线主要为正常的商业用电,白天工作量大,晚间休息;错峰型负荷多为农业用电,在晚间打光灭虫、排涝和灌溉等;避峰型负荷较为特殊,主要是公用路灯等。因此,从工程角度来看,本文聚类算法分类结果合理,具有实际应用价值。 由表1可见,通过聚类有效性指标和程序运行时间综合比较2种算法的性能。在最佳聚类数均为5的情况下,使用本文聚类算法进行聚类的运行时间仅为传统聚类算法聚类结果的1/5左右,同时前者的指标均值ΩSilM稍大于后者,其聚类质量略占优势。这主要是因为基于SVD降维时能够忽略原始数据中噪声的干扰,使得提取主要数据特征后的降维聚类更加有效。综上,本文所提降维聚类算法能够较为准确地对日负荷曲线进行分类,并缩减了程序运行时间。 图2 两种算法提取的典型负荷曲线对比Fig.2 Comparison of typical load profiles between two methods 算法最佳聚类数指标均值ΩSilM程序运行时间/s数据降维主程序合计本文聚类算法50.5391.5945.0786.672传统聚类算法50.53532.64132.641 降维指标的数目对于聚类结果有重要影响,上节算例中该数目为3,进一步验证数目的增加能否提高聚类效果,数目的减少能否在保证聚类准确性的前提下提高计算速度等。 附录B表B1列出了不同的降维指标数目下,指标均值ΩSilM的大小和聚类运行的时间。当降维指标的数目减小至2时,由于忽略了方差第三大的坐标轴,虽然最佳分类数仍为5,但指标均值ΩSilM偏小;当数目增加至4和5时,分类结果保持不变,但计算时间分别增加了5.38%和10.98%。因此,由本文所提方法确定的降维指标数目作聚类时,在保证聚类结果良好的同时,提高了计算效率。 附录A图A3中,奇异值下降的趋势用以判断降维指标的数目。经研究发现,当仅使用少量数目的负荷曲线时,计算得到的奇异值下降趋势与使用所有负荷曲线的趋势相似。 如图3所示,随机选择100,500和1 000条负荷曲线并分别执行50次,相应的奇异值分别绘制在图3(a)(b)(c)中,作为对比,附录A图A3中的原始奇异值绘制在图3(d)中。对于图3(a)(b)(c)而言,在分别执行50次后,每一编号下的奇异值均匀分布在一个稳定的范围中,对应的奇异值下降趋势与图3(d)中十分相似,经验证发现最终获得的降维指标数目也相同。 图3 不同负荷曲线数目下的奇异值Fig.3 Singular values under different numbers of load profiles 因此,仅利用少量的负荷曲线即可确定降维指标数目。这样,本文聚类算法中用于数据降维的时间将进一步减少。 以含噪声的模拟日负荷曲线为例,在已知其正确聚类结果的基础上,验证所提聚类算法的耐噪声能力及鲁棒性。基于8类典型日负荷曲线(见附录C图C2红色线),分别在每类典型曲线的每个数据点上添加比例为r的随机噪声,进而模拟得到分属8类、每类125条总计1 000条的日负荷曲线,以此构成矩阵A。这8类典型曲线中,第1类与第2类为双峰型,多为政府等机构用户,但两类负荷曲线的幅值存在差异,增加了准确分类的难度;第3类与第6类白天用电量稍低,晚上工作量大,两者幅值和形状略有不同;第4类为峰平期型,包括大工业用户等;第5类和第7类为单峰型,多为正常的商业用电;第8类为错峰型,多为公用事业和农业用电等。因此,从工程角度来看,选取的8类负荷曲线具有一定的典型负荷用电特征。 在改变噪声比例r后,采用本文聚类算法和传统聚类算法对模拟负荷曲线进行聚类,并定义分类准确率为1 000条负荷曲线中得到准确分类的负荷曲线所占百分比。因此,算法的鲁棒性可以通过最佳聚类数、指标均值ΩSilM和分类准确率3种指标进行检验,结果如表2所示。 表2 两种算法鲁棒性比较Table 2 Comparison of robustness between two methods 从表2可得出以下结论。 1)对于两种聚类算法,随着噪声比例不断增加,指标均值ΩSilM和分类准确率下降,最佳聚类数出现偏差,表明3种指标可以用来检验算法的鲁棒性。 2)当噪声比例不超过20%时,两种聚类算法的分类准确率均近似100%。 3)当增大噪声比例至不超过30%时,本文聚类算法的最佳聚类数一直为8,分类准确率近100%,而传统聚类算法在噪声比例增大至30%后,最佳聚类数不再为8,分类准确率下降,鲁棒性较差。 4)当继续增大噪声比例至不超过40%时,两种聚类算法的最佳聚类数均不为8,但本文聚类算法的分类准确率和指标均值均稍优于传统聚类算法。 以噪声比例r=30%为例,1 000条模拟负荷曲线原始分类如附录C图C1所示。将基于本文聚类算法提取的8类典型负荷曲线与初始典型负荷曲线进行对比,如附录C图C2所示。为了量度两组负荷曲线的拟合程度,定义误差指标Eerr: (13) 由附录C图C2和附录C表C1可见,两组负荷曲线形态高度相似,拟合误差较小。综上,所提方法对典型日负荷曲线提取效果良好,较为准确地还原了初始典型日负荷曲线的特征,耐噪声能力强。 本文提出了一种基于SVD的日负荷曲线降维聚类方法。通过SVD降维和选取加权欧式距离作为相似性判据,对日负荷曲线进行聚类。此聚类方法能够解决传统间接聚类方法的两大问题。 1)降维指标数目的不确定性。本文充分利用了奇异值下降趋势,基于最小二乘法确定降维指标的数目。 2)降维指标权重的不确定性。奇异值大小描述了降维指标包含信息的程度,以此为权重作加权聚类。 算例表明该方法具有良好的划分能力,且大幅缩减了程序运行时间。随着大数据时代的到来,如何结合环境等多影响因素,构建更为精细化的聚类方法是今后的研究方向。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 [1] AGHAEI J, ALIZADEH M I. Demand response in smart electricity grids equipped with renewable energy sources: a review[J]. Renewable & Sustainable Energy Reviews, 2013, 18(2): 64-72. [2] WANG Y, CHEN Q, KANG C, et al. Clustering of electricity consumption behavior dynamics toward big data applications[J]. IEEE Transactions on Smart Grid, 2016, 7(5): 2437-2447. [3] 林济铿,刘露,张闻博,等.基于随机模糊聚类的负荷建模与参数辨识[J].电力系统自动化,2013,37(14):50-58. LIN Jikeng, LIU Lu, ZHANG Wenbo, et al. Load modeling and parameter identification based on random fuzziness clustering[J]. Automation of Electric Power Systems, 2013, 37(14): 50-58. [4] 鞠平,金艳,吴峰,等.综合负荷特性的分类综合方法及其应用[J].电力系统自动化,2004,28(1):64-68. JU Ping, JIN Yan, WU Feng, et al. Studies on classification and synthesis of composite dynamic loads[J]. Automation of Electric Power Systems, 2004, 28(1): 64-68. [5] 朱文俊,王毅,罗敏,等.面向海量用户用电特性感知的分布式聚类算法[J].电力系统自动化,2016,40(12):21-27.DOI:10.7500/AEPS20160316007. ZHU Wenjun, WANG Yi, LUO Min, et al. Distribution clustering algorithm for awareness of electricity consumption characteristics of massive customers[J]. Automation of Electric Power Systems, 2016, 40(12): 21-27. DOI: 10.7500/AEPS20160316007. [6] 刘思,傅旭华,叶承晋,等.考虑地域差异的配电网空间负荷聚类及一体化预测方法[J].电力系统自动化,2017,41(3):70-75.DOI:10.7500/AEPS20160507003. LIU Si, FU Xuhua, YE Chengjin, et al. Spatial load clustering and integrated forecasting method of distribution network considering regional difference[J]. Automation of Electric Power Systems, 2017, 41(3): 70-75. DOI: 10.7500/AEPS20160507003. [7] 曾博,张建华,丁蓝,等.改进自适应模糊C均值算法在负荷特性分类的应用[J].电力系统自动化,2011,35(12):42-46. ZENG Bo, ZHANG Jianhua, DING Lan, et al. An improved adaptive fuzzy C-means algorithm for load characteristics classification[J]. Automation of Electric Power Systems, 2011, 35(12): 42-46. [8] 孔祥玉,胡启安,董旭柱,等.引入改进模糊C均值聚类的负荷数据辨识及修复方法[J].电力系统自动化,2017,41(9):90-95.DOI:10.7500/AEPS20160920002. KONG Xiangyu, HU Qi’an, DONG Xuzhu, et al. Load data identification and correction method with improved fuzzy C-means clustering algorithm[J]. Automation of Electric Power Systems, 2017, 41(9): 90-95. DOI: 10.7500/AEPS20160920002. [9] 李智勇,吴晶莹,吴为麟,等.基于自组织映射神经网络的电力负荷曲线聚类[J].电力系统自动化,2008,32(15):66-71. LI Zhiyong, WU Jingying, WU Weilin, et al. Power customers load profile clustering using SOM neural network[J]. Automation of Electric Power Systems, 2008, 32(15): 66-71. [10] KOIVISTO M, HEINE P, MELLIN I, et al. Clustering of connection points and load modeling in distribution systems[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1255-1265. [11] 刘思,李林芝,吴浩,等.基于特性指标降维的日负荷曲线聚类分析[J].电网技术,2016,40(3):797-803. LIU Si, LI Linzhi, WU Hao, et al. Cluster analysis of daily load curves using load pattern indexes to reduce dimensions[J]. Power System Technology, 2016, 40(3): 797-803. [12] 张斌,庄池杰,胡军,等.结合降维技术的电力负荷曲线集成聚类算法[J].中国电机工程学报,2015,35(15):3741-3749. ZHANG Bin, ZHUANG Chijie, HU Jun, et al. Ensemble clustering algorithm combined with dimension reduction techniques for power load profiles[J]. Proceedings of the CSEE, 2015, 35(15): 3741-3749. [13] VARGA E D, BERETKA S F, NOCE C, et al. Robust real-time load profile encoding and classification framework for efficient power systems operation[J]. IEEE Transactions on Power Systems, 2015, 30(4): 1897-1904. [14] ZHONG S, TAM K S. Hierarchical classification of load profiles based on their characteristic attributes in frequency domain[J]. IEEE Transactions on Power Systems, 2015, 30(5): 2434-2441. [15] 陆俊,朱炎平,彭文昊,等.智能用电用户行为分析特征优选策略[J].电力系统自动化,2017,41(5):58-63.DOI:10.7500/AEPS20160607002. LU Jun, ZHU Yanping, PENG Wenhao, et al. Feature selection strategy for electricity consumption behavior analysis in smart grid[J]. Automation of Electric Power Systems, 2017, 41(5): 58-63. DOI: 10.7500/AEPS20160607002. [16] 徐志友,栾兆文,樊涛,等.衡量节点稳定的奇异值和稳定指标[J].电力系统自动化,1997,21(8):42-44. XU Zhiyou, LUAN Zhaowen, FAN Tao, et al. The singular value method for estimating node voltage stability and stability index[J]. Automation of Electric Power Systems, 1997, 21(8): 42-44. [17] 王韶,江卓翰.基于奇异值分解和等效量测变换的电力系统状态估计[J].电力系统保护与控制,2012,40(12):111-115. WANG Shao, JIANG Zhuohan. Power system state estimation based on singular value decomposition and equivalent current measurement transformation[J]. Power Systems Protection and Control, 2012, 40(12): 111-115. [18] 刘涵,梁莉莉,黄令帅.基于分块奇异值分解的两级图像去噪算法[J].自动化学报,2015,41(2):439-444. LIU Han, LIANG Lili, HUANG Lingshuai. Two-stage image denoising using patch-based singular value decomposition[J]. Acta Automatica Sinica, 2015, 41(2): 439-444. [19] HAYES M H. Properties of the singular value decomposition for efficient data clustering[J]. IEEE Signal Processing Letters, 2004, 11(11): 862-866. [20] GOLUB G, LOAN C. Matrix computation[M]. Baltimore, USA: Johns Hopkins University Press, 1996. [21] AlOTAIBI R, JIN N, WILCOX T, et al. Feature construction and calibration for clustering daily load curves from smart-meter data[J]. IEEE Transactions on Industrial Informatics, 2016, 12(2): 645-654. 陈 烨(1994—),男,硕士研究生,主要研究方向:电力系统仿真分析与建模。E-mail: chenye19941002@163.com 吴 浩(1973—),男,通信作者,博士,副教授,主要研究方向:电力系统运行优化、电力系统稳定、负荷建模等。E-mail: zjuwuhao@zju.edu.cn 史俊祎(1993—),女,硕士研究生,主要研究方向:负荷聚类及其在电力市场的应用。E-mail: sjyi@zju.edu.cn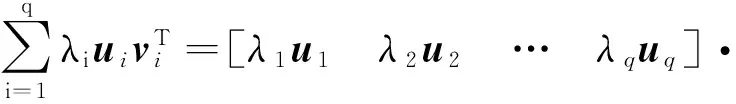

1.3 降维指标及其权重
2 基于奇异值分解的聚类算法
2.1 数据预处理
2.2 确定降维指标的数目
2.3 加权K-means聚类

2.4 聚类有效性检验
3 算例分析
3.1 实际日负荷曲线聚类
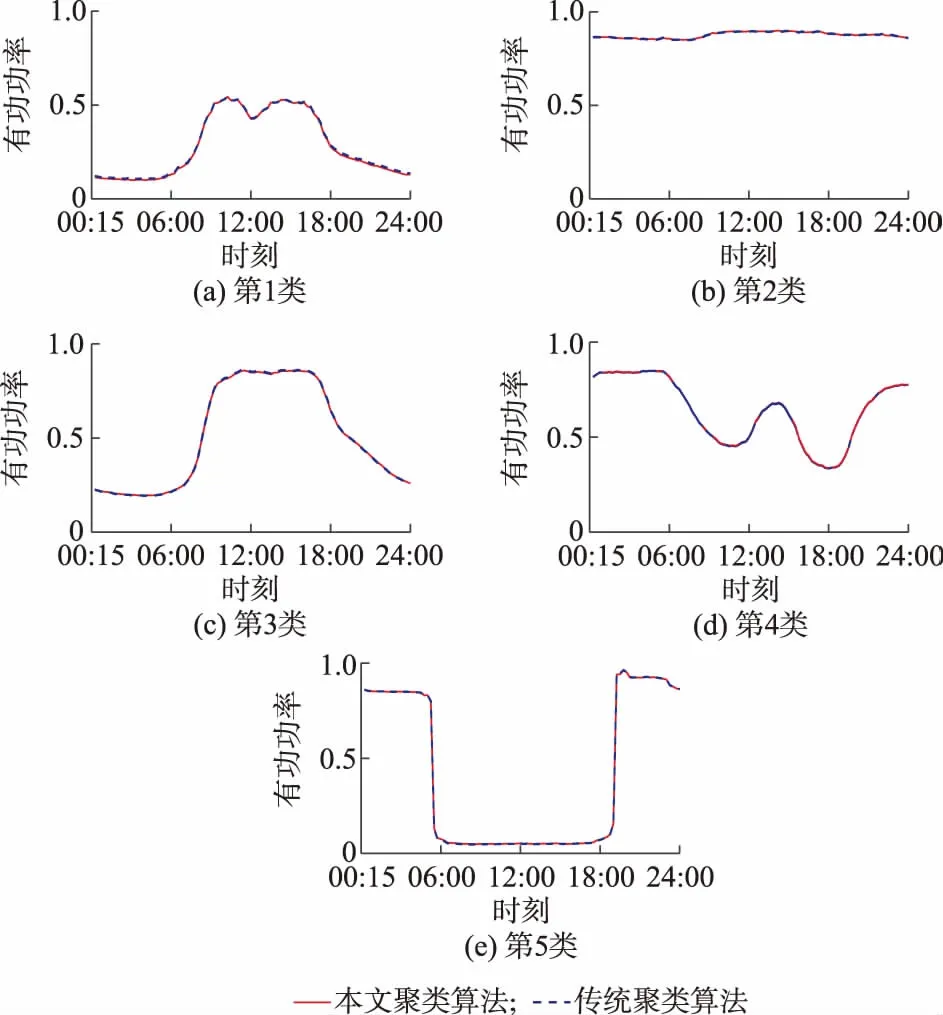
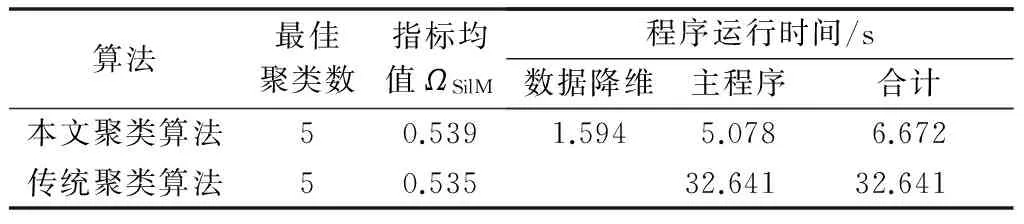
3.2 降维指标数目的验证
3.3 奇异值下降趋势相似性的验证
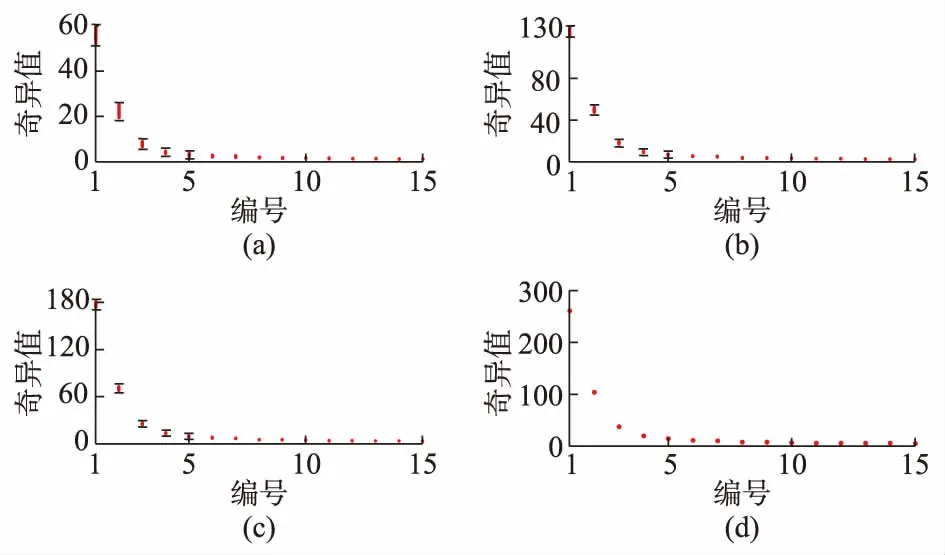
3.4 模拟日负荷曲线聚类
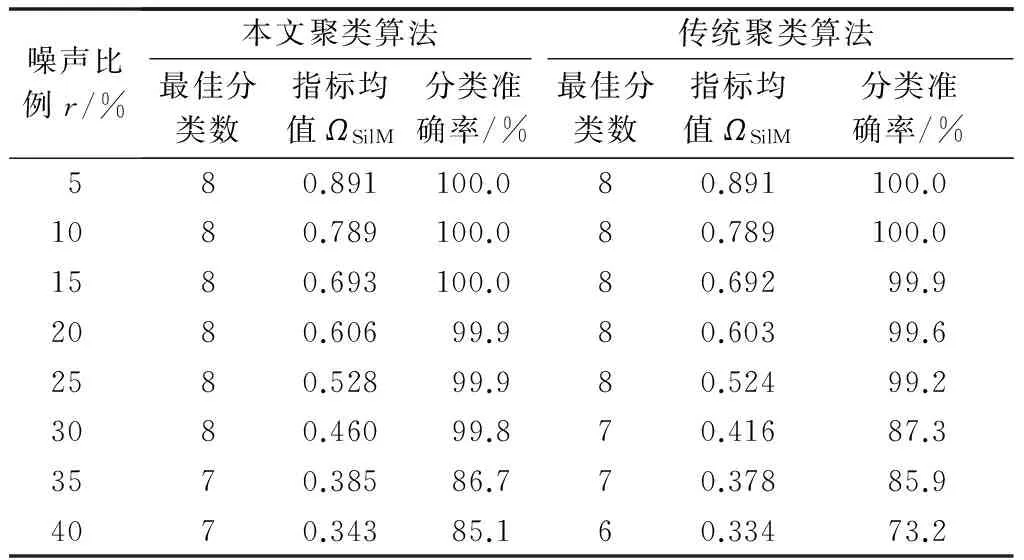
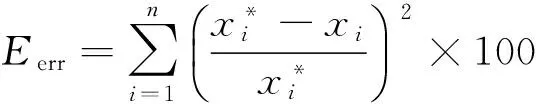
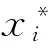
4 结语
