考虑用户行车习惯的电动汽车充电双层控制策略

何 西, 涂春鸣, 王丽丽, 李 珺, 李昭颖

(1. 国家电能变换与控制工程技术研究中心(湖南大学), 湖南省长沙市 410082; 2. 深圳市龙岗出入境检验检疫局, 广东省深圳市 518100)

0 引言

电动汽车作为解决全球能源危机以及环境污染的重要手段,受到越来越多的关注。各国政府也通过制定各种政策加速电动汽车的普及[1]。中国电动汽车也得到迅速发展[2]。

从电网角度来看,大量电动汽车的接入将对电网的稳定带来很大的挑战,如造成电网线路阻塞,节点电压降低,加速变压器老化等问题[3]。考虑到电动汽车大部分时间(90%)都处于停放状态,其充电时间远小于停放时间,可考虑将其看成可控负荷进行类需求侧管理[4]。欧洲一些电动汽车普及率较高的国家率先提出了智慧充电(smart charge)的概念,以取代传统随到随充、以固定功率充电的模式。还有学者提出将电动汽车作为储能元件向电网反送能量的电动汽车入网(V2G)模式,以减小电网频率及电压波动[5]。然而,对于智慧充电应如何实现充电功率的控制,以及充电控制策略和控制算法的选取等诸多问题还一直处于研究摸索阶段。

在充电控制策略方面,大致可分为集中控制和分散控制2类。集中控制是一种由上而下的单向控制,控制单元根据负荷属性以及当前电网负荷状态对设备进行选择性切断,类似于需求侧管理,其目的是削减高峰负荷。由于是单向控制,用户信息无法传输至控制中心,导致用户充电需求得不到充分满足。分散控制以电网节点为单位将电动汽车划分成多个集合进行控制,其优点是通信需求小,隐私性和自治性可得到满足;缺点是由于本地自治,各集合根据自身充电利益最大化进行充电控制,缺少各个集合之间的协调沟通,加剧电网阻塞。文献中比较常见的分时电价法可以看成是一种集中控制策略[6]。文献[7]提出将电动汽车集群看成可控负荷进行需求侧管理,提出一种三步式控制策略。文献[8]基于欧洲“SMART V2G”项目,提出了集中式需求侧管理算法。文献[9]以葡萄牙一个典型的400 V低压配电网为对象,验证了在不对电网进行扩容的情况下,智慧充电模式可以消纳的电动汽车占比为61%,远高于常规充电模式下的11%。但上述文献仅仅阐述了策略的框架,并未提出具体的实现步骤和目标函数。

在控制算法方面,文献[10]利用拉格朗日松弛法把集中控制问题分解成多个停车场的分散控制问题,并用一种有效的启发式算法快速收敛得到合适解。文献[11]提出了利用纳什均衡原理将充电负荷转移到用电低谷。通过仿真发现,如果所有电动汽车同质(所有汽车具有相同电池参数),算法将全局收敛或基本全局收敛于平衡点。但是这种纯数学的公式推导在实际中的应用价值有待商榷。

对于含大量电动汽车接入的电网,综合考虑2种控制模式的优缺点,并结合中国电网的垂直结构以及独特的管理模式,提出一种分层的智能充电模式。即将充电控制优化成2个阶段,在不同的阶段应用不同的控制策略。分层控制策略分为以下3个步骤。

1)通过MATSim软件对用户行车模式进行模拟,并根据用户充电习惯进行集合归类。

2)集中控制器以总体成本、尖峰负荷、负荷平滑度为目标函数,对全部用户群进行全局优化,并对各个集合的功率和能量进行指导(集中控制)。

3)依据2)中所得到的结果,对各个集合内个体使用交替方向乘子法(ADMM)进行优化,使个体充电费用最低且满足自身充电需求(分散控制)。

1 用户行车行为模式分析

充电策略的确定不仅与电池特性、充电基础设施有关,还与用户的行车习惯有很大的关系,例如出发、到达时间、行程中的能耗、停车地点等。用户行车行为模式可以通过数据统计和软件模拟获得。数据统计根据各个地区交通部门统计的个体出行数据得到用户行车模式,例如美国联邦交通部每年发布的《National Household Travel Survey》报告[12]。数据统计法的最大缺点是统计数据主要是以传统汽车为样本进行统计,并没有考虑电动汽车行车模式的特殊性,例如其相对较短的续航里程,充电桩分布带来的活动范围限制,群体素质带来的活动范围及行车路线的差异,充电地点和充电习惯,混合动力汽车与纯电动汽车比例等。本文采用MATSim软件来模拟电动汽车用户行车行为模式。

MATSim是一款基于代理机制进行交通路线优化、用户行车模式分析、路网负荷模拟的开源软件,用户可以根据任务的具体特点加载模块,从而进行二次开发[13]。MATSim仿真流程由初步需求、执行、打分、结果分析、策略调整5个步骤构成。初步需求包含每个代理1 d中的计划(Plan),该计划包含一系列状态(例如在家还是上班)、起点和终点、时间点(例如08:00 离家,18:00 下班),以及其他一些额外的信息(例如每千米耗电量)。代理中的汽车根据初步需求中制定的计划执行。当一次执行结束之后,系统根据协同进化算法对每一次执行情况进行打分。打分的依据是汽车在行驶过程中所花的时间,因此代理将选择最快捷的路径到达目的地。在策略调整阶段,代理可以调整计划来避免低分,例如重新规划出发时间、出行路线、停车地点等。通过设置迭代次数来结束仿真得到分析结果。

通过MATSim中的config.xml和network.xml文件可以批量设置各个电动汽车以及地图参数,例如充电桩的位置,电动汽车的续航里程,每天的行驶总里程、出门时间、回家时间、活动范围等。通过这些设置可以很方便地模拟高达数百万车辆的行为,从而解决了传统数据统计法数据量不足以及不能反映电动汽车特性的缺陷。通过仿真最终输出以下结果:①每一段行程的出发和到达时间;②停车充电地点(地理坐标);③每一段行程的里程及持续时间,以便用来估算行程电量消耗;④行车路径。

将仿真数据通过MATSim可视化软件映射到地图上,得到用户行车模式可视化图形,可参见附录A图A1。

2 基于虚拟电池集合的充电模型

对于分布式充电模式或电动汽车接入数量较少的集中控制模式,一般采用近似线性模型对电动汽车进行建模。近似线性模型基于电池的充放电模型,将电池看成是由与荷电状态(state of charge,SOC)无关的理想电压源和内阻组成,文献[14]论证了在电动汽车接入比例不高的情况下相较于复杂的二次方程,一次线性方程已经足够用来分析其充电优化问题。但是对于大量电动汽车接入电网的情况,一般的线性化模型将带来较高的复杂度,且精度急剧下降。因此本文提出一种基于虚拟电池集合的充电需求模型。

根据第1节MATSim软件的模拟输出数据可以得出电动汽车用户行车行为存在以下规律。

1)工作日和周末。工作日上、下班出现明显的高峰时段,充电比较集中,某些充电桩负荷较高,与周末区别明显。

2)短程和长途。通过仿真和实际统计数据发现,每周工作日总行驶路程超过150 km的汽车(长途)与小于150 km的汽车(短程)行车模式存在明显的差异。

在MATSim参数设计中设置仿真汽车总量为10 000,电动汽车数量为2 500(电动汽车渗透率为25%),短程汽车数量为2 000,长途汽车数量为500,因此总共有17 500种行为模式,其中电动汽车的行为模式占到超过总数的50%。将每一种模式表示成24维距离向量,通过设置合适的k值和欧式距离,对这17 500种模式采用k-means聚类算法进行聚合归类,从而得到具有代表性的虚拟集合模型[15]。本文中采用聚类算法优化得到32个工作日集合模式和7个周末集合模式(短途),9个工作日集合模式和4个周末集合模式(长途)。

文献[16]提出了虚拟电池集合的概念及数学表达。虚拟电池集合模型基于各个集合制定能量和功率的约束条件,式(1)表示虚拟电池集合模型在节点n处的能量动态。

∀n,∀t

(1)

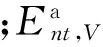
电能约束条件为:

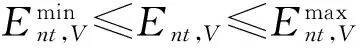
(2)

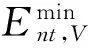
功率约束条件为:

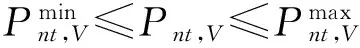
(3)

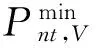
通过模拟电动汽车进入或离开虚拟电池集合,能量动态模型表明了能量怎样从一个时间步长变化到下一个时间步长,从一个节点流到另一个节点。为了使一个控制周期T(24 h)内电动汽车所获得和消耗的电能相等,规定:

En(0),V=En(T),V∀n

(4)

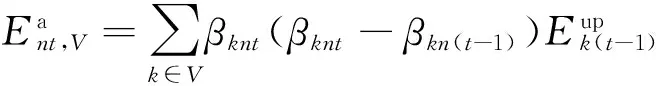
(5)

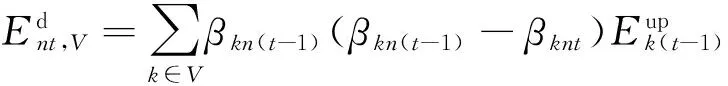
(6)

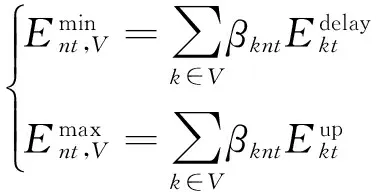
(7)

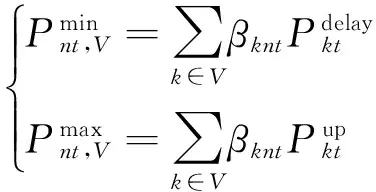
(8)

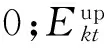
3 电动汽车充电分层控制策略

3.1 双层控制架构

现有的智能充电控制方式大体可分为集中控制和分散控制模式。附录B表B1分析了2种控制方式的优缺点。综合考虑集中式和分散式模式的优缺点,本文提出一种混合式的分层智能充电模式。即将充电控制分成多个阶段进行优化,在不同的阶段应用不同的控制策略。分层控制策略分为上、下2个层级,如图1所示。

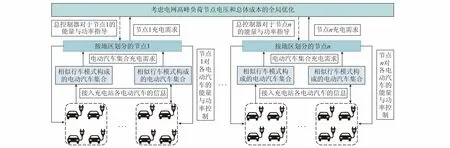
图1 电动汽车充电分层控制策略Fig.1 Hierarchical control strategy for electric vehicle charging

上层集中控制器考虑全局利益,以电网高峰负荷、节点电压和总体成本为目标进行总体优化。各节点则起承上启下的作用,负责将下层各集合的信息传输到上层集中控制器,并以从上层得到的能量与功率优化数据为约束条件,以各电动汽车充电需求得到满足为目标进行充电控制。

下层根据各电动汽车的行车习惯进行集合划分。当一辆属于集合V的电动汽车在时刻t连接到属于节点n的充电桩,通过电动汽车电池管理系统可获得电池的容量Ckn和初始SOC(Sknt0),从而可计算出初始能量Eknt0=CknSknt0。用户还要求通过充电桩交互系统输入出发时间和出发时的SOC值。

3.2 双层控制算法

根据各节点传送的各个集合充电需求信息,上层集中控制器以全局利益为目标进行能量配置优化,从而为下层分布式节点控制提供约束条件。以高峰负荷数值、节点电压波动和总体充电费用综合最低为目标的目标函数及约束条件如下所示。

(9)

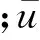
目标函数由电网总体高峰负荷、配电网总体电压波动,以及总体充电费用构成。在上层控制中,由于采用虚拟电池集合模型,使得需要考虑的变量大大减少。在式(9)中仅需考虑4个变量,因此可以采用一般的规划方法进行求解。对于下层控制来说,一个系统中节点个数从几十到几百不等,管理的电动汽车更是成千上万,因此本文采用一种扩展性和灵活性都很强的ADMM算法来对单个电动汽车充电进行控制,且使其符合上层控制所得出的功率与能量优化结果[17]。ADMM综合了对偶分解和拉格朗日增广算法的优点,采用分解—协作的模式对许多局部问题进行协调,从而找到一个全局最优解。ADMM算法具体求解步骤见附录C。

4 仿真算例

4.1 参数与场景设置

本文采用18节点系统来比较验证分层控制策略的有效性。18节点系统由18个节点、17条线路组成,如附录D图D1所示[18]。图中标出了各线路的长度以及某些节点的电压和线路高峰负荷率(标幺值)。为了简单起见,本文只选取了几个具有代表性的节点和线路进行分析,分别是节点2,3,5,7,10,11,13,16和线路1-2,3-5,2-10,10-16,11-12,16-17。根据实际情况,假设电池容量分别为32 kW·h,24 kW·h和16 kW·h三种,比例分别为40%,30%,30%。充电功率最大值为10 kW/h,最小值为1 kW/h。充电效率为90%,SOC最小值和最大值分别为0.2和1。其他参数见附录D表D1。

为了验证分层充电控制策略的有效性,考虑以下4个场景进行对比分析。

1)不控充电模式。此种模式下,电动汽车连接到充电桩即开始充电,直到充满电结束。

2)集中控制充电模式。选取本文中的上层控制策略式(9)中目标函数进行充电优化控制。

3)分散控制充电模式。选取文献[19]中提出的分散控制策略进行对比。

4)本文提出的分层充电控制策略。

4.2 仿真结果

仿真在CPU为Intel Core i3(3.6 GHz)、8 GB内存的电脑上完成,利用MATLAB中的CVX包优化求解。

附录D图D2给出了4种充电模式下18节点系统高峰时刻节点电压和线路负荷潮流状况。由此可以得到以下结果。

1)在不控模式下,所分析线路负荷全部超过额定负荷,线路1-2,2-10 甚至是额定负荷的200%。所有检测节点电压均低于额定电压的95%,节点2甚至低于额定电压的90%。这表明对于大量电动汽车接入的配电网,若不进行充电控制,电网的安全和稳定将面临严重威胁。

2)采用集中控制和分散控制时,大部分节点电压和线路负荷均处于正常范围内,但仍存在个别节点和线路不满足系统要求,如节点2和线路1-2,2-10。

3)采用分层控制策略时,高峰时所有节点与线路均处于安全状况,且与集中控制和分散控制相比具有更大的安全裕量。

选取节点2来分析日负荷曲线的变化,图2为4种充电模式下考虑常规负荷和充电负荷的日负荷曲线图。图中各曲线由总共96个点的(每15 min取1次点)多项正弦拟合而成。从图中可以看出,不控模式在10:00和19:00出现2个负荷尖峰,且超过变压器容量1 250 kW。这是因为不控模式下电动汽车充电集中在上午到达工作地点和晚上回到家之后这2个时间段。集中控制模式和分散控制模式下,最高负荷在变压器容量1 250 kW左右,集中控制模式在18:00左右达到1 300 kW。采用分层控制模式可充分利用负荷低谷期进行充电,避免了负荷高峰期,从图中可以看到,分层控制模式下在10:00达到负荷高峰1 140 kW,未超过变压器最大容量。

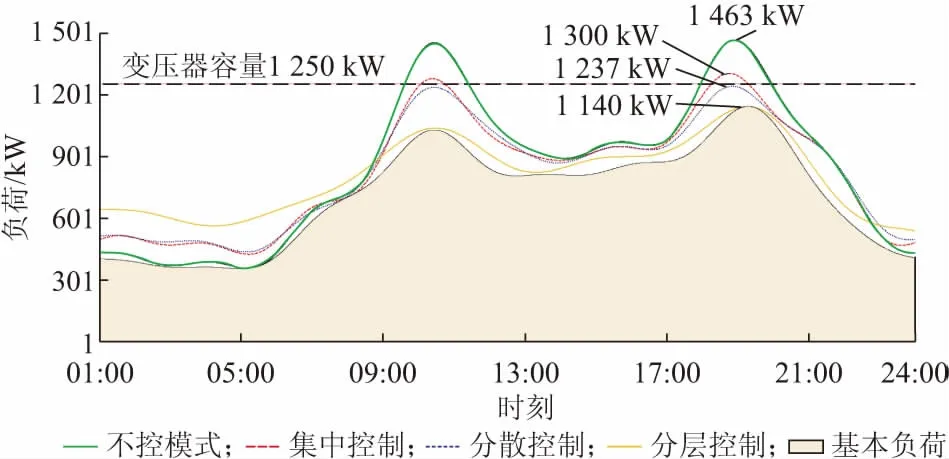
图2 不同充电模式下日负荷曲线变化Fig.2 Variation of daily load curve under different charging modes

5 结论

考虑充电行为的随机性,本文采过MATSim软件模拟电动汽车用户的行车模式,结合集中充电控制和分散充电控制策略的特点,提出了一种混合式的分层控制策略,对电动汽车充电进行优化。通过MATLAB模拟18节点配电系统,分析比较了4种充电控制模式,并得出以下结论。

1)相较于3种智能控制模式,不控模式下电网线路和节点电压均超过系统限值,严重危害电网的安全稳定运行。

2)相对于集中控制和分散控制,分层控制能更有效地减小线路负荷的增加和节点电压的降低,从而增加系统稳定裕度。

3)在3种智能充电模式中,集中控制模式会引起新的负荷高峰。分层控制相较于集中控制和分散控制可使日负荷曲线更加平滑,并能更好地实现削峰填谷。

本文所提的双层控制策略对通信要求较高,在后续的工作中将进一步研究基于本地现有通信条件的改进控制策略,同时研究分布式电源接入对于智能充电的影响。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] International Energy Agency. Key world energy statistics—2015[R/OL].[2017-03-07]. http://www.iea.org/statistics/.

[2] 中国储能网新闻中心.电动汽车销量数据分析及2016展望[EB/OL].[2017-11-02].http://www.escn.com.cn/news/show-300405.html.

[3] 马玲玲,杨军,付聪,等.电动汽车充放电对电网影响研究综述[J].电力系统保护与控制,2013,41(3):140-148.

MA Lingling, YANG Jun, FU Cong, et al. Review on impact of electric car charging and discharging on power grid[J]. Power System Protection and Control, 2013, 41(3): 140-148.

[4] 李正烁,郭庆来,孙宏斌,等.计及电动汽车充电预测的实时充电优化方法[J].电力系统自动化,2014,38(9):61-68.DOI:10.7500/AEPS20130506019.

LI Zhengshuo, GUO Qinglai, SUN Hongbin, et al. Real-time charging optimization method considering vehicle charging prediction[J]. Automation of Electric Power Systems, 2014, 38(9): 61-68. DOI: 10.7500/AEPS20130506019.

[5] KIAEE M, CRUDEN A, SHARKH S. Estimation of cost savings from participation of electric vehicles in vehicle to grid (V2G) schemes[J]. Journal of Modern Power Systems and Clean Energy, 2015, 3(2): 249-258.

[6] 孙晓明,王玮,苏粟,等.基于分时电价的电动汽车有序充电控制策略设计[J].电力系统自动化,2013,37(1):191-195.

SUN Xiaoming, WANG Wei, SU Su, et al. Coordinated charging strategy for electric vehicles based on time-of-use price[J]. Automation of Electric Power Systems, 2013, 37(1): 191-195.

[7] 刘月贤,王天钰,杨亚宇,等.电动汽车充放电系统建模与仿真[J].电力系统保护与控制,2014,42(13):70-76.

LIU Yuexian, WANG Tianyu, YANG Yayu, et al. Modeling and simulation of electric vehicles’ charge and discharge system[J]. Power System Protection and Control, 2014, 42(13): 70-76.

[8] ZUCCARO L, GIORGIO A D, LIBERATI F, et al. Smart vehicle to grid interface project: electromobility management system architecture and field test results[C]// IEEE International Electric Vehicle Conference, December 17-19, 2014, Florence, Italy.

[9] LOPES P, SOARES F J, ALMEIDA R, et al. Smart charging strategies for electric vehicles: enhancing grid performance and maximizing the use of variable renewable energy resources[C]// Hybrid and Fuel Cell Electric Vehicle Symposium, May 13-16, 2009, Stavanger, Norway.

[10] 许少伦,严正,张良,等.采用拉格朗日松弛法的电动汽车分散优化充电策略[J].电力建设,2015,36(7):107-113.

XU Shaolun, YAN Zheng, ZHANG Liang, et al. Decentralized optimization charging strategy based on Lagrangian relaxation method[J]. Electric Power Construction, 2015, 36(7): 107-113.

[11] 杨晓东,张有兵,任帅杰,等.含高渗透率光伏发电并网型微网中的电动汽车优化调度方法[J].电力系统自动化,2016,40(18):15-23.DOI:10.7500/AEPS20151102011.

YANG Xiaodong, ZHANG Youbing, REN Shuaijie, et al. Optimal scheduling scheme of electric vehicles in grid-connected microgrid with high penetration photovoltaic power[J]. Automation of Electric Power Systems, 2016, 40(18): 15-23. DOI: 10.7500/AEPS20151102011.

[12] US Department of Transportation. National household travel survey[EB/OL]. [2017-11-02]. http://nhts.ornl.gov.

[13] RIESER M, DOBLER C, DUBERNET T, et al. MATSim user guide[Z]. Switzerland: Eidgenössische Technische Hochschule Zürich, 2015.

[14] 鲍谚,姜久春,张维戈,等.电动汽车移动储能系统模型及控制策略[J].电力系统自动化,2012,36(22):36-43.

BAO Yan, JIANG Jiuchun, ZHANG Weige, et al. Model and control strategy of electric vehicle mobile energy storage system[J]. Automation of Electric Power Systems, 2012, 36(22): 36-43.

[15] KRISTOFFERSEN T K, CAPION K, MEIBOM P. Optimal charging of electric drive vehicles in a market environment[J]. Applied Energy, 2011, 88(5): 1940-1948.

[17] BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations & Trends in Machine Learning, 2011, 3(1): 1-122.

[18] SORTOMME E, HINDI M M, MACPHERSON S. Coordinated charging of plug-in hybrid electric vehicles to minimize distribution system losses[J]. IEEE Transactions on Smart Grid, 2011, 2(1): 198-205.

[19] WEN C K, CHEN J C, TENG J H, et al. Decentralized plug-in electric vehicle charging selection algorithm in power systems[J]. IEEE Transactions on Smart Grid, 2012, 3(4): 1779-1789.

何 西(1986—),男,通信作者,博士研究生,主要研究方向:智能电网、大数据在电力系统中的应用。E-mail： forevermau@163.com

涂春鸣(1976—),男,教授,博士生导师,主要研究方向:智能电网、电力电子在电力系统中的应用。E-mail: chunming_tu@263.net

王丽丽(1993—),女, 硕士研究生,主要研究方向:电动汽车、配电网优化运行与控制。E-mail: 2274458196@qq.com