基于微网的电动汽车与电网互动技术
2018-02-27周天沛
周天沛, 孙 伟
(1. 徐州工业职业技术学院机电工程学院, 江苏省徐州市 221140; 2. 中国矿业大学信息与控制工程学院, 江苏省徐州市 221008)
0 引言
由于电动汽车具有环保和节能的优点,得到了广泛的发展。不同于传统燃油汽车,电动汽车采用对车载蓄电池充电进行能量补充。由于电动汽车车主的充电行为具有很强的随机性,如果电动汽车的市场占有率不是很高,这种随机性的充电行为并不会对电网的运行造成太大的影响[1]。但是随着电动汽车的日益普及,渗透率变得越来越高,这种无序充电行为会带来很多问题。首先,电动汽车的车载电池容量较大,如果大量电动汽车在同一个时段进行集中充电,会对电网产生巨大的负荷冲击,影响电网峰谷平衡[2]。其次,为了满足这些电动汽车随时充电的负荷需求,电网需要增加更多的发电容量,这将增加电网的运行成本。再次,对于电动汽车用户而言,如果他们还是采用随用随充的简单充电方式,这样会使得车主产生较高的充电成本[3]。1997年,美国特立华大学Willet Kempton教授率先提出了电动汽车与电网互动(V2G)的概念:电动汽车不再作为简单的储能资源只能进行充电,而是被看作动态的储能资源,甚至当电网供电不足时可以被视为电源[4-5]。因此,如何对数量庞大的电动汽车的充放电行为进行有效引导,实现电动汽车与电网的合理互动,达到双赢效果,将是一个重要的研究课题。
针对该问题,不少学者对此进行了深入研究,主要围绕优化电网运行为目标或者是以经济性为目标对电动汽车充放电行为进行研究。文献[6]以最小配电网损耗为优化目标建立电动汽车有序充放电控制模型。文献[7]提出基于敏感度矩阵的电动汽车充放电控制策略,并以此建立了以减小充电对配电网节点电压的影响为优化目标的充放电优化控制模型。在以电网运行经济性为优化目标的研究中,文献[8]建立了包含充电电能成本、电网损耗成本等因素在内以充电总成本最小为优化目标的电动汽车充放电优化控制模型。文献[9]以智能住宅内的微网系统为研究对象,建立了以发用电总成本最小为目标的优化模型。
上述电动汽车的充放电优化模型多采用单目标优化模型,存在着一定的局限性。因此本文提出了三个优化目标:①微网负荷波动最小,即微网内部电能供需的平衡度最佳;②可再生能源利用率最大,这样从外部电网购电量就最少,可有效降低成本;③车主获得的收益最大。为实现这些优化目标,本文首先提出了变阈值优化算法,并在此基础上进行了改进,提出了充放电速率可调优化算法。为了验证所提算法的有效性,本文将其与未采用优化算法和文献[10]提出的寻谷优化算法进行比较。比较结果证明,该算法能够通过合理的调度来解决可再生能源利用率以及微网内部电量供应和需求不平衡问题。
1 V2G的控制模式
根据电动汽车充放电控制方式的不同,V2G的控制模式主要分为以下三种模式。
1)集中控制模式
在这种模式下,某一区域内的所有电动汽车是作为一个整体接入大电网,接受大电网的能量调度[11]。这种模式的优点是增加了可供调度的容量且易于控制,对电网“削峰填谷”的效果更明显,但建设成本比较高,比较适合于较大规模的电动汽车有序充放电过程。
2)分散式模式
在这种模式下,单辆电动汽车通过智能充放电机与大电网相连,智能充放电机根据电网的可用资源和电动汽车的剩余电量等因素来综合协调该辆电动汽车的充放电行为[12]。这种模式的优点是电动汽车充放电不受时间和空间的约束,建设成本低;但由于电动汽车接入具有随机性,其控制协调难度要比集中式模式高,比较适合于较少数量的电动汽车有序充放电过程。
3)基于微网的V2G模式
在这种模式下,电动汽车并不像前两种模式,直接与大电网相连,而是通过微网与大电网相连。电动汽车主要与微网进行能量的双向交换。微网调度中心根据各个分布式电源的出力情况、负荷需求以及包括电动汽车在内的储能装置的荷电状态(SOC)来决定电动汽车是处于充电状态和放电状态[13]。同时如果微网中各个分布式电源的发电量加上电动汽车的放电量都不能满足负荷需求,微网则需要向大电网购电,相反,微网中各个分布式电源的发电量要大于负荷的需求量加上电动汽车的充电量,微网则可以向大电网售电。这种模式结合了集中控制模式和分散模式的优点,因此在本文中,电动汽车采用这种控制模式与电网进行互动。
2 电动汽车有序充放电的多目标优化模型
2.1 优化目标
1)微网负荷波动最小
将一天分为24个时段,将风力发电、光伏发电、微网基本负荷和电动汽车组成的微网等效负荷的波动最小作为优化目标[14-15]。即
minF1=
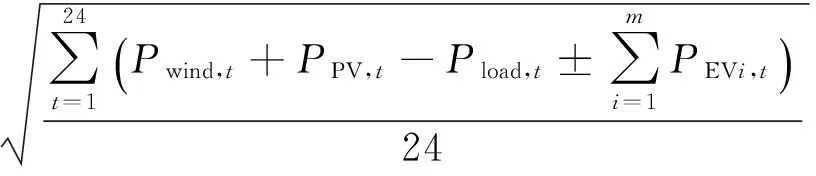
(1)
式中:m为电动汽车数量;Pwind,t为t时段风力发电机组的输出功率;PPV,t为t时段光伏阵列的输出功率;Pload,t为t时段的微网负荷消耗功率;PEVi,t为t时段内第i辆电动汽车的充/放电功率(充电时取负号,放电时取正号)。
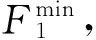
(2)
式中:α的值越小,表示微网负荷波动越小。
2)可再生能源利用率最大
为充分发挥可再生能源在电动汽车有序充放电控制中的作用和效益,本文将最大化可再生能源出力作为优化目标之一。即
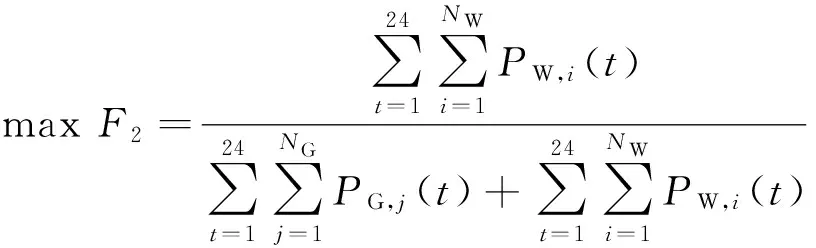
(3)
式中:NW为系统内可再生能源发电单元的数量;PW,i(t)为第i个可再生能源发电单元在t时段的出力;NG为系统内火电机组数量;PG,j(t)为第j个火电机组在t时段的出力。
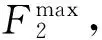
(4)
式中:β的值越小,表示可再生能源利用率越大。
3)车主获得的收益最大
电动汽车车主为了能够获得一定的经济收益,一般会选择在电价较低时进行充电,电价较高时进行放电[16]。在本文中,将一天划分为24个时段,电动汽车车主在每个时段可以根据实时电价,选择充电或是放电来实现与电网或微网的能量交换,其优化目标是使车主获得的经济收益最大。
maxF3=
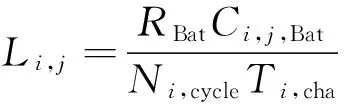
(5)
式中:Si,j为第i辆电动汽车在j时刻的售电收益;Ci,j为第i辆电动汽车在j时刻的充电成本;Li,j为第i辆电动汽车蓄电池在j时刻的损耗费用;Ri,j,dis为第i辆电动汽车在j时刻向电网的售电价格;Pi,j,dis为第i辆电动汽车在j时刻的放电量;Ri,j,cha为第i辆电动汽车在j时刻的充电价格;Pi,j,cha为第i辆电动汽车在j时刻的充电量;RBat为电动汽车蓄电池的价格;Ci,j,Bat为第i辆电动汽车蓄电池在j时刻的容量;Ti,cha为第i辆电动汽车蓄电池充满电所需时间;Ni,cycle为第i辆电动汽车蓄电池的最大充放电次数;ε为一个很小的正数。
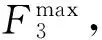
(6)
式中:γ的值越小,表示车主获得的收益越大。
当放电收益≤充电成本+蓄电池损耗费用,表示此时无收益或是收益为负,此时F3为ε,由于ε为一个很小的正数,从而保证γ的值很大,不是最优值。
综上所述,电动汽车有序充放电的多目标优化函数为:
minF=λ1α+λ2β+λ3γ
(7)
式中:λ1,λ2和λ3分别为目标函数F1,F2和F3对应的加权系数,且λ1+λ2+λ3=1。
2.2 约束条件
1)电池的可用容量约束
电动汽车车载蓄电池的容量是一定的,为了减小电池过度充电和深度放电对电池造成的不利影响,因此电池的可用容量应保持在一定的范围内[17],即
Smin≤Si,t≤Smax
(8)
式中:Si,t为第i辆电动汽车在t时刻的容量;Smin为电池容量的下限;Smax为电池容量的上限。
2)次日行驶需求约束
考虑到电动汽车车主第二天还要上班需要使用车辆,因此车辆在离开充放电站时应保持一定的最低电池容量,以满足次日行驶需求[18]。其约束条件如下:
Si,depart≥Si,set
(9)
式中:Si,depart为第i辆电动汽车离开时电池的荷电状态;Si,set为第i辆电动汽车期望荷电状态。
3)电网的功率平衡
考虑到全网的有功功率要达到平衡,其约束条件如下[19]:
Pwind,t+PPV,t+Pg,t±PEV,t-Ploss,t-Pload,t=0
(10)
式中:Pg,t为t时刻常规发电机组的输出功率;Ploss,t为网损功率;PEV,t为t时段内电动汽车的充/放电功率(充电时取负号,放电时取正号)。
3 多目标优化模型的求解
一般来说,白天时段是用电高峰期,此时电动汽车可看作发电源向微网提供电能;而在夜晚时段是用电低谷期,这时电动汽车又被看作负荷来吸收过剩的电能。在某种意义上,无论是在用电高峰时通过增加发电量提供电能,还是在用电低谷期通过增加负荷量吸收电能,都可以看作是一个“填谷”的过程。因此在进行电动汽车充放电优化控制时,会选择找寻白天时段供电曲线和夜晚时段负荷曲线的最低点,即“谷点”,然后利用电动汽车的放电或充电来实现“填谷”。该种方法可以称之为寻谷优化算法。
在该方法中,由于在某个时段内负荷/供电曲线的“谷点”是不变的,很容易出现更新的负荷曲线超过供电曲线或是更新后的供电曲线超过负荷需求的现象,这使得充放电时段被分割成多个时间段,这样算法的灵活性被大大地限制了,这使得在用电高峰期时电动汽车无法完全释放电能给微网,在用电低谷期时电动汽车无法完全吸收分布式电源发出的过剩电能,导致可再生能源的利用率降低。为了解决这个问题,本文在寻谷优化算法的基础上,提出了变阈值优化算法。
3.1 变阈值优化算法
该算法与寻谷优化算法不同的是其充放电过程是可以进行调整的。这种调整是通过改变电动汽车充/放电量的“阈值”来实现的,即如果出现寻谷优化算法中更新的负荷曲线超过供电曲线或是更新后的供电曲线超过负荷需求的现象时,可以通过增加“阈值线”的方式来保证充放电时段不被分割。为了保证安全,在电动汽车的充电过程中,该“阈值线”不能大于分布式电源的最大发电量,在放电过程中,不能大于微网中的负荷值。该算法将夜晚用电低谷期微网不含电动汽车的基本负荷的最小值作为充电过程中“阈值线”的初始值,白天用电高峰期微网分布式电源发电量的最小值作为放电过程中“阈值线”的初始值。在每一次迭代过程中,“阈值线”都会增加δ,以满足下一个时段负荷的需求和过剩风光发电能的消纳量,如式(11)和式(12)所示。
(11)
(12)
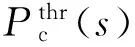
本次迭代过程的终止条件可以是参与调度的电动汽车充电至Smax或者放电至最低荷电状态Smin;也可以是当前迭代次数大于最大迭代次数。其求解过程如下:
(13)
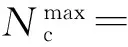
(14)
(15)
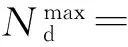
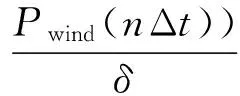
(16)
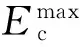
Lc(nΔt)=
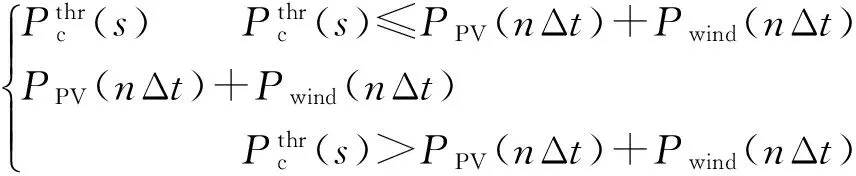
(17)
(18)
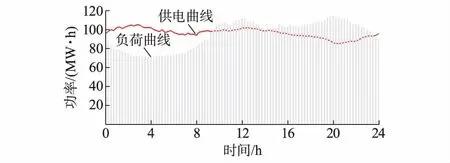
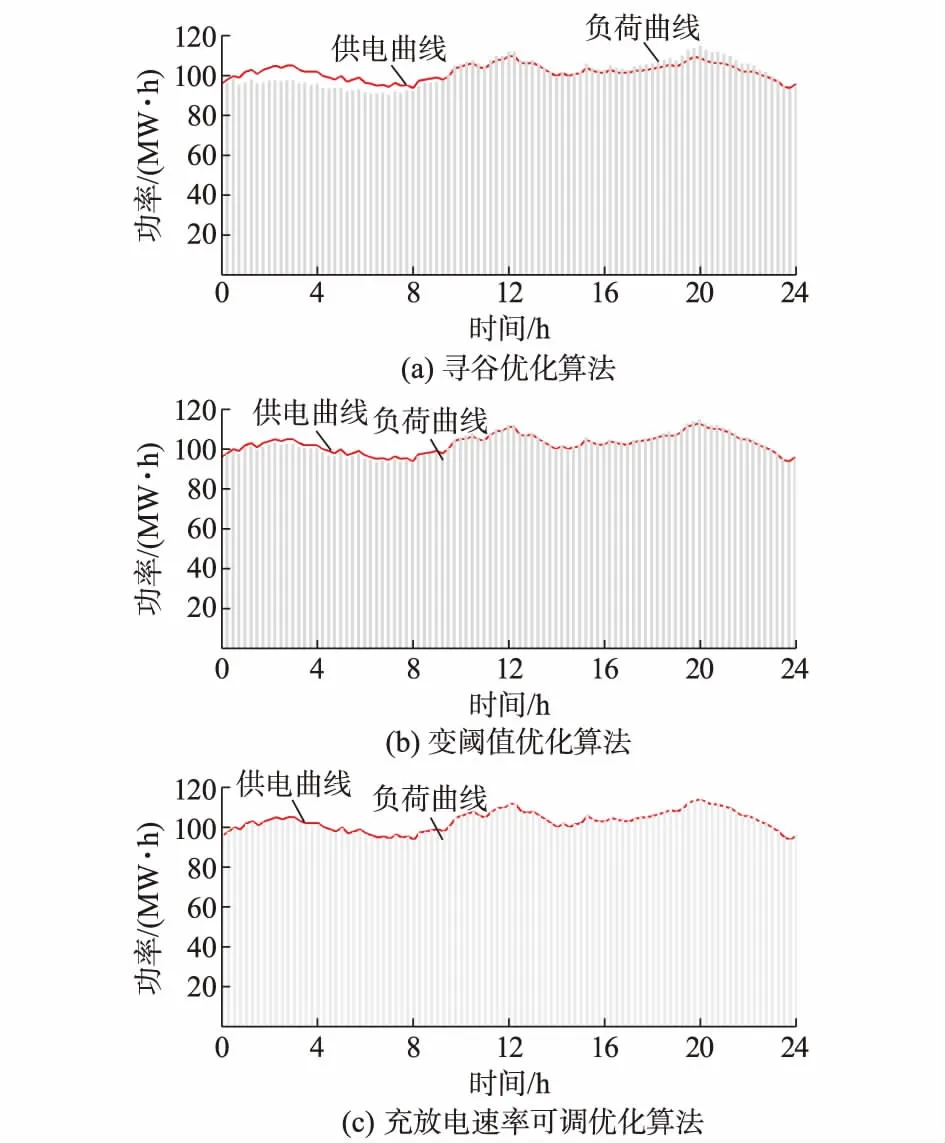
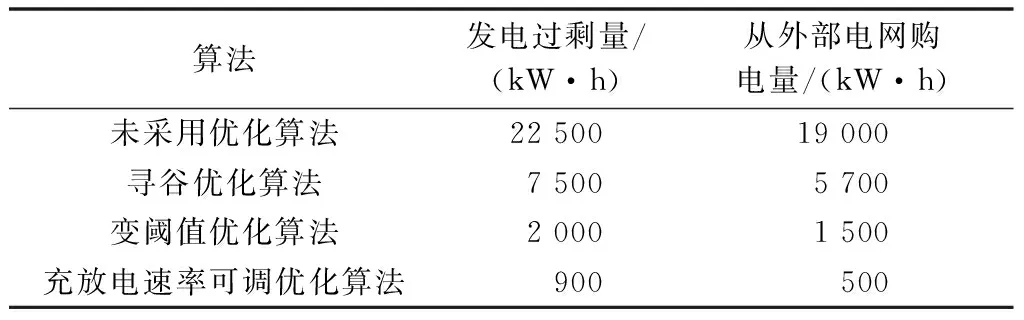
在夜晚时段(23:00至次日07:00),为吸收微网中分布式电源发出的过剩电能,电动汽车被看作负荷。在Pload(nΔt) (19) 式中:Crate为充电速率。 同理,在白天用电高峰时段(10:00—15:00,18:00—21:00),为弥补微网中分布式电源发电量的不足,电动汽车看作电源向微网供电,为了能够更加精确地供电,不造成浪费,通过将放电比较点Ld(nΔt)与当前供电量Pgen(nΔt)进行比较,找到Pgen(nΔt) (20) 式中:Drate为放电速率。 Crate,i(nΔt)=Lc(nΔt)-Pload(nΔt) (21) Drate,i(nΔt)=Ld(nΔt)-Pgen(nΔt) (22) 通过式(21)计算而得的电动汽车在充电过程中的充电速率需要满足以下两个条件:一个是该电动汽车充电速率不能超过其最大充电速率,如式(23)所示;另一个是通过该充放电速率更新的电动汽车最大充电量不能大于电池容量的上限Smax,如式(24)所示。 (23) (24) 如果不能满足以上两个条件,可以采用式(25)和式(26)进行修正。 (25) (26) 同理,电动汽车放电速率也需要满足以下两个条件:一个是该电动汽车放电速率不能超过其最大放电速率,如式(27)所示;另一个是通过该放电速率更新的电动汽车最大剩余电量不能小于最低荷电状态Smin,如式(28)所示。 (27) (28) 如果不能满足以上两个条件,可以采用式(29)和式(30)进行修正。 (29) (30) 当参与微网能量调度的电动汽车完成一次充电或放电后,当前的负荷曲线、最大充电量和供电曲线、最大剩余电量都要进行更新。更新公式如下: (31) (32) 算法流程如附录A图A1所示。 以某一区域的微网为例,该微网的分布式发电源由60台风力发电机和1 000个光伏阵列组成,单个风力发电机的额定功率为100 kW,其对应的切入风速、切出风速和额定风速分别为3.5,25,15 m/s。光伏阵列由4×5光伏电池板组成,其额定功率为4 kW。该区域内参与V2G服务的电动汽车数量为2 000辆,其电池的容量为20 kW·h,其价格为2 000元/(kW·h),最大充放电次数为1 000次。由于电动汽车不可能24 h都在充电站,需要正常出行,一般来说,大部分电动汽车主要以上下班为主要使用目的,可设定每天07:00—09:00和17:00—19:00为上下班时段,电动汽车处于行驶状态。根据有关资料,私家车的日平均行驶里程约为40 km,上下班时段各为20 km,电动汽车蓄电池每千米耗电量为0.15 kW·h,电动汽车上下班分别需要消耗电能3 kW·h,折算到荷电状态为0.15[20]。因此为了保证安全出行,电池的初始荷电状态设为0.6,电池的最低荷电状态设为0.2,电动汽车蓄电池的额定充放电速率均为0.2C(4 kW),最大充放电速率均为0.25C(5 kW)。此外该微网的日负荷功率值(Δt=15 min为间隔)如附录A表A1所示。 为验证本文所提算法的效果,本文将未采用优化算法、寻谷优化算法、变阈值优化算法和充放电速率可调优化算法来比较控制效果,未采用优化算法下的微网供电/负荷曲线变化情况如图1所示,而采用优化算法下的供电曲线/负荷曲线变化情况如图2所示。 图1 未采用优化算法下的微网供电/负荷曲线变化情况Fig.1 Power/load change curves of microgrid without optimization algorithm 图2 不同优化算法下微网供电/负荷曲线变化情况Fig.2 Power/load change curves of microgrid adopting different optimization algorithms 从图1可以看出,电动汽车如果没有参加充放电优化控制,在白天用电高峰期,微网内部各分布式电源发出的电能远不能满足负荷的需求,需要向大电网购买电量,使得微网运行成本大大增加,而到了夜晚用电低谷期,微网内部各分布式电源发出的电能又远超过负荷的需求,导致这部分能量无法使用,不得不丢弃,使得可再生能源的利用率不能得到有效的利用。其供电曲线和负荷曲线波动性较大,且存在很大的不平衡性。 当微网中的电动汽车参与充放电调度时,就可以在白天用电高峰期向微网增加电能供应量或者在夜晚用电低谷期增加从微网电能吸收量,可以实现V2G在负荷高峰期放电、负荷低谷充电的作用。从图2可以看出,如果采用寻谷优化算法,其供电曲线和负荷曲线波动性与图1相比,波动性大为降低。但是微网中的供电曲线和负荷曲线仍存在一定的不平衡度。而本文提出的变阈值优化算法和充放电速率可调优化算法可以更好地改善微网内部供电曲线和负荷曲线的平衡度,从图2(b)和图2(c)可以看出,供电曲线和负荷曲线基本吻合,尤其是变充放电速率调度算法控制效果最佳。究其原因,是因为这两种算法都可以调整充放电过程,其中充放电速率调度算法还可以调整充放电速率,这使得电动汽车有了更大的自由度根据微网的供电和负荷情况来释放或吸收电能,因此可以很好地解决可再生能源发电和电动汽车充放电的随机性问题以及微网内部电量供求不平衡问题。 本模型的第2个优化目标是可再生能源利用率最大,要想实现该目标,就需要分布式电源中的可再生能源发出的电量要尽量使用,不要有过剩电量存在,同时也要尽量少从外部电网购电。表1为不同算法下的分布式电源过剩发电量和从外部电网购电量。 表1 分布式电源过剩发电量和从外部电网购电量Table 1 Excess generation for distributed generatorand purchase of electricity from main grid 从表1中可以看出,如果该微网中没有电动汽车进行调度,其分布式电源过剩发电量和从外部电网购电量都是最高的,这说明不含电动汽车调度的微网存在较大的能量使用不平衡性。而寻谷优化算法、变阈值优化算法和充放电速率可调优化算法下的分布式电源过剩发电量相对于不含电动汽车的情况分别下降了66.7%,91.1%,96%,从外部电网购电量分别下降了70%,92.1%,97.4%。从下降幅度可以看出,充放电速率可调优化算法的性能指标是最好的。 本模型的第3个优化目标是车主获得的收益最大,要想实现该目标,需要车主在电价较低时进行充电,电价较高时向电网售电。一天中电动汽车通过微网从外部电网购电和向外部电网售电分为谷时、平时和峰时三个时段,根据国网北京市电力公司的数据,各个时段的分时购电、售电电价如附录A表A2所示,每位车主每月获得的平均收益如表2所示。 当微网中的电动汽车不参与充放电调度时,车主只能从电网购电来满足电动汽车的充电需求,其收益为负值。而当车主参与V2G服务后,其将获得一定的收益,但是由于车主参与V2G服务会造成电池额外的充放电,使得电池的损耗成本有所增加,从表2中可以看出,采用寻谷优化算法时,由于充放电过程不可以调整,其收益仍为负值,而采用了后两种优化算法,充放电过程可以根据实际情况进行调整,其中充放电速率调度算法还可以调整充放电速率,使得充放电次数减少,从而有效降低电池的损耗成本,其收益为正值,这与前面的分析基本相同。 表2 每位车主每月获得的平均收益Table 2 Average benefit of each electric vehicleowner per month 为了有效地引导电动汽车有序充放电,即电动汽车在用电高峰期作为发电源向电网供电,在用电低谷期作为负荷从电网吸收电能,实现电动汽车与电网之间的合理互动。本文重点对基于微网的V2G模式进行了研究,建立了以微网负荷波动最小、可再生能源利用率最大及车主获得的收益最大为优化目标的多目标优化模型。针对该优化模型的求解,提出了变阈值优化算法,并在此基础上进行了改进,提出了充放电速率可调优化算法用于协调电动汽车与微网之间的能量交换。优化结果表明,这两种充放电优化算法都能够在一定程度上增加可再生能源利用率,改善微网内部电量供应和需求不平衡问题以及提高电动汽车车主的收益,其中以变充放电速率调度算法的控制效果最佳。在本文中与微网进行能量交换的电动汽车主要是私家电动汽车,并未考虑公交车、出租车等不同类型的电动汽车。在未来研究过程中,要充分考虑不同类型的电动车汽车的充放电行为,并根据其充放电行为研究更为合理的调度算法。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 [1] 杨玉红,张峰,张艳芳.电动汽车参与电网调峰的分析研究[J].电力学报,2012,38(4):306-309. YANG Yuhong, ZHANG Feng, ZHANG Yanfang. Analysis of power grid peak shaving with electric vehicles[J]. Journal of Electric Power, 2012, 38(4): 306-309. [2] 刘利兵,刘天琪,张涛,等.计及电池动态损耗的电动汽车有序充放电策略优化[J].电力系统自动化,2016,40(5):83-90.DOI:10.7500/AEPS20150324001. LIU Libing, LIU Tianqi, ZHANG Tao, et al. Orderly charging and discharging strategy optimization for electric vehicles considering dynamic battery-wear model[J]. Automation of Electric Power Systems, 2016, 40(5): 83-90. DOI: 10.7500/AEPS20150324001. [3] 吴红斌,侯小凡,赵波,等.计及可入网电动汽车的微网系统经济调度[J].电力系统自动化,2014,38(9):77-84.DOI:10.7500/AEPS20130911002. WU Hongbin, HOU Xiaofan, ZHAO Bo, et al. Economical dispatch of microgrid considering plug-in electric vehicles[J]. Automation of Electric Power Systems, 2014, 38(9): 77-84. DOI: 10.7500/AEPS20130911002. [4] 罗卓伟,胡泽春,宋永华,等.大规模电动汽车充放电优化控制及容量效益分析[J].电力系统自动化,2012,36(10):19-26. LUO Zhuowei, HU Zechun, SONG Yonghua, et al. Coordinated charging and discharging of large-scale plug-in electric vehicles with cost and capacity benefit analysis [J]. Automation of Electric Power Systems, 2012, 36(10): 19-26. [5] CHUKWU U C, MAHAJAN S M. Real-time management of power systems with V2G facility for smart-grid applications[J]. IEEE Transactions on Sustainable Energy, 2014, 5(2): 558-556. [6] 占恺峤,宋永华,胡泽春.以降损为目标的电动汽车有序充电优化[J].中国电机工程学报,2012,32(31):11-18. ZHAN Kaiqiao, SONG Yonghua, HU Zechun. Coordination of electric vehicle charging to minimize active power losses[J]. Proceedings of the CSEE, 2012, 32(31): 11-18. [7] KARFOPOULOS E L, PANOURGIAS K A, HATZIARGYRIOU N D. Distributed coordination of electric vehicles providing V2G regulation services[J]. IEEE Transactions on Power Systems, 2016, 31(4): 2834-2846. [8] CROW M M L. Cost-constrained dynamic optimal electric vehicle charging[J]. IEEE Transactions on Sustainable Energy, 2017, 8(2): 716-724. [9] 王姝凝,杨少兵.居民小区电动汽车充电负荷有序控制策略[J].电力系统自动化,2016,40(4):71-77.DOI:10.7500/AEPS20150429013. WANG Shuning, YANG Shaobing. A coordinated charging control strategy for electric vehicles charging load in residential area[J]. Automation of Electric Power Systems, 2016, 40(4): 71-77. DOI: 10.7500/AEPS20150429013. [10] JIN Chenrui, TANG Jian, GHOSH P. Optimizing electric vehicle charging: a customer’s perspective[J]. IEEE Transactions on Vehicular Technology, 2013, 62(7): 2919-2927. [11] ORTEGA-VAZQUEZ M A. Optimal scheduling of electric vehicle charging and vehicle-to-grid services at household level including battery degradation and price uncertainty[J]. IET Generation, Transmission & Distribution, 2014, 8(6): 1007-1016. [12] 郑颖,孙近文,张冲.考虑电动汽车接入的配电系统静态电压稳定裕度研究[J].电工技术学报,2014,29(8):20-26. ZHENG Ying, SUN Jinwen, ZHANG Chong. Study of voltage stability margin for the distribution network with electric vehicle integration[J]. Transactions of China Electrotechnical Society, 2014, 29(8): 20-26. [13] 杨晓东,张有兵,任帅杰,等.含高渗透率光伏发电并网型微网中的电动汽车优化调度方法[J].电力系统自动化,2016,40(18):15-23.DOI:10.7500/AEPS20151102011. YANG Xiaodong, ZHANG Youbing, REN Shuaijie, et al. Optimal scheduling scheme of electric vehicles in grid-connected microgrid with high penetration photovoltaic power[J]. Automation of Electric Power Systems, 2016, 40(18): 15-23. DOI: 10.7500/AEPS20151102011. [14] GUO Qinglai, XIN Shujun, SUN Hongbin. Rapid-charging navigation of electric vehicles based on real-time power systems and traffic data[J]. IEEE Transactions on Smart Grid, 2014, 5(4): 1969-1979. [15] TANG Yuchen, ZHONG Jin, BOLLEN M. Aggregated optimal charging and vehicle-to-grid control for electric vehicles under large electric vehicle population[J]. IET Generation, Transmission & Distribution, 2016, 10(8): 2012-2018. [16] RIGAS E S, RAMCHURN S D, BASSILIADES N. Managing electric vehicles in the smart grid using artificial intelligence: a survey[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(4): 1619-1635. [17] BAI Xiaoqing, QIAO Wei. Robust optimization for bidirectional dispatch coordination of large-scale V2G[J]. IEEE Transactions on Smart Grid, 2015, 6(4): 1944-1954. [18] 陈静鹏,艾芊,肖斐.基于用户出行需求的电动汽车充电站规划[J].电力自动化设备,2016,36(6):34-39. CHEN Jingpeng, AI Qian, XIAO Fei. EV charging station planning based on travel demand[J]. Electric Power Automation Equipment, 2016, 36(6): 34-39. [19] 李正烁,郭庆来,孙宏斌,等.计及电动汽车充电预测的实时充电优化方法[J].电力系统自动化,2014,38(9):61-68.DOI:10.7500/AEPS20130506019. LI Zhengshuo, GUO Qinglai, SUN Hongbin, et al. Real-time charging optimization method considering vehicle charging prediction[J]. Automation of Electric Power Systems, 2014, 38(9): 61-68. DOI: 10.7500/AEPS20130506019. [20] 杨晓东,任帅杰,张有兵,等.电动汽车可调度能力模型与日内优先调度策略[J].电力系统自动化,2017,41(2):84-93.DOI:10.7500/AEPS20160323006. YANG Xiaodong, REN Shuaijie, ZHANG Youbing, et al. Schedulable ability model and priority-based intraday scheduling strategy for electric vehicle[J]. Automation of Electric Power Systems, 2017, 41(2): 84-93. DOI: 10.7500/AEPS20160323006. 周天沛(1977—),男,博士,副教授,主要研究方向:微电网优化运行、电动汽车充电站布局最优规划。E-mail: zhoutianpei_001@163.com 孙 伟(1963—),男,通信作者,博士,教授,博士生导师,主要研究方向:分布式智能微电网建设以及优化运行。E-mail: sw3883204@163.com (编辑孔丽蓓) ( continuedonpage117)( continuedfrompage104)3.2 充放电速率可调优化算法
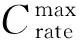
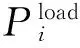
4 仿真算例

5 结论
