多光伏发电单元并联接入弱交流系统的稳定性分析

贾 祺, 严干贵, 李泳霖, 蔡玉汝, 张华鲁

(东北电力大学电气工程学院, 吉林省吉林市 132012)

0 引言

光伏发电是推进能源转型和应对环境挑战的重要途径。截至2016年底,中国光伏发电累计装机容量达到77.42 GW,预计2020年光伏装机容量达150 GW,每年新增容量20 GW左右,光伏发电呈现快速发展态势[1]。

由于受资源禀赋约束,大规模光伏发电多处于电网结构薄弱的沙漠/半沙漠地带,经逆变器并网,呈现多光伏发电单元并联结构。理想电网条件下,并网点电压较稳定,各光伏逆变器之间弱耦合,交互影响较小。随着光伏并网发电容量的增加,电网阻抗不可忽略,导致所接入电网呈现弱交流电网特性[2-3],理想电网条件被破坏。并网点电压受各光伏阵列输出功率扰动、电网扰动等多方面影响,易产生波动[4],各光伏逆变器之间强耦合,交互影响较大,多光伏发电并联运行稳定性面临挑战[5-11]。

为分析弱交流系统条件下光伏发电运行稳定性,文献[6]将光伏发电系统等效为受控电流源,提出阻抗比判据,据此分析其运行稳定性。该分析方法在小功率并网光伏系统中得到了广泛的应用[7]。文献[8]基于Nyquist稳定判据分析电网阻抗对给定控制策略下光伏发电系统运行稳定性的影响,提出一种控制器参数整定方法。文献[9]建立了光伏发电系统的诺顿等效模型,推导了逆变器并网电流和并网点电压表达式,基于光伏发电系统闭环特征方程的根轨迹分析电网阻抗对其稳定性的影响。文献[10-11]从谐振特性、动态响应和运行稳定性方面分析了电网阻抗对光伏发电系统运行特性的影响,为光伏发电规划设计提供参考。

上述研究均定性地判断了弱交流系统下光伏发电系统的运行稳定性,但并未考虑逆变器控制系统中各控制环节的交互影响。文献[12-14]指出弱交流系统下,逆变器的锁相环(PLL)和无功功率控制环会对直流电压控制起滞后作用,引起负阻尼从而减弱直流电压的稳定性。

此外,大多数研究均侧重于单机接入弱交流系统,对于多个并联接入弱交流系统鲜有研究,文献[15]基于节点导纳矩阵建立了多逆变器并联系统的频域模型,分析了集电系统中馈线的拓扑结构对逆变器电流环稳定性的影响,但未考虑各逆变器不同锁相环控制器参数对其运行稳定性的影响。

本文以两个光伏发电单元并联接入弱交流系统作为研究对象,建立其小信号模型,分析电网强度、各光伏发电单元运行工况以及各逆变器锁相环控制器参数对其稳定性的影响,揭示各光伏发电单元运行工况的耦合机制,提出一种基于虚拟端电压的光伏发电运行控制,提高多光伏发电单元运行稳定性。最后,在EMTDC/PSCAD中搭建两个光伏发电单元并联接入弱交流系统仿真模型,仿真结果对理论分析与控制策略进行了有效验证。

1 连接弱交流系统的多光伏发电单元结构

大型光伏电站通常采用的电气结构如附录A图A1所示。电站内一般包括数十乃至数百个光伏发电单元,其中每两个光伏发电单元共用一台0.38 kV/35 kV升压变压器,再经过电缆汇集至一台35 kV/110 kV主变压器升压后经输电线路(等效为一条线路)接入主网(等效为理想电源)。

附录A图A1中交流系统强度一般用短路比(SCR)描述,即交流系统短路容量Sac与光伏电站额定功率SN之比[16],如式(1)所示。

(1)

式中:Z为电网等值阻抗;UN为电网电压额定值。弱交流系统通常指SCR介于2～3之间,当SCR小于2时为极弱交流系统。

本文以其中两个光伏发电单元并联接入弱交流系统为例展开研究,如附录A图A2所示,并将输电侧的电网电压等级、线路阻抗参数以及变压器阻抗参数折算到逆变器输出侧电压等级。

2 多光伏发电单元小信号建模

多光伏发电单元小信号建模包括光伏阵列建模、逆变器及其控制系统建模、网络建模,其建模假设:①不考虑交流侧滤波电容影响;②只计及电网电抗的影响;③逆变器传输功率无损耗。

2.1 光伏阵列建模

一个并联串数为Ns,每串由Np个光伏电池组成的光伏阵列如附录A图A3所示。基于各光伏电池运行特性的一致性,得到第i个光伏阵列端口的Udci-iPVi特性方程[17]为:

(2)

式中:iPVi为光伏阵列的输出电流;Udci为光伏阵列的输出电压;Isci为短路电流;Uoci为开路电压;C1和C2为常数。

2.2 逆变器及其控制系统建模

多光伏发电单元中第i个逆变器的拓扑结构见附录A图A4,并在dq坐标系下列写逆变器数学模型如式(3)所示。

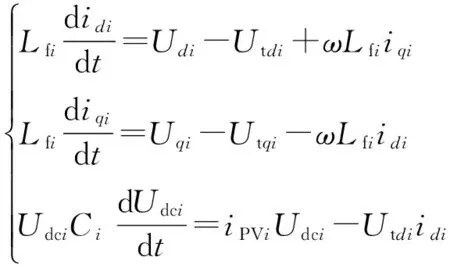
(3)

逆变器一般采用基于电网电压的定向矢量控制策略,见附录A图A5。功率外环控制根据有功功率和无功功率的需求分别生成d轴和q轴电流指令值,通过调节d轴和q轴电流来调节注入电网的有功功率和无功功率。有功功率控制采用定直流电压控制方式,无功功率控制采用恒端电压幅值控制方式。

由附录A图A5中第i个逆变器的控制策略可得其控制方程如下:

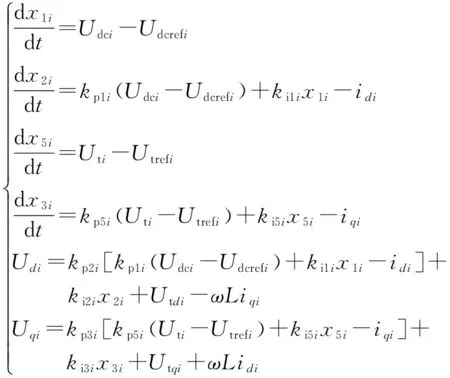
(4)

式中:x1i,x2i,x3i,x5i为状态变量;kp1i和ki1i分别为电压外环控制器的比例和积分系数；kp2i,kp3i和ki2i，ki3i分别为电流内环控制器的比例和积分系数；kp5i和ki5i分别为无功外环控制器的比例和积分系数。

2.3 锁相环建模

附录A图A5中锁相环控制模块的基本工作原理见附录A图A6,其中dq轴为两相旋转坐标轴,xy轴为两相静止坐标轴,锁相环用来跟踪交流母线电压相位,保持端电压相量与d轴重合。

锁相环控制策略如附录A图A7所示,其控制方程如式(5)所示。

(5)

式中:xpll为状态变量;ω0为系统初始角频率;kp4i和ki4i分别为锁相环控制器的比例和积分系数;θplli为锁相环产生的角度。

2.4 网络建模

附录A图A2中交流侧等值电路见附录A图A8,根据电路原理可得:

(6)

式中:xg为电网等值电抗;xci为汇集线路电抗;Utxi和Utyi分别为逆变器端电压的x轴和y轴分量;Ugx和Ugy分别为电网电压的x轴和y轴分量。

此外,逆变器端电压以及并网电流的xy轴分量Utxi,Utyi,ixi,iyi与dq轴分量Utdi,Utqi,idi,iqi满足如下关系:

(7)

综上,式(2)—式(7)构成了两个光伏发电单元并联系统的代数—微分方程组,将上述方程组在平衡点处进行线性化,得到其小信号模型,并建立如式(8)所示的状态空间方程(详见附录B)。

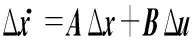
(8)

式中:Δx为状态变量;Δu为输入变量;A和B分别为状态矩阵和输入矩阵,系统的小干扰稳定性与A阵的特征根有关。

3 多光伏发电单元小干扰稳定性分析

3.1 特征根分析

系统主要参数见附录C表C1(各参数均已折算到逆变器输出侧电压等级),当SCR为1.5时,基于式(8)的状态矩阵,求得系统的特征根见附录C表C2。由该表可知,系统的所有特征根包含10个衰减模态和4个振荡模态,均分布在复平面左侧,两个光伏发电单元并联接入弱交流系统是小干扰稳定问题。

3.2 电网强度对其稳定性的影响

为分析电网强度、各光伏发电单元运行工况以及各锁相环控制器比例系数对两个光伏发电单元并联接入弱交流系统小干扰稳定性的影响,以下主要分析A阵特征根的变化规律。

当电网强度变化时系统的特征根轨迹见附录A图A9,电网强度的变化导致8个特征根发生变化。随着电网强度的降低,λ1,λ7,λ8,λ14向稳定区域移动;λ9,λ10,λ11,λ12向不稳定区域移动。当SCR为1.2时,λ9和λ10越过虚轴,进入不稳定区域,系统失去稳定。

3.3 各光伏发电单元运行工况对其稳定性的影响

当各光伏阵列运行工况变化时,系统的特征根轨迹见附录A图A10,其输出功率的变化将导致7个特征根发生变化。随着两个光伏发电单元输出功率(Pe1和Pe2)的增加,λ7,λ8,λ14向稳定区域移动;λ9,λ10,λ11,λ12向不稳定区域移动,且λ9和λ10的实部绝对值变化十分显著。

两个光伏发电单元在不同运行工况下,系统主导特征根λ9和λ10的振荡频率与阻尼比如图1所示。从图1中可知:随着两个光伏发电单元输出功率的增加,系统的阻尼比越小,系统稳定性越差。

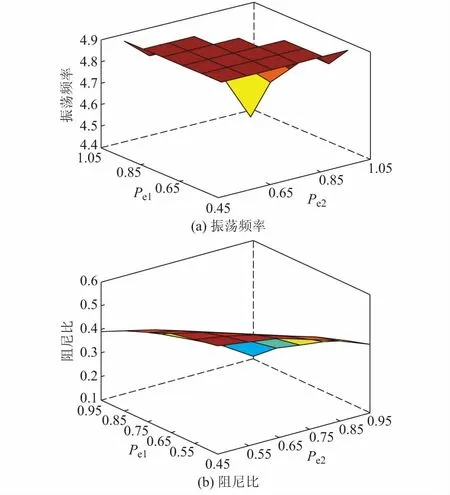
图1 运行工况变化时系统的振荡频率与阻尼比Fig.1 Oscillation frequency and damping ratio of system in varying operation state

3.4 锁相环控制器参数对其稳定性的影响

当SCR为1.5,光伏发电单元1控制系统的锁相环参数kp41变化、光伏发电单元2控制系统的锁相环参数kp42=50保持不变时,系统的特征根轨迹见附录A图A11,锁相环参数kp41的变化导致7个特征值发生变化。随着锁相环参数kp41的增加(从10增大至100),λ7,λ8,λ9,λ10,λ11,λ12向稳定区域移动,其中λ9和λ10越过虚轴;λ14向不稳定区域移动,变化不显著。当kp41=10和kp42=50时,λ9和λ10处于不稳定区域,系统不稳定。

当两个光伏发电单元锁相环参数kp41和kp42均发生变化时,系统主导特征根λ9和λ10的振荡频率、阻尼比如图2所示。从图2中可知:随着两个光伏发电单元锁相环参数kp41和kp42的增加,系统的阻尼比越大,系统越稳定。

4 多光伏发电单元并联运行耦合机制

4.1 各光伏发电单元运行工况对耦合机制的影响

为揭示两个光伏发电单元间的运行耦合机制,由各光伏发电单元输出功率(Pe1和Pe2)可知:

(9)

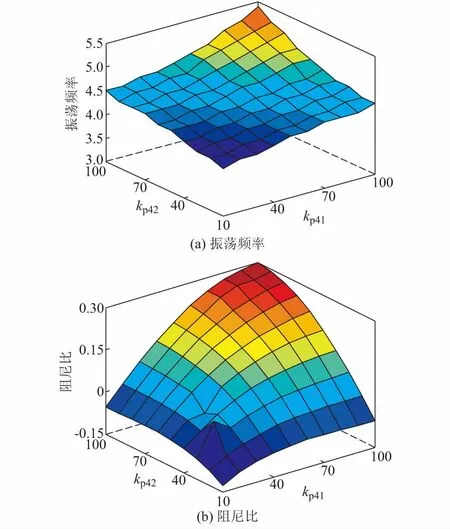
图2 锁相环参数变化时系统的振荡频率与阻尼比Fig.2 Oscillation frequency and damping ratio of system when phase-locked loop gains varying

将式(9)在平衡点处线性化,并将式(7)线性化的结果代入式(9)可得:

(10)

式中:k11至k26为与系统结构参数、运行工况有关的常数,其表达式见附录D。k11,k14,k21,k24表示电流d轴分量的变化对输出有功功率的影响;k12,k15,k22,k25表示电流q轴分量的变化对输出有功功率的影响;k13,k16,k23,k26表示锁相环输出的变化对输出有功功率的影响。

由式(10)可知,两个光伏发电单元输出功率的扰动ΔPe1和ΔPe2不仅受自身控制系统输出扰动的影响,还存在交互影响,首先考虑电流d轴分量的变化对输出有功功率的影响,简化式(10)可得:

(11)

定义k11和k24为各光伏发电单元的自耦系数,k14和k21为各光伏发电单元间的互耦系数,基于附录C表C1的系统参数,改变电网强度与光伏发电单元2的运行工况,得到如图3所示的k24和|k21|的变化曲线。由图3可知,随着电网强度的降低、光伏发电单元2运行工况的增加,自耦系数逐渐降低,互耦系数绝对值逐渐增加,两个光伏发电单元耦合紧密。

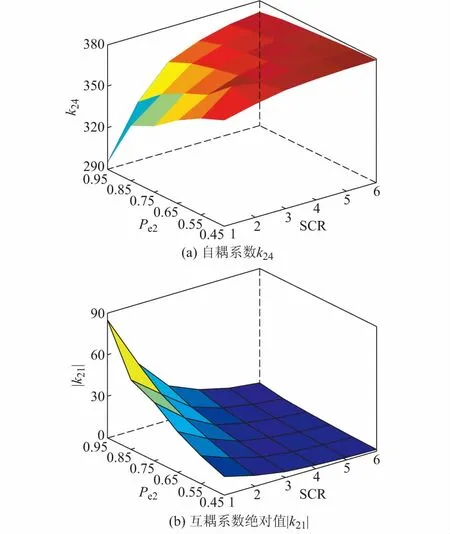
图3 k24与|k21|随光伏阵列运行工况以及电网强度的变化曲线Fig.3 Changing curves of k24 and |k21| with varying PV operation state and power grid strength

进一步分析两个光伏发电单元间互耦系数绝对值的增加对其运行稳定性的影响,定义系数k为逆变器2与逆变器1的输出扰动功率比(0≤k≤1),即

(12)

由式(12)得到Δid1与Δid2的关系如下：

(13)

将式(13)代入式(11)中可得:

(14)

考虑到根轨迹分析中不稳定现象处于低频段,并认为电流理想跟踪其参考值[18],将光伏发电单元1的功率控制环路简化,如图4所示，其中:ΔPPV1为光伏发电单元1的注入功率扰动。

当光伏发电单元1的输出功率不变,光伏发电单元2的输出功率逐渐增加,在附录C表C1给定的参数下,求得的光伏发电单元1输出功率环路的负反馈系数见附录A图A12,开环传递函数Go(s)的波特图见附录A图A13。由附录A图A12和图A13可知:随着光伏阵列2输出功率的增加,光伏发电单元间耦合紧密,导致光伏发电单元1负反馈系数逐渐减小,进而劣化其输出功率环路的相位裕度,降低其运行稳定性。

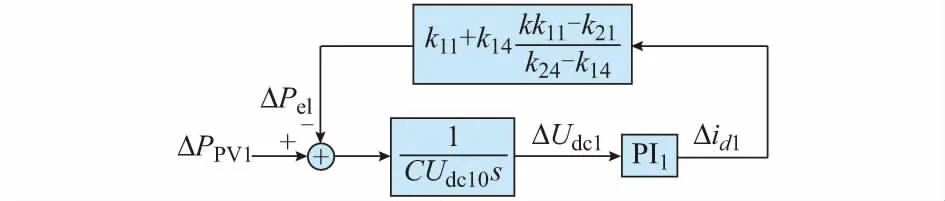
图4 光伏发电单元1的功率控制环路Fig.4 Power control loop of PV generation unit 1

4.2 各锁相环控制参数对耦合机制的影响

为分析各光伏发电单元锁相环控制对耦合系数的影响,将式(10)简化可得:

(15)

进一步整理可得:

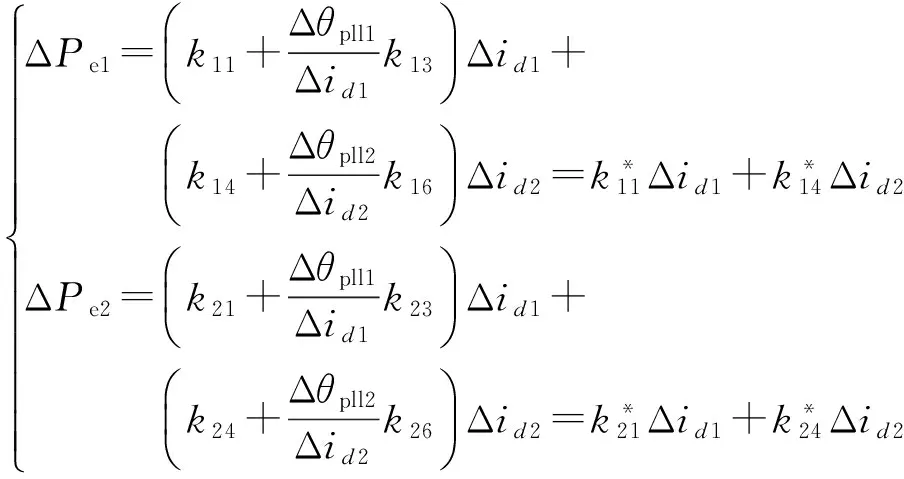
(16)

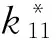
在附录C表C1给定的参数下,当两个光伏发电单元均额定运行时,不同锁相环控制器参数下,光伏发电单元2自耦系数与互耦系数的波特图如图5所示。由此可知,当锁相环控制器参数kp41=10,ki41=1 500,kp42=10,ki42=1 500时,在频率4～5 Hz范围内,光伏发电单元2的自耦系数与互耦系数变化较大,两个光伏发电单元间的耦合紧密,互耦系数对光伏发电单元1的功率环路起到正反馈作用,恶化其运行稳定性。

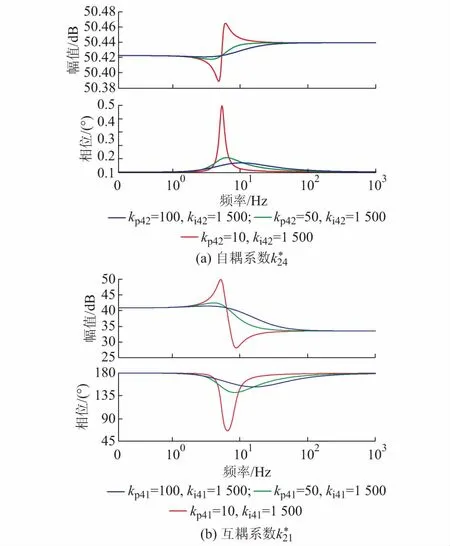
图与的波特图Fig.5 Bode diagrams of and

5 基于虚拟端电压的光伏发电运行控制

由根轨迹分析可知,通过优化逆变器控制器参数可以提高多光伏发电单元并联接入弱交流系统的运行稳定性,但弱交流系统条件下逆变器的各控制环路间交互影响,现有的优化设计方法可能并不适用。为此,本文提出一种基于虚拟端电压的光伏发电运行控制,增强系统的运行稳定性。

以单个光伏发电单元接入弱交流系统为例介绍虚拟端电压控制,其交流侧等值电路见附录A图A14(忽略集电线路的影响)。从该图可知,如果将端电压Uti前移至Utivir可等效减小电网阻抗,从而提高系统运行的稳定性,但实际系统中将端电压前移的方法难以实现。因此,在控制系统中引入虚拟端电压Utivir,等效地将主电路中的Uti前移,修改后的逆变器控制策略见附录A图A15。Uti与Utivir满足如下关系:

(17)

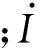
6 仿真算例验证

为验证理论分析的正确性,在EMTDC/PSCAD中搭建如附录A图A1所示的两个光伏发电单元并联接入弱交流系统的仿真模型。

6.1 电网强度不同时的仿真分析

当两个光伏发电单元锁相环控制器参数分别为kp41=50,ki41=1 500,kp42=50,ki42=1 500时,不同电网强度下两个光伏发电单元的端电压Ut1和Ut2、直流侧电压Udc1和Udc2见附录E图E1和图E2。图E1中SCR为1.5,t=8 s时两个光伏发电输出功率增加,经过衰减振荡后,系统稳定运行。图E2中SCR为1.2,t=8 s时两个光伏发电输出功率增加,系统出现振荡现象,振荡频率约为5 Hz,与理论分析基本一致。

6.2 各锁相环控制器比例系数不同时的仿真分析

当SCR为1.5时,不同锁相环控制器参数下两个光伏发电单元端电压Ut1和Ut2、直流侧电压Udc1和Udc2见附录E图E3至图E6。图E3中kp41=20,ki41=1 500,kp42=50,ki42=1 500;图E4中kp41=30,ki41=1 500,kp42=50,ki42=1 500;图E5中kp41=30,ki41=1 500,kp42=30,ki42=1 500;图E6中kp41=40,ki41=1 500,kp42=40,ki42=1 500。t=8 s时两个光伏发电单元输出功率增加,图E4和图E6经过衰减振荡后,系统稳定运行,而图E3和图E5中出现振荡现象,与理论分析基本一致。

6.3 虚拟端电压控制

当SCR为1.2,kp41=50,ki41=1 500,kp42=50,ki42=1 500,调节系数a=0.5时,两个光伏发电单元端电压Ut1和Ut2、直流侧电压Udc1和Udc22见附录E图E7。t=8 s时两个光伏发电输出功率增加,经过衰减振荡后,系统稳定运行。

当SCR为1.5,kp41=20,ki41=1 500,kp42=50,ki42=1 500,调节系数a=0.5时,两个光伏发电单元端电压Ut1和Ut2、直流侧电压Udc1和Udc22见附录E图E8。t=8 s时两个光伏发电输出功率增加,经过衰减振荡后,系统稳定运行。由此可见,虚拟端电压的引入可提高多光伏发电单元并联接入弱交流系统的运行稳定性。

7 结论

本文建立了两个光伏发电单元并联接入弱交流系统的小信号模型,分析了电网强度、锁相环控制器参数以及各光伏发电单元运行工况对其接入弱交流系统运行稳定性的影响,得到如下结论。

1)各光伏阵列输出功率的增加和电网强度的降低,易使多光伏发电单元发生振荡现象。

2)一定范围内增加各逆变器锁相环控制器比例系数(暂不考虑积分系数的影响),可增强系统阻尼,易于提高系统的稳定性。

3)多光伏发电单元间功率环路存在耦合项,易受光伏发电单元运行工况与锁相环控制器比例系数的影响,光伏发电单元运行工况增加，锁相环控制器比例系数减小,光伏发电单元间互耦系数增加,对于功率环路起到正反馈作用,劣化系统稳定性。

4)光伏发电控制系统中虚拟端电压的引入,可等效减小电网阻抗,提高系统运行稳定性。

此外,本文仍存在以下不足:①采用理想电源连接可变电感来模拟弱交流系统场景,无法充分考虑光伏发电渗透率对其运行稳定性的影响;②对于锁相环控制器影响光伏发电单元间的互耦系数,本文给出定性判断,缺乏量化分析,有待进一步完善。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 国家能源局.2015年光伏发电相关统计数据[EB/OL].[2017-03-26].http://www.nea.gov.cn/2016-06/27/c_135469557.htm.

[2] 周林,张密,杨明,等.考虑电网阻抗影响的LCL型并网逆变器控制策略[J].太阳能学报,2015,36(9):2146-2151.

ZHOU Lin, ZHANG Mi, YANG Ming, et al. Controller design of three-phase inverter with LCL filter considering the grid impedance[J]. Acta Energiae Solaris Sinica, 2015, 36(9): 2146-2151.

[3] 赵争鸣,雷一,贺凡波,等.大容量并网光伏电站技术综述[J].电力系统自动化,2011,35(12):101-107.

ZHAO Zhengming, LEI Yi, HE Fanbo, et al. Overview of large-scale grid-connected photovoltaic power plants[J]. Automation of Electric Power Systems, 2011, 35(12): 101-107.

[4] 黄云辉,周翩,王龙飞.弱电网下基于矢量控制的并网变换器功率控制稳定性[J].电力系统自动化,2016,40(14):93-99.DOI:10.7500/AEPS20150719001.

HUANG Yunhui, ZHOU Pian, WANG Longfei. Power control stability in vector control based voltage source converters connected to weak grid[J]. Automation of Electric Power Systems, 2016, 40(14): 93-99. DOI: 10.7500/AEPS20150719001.

[5] 杨明,周林,张东霞,等.考虑电网阻抗影响的大型光伏电站并网稳定性分析[J].电工技术学报,2013,28(9):214-223.

YANG Ming, ZHOU Lin, ZHANG Dongxia, et al. Stability analysis of large-scale photovoltaic power plants for the effect of grid impedance[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 214-223.

[6] SUN Jian. Impedance-based stability criterion for grid-connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078.

[7] HE Jinwei, LI Yunwei, BOSNJAK D, et al. Investigation and active damping of multiple resonances in a parallel-inverter-based microgrid[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 234-246.

[8] 严干贵,李龙,黄亚峰,等.弱电网下联网光伏逆变系统稳定性分析及控制参数整定[J].太阳能学报,2013,34(11):1853-1859.

YAN Gangui, LI Long, HUANG Yafeng, et al. Stability analysis and control parameters tuning of grid-connected photovoltaic inverter system in weak grid[J]. Acta Energiae Solaris Sinica, 2013, 34(11): 1853-1859.

[9] 周林,张密,居秀丽,等.电网阻抗对大型并网光伏系统稳定性影响分析[J].中国电机工程学报,2013,34(34):34-41.

ZHOU Lin, ZHANG Mi, JU Xiuli, et al. Stability analysis of large-scale photovoltaic plants due to grid impedances[J]. Proceedings of the CSEE, 2013, 34(34): 34-41.

[10] 严干贵,常青云,黄亚峰,等.弱电网接入下多光伏逆变器并联运行特性分析[J].电网技术,2014,38(4):933-940.

YAN Gangui, CHANG Qingyun, HUANG Yafeng, et al. Analysis on parallel operational characteristics of multi photovoltaic inverters connected to weak-structured power system[J]. Power System Technology, 2014, 38(4): 933-940.

[11] AGORRETA J L, BORREGA M, LOPEZ J, et al. Modeling and control ofN-paralleled grid-connected inverters with LCL filter coupled due to grid impedance in PV plants[J]. IEEE Transactions on Power Electronics, 2011, 26(3): 770-785.

[12] HUANG Yunhui, YUAN Xiaoming, HU Jiabing, et al. DC-bus voltage control stability affected by AC-bus voltage control in VSCs connected to weak AC grids[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(2): 445-458.

[13] HU Jiabing, HUANG Yunhui, WANG Dong, et al. Modeling of grid-connected DFIG-based wind turbines for DC-Link voltage stability analysis[J]. IEEE Transactions on Sustainable Energy, 2015, 6(4): 1325-1336.

[14] ZHOU J Z, DING Hui, FAN Shengtao, et al. Impact of short-circuit ratio and phase-locked-loop parameters on the small-signal behavior of a VSC-HVDC converter[J]. IEEE Transactions on Power Delivery, 2014, 29(5): 2287-2296.

[15] 严亚兵,苗淼,袁小明.新能源电站集电馈线对多变流器并网运行稳定性的影响[J].电力系统自动化,2016,40(15):86-92.DOI:10.7500/AEPS20150815006.

YAN Yabing, MIAO Miao, YUAN Xiaoming. Impact of renewable power plant collector system on stability of grid-connected multi-converters[J]. Automation of Electric Power Systems, 2016, 40(15): 86-92. DOI: 10.7500/AEPS20150815006.

[16] IEEE guide for planning DC links terminating at AC locations having low short-circuit capacities: IEEE Standard 1204—1997[S]. 1997.

[17] 谢宁,罗安,陈燕东,等.大型光伏电站动态建模及谐波特性分析[J].中国电机工程学报,2013,33(36):10-17.

XIE Ning, LUO An, CHEN Yandong, et al. Dynamic modeling and characteristic analysis on harmonics of photovoltaic power stations[J]. Proceedings of the CSEE, 2013, 33(36): 10-17.

[18] HUANG Yunhui, YUAN Xiaoming, HU Jiabing, et al. Modeling of VSC connected to weak grid for stability analysis of DC-link voltage control[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(4): 1193-1204.

贾 祺(1991—),男,博士研究生,主要研究方向:新能源发电联网运行分析与控制技术。E-mail： 15948692960@163.com

严干贵(1971—),男,通信作者,博士,教授,主要研究方向:新能源发电联网运行分析与控制技术。E-mail: yangg@neepu.edu.cn

李泳霖(1993—),男,硕士研究生,主要研究方向:多光伏发电并联稳定性分析与控制技术。E-mail: liyonglin6633@126.com