求解饱和多孔介质圆柱壳动力学问题的一种半解析方法

向 宇， 孙 润， 陆 静， 袁丽芸

(1. 广西科技大学 汽车与交通学院，广西 柳州 545006； 2．广西汽车零部件与整车技术重点实验室(广西科技大学)，广西 柳州 545006)

由于饱和多孔介质板壳结构具有良好吸声、吸能性能，已广泛应用于航空航天、交通运输、土木建筑等领域。因此，自1956年Biot提出饱和多孔介质的振动和声传播经典理论以来[1-2]，一直备受国内外学者的关注[3-4]。在饱和多孔介质圆柱壳动力学问题的建模和求解方法上，Shah利用经典Biot理论，通过将固体骨架和内部流体的位移分量沿径向展开成Bessel函数、纵向展开成指数函数的乘积形式，分析了无限长充液多孔介质圆柱壳的轴对称振动问题[5]；Zhou等[6]通过模态展开方法描述壳体位移和声压，对敷设有多孔吸声材料的有限长双层圆柱壳的声透射问题进行了研究；Daneshjou等[7]将多孔介质层模拟为具有等效特性的流体，并将入射声压展开为Hankel函数，研究了多孔材料夹芯的双壁面圆柱壳体中声波的传播问题；Allard等[8]结合声波在介质中的传播理论，建立了饱和多孔介质材料声振特性分析的有限元模型；Boily等[9]采用有限元法对敷设有黏弹材料和多孔吸声材料的两端自由有限长圆柱壳的声振频响进行了分析；Liu等[10]也采用有限元法研究了梯度泡沫铝夹芯圆柱壳的动力响应和爆炸抵抗性能。然而。迄今为止对饱和多孔介质材料的模型简化多采用等效媒质法，应用较广泛的为Gaunaurd等[11]依据经典的散射原理提出的Gaunaurd法，即当固体骨架较软时，将其视为一种等效流体，而当固体骨架较硬时，则视其为一种等效的弹性介质。这些简化模型虽然比较便利，但由于忽略了固体骨架和内部流体间的耦合作用和能量耗散，其计算结果仅适用于低频段[12]。

本文从三维经典Biot理论出发，结合弹性板壳理论[13]，充分考虑固体骨架和内部流体间的耦合作用和能量耗散，建立了一种分析有限长饱和多孔介质圆柱壳声振特性的半解析方法。该方法可适用于任意边界条件，且在中高频段内也具有较高的计算精度和稳定性，可为多孔介质圆柱壳的动力学分析提供一种新的思路和方法。

1 饱和多孔介质圆柱壳控制方程的建立

如图1所示柱坐标系(x,θ,z)下的饱和多孔介质圆柱薄壳，壳的长度和厚度分别为L、h，中曲面半径为Rs。

图1 多孔介质圆柱薄壳示意图

1.1 饱和多孔介质圆柱壳的本构关系

根据Biot理论，柱坐标下三维多孔介质的应力-应变关系为

σi=2Nei+Ae+Qε

(1a)

τij=Neij

(1b)

(1c)

式中：σi(i=x,θ,z)表示沿x，θ和z三个方向固体骨架的正应力；ei,εi(i=x,θ,z)分别表示固体骨架和内部流体的三个正应变分量，τij,eij(i,j=x,θ,z)分别表示固体骨架的三个剪应力分量和相应的剪应变分量；e,ε分别表示固体骨架和内部流体的膨胀应变；Q为微元体发生形变时固体骨架和内部流体相互作用的有关参数；R表示微元体内与流体有关的压力参数；p为流体压力；φ为多孔介质孔隙率；N,A类似于均匀各向同性弹性体中的拉美系数。

由式(1c)中的第1式，得

(2)

将式(2)代入式(1a)可得：

(3)

当圆柱壳很薄时，根据薄壳理论的直法线假设，中面法线及其垂直线段之间的直角保持不变，这两个方向的切应变为零，即exz=0,eθz=0。而且，与中面平行的截面上的正应力的影响可以忽略不计，即σz-φp=0。将以上关系式代入式(3)的第3式，得

(4)

将式(4)回代入式(3)，并结合式(1a)、(1b)、(1c)，可得饱和多孔介质圆柱壳的本构关系如下

(5)

1.2 饱和多孔介质圆柱壳固体骨架的内力-位移关系

(6)

横截面沿x方向的转角θx可写为

(7)

根据圆柱壳的几何方程，并结合式(6)和式(7)，可导出多孔介质圆柱壳固体骨架的应变-位移关系

(8)

(9)

1.3 饱和多孔介质圆柱壳固体骨架的动力学方程

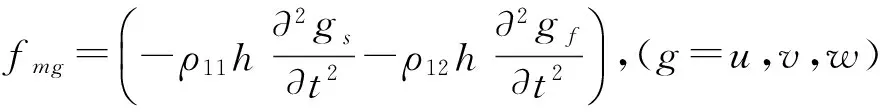
利用薄壳理论，可将Boit理论中多孔介质材料的三维运动方程简化为二维曲面坐标下多孔介质壳体固体骨架的动力学方程

(10)

式中：α和β表示曲面坐标，H1和H2分别表示两个方向的拉梅系数；Rα和Rβ分别表示中面沿两个方向的主曲率半径；Qα和Qβ表示中面沿两个方向的横向剪力；uf,vf,wf表示多孔材料中内部流体中曲面位移分量；ρ11=(1-φ)ρs+φ(α∞-1)ρf表示固体骨架相对密度；ρ12=-φ(α∞-1)ρf表示固体骨架与内部流相互作用产生的耦合质量密度；ρs表示固体骨架密度；ρf表示内部流体密度；α∞为多孔介质材料的扭曲率；b=ηφ2/q表示达西系数；η为流体黏度；q为达西渗透率。

对于圆柱壳，α=x,β=θ,H1=1,H2=Rs,Rα=∞,Rβ=Rs，将其代入式(10)，经整理后可得谐激励下多孔介质壳体固体骨架的运动方程

(11)

其中，Ω11=jωb-ρ11ω2，Ω12=jωb+ρ12ω2。

1.4 饱和多孔介质圆柱壳内部流体的运动方程和本构关系

不计流体自身黏性(pij=0,i≠j)，柱坐标下内部流体的运动方程为[14]

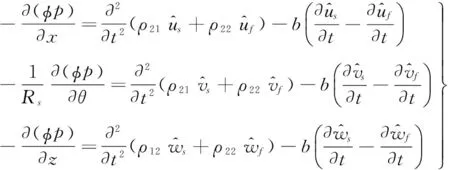
(12)

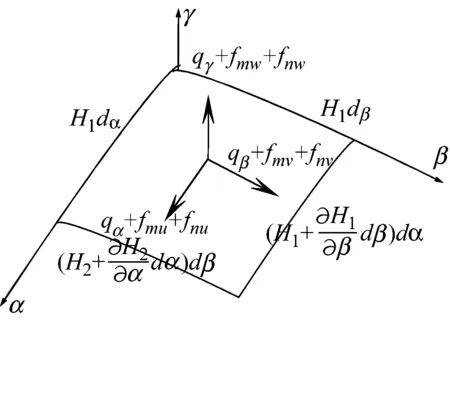
(a)

(b)

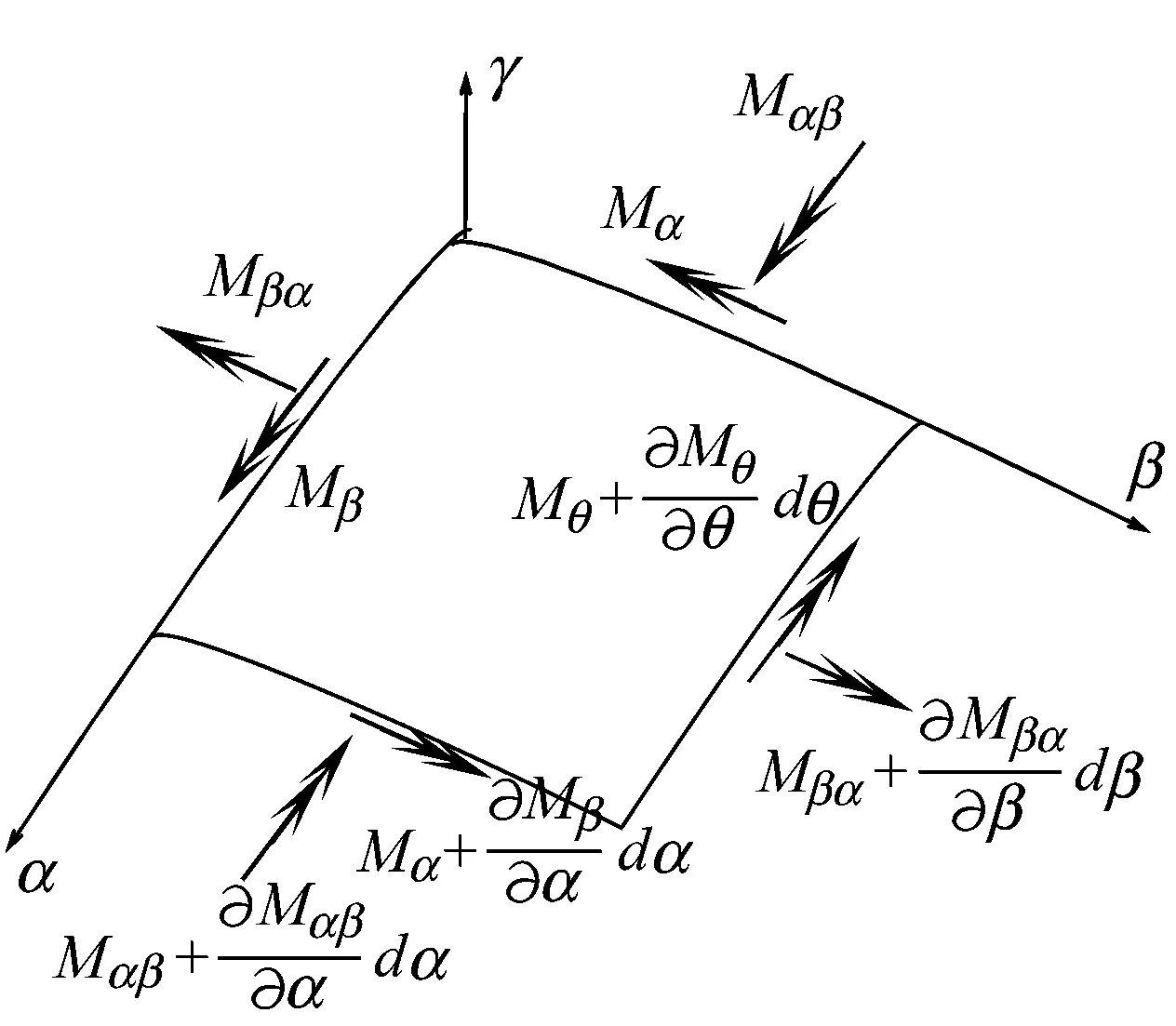
(c)

图2 圆柱壳中曲面微元的受力分析

Fig.2 The force analysis of mid-surface element in cylindrical shell

谐激励作用下，由式(12)可得内部流体任一点位移幅值为

(13)

式中：Ω21=bωj+ρ21ω2,Ω22=bωj-ρ22ω2。其中，ρ21=ρ12，ρ22=φρf+φρf(α∞-1)表示多孔介质内部流体的相对密度。

将式(6)代入式(13)，并沿厚度方向积分，可得流体的中面位移幅值

(14)

谐激励下，内部流体的应变-位移关系为

(15)

将式(13)的第3式代入式(15)的第3式，有

(16)

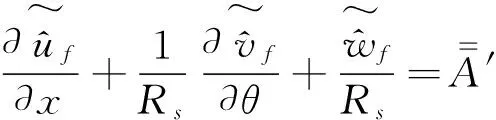
(17)

将式(8)、式(13)和式(14)代入式(17)，并将方程两边沿厚度z积分，得

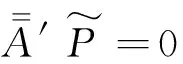
(18)

采用同样的方法将式(17)整理后乘以z，并沿厚度z积分，得

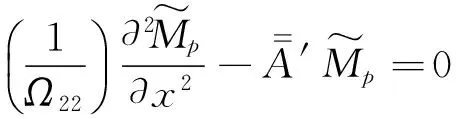
(19)

2 饱和多孔介质圆柱壳的一阶常微分矩阵控制方程

谐激励作用下，薄壳的Kelvin-Kirchhoff等效剪力为

(20)

根据圆柱壳的几何特性，可将频域内各物理量沿周向展开成Fourier级数，然后，对各物理量进行无量纲化，则上述变量可以写为

其中，kn表示周向波数，带“-”的变量表示为频域内各物理量环向Fourier级数展开后的无量纲状态量。为了便于书写，在下文中省略上标(n)。

通过整合式(7)、(9)、(11)、(14)、(18)、(19)、(20)，消去中间变量，推导过程详见附录Ⅰ,可得饱和多孔介质圆柱壳用12个状态分量表示的一阶常微分矩阵方程

(21)

根据本文作者近年来的研究，式(21)可采用齐次扩容精细积分法和精细元法进行高精度求解[15]。将待求圆柱壳沿轴向划分为M个单元，在每个单元内设置一定的精细积分步数，由齐次扩容精细积分法求出每个单元两端点(节点)处状态向量的关系如下

-Ti·Zi-1+Zi=Qi(i=1，…，M)

(22)

则对于M个单元，可得到M个形如上式的关系式，合并写成矩阵形式

ΤΖ=Q

(23)

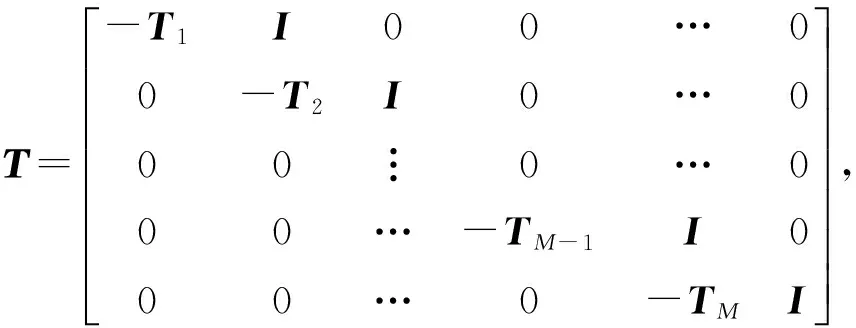
式(23)含12M个方程，12(M+1)个未知量。将圆柱壳两端处各6个给定的边界条件(4个骨架边界条件，2个内部流体边界条件)合并入上式，得到12(M+1)个方程，可解出12(M+1)个未知量。一旦解出各节点处的状态向量，壳体内任意点的状态向量即可再采用齐次扩容精细积分法求得。

对于自由振动问题，Q为零向量，将边界条件扩充到式(23)后，令其系数矩阵的行列式为零，可得固有频率的特征方程，从而得到结构振动的固有频率ω。由于计及了流固耦合作用，该频率为一复特征频率。定义损耗因子为：η=lm(ω)/Re(ω)。

3 算例分析

算例1当孔隙度趋向于零时，饱和多孔圆柱壳可近似视为一个各向同性的均匀弹性实体。考虑一个悬臂圆柱壳，取孔隙度φ=0.000 1，几何参数为：h=0.01 m，L=0.2 m，Rs=0.1 m，杨氏模量E=3.8×108Pa，泊松比μ=0.30，骨架材料密度ρs=2 700 kg/m3，内部流体为空气。采用本文模型和方法计算结构的固有频率，并采用有限元软件模拟与其等效的均匀弹性体，其固有频率的计算结果如表1所示。

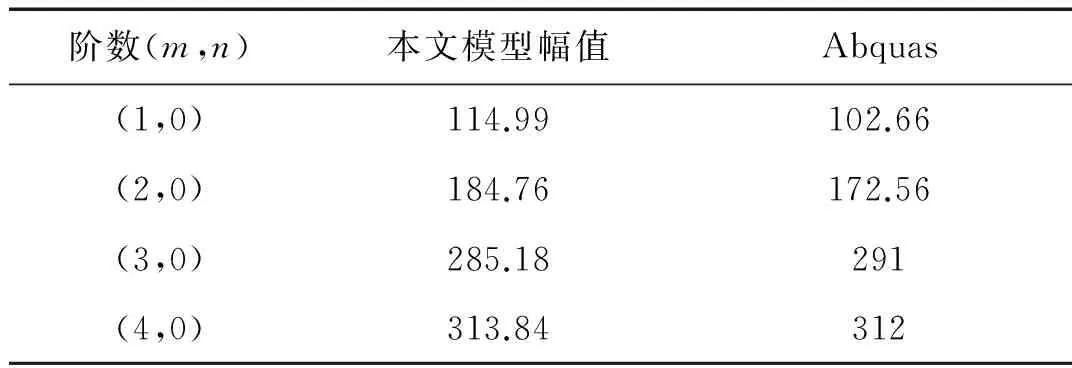
表1 固有频率计算结果对照

由表1可以看出，两种模型所得结果基本一致，说明了本文模型的正确性。

算例2为了进一步验证本文模型的精度，令孔隙度φ=0.8，壳的其他参数及边界条件同算例1，将本文方法与等效媒质法进行比较。在等效媒质法中，均质圆柱壳的等效弹性模量和密度分别为Ee=3.8×108Pa，ρe=541 kg/m3。表2分别给出了两种模型计算所得固有频率。其中，等效媒质法将结构视为一等效实体模型，可采用有限元软件计算，所得结构固有频率为一实数；由于本文模型计及了多孔介质内部流体和骨架的耗散作用，所得结构固有频率为一复数。

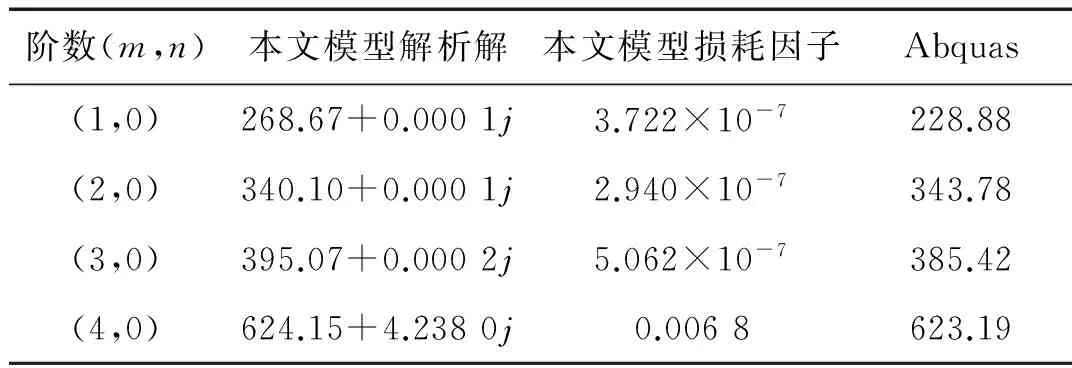
表2 本文模型与Abquas模型计算结果对照

从表2中可看出，两种模型所得固有频率幅值大体相当。但由于忽略了其内部流体的黏性影响，将结构视为一个等效实体模型，等效媒质法无法计及多孔介质结构的损耗特性，仅适用于骨架较硬，孔隙率较小，耦合影响不大的结构。而本文所提出的模型充分考虑了流体和固体的相互作用，不仅可以分析模型的损耗特性，且具有更为广泛的适用性。

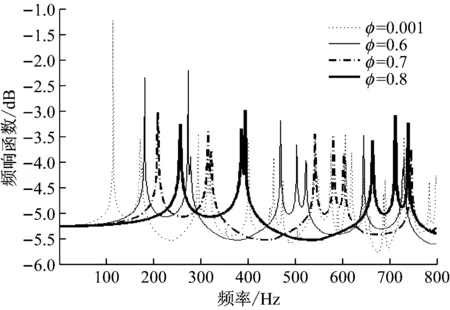
图3 孔隙率变化时多孔介质圆柱壳频响曲线对比

由图3可看出，随着孔隙率的增加，多孔介质圆柱壳的固有频率在逐渐增大，共振频率点处的峰值略有下降。因为孔隙率增大时，多孔介质结构的等效质量下降的速度比等效刚度快，从而导致结构的固有频率增大；同时，结构的耗散性能随孔隙率增大而更佳，导致共振频率点处的峰值下降。

4 结 论

基于弹性薄壳理论和经典Biot理论，本文建立了求解饱和多孔介质圆柱壳振动问题的半解析方法。由于充分考虑了多孔骨架和内部流体的耦合作用，且对流体位移的表达未做任何简化假设，本文方法可用于各种流体、激励和边界条件等，还可适用于较宽的频率范围，弥补了现有的等效媒质法等方法在分析饱和多孔介质圆柱壳动力学特性方面的不足。数值算例证明了本文方法的正确性。同时，数值计算表明，随着孔隙率的增加，多孔介质圆柱壳的阻尼特性将更佳。

附录Ⅰ控制方程的推导过程

1 基本方程

将式(7)周向展开并无量纲化后可得

(A1)

将式(9)周向展开并无量纲化后可得

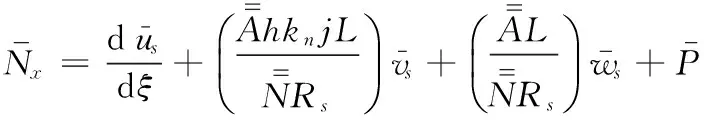
(A2)

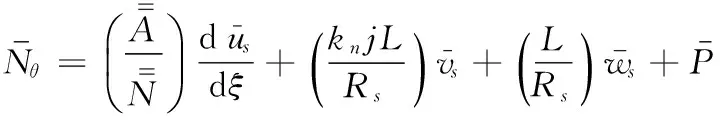
(A3)

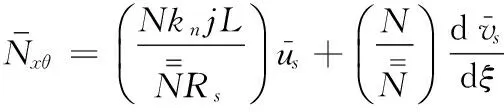
(A4)

(A5)

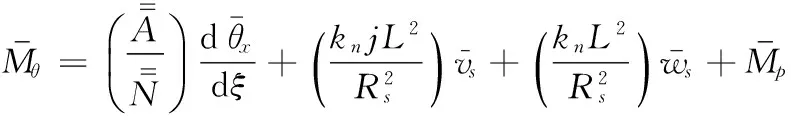
(A6)

(A7)

将式(14)代入式(11)后周向展开并无量纲化可得

(A8)

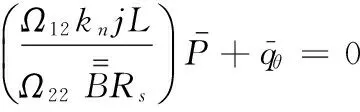
(A9)

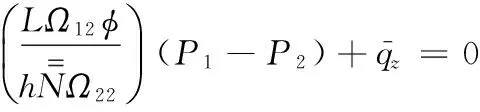
(A10)

(A11)

(A12)

式(18)和式(19)周向展开并无量纲化后可得

(A13)

(A14)

式(20)周向展开并无量纲化后可得

(A15)

(A16)

2 一阶常微分方程组的推导过程

由式(A2)可得

(A17)

由式(A4)、(A7)和(A15)可得：

(A18)

由式(A1)可得

(A19)

由式(A5)可得

(A20)

由式(A4)和式(A8)可得

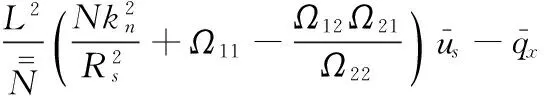
(A21)

由式(A15)、(A9)、(A11)、(A3)和(A6)可得

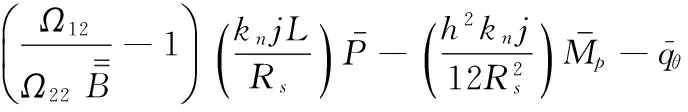
(A22)

由整合式(A16)、式(A10)、式(A11)、式(A3)以及式(A6)可得

(A23)

由式(A16)、式(A12)以及式(A7)可得

(A24)

由式(A13)可得

(A25)

由式(A14)可得

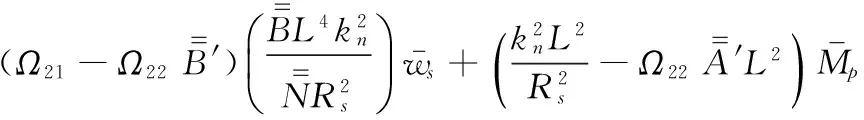
(A26)

附录Ⅱ系数矩阵[A]、[B]和向量{F}中的非零向量

1 系数矩阵A中的非零元素为

2 系数矩阵B中的非零元素为

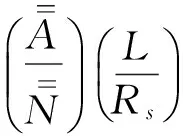
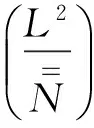
3 载荷向量中的非零元素为

[1] BOIT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid.Ⅰ.low-frequency range[J]. J Acoust Soc Am, 1956, 28(2):168-178.

[2] BOIT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid.Ⅱ.Higher-frequency range[J]. J Acoust Soc Am, 1956, 28(2):179-191.

[3] 刘志军,夏唐代,黄睿，等. Biot理论与修正的Biot理论比较及讨论[J].振动与冲击，2015,34(4):148-152.

LIU Zhijun, XIA Tangdai, HUANG Rui, et al. Compare and discussion for Biot theory and modified Biot one[J]. Journal of Vibration and Shock, 2015, 34(4):148-152.

[4] 敬霖, 王志华, 赵隆茂. 多孔金属及其夹芯结构力学性能的研究进展[J]. 力学与实践, 2015, 37(1):1-24.

JING Lin, WANG Zhihua, ZHAO Longmao. Advances in studies of the mechanical performance of cellular metals and related sandwich structures[J]. Mechanics in Engineering, 2015, 37(1): 1-24.

[5] SHAH S A. Axially symmetric vibrations of fluid-filled poroelastic circular cylindrical shells[J]. Journal of Sound and Vibration, 2008, 318(1/2):389-405.

[6] ZHOU J, BHASKAR A, ZHANG X. Sound transmission through double cylindrical shells lined with porous material under turbulent boundary layer excitation[J]. Journal of Sound and Vibration, 2015, 357:253-268.

[7] DANESHJOU K, RAMEZANI H, TALEBITOOTI R. Wave transmission through laminated composite double-walled cylindrical shell lined with porous materials[J]. Applied Mathematics & Mechanics, 2011, 32(6):701-718.

[8] ALLARD J F, ATALLA N. Propagation of sound in porous media: modelling sound absorbing materials[M]. New York: John Wiley &Sons, Ltd, 2009.

[9] BOILY S, CHARRON F. The vibroacoustic response of a cylindrical shell structure with viscoelastic and poroelasticmaterials[J]. Applied Acoustics, 1999, 58(2): 131-152.

[10] LIU X, TIAN X, LU T J, et al. Blast resistance of sandwich-walled hollow cylinders with graded metallic foam cores[J]. Composite Structures, 2012, 94(8):2485-2493.

[11] GAUNAURD G C, WERTMAN W. Comparison of effective medium theories for inhomogeneous continua[J]. Journal of the Acoustical Society of America, 1989, 85(2):541-554.

[12] 秦波, 梁彬, 朱哲民,等. 含气泡弱可压缩弹性材料的等效媒质法[J]. 声学学报, 2007, 32(2):110-115.

QIN Bo, LIANG Bin, ZHU Zhemin, et al. Effective medium method of slightly compressible elastic media permeated with air-filled bubbles[J]. Acta Acustica, 2007, 32(2):110-115.

[13] 曹志远.板壳振动理论[M].北京：中国铁道出版社,1989.

[14] 吴望一.流体力学(上册)[M].北京：北京大学出版社, 1983.

[15] NI Q, XIANG Y, HUANG Y, et al. Modeling and dynamics analysis of shells of revolution by partially active constrained layer damping treatment[J].Journal of Solid Mechanics, 2013, 5(5):468-479.