冲击载荷对铁路轴箱轴承塑料保持架动态性能影响研究

黄运生， 邓四二,2,， 张文虎， 胡 洁，， 孙立明, 马子魁

(1.河南科技大学 机电工程学院，河南 洛阳 471003； 2.辽宁重大装备制造协同创新中心,辽宁 大连 116024；3.西北工业大学 机电工程学院，西安 710071； 4.洛阳轴承研究所，河南 洛阳 470123)

在列车正常运行过程中由于车轮外圆擦伤、道岔轨面剥离等因素，车轮会承受到较大的冲击与振动，而轴箱轴承是与轮轴直接相连并把车轮转动转化成车体平动的关键构件，除了承受一系悬挂之上构架以及车体的重量还要承受轮轴带来的冲击载荷。近年来塑钢保持架[1]开始取代金属保持架应用在铁路轴箱轴承里。由于铁路线路工况复杂多变引起的保持架断裂会造成轴承卡死，将导致抱轴、热轴事故，已直接威胁到列车行车的安全。

轴承保持架在轴承内属于浮动件，对其单独进行动力学特性分析时的边界条件很难准确确定，一般采用拟动力学分析模型[2]，结合润滑理论对保持架运动特性和动力特性进行分析。Gupta[3]研究了保持架兜孔间隙和引导间隙等对保持架运转稳定性的影响。周延泽等[4]采用有限元的方法对高速轴承保持架的断裂失效原因进行了分析。Takafumi等[5]开发了能考虑接触区润滑油温升对保持架打滑率影响的方法，分析了轴承载荷、转速、供油率对保持架打滑率的影响。李晌等[6]采用刚柔耦合的方法结合动力学对保持架进行运动、受力以及变形的分析。邓四二等[7]对高速圆柱滚子轴承进行动力学分析，研究了保持架参数和轴承工况对保持架稳定性的影响。Ye等[8]建立了考虑套圈轴向倾斜圆柱滚子轴承仿真方法，分析内圈倾斜角对保持架涡动的影响。姚廷强等[9]对圆柱滚子轴承转速及径向力对保持架运行稳定性进行了分析。上述轴承保持架动态特性分析均基于轴承稳定运行工况条件下的进行的，对于非稳态变工况下[10-11]轴承保持架动态特性分析研究较少。在轴承实际使用中，非稳态变工况尤其冲击载荷对轴承保持架损伤影响更严重，例如对于机车轴箱轴承，在冲击载荷下，保持架可能发生直接断裂。鉴于此，本文在考虑列车车轮扁疤产生的轮轨冲击动力学特性的基础上，采用刚柔耦合的离散单元法，建立含冲击载荷的保持架非线性动力学分析模型，对冲击载荷与保持架动态特性的关系进行了分析。该研究为铁路轴箱轴承塑料保持架的结构优化设计提供理论依据。

1 轴箱轴承动力学模型建立

1.1 车辆系统扁疤冲击简化模型

一般冲击载荷指的是很短的时间内以较高的速度施加在构件上的载荷，属于动载荷，实际中在轴箱上安装加速度传感器，通过测得振动加速度的幅值大小和频率间接反映冲击的强弱。

对于高速行驶的列车，车轮扁疤引起的冲击属于轮轨系统激励中典型的脉冲型激扰[12]。车轮扁疤引起的周期性车轮与轨道之间的碰撞冲击，一方面碰撞冲击产生的垂向分量给轴箱使用的双列圆柱滚子轴承造成较大的冲击载荷，另一方面对轨道也造成较大损伤，给钢筋混凝土轨枕强度带来难以料想的伤害。

如图1所示，平面惯性坐标系S={Oi,Xi,Yi,Zi}固定在轴承上，坐标系S的原点Oi设在外圈的圆心上，Xi轴与轴承中心线重合，Zi为列车系统的垂向方向，Yi为车体前进的纵向。设车轮半径为R，假设在车轮的AB段处有一个扁疤，车轮扁疤长度为2d，车轮以A点为中心转动到B点处，将在B处发生碰撞，在垂向方向上车轮会以碰撞之后的初速度向上做减速运动，减速运动的加速度为a，随后回到车轮质心初始位置。在此过程中内圈跟随轮轴质心先下降后上升，碰撞发生的时间极短，由于轴箱上方一系悬挂力的作用使得轴承外圈来不及向上运动，造成轴承内圈相对于轴箱轴承外圈发生较大位移，轴承内部承受较大的冲击载荷[13]。

假设在B点碰撞时车轮和轨道之间不发生切向摩擦，碰前车轮质心Oi速度为V1，其角速度ω1=V1/R；碰撞时恢复系数为e，碰撞后车轮质心Oi切向速度为V2t、垂向速度为V2n，角速度ω2，B点车轮受到的切向冲量为St、法向冲量为Sn，一系弹簧簧下质量(轮轴)为Md，一系弹簧簧上质量(构架和车体)为Mu，轮对绕中心轴转动惯量为Jc，可得碰撞时的冲量方程及冲量矩方程：

Md(V2t-V1cosα)=St

(1)

Md(V2n+V1sinα)=Sn

(2)

-Jc(ω2-ω1)=R(Stcosα+Snsinα)

(3)

由恢复系数定义可知：

(4)

V2t-Rω2cosα=0

(5)

综合式(1)～(5)可得

(6)

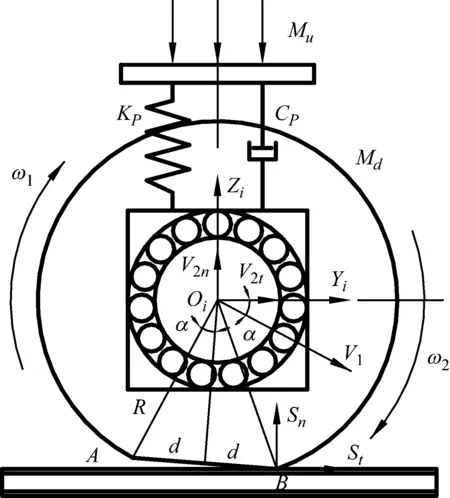
图1 车轮扁疤与轨道碰撞瞬间

轮对在碰撞之后以较大的反向速度V2n向上运动，由于受到簧上载荷和悬挂力的作用，车轮质心Oi很快回到垂向方向初始位置。由一系悬挂参数可以近似得到车轮垂向减速时加速度

(7)

式中:Fs=2KpΔSp+2CpΔVp，为整个车轮对承受的悬挂力，由一系弹簧力和阻尼力组成，该力随着轮对与构架之间的相对运动在变化，需要通过车系统多体动力学仿真的方法获取;Kp、Cp为单个轮子一系悬挂刚度和阻尼;ΔSp、ΔVp分别为车轮与构架间垂向相对位移和相对速度。

车轮与轨道之间碰撞的时间较短，一般在10-3～10-4s，如果将该碰撞瞬间看成匀加速运动，经估算车轮在垂向方向产生的位移极小故可忽略。假设轮轨碰撞之后的瞬间ΔSp变化为零，2KpΔSp=Mug，ΔVp=V2n，式(7)变为

(8)

假设车轮扁疤长度d为150 mm，车速150 km/h，将其他参数代入式(8)中，可得加速度a约为45g。带入不同的扁疤长度和车速可得到冲击加速度随两者的变化。

由图2和图3可知,随着车速的增加、扁疤尺寸的增大，冲击加速度也在增加[14]。由于该碰撞后的减速过程作用时间和作用力难以准确确定，本文将该冲击过程对轴箱轴承产生的响应模拟成短时间内轴承内圈垂向位移变化(如图4)，并假定冲击过程加速度恒定，分别计算不同的冲击加速度和冲击作用时间对轴承保持架的影响。

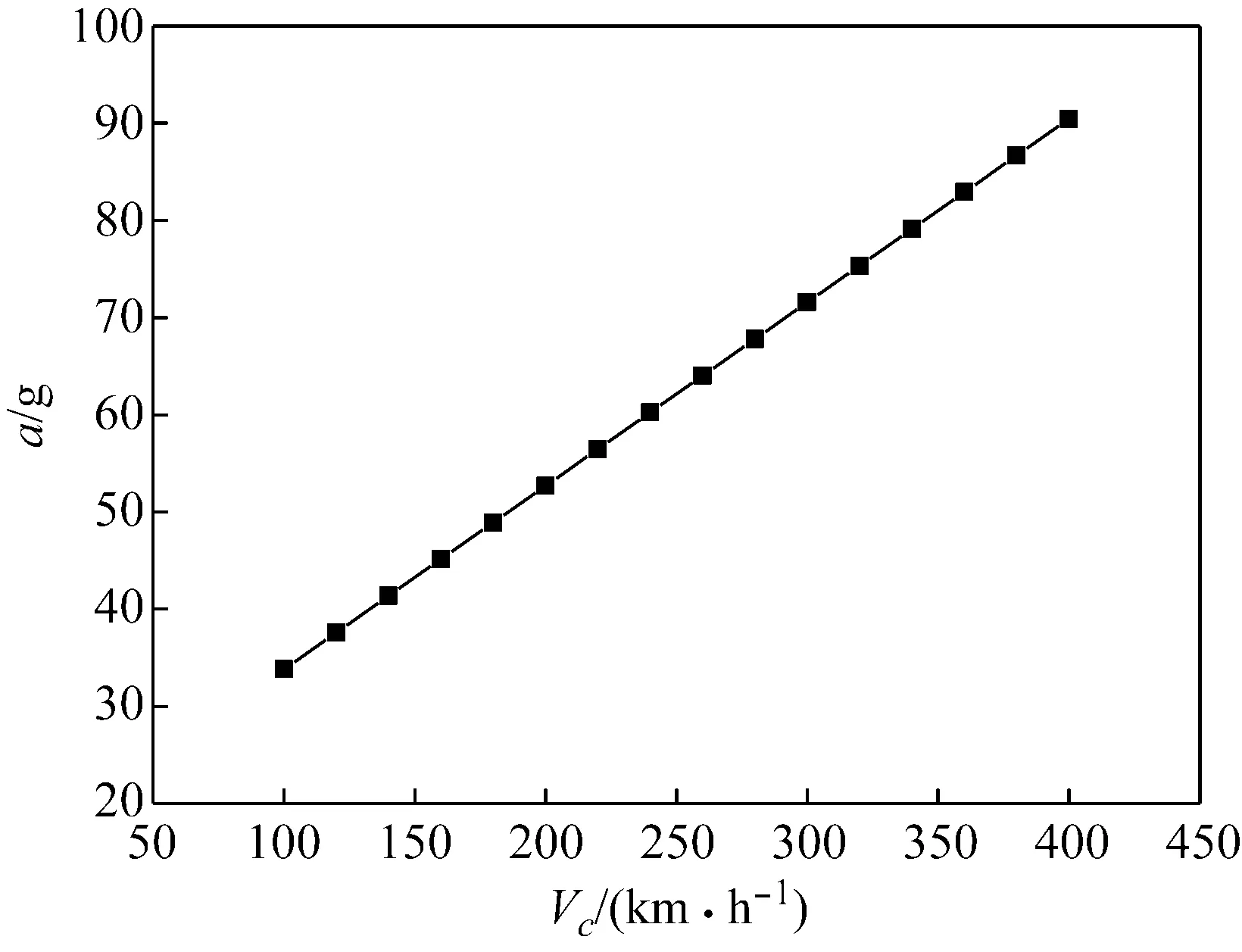
图2 扁疤长度150 mm时轮轴冲击加速度随车速的变化

Fig.2 The wheel impact acceleration varies with the train speed when wheel flat is 150 mm

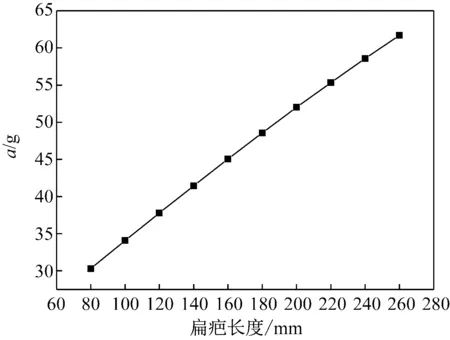
图3 车速为150 km/h时轮轴冲击加速度随扁疤长度的变化

Fig.3 The wheel impact acceleration varies with the wheel flat length when train speed is 150 km/h

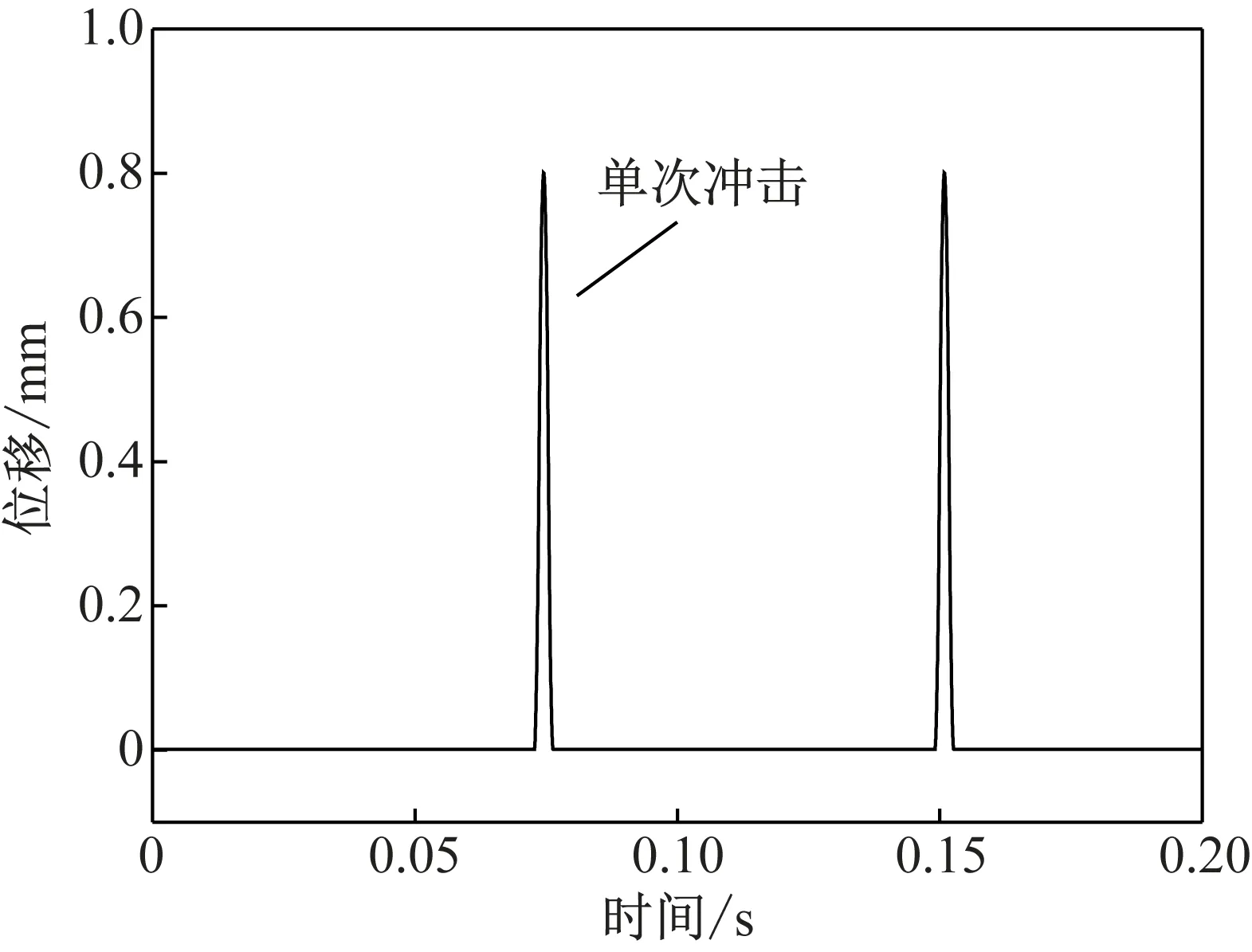
图4 轴承内圈垂向位移

1.2 轴承各部件自由度及主参数

为了便于分析和简化计算，本文分析双列圆柱滚子轴承各零件的自由度假设如表1所示。轴承承受的稳态外部载荷为径向载荷，大小为121 kN。保持架材料为TVP塑料保持架。单列滚子数18个。

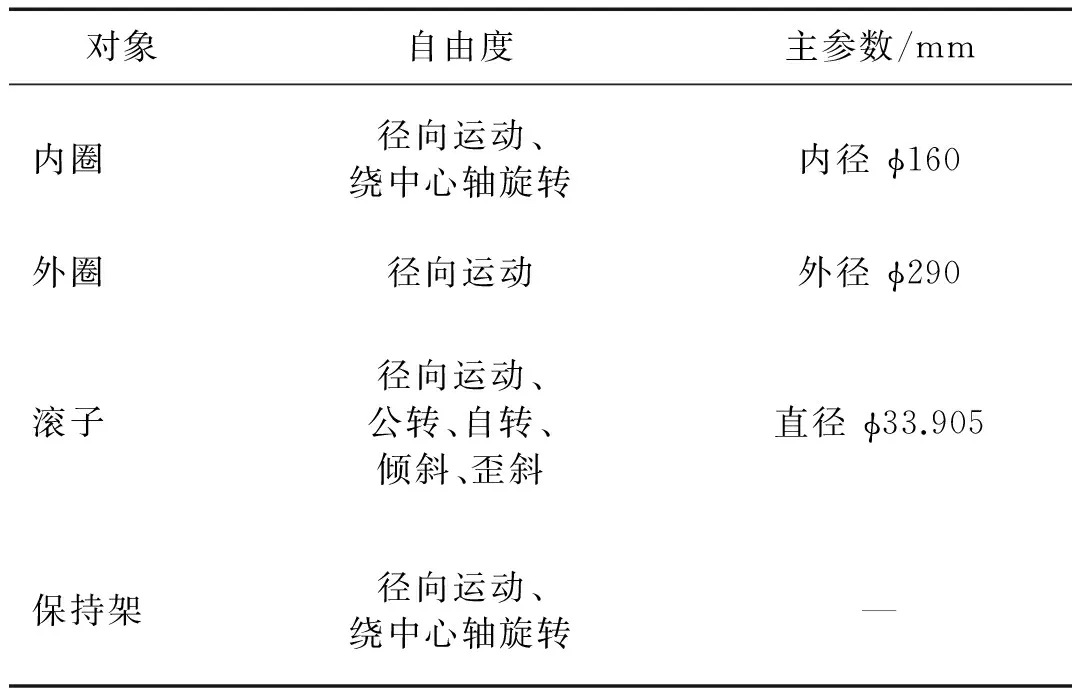
表1 轴承各部件自由度及主参数

1.3 滚子与保持架兜孔作用力模型

如图5中主要在兜孔坐标系(Xp,Yp,Zp)内描述滚子与保持架之间的运动及受力关系。创建柔性保持架[15]的具体方法是沿保持架相邻两兜孔中心截取使得保持架兜孔变成离散刚体，两刚性过梁之间通过弹簧和阻尼进行连接，通过有限元模型选取兜孔中心处在轴承径向平面内的刚度和阻尼矩阵作为每个离散刚性单元之间连接的输入。当滚子与过梁发生碰撞时，两者会产生局部弹性变形，促使保持架发生平移和转动，相邻过梁之间经过力的作用会发生移动。如此可以从基于Hertz理论的局部弹性变形转化到保持架的整体变形和运动。

保持架转速与滚子公转速度存在差异而产生的滚子表面与保持架兜孔的接触变形，形成的主要作用力有法向作用力Fcn、接触切向力Fbτ，如图5所示。

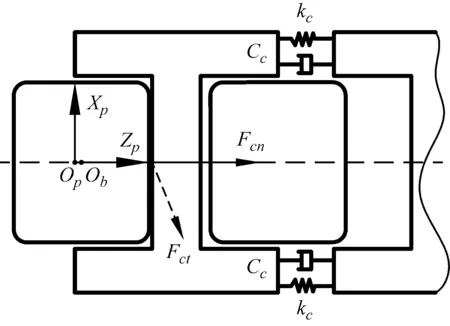
图5 滚子与保持架兜孔作用模型

考虑到滚子与保持架兜孔的接触处黏滞阻尼作用，保持架受到的法向接触力为[16]

(9)

接触处的切向摩擦作用力为

Fcτ=μFcn

(10)

式中，因为保持架表面较为粗糙，μ取边界摩擦因数[18]。μ=(-0.1+22.28s)e-181.46+0.1，s为接触处的滑滚比。

1.4 保持架和引导套圈之间作用力

本文研究的轴承保持架引导方式为外圈引导，对于润滑剂作用的轴承，当轴承高速运转时，在套圈引导面与保持架外柱面之间讲产生流体动压力，作用模型类似于短滑动轴承。如图6所示，保持架与套圈接触平面坐标系Sc={Oc,Yc,Zc}固定在保持架上，坐标系Sc的圆心Oc在保持架的圆心上，Zc轴正好通过最小油膜h所在的点，相对于惯性坐标轴Zi，Zc转动了ψ角。

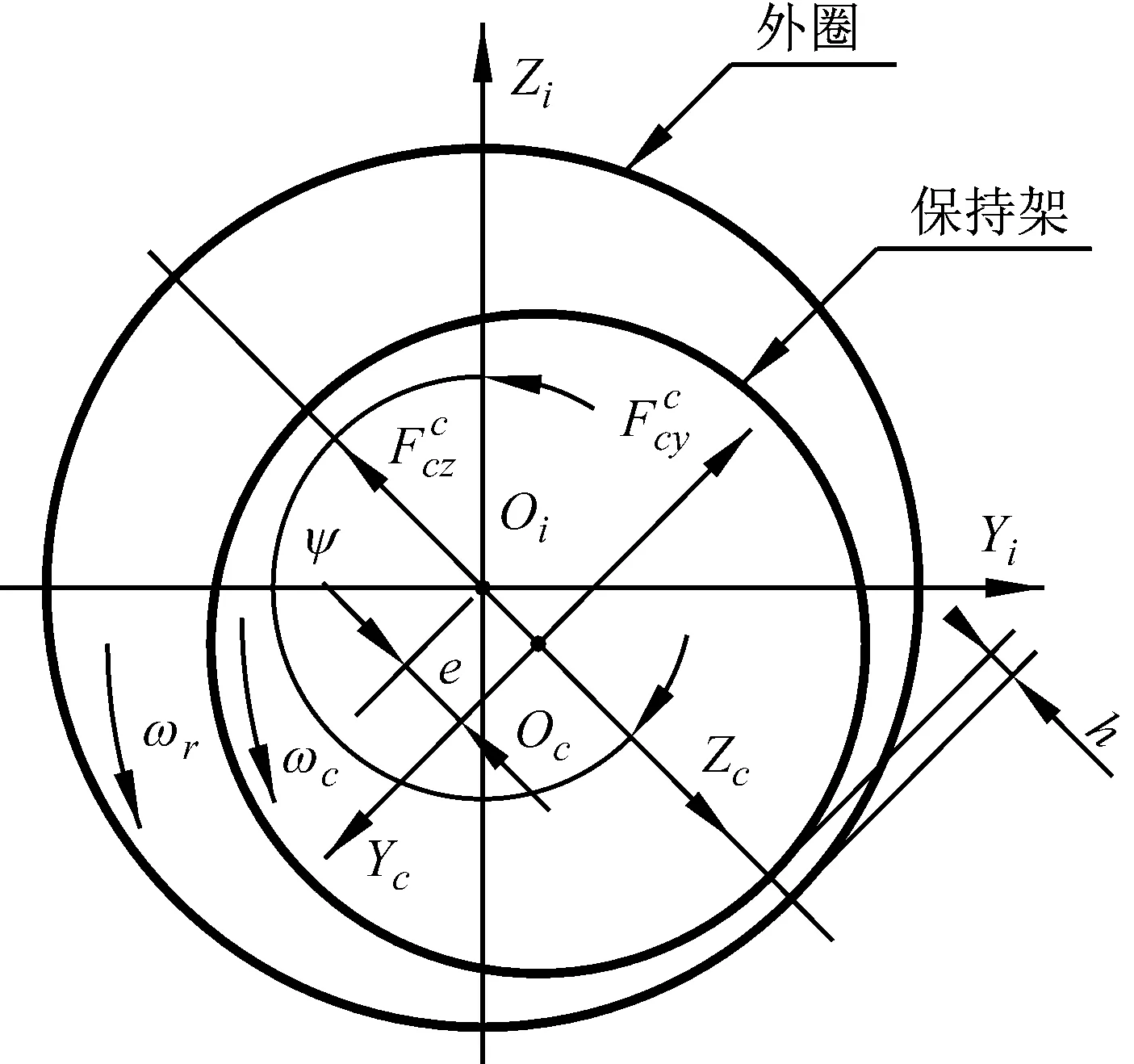
图6 保持架与外圈作用模型

保持架与套圈引导面之间的最小油膜为

h=Cg-e

(11)

式中:Cg为保持架引导间隙;e为保持架圆心相对于轴承外圈圆心的偏心距。

考虑润滑油及表面粗糙度等因素，两者之间接触状态分为两种，当h大于或等于某一临界值Δr时，保持架与外圈引导面之间为流体动压润滑状态，否者视为Hertz接触状态。

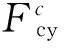
(12)

(13)

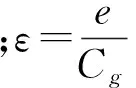
流体动压油膜的分布压力会对保持架表面产生摩擦力矩

(14)

式中:ν=Rgc(ωr-ωc)为引导面与定心面相对滑动速度。

当h<Δr时，保持架与外圈引导面将发生Hertz接触，接触法向作用力为

(15)

(16)

式中:Ecr为保持架与外圈的当量弹性模量；接触处的趋近量δcr=h-Δr；μrc为保持架与引导套圈之间边界摩擦系数，sign为取正负符号。

此时产生的力矩为

(17)

1.5 保持架运动微分平衡方程

(18)

(19)

(20)

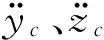
2 计算结果分析

2.1 刚、柔保持架与滚子作用力对比

由于该双列圆柱滚子轴承仅承受径向载荷，本文主要分析滚子与保持架过梁之间的碰撞作用力，如图按照柔性保持架的建模方式，保持架是由多个刚性离散单元通过弹簧阻尼连接而成，每个离散单元(Segment)会受到相邻的两个滚子的作用力，如图7所示，例如与Segment 1(S1)直接作用的是Roller 1(R1)和Roller 18(R18)，Roller 18位于滚动方向的前方，Roller 1位于滚动方向的后方。

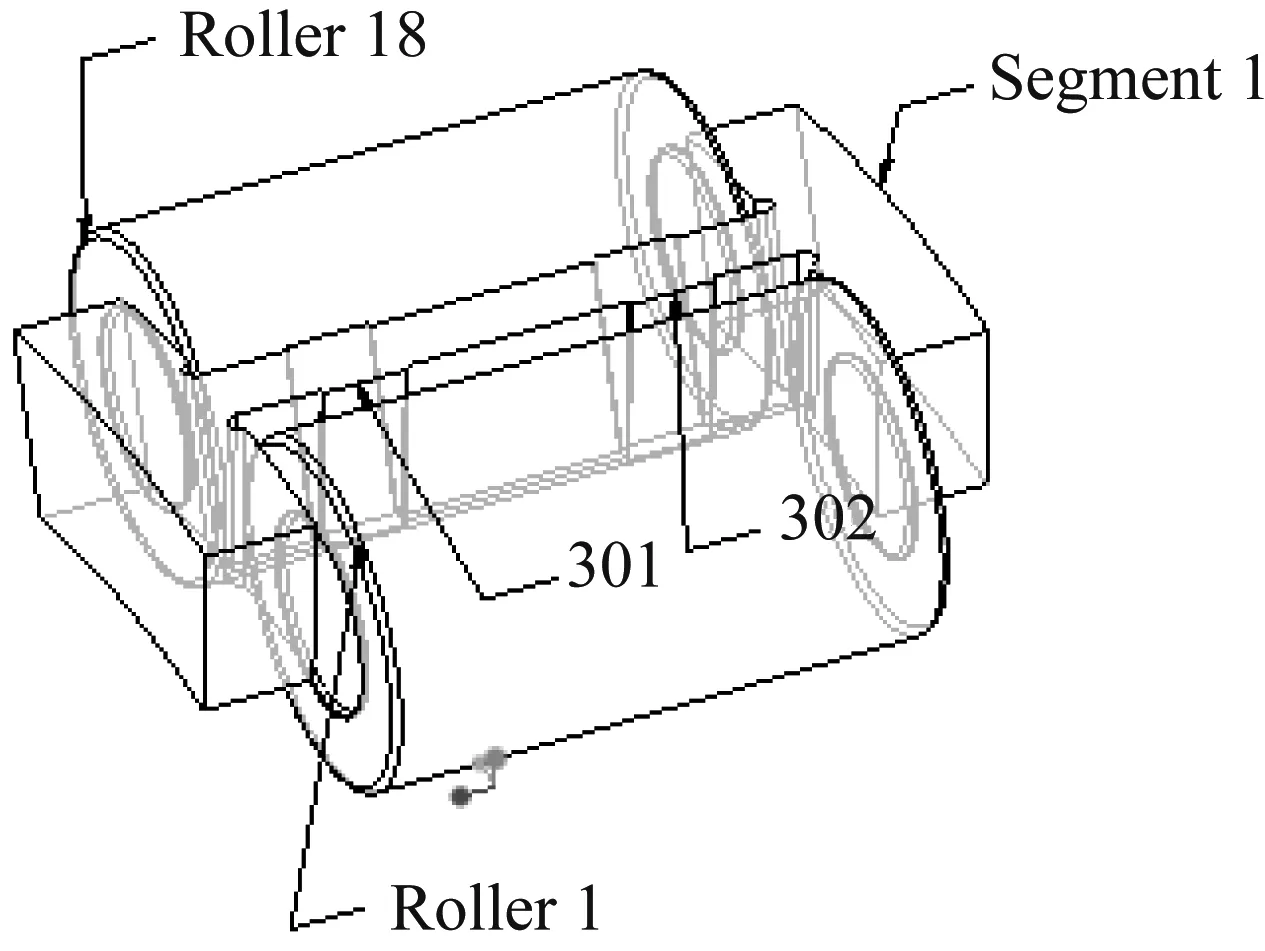
图7 单个过梁与相邻滚子位置关系

如表2可知，有冲击时滚子与保持架碰撞作用力比无冲击时大很多，说明外部冲击会较大程度上增大滚子与保持架的碰撞作用力。对比发现，柔性保持架要比刚性保持架碰撞力小得多，原因是保持架在受到滚动体及引导套圈的作用力之后，会发生整体变形，能较大的吸收碰撞能量，两者的碰撞作用力会因为保持架的变形小很多。实际应用中该轴箱轴承保持架为塑料保持架，那么利用柔性保持架分析受力会更加接近真实情况。

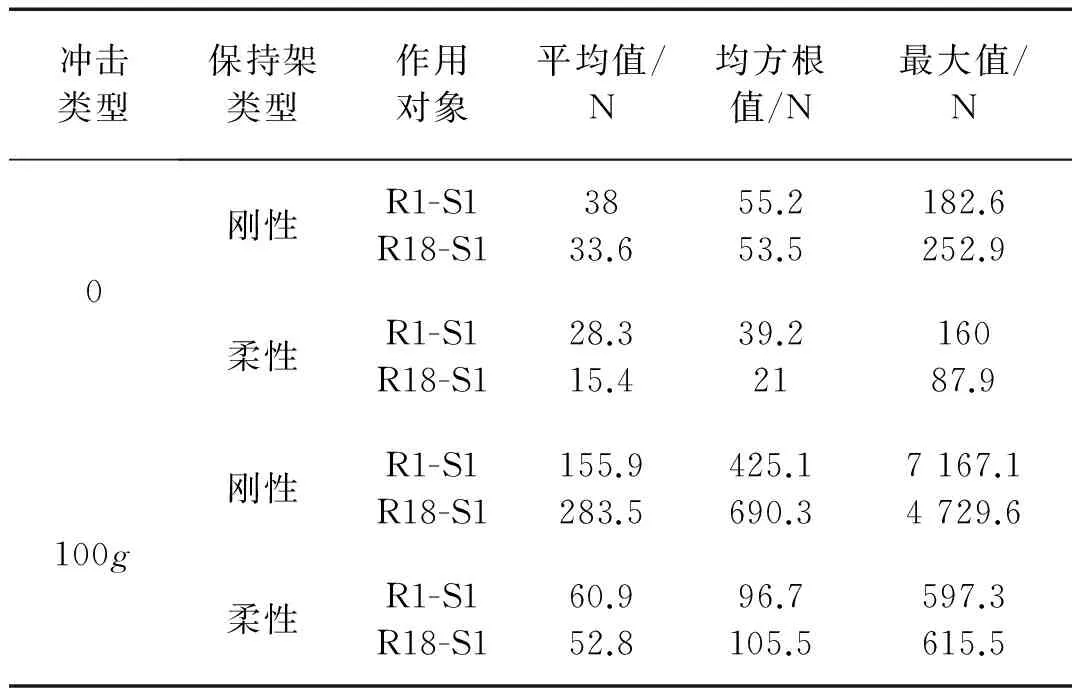
表2 有无冲击刚柔保持架与滚子碰撞力对比

通过保持架质心轨迹可以查看保持架的运动规律。由图8对比刚柔保持架质心轨迹可以看出，柔性保持架运动幅度要明显大于刚性保持架，Y向的运动幅度大约是刚性保持架的1.5倍。这种运动和变形会较大程度上吸收来自于滚子或者引导套圈的碰撞能量，比较符合真实情况。对比图8和图9可以看出对于柔性保持架在有冲击存在时，保持架在垂向(Z)方向上有较大位移产生，会导致保持架与引导套圈引导面之间的直接碰撞，说明冲击发生后会明显增大保持架的运行不平稳性。

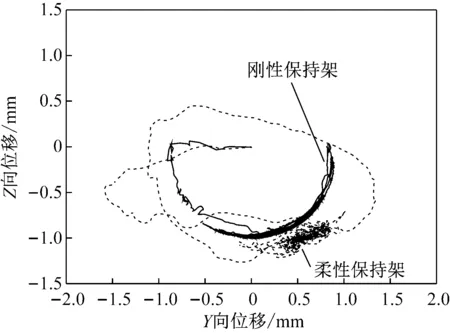
图8 无冲击时刚柔保持架总体质心轨迹

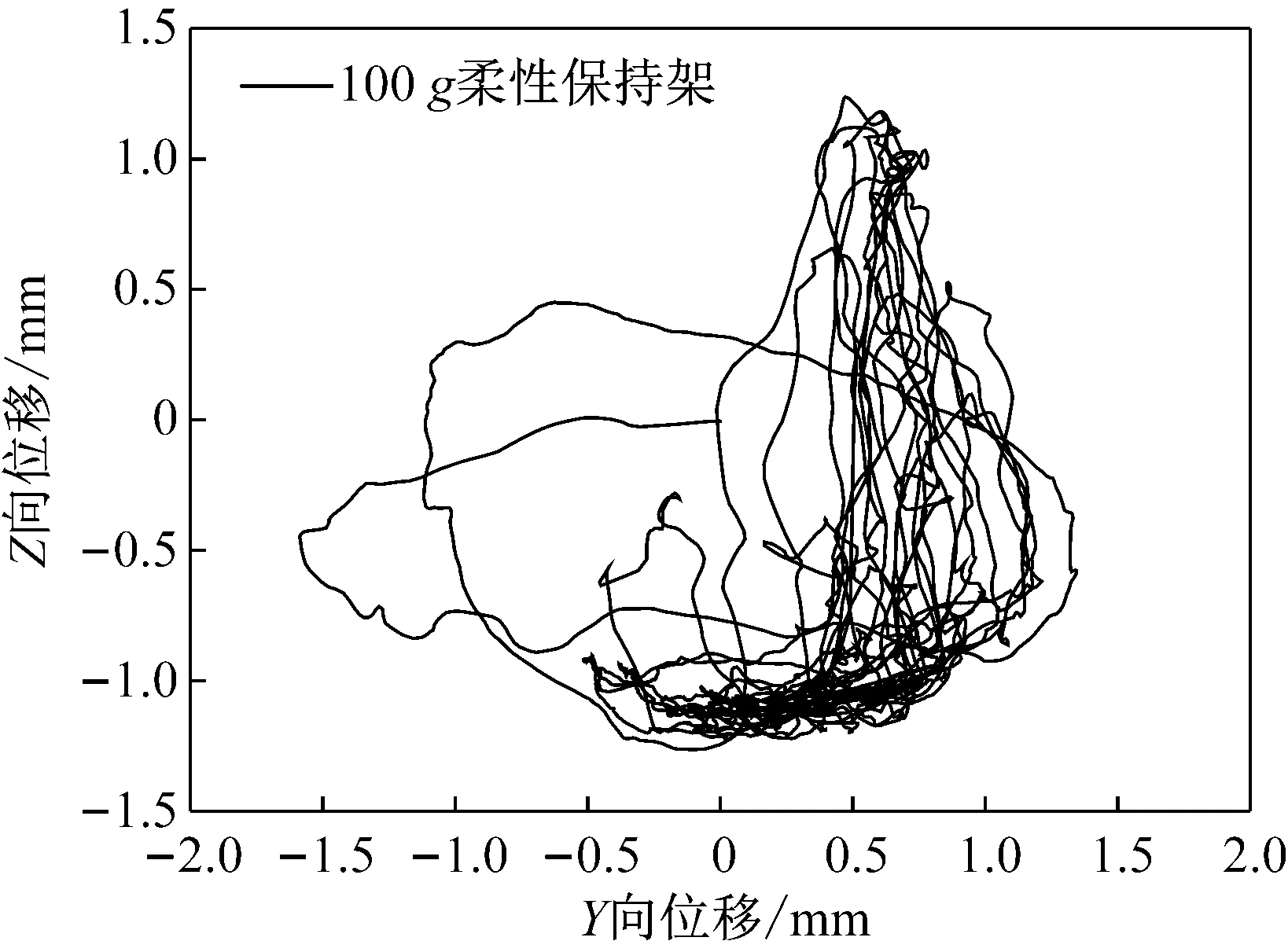
图9 有冲击发生时柔性保持架平均质心轨迹

2.2 无冲击时保持架与滚子之间动力学规律

当无外部冲击发生时，轴承仅仅承受稳定静态外载荷，内圈以某一转速匀速运转，带动滚子和保持架稳定运转。图10右侧坐标轴表示滚子与内圈滚道之间接触力，左侧坐标轴为滚子与保持架过梁作用力。可以看出，滚子在进入和离开承载区时会与保持架过梁发生随机碰撞，碰撞作用力与内圈和滚子之间接触力要小得多；滚子在承载区时，基本上没有碰撞力产生；在非承载区内，1号过梁主要受到来自于滚动方向前方的18号滚子的碰撞力，当滚子运动到出承载区的瞬间，1号过梁受到的碰撞力主要来自于滚动方向后方的1号滚子。

由图11所示，当滚子进入承载区时，滚子与内外滚道之间的间距越来越小，受到滚道的摩擦拖动作用增大，其自转速度迅速变大并稳定，公转速度变动较小，此时会对保持架过梁产生阻碍作用；在离开承载区的瞬间由于滚道拖动作用减小，滚子自转速度开始降低，其运动不稳定性增加，会产生对前后过梁的碰撞作用；在承载区的滚子与内外滚道之间基本上无打滑，公转速度与保持架一致，故基本没有碰撞作用力产生。

图10 无冲击时1号柔性过梁与相邻滚子之间碰撞力

Fig.10 Contact force between elastic cage bridge and adjacent rollers under no impact

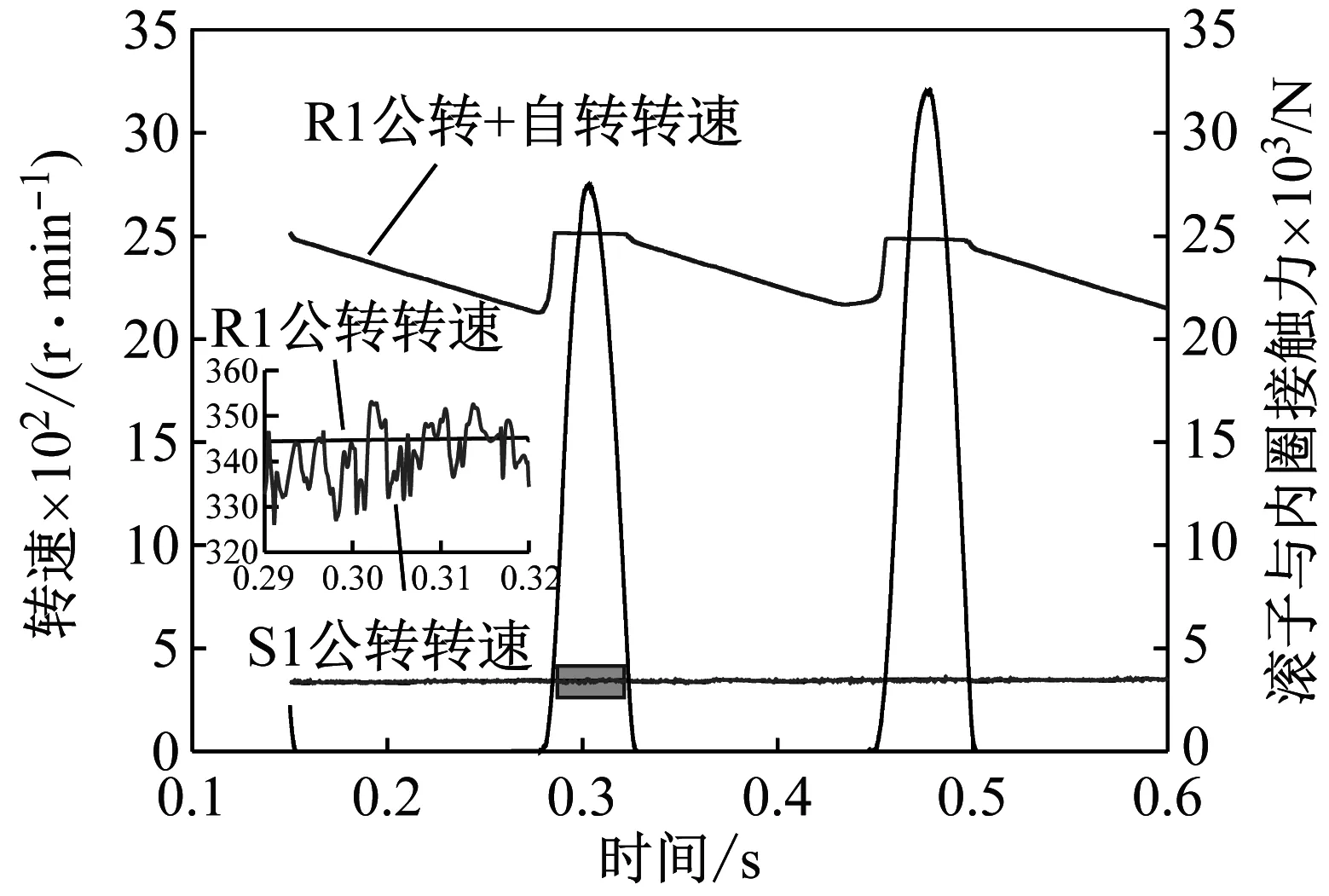
图11 无冲击时1号柔性过梁与1号滚子转速随时间变化

Fig.11 The speed of elastic cage bridge and adjacent roller varies with time under no impact

对于圆柱滚子轴承承受单一径向载荷，结合滚子和保持架的运动受力特性可得到两者之间碰撞力的分布规律特点：保持架由外圈引导时，在承载区两者基本上无碰撞作用；滚子在非承载区主要对保持架过梁有阻碍作用；滚子离开承载区时与保持架碰撞作用更显著。保持架受到滚子和引导套圈的作用力使其处于动态平衡状态。

2.3 有无冲击滚子与保持架之间作用力对比

轮轨技术一直是轨道交通领域的主流技术，其中轨道不平顺尤为复杂和关键，是车辆-轨道系统振动的主要激励源。轨道不平顺中短波成分和前述的车轮扁疤都是引起轮轨系统高频振动的主要原因，会降低轮轨以及直接相连的轴承的寿命。通过测得轴箱的加速度可以很大程度上反映出轨道短波不平顺，这种短波不平顺会产生较大的垂向轮轨力和冲击加速度[20]。本文旨在探究不同冲击加速度下，轴箱轴箱内部运动和受力特性，尤其对保持架断裂失效进行分析。分别计算了内圈垂向冲击加速度为0、100g、200g、400g、600g、800g时，滚子与保持架碰撞作用力。

滚子与保持架作用力属于随机碰撞接触力，由图12可以看出随冲击加速度的增加，滚子与保持架作用力会显著增加，单个过梁在冲击发生的时刻受到相邻的两个滚子碰撞力大小基本一致。当冲击加速度持续增加时滚子与保持架过梁平均碰撞力呈指数增加。保持架因为巨大的冲击发生整体变形和引导套圈接触，在冲击方向上滚子与保持架之间作用力会导致保持架过梁的直接断裂。

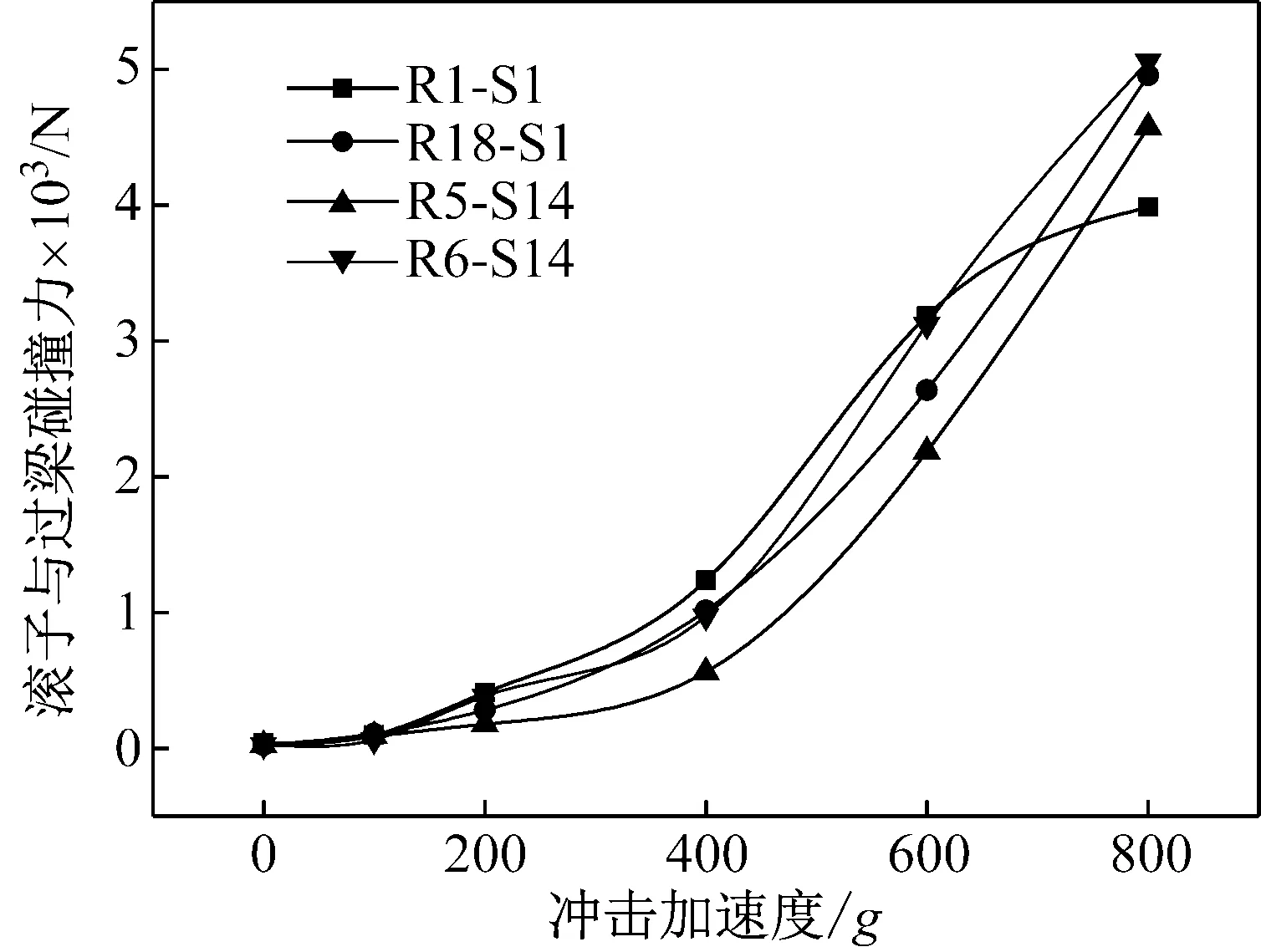
图12 过梁受到滚子的碰撞力RMS值随冲击加速度变化

Fig.12 Cage bridge and roller contact force RMS value varies with impact acceleration

由图13对不同冲击加速度下相同运转时间内滚子与保持架碰撞频数进行统计，可以看出不同大小碰撞作用力发生的频次，随着冲击加速度的增加碰撞几率也在大大增加，这样会大大增加保持架的疲劳速率。

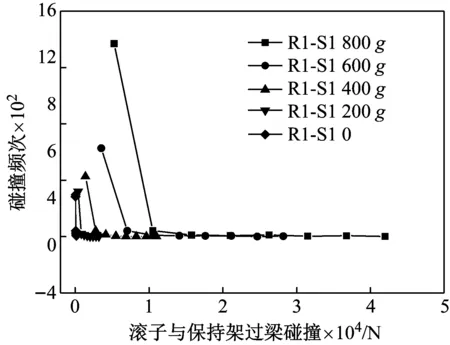
图13 不同冲击加速度下滚子与过梁碰撞力的频数统计

Fig.13 Cage bridge and roller contact force frequency statistics under different impact acceleration

基于2.2的分析结论，无冲击时保持架与滚子之间作用力分布规律处于一种动态平衡，而当垂向冲击发生时，内圈会带动滚子向上运动，处于承载区的滚子与保持架之间首先发生接触，滚子带动保持架向上运动，此时处于非承载区的滚子因为跟滚道之间拖动力不足由于惯性停留在原处，随后就产生了滚子与保持架过梁之间强烈的碰撞作用力。滚子与保持架过梁发生碰撞力方向一般是沿着绕轴承中心轴线的圆周方向，无冲击时因为两者间速度差产生碰撞力，而有冲击时速度差会显著增加，保持架断裂失效难以避免。

2.4 有无冲击保持架与外圈之间作用力对比

由图14可知冲击加速度为0时保持架与引导套圈之间作用力几乎为零。在冲击加速度逐渐增大时作用力呈指数上升。由于两者在引导面的接触点存在相对滑动速度，较大的接触作用力会产生较大的滑动摩擦，冲击加速度越大，产生的摩擦越严重。保持架与引导套圈之间连续不断碰撞摩擦会加速保持架引导面的磨损，一方面降低保持架侧梁的强度，另一方面这种冲击造成的磨损在保持架引导面上分布不均匀，会造成保持架质量中心与形心的不重合，更增加了保持架的运动不平稳性。

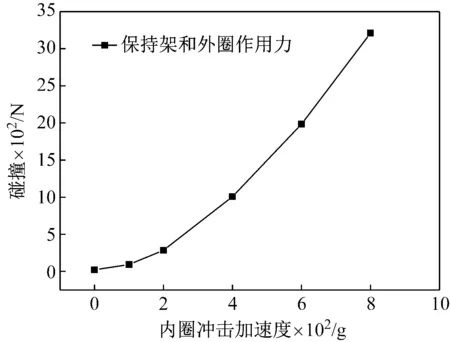
图14 保持架与外圈碰撞力随冲击加速度变化

Fig.14 Cage and outer ring contact force RMS value varies with impact acceleration

2.5 冲击作用时间对滚子与保持架之间的作用频数影响分析

本文对同一冲击加速度下不同冲击作用时间进行了对比计算，图15对碰撞频次进行统计，可以看出当作用时间成倍增加时，两者之间的碰撞几率大大增加，碰撞力平均值和最大值也在增加。冲击作用时间跟车辆的悬挂系统的刚度和阻尼有关系，当阻尼较大时，系统的耗能能力较强，会缩短冲击作用时间。本文分析的是扁疤造成的轮轨冲击对轴箱轴承的单次冲击，实际中伴随着悬挂系统对冲击能量的耗散，该冲击会引发短时间内的冲击振动，带来的滚子与保持架之间碰撞频次的增加引发疲劳失效。

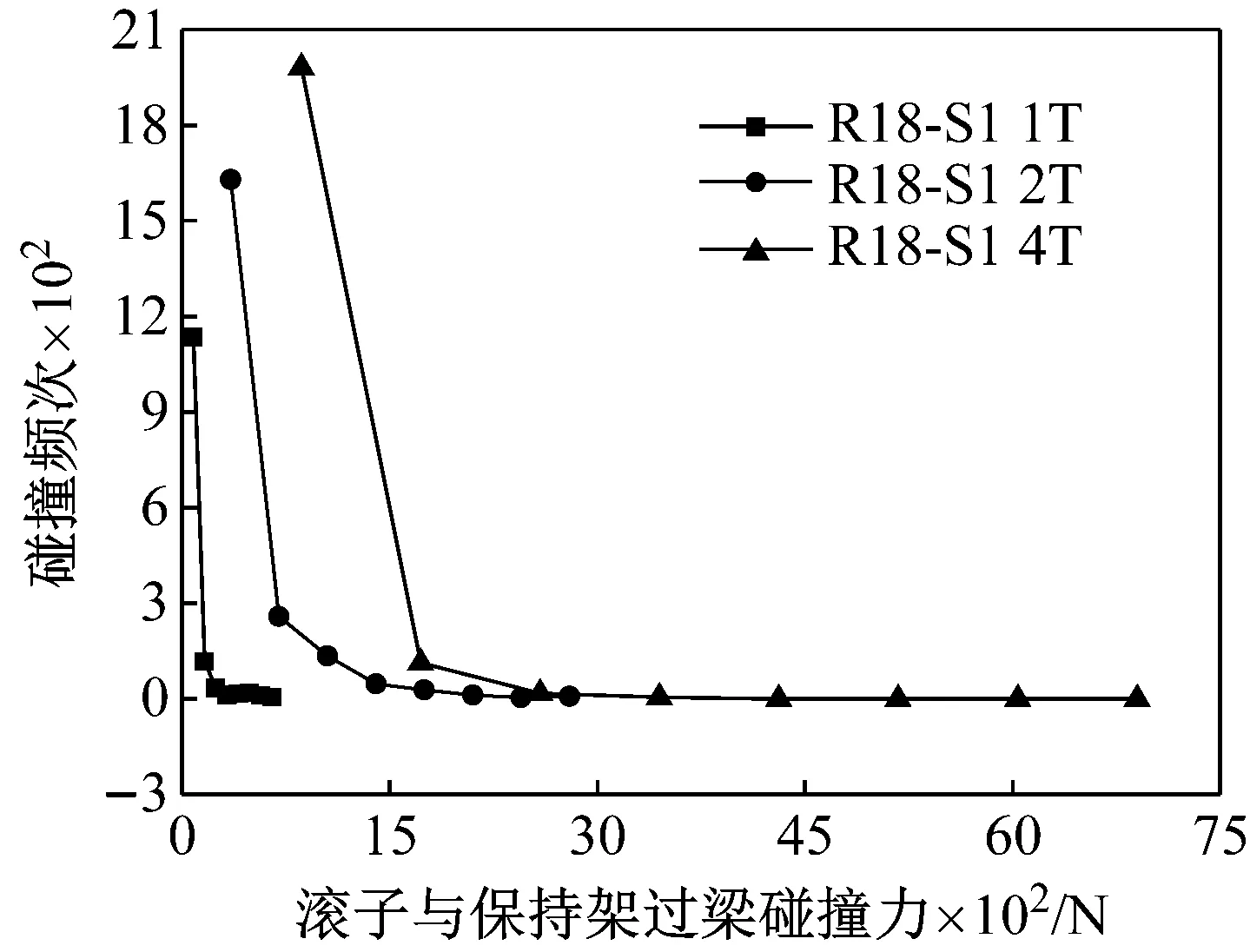
图15 不同冲击作用时间下滚子与过梁碰撞力的频数统计

Fig.15 Cage bridge and roller contact force frequency statistics under different impact time

2.6 疲劳强度

本文模仿单个车轮扁疤冲击对轴箱轴承保持架进行仿真分析，而实际铁路车轮扁疤不止一个，车轮长期运转车轮外圆会出现多边形，滚子对保持架过梁的冲击频率要远高于此。

3 保持架强度分析

3.1 冲击强度

由上文分析可知当轮轨之间产生较大的碰撞冲击时，在垂向方向上轮对会获得较大的初始速度。从能量守恒的角度上分析，这个较大的初始动能一部分会转化成一系悬挂的弹性势能和阻尼器消耗，另外较大一部分是被跟轮轴直接刚性连接的轴箱轴承所吸收，是造成保持架过梁直接断裂的根源所在。

根据塑料冲击强度测试标准[21]，对塑料保持架可以采用简支梁冲击试验的方法测定保持架冲击强度[22]。无缺口试样简支梁冲击强度(单位：kJ/m2)定义为

(21)

式中:Ec为试样吸收的冲击能量，J；h为试样截面厚度，mm；b为试样截面宽度，mm；

试验采用的是摆锤上升一定的高度自由下落，将其重力势能转化成冲击动能将试样冲断。实际轴承服役过程中保持架过梁主要承受滚子的随机碰撞作用力，这种受力状态跟简支梁冲击试验近似。由前文分析当有外部冲击时，这种碰撞力会显著增大，滚子相对保持架过梁的冲击动能会导致过梁断裂。滚子相对过梁的冲击动能为

(22)

式中:mr为滚子的质量，kg；ΔV为滚子相对于过梁的速度，m/s。

由上述两式，Er=Ec可得

(23)

经查阅GRPA66-25无缺口冲击强度为65 kJ/m2,本文计算采用轴承滚子质量为0.384 kg，保持架过梁截面面积为98.6 mm2，可以近似求得冲击强度对应的相对速度ΔV为5.78 m/s。那么如果滚子和保持架之间碰撞相对速度高于该值保持架过梁发生直接断裂的几率会大大增加。

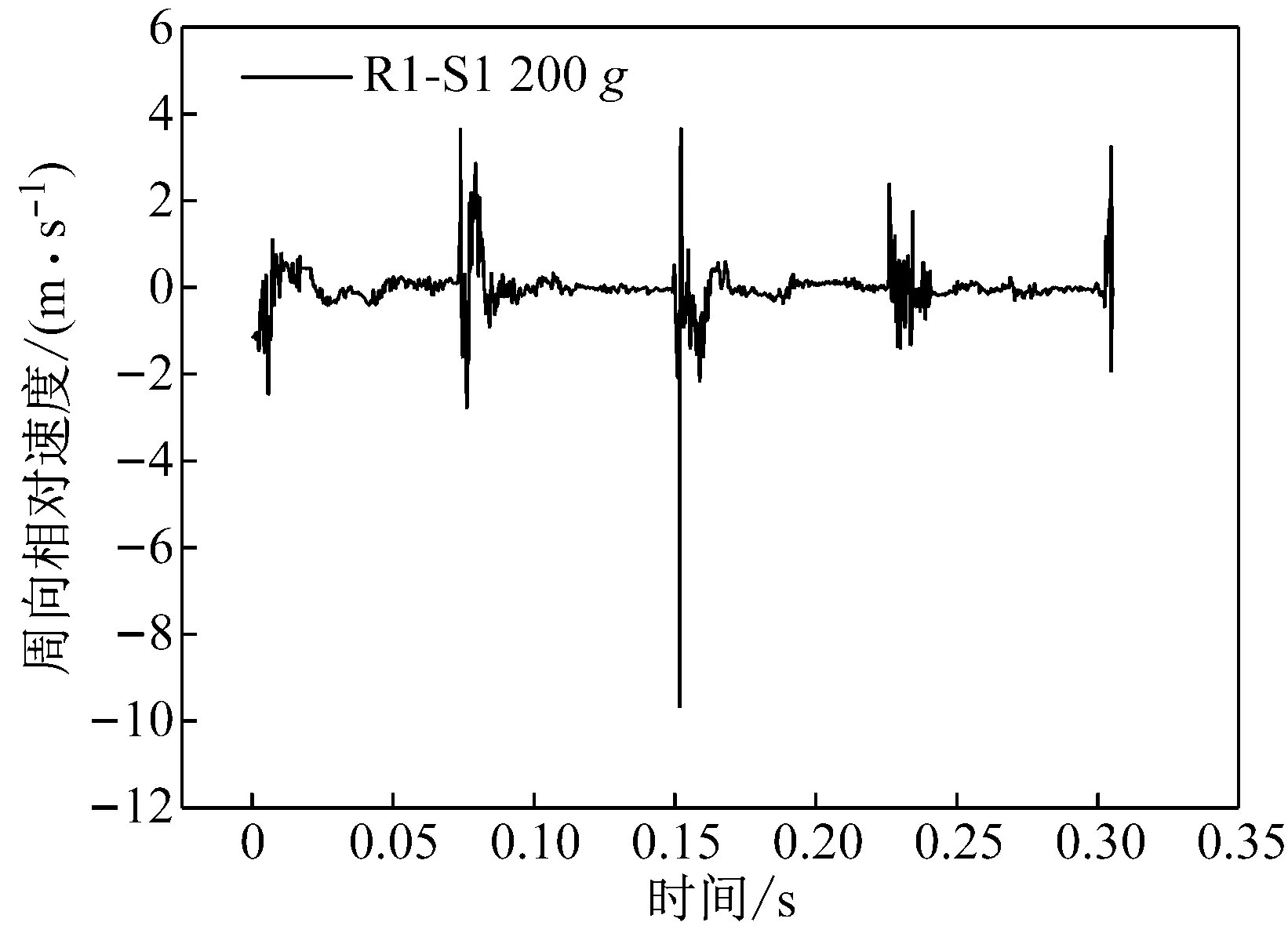
图16 冲击加速度为200g时滚子和过梁的相对速度

Fig.16 Relative velocity between cage bridge and roller when impact acceleration is 200g

对仿真计算结果进行分析，提取出1号滚子(R1)和1号过梁(S1)沿圆周方向的运动速度差如图所示，当冲击加速度逐渐增大时，如图17两者之间速度差基本上呈线性增加，对数据进行拟合，得到滚子与过梁之间周向速度差与冲击加速度之间的关系式：ΔV=0.048a-1.045，将最大周向速度差5.78 m/s代入可得冲击加速度为140g时可能超过保持架的冲击强度。

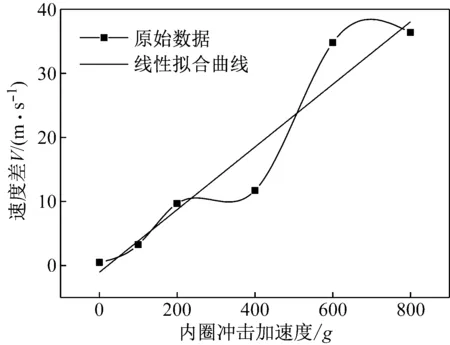
图17 滚子与过梁之间相对速度随冲击加速度的变化

Fig.17 Relative velocity between cage bridge and roller varies with impact acceleration

3.2 弯曲强度

根据上述分析结果本文进行进一步的有限元分析计算，采用ABAQUS的瞬态动力学分析方法分析滚子与保持架过梁碰撞瞬间应力分布，如图18所示，滚子设置为刚体以5.78 m/s的初速度撞击保持架过梁，从结果可以看出碰撞时间大约8×10-4s，产生最大应力出现在过梁侧梁过渡处，约为209 MPa。略小于保持架材料的弯曲强度228 MPa。

图18 滚子与过梁之间碰撞有限元瞬态动力学分析

Fig.18 FEA transient dynamic analysis of collision between cage bridge and roller

对滚子不同的初始速度进行计算，结果如图19所示，随滚子相对于过梁的初始速度的增加，最大应力线性增加，最大应力点均处于过梁与侧梁过渡处。根据拟合可求得最大应力与相对初始速度的关系式：Mmax=26.88ΔV+49.68，弯曲强度对应的速度值为6.63 m/s，由3.1分析可得对应的加速度值约为158g。

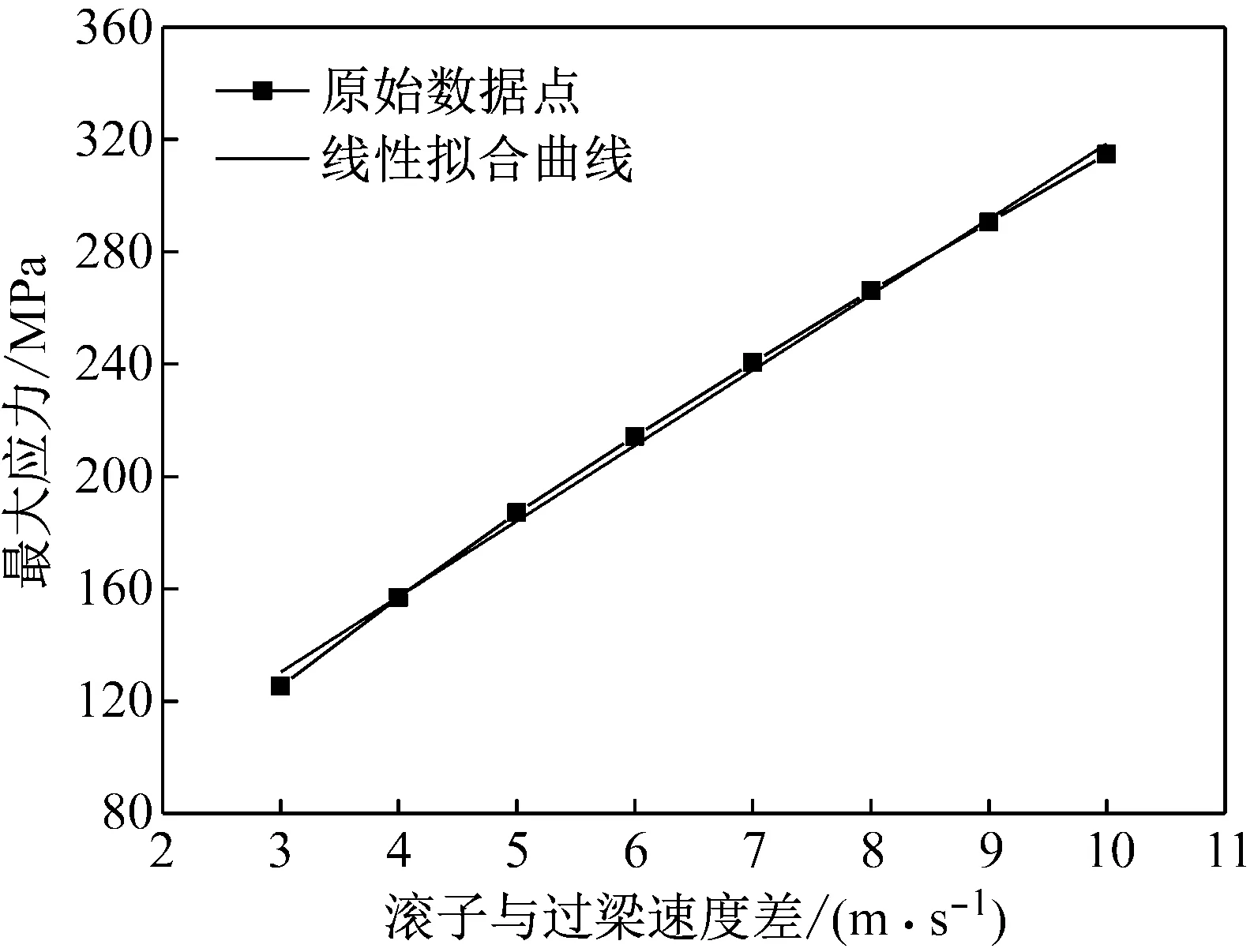
图19 保持架受最大应力随滚子相对保持架初始速度变化

Fig.19 Cage maximum stress varies with relative velocity between cage bridge and roller

综合塑料保持架的冲击强度和弯曲强度，该轴箱轴承实际工作中轮轴冲击加速度若高于158g就会造成保持架过梁的直接断裂。

由于仿真分析跟实际保持架受力边界条件有一定的区别，针对具体的保持架结构还需要用试验去验证保持架断裂时轮轴的冲击加速度。

4 结 论

(1) 当无冲击发生时，对于仅承受径向力的轴承在稳定转速下，当保持架由外圈引导时，滚子与保持架碰撞规律在轴向平面的圆周方向达到一个动态平衡：在承载区的滚子与保持架过梁几乎无碰撞，在非承载区滚子阻碍保持架的转动，出承载区时两者碰撞波动较显著。

(2) 轮轨冲击发生时，产生较大的轮轴垂向冲击加速度会带来保持架的运行不稳定性及滚子与保持架之间的剧烈碰撞，碰撞作用力随着冲击加速度的增加显著增加，碰撞频次也剧烈增加，会加速保持架的疲劳断裂。

(3) 经过保持架强度分析可知对于本文讨论轴箱轴承当轮轨冲击加速度足够高(超过158g)时，滚子相对于保持架的冲击动能会导致保持架过梁的直接断裂。

(4) 扁疤尺寸的增大和车速的增加都会放大轴承受到的冲击作用加速度，随着列车的不断提速要更加重视轮轨冲击给轴箱轴承带来的伤害，一方面应积极消除车轮扁疤及其他轮轨冲击因素的影响，另一方面要对保持架进行结构优化设计提高其结构强度。

致谢

感谢辽宁重大装备制造协同创新中心支持。

[1] 何强，李安玲，张继祝，等. 高速列车轴承的发展趋势[J]. 徐州工程学院学报(自然科学报)，2012, 27(1): 58-64.

HE Qiang, LI Anling, ZHANG Jizhu, et al. The development trend of high-speed railway bearing[J]. Journal of Xuzhou Institute of Technology(Natural Science), 2012, 27(1): 58-64.

[2] DYBA G J, KLECKER R J. High speed cylindrical roller bearing analysis//SKF computer program “CYBEAN”[R]. NASA-CR-159460, 1978.

[3] GUPTA P K. Modeling of instabilities induced by cage clearance in cylindrical roller bearings[J]. Tribology Transactions, 1991, 34(1): 1-8.

[4] 周延泽，陆震，沈心敏. 高速球轴承保持架疲劳断裂原因分析[J]. 机械设计与制造，2001(1): 1-3.

ZHOU Yanze, LU Zhen, SHEN Xinmin. The causes of fatigue fracture of cage in high speed ball bearing[J]. Machinery Design & Manufacture, 2001(1): 1-3.

[5] YOSHIDA T, TOZAKI Y, MIYAKE H, et al. Analysis of cage slip in cylindrical roller bearings considering non-Newtonian behavior and temperature rise of lubricating oil[J]. Journal of Japanese Society of Tribologists, 2008, 53(11):752-761.

[6] 李晌，蒋新力，姜艳红，等. 高速圆柱滚子轴承柔性保持架的动力学分析[J]. 轴承，2010(7): 1-5.

LI Shang, JIANG Xinli, JIANG Yanhong, et al. Dynamic analysis on flexible cage in high speed cylindrical roller bearing[J]. Bearing, 2010(7): 1-5.

[7] 邓四二，顾金芳，崔永存，等. 高速圆柱滚子保持架动力学特性[J]. 航空动力学报，2014, 29(1): 207-215.

DENG Si’er, GU Jinfang, CUI Yongcun, et al. Analysis on dynamic characteristics of cage in high-speed cylindrical roller bearing[J]. Journal of Aerospace Power, 2014, 29(1): 207-215.

[8] YE Z H, WANG L Q. Effects of axial misalignment of rings on the dynamic characteristics of cylindrical roller bearings[J]. Proceedings of the Institution of Mechanical Engineers Part J Journal of Engineering Tribology, 2016, 230(5): 525-540.

[9] 姚廷强，黄亚宇，王立华. 圆柱滚子轴承多体接触动力学研究[J]. 振动与冲击， 2015, 34(7): 15-23.

YAO Tingqiang, HUANG Yayu, WANG Lihua. Multibody contact dynamics for cylindrical roller bearing[J]. Journal of Vibration and Shock, 2015, 34(7): 15-23.

[10] XU Lixin. A general method for impact dynamic analysis of a planar multi-body system with a rolling ball bearing joint[J].Nonlinear Dynamics, 2014, 78(2): 857-879.

[11] EVANS R D, HOUPERT L, SCANDELLA F, et al. Dynamic analysis of rail gearbox bearings[J]. Proceedings of the Institution of Mechanical Engineers, Part F： Journal of Rail & Rapid Transit, 2016,231(8):991-996.

[12] LONSDALE C, RUSIN T, HAY T, et al. Research to understand the effects of wheel impact loads on wheel stress levels[C]// Joint Rail Conference. Los Angeles,2009: 99-105.

[13] 俞良家. 轮轨冲击分析[J]. 铁道标准设计，1985(3): 21-24.

YU Liangjia. Analysis of wheel/rail impact[J]. Railway Standard Design, 1985(3): 21-24.

[14] 王艺佳，曾京，高浩，等. 车轮扁疤引起的轮轨冲击分析[J].西南交通大学学报，2014, 49(4): 700-705.

WANG Yijia, ZENG Jing, GAO Hao, et al. Analysis of Wheel/Rail Impact Induced by Wheel Flats[J]. Journal of Southwest Jiaotong University, 2014, 49(4): 700-705.

[15] WEINZAPFEL N, SADEGHI F. A discrete element approach for modeling cage flexibility in ball bearing dynamics simulations[J]. Journal of Tribology, 2009，131(2): 21102-21112.

[16] HUNT K H, CROSSLEY F R E. Coefficient of restitution interpreted as damping in vibroimpact[J]. Journal of Applied Mechanics, Transactions of the ASME, 1975, 42(2): 440-445.

[17] HARRIS T A. Rolling bearing analysis[M]. New York: John Wiley & Sons Inc, 2006.

[18] SAKAGUCHI T, HARADA K. Dynamic analysis of cage behavior in a tapered roller bearing[J]. Journal of Tribology, 2006, 128(3):165-166.

[19] 刘秀海. 高速滚动轴承动力学分析模型与保持架动态性能研究[D]. 大连:大连理工大学，2011.

[20] 魏胜民. 高速铁路钢轨短波不平顺检测研究[J]. 中国铁路，2011(6): 16-18.

WEI Shengmin. Research of high-speed rail shortwave irregularity detection[J]. Chinese Railways, 2011(6): 16-18.

[21] Plastics-determination of charpy impact properties: ISO 179-1—2010[S].

[22] 赵文聘. 轴承保持架用PA66玻纤增强料的研究[J]. 塑料工业，2002，30(1): 13-15.

ZHAO Wenpin. Study of glass fiber reinforced PA66 used for bearing maintenance shelving[J]. China Plastics Industry, 2002,30(1): 13-15.