基于平稳非高斯结构响应前四阶矩的首次穿越概率计算

张龙文， 卢朝辉,2， 赵衍刚,2

(1.中南大学 土木工程学院，长沙 410075； 2.中南大学 高速铁路建造技术国家工程实验室，长沙 410075)

在工程应用中，首次穿越概率用以描述结构在动力荷载作用下的动力可靠性问题。对此类问题，结构失效以其动力反应(如控制点的应力，或控制点、控制层的位移、速度、加速度等)首次穿越临界值水平为标志[1]。临界界限可以是屈服或极限应力、应变或位移。国内外众多学者对此问题进行了大量的研究[2-7]，但是到目前为止，首次穿越问题甚至是最简单的单自由度线性振子在高斯白噪声激励下的首次穿越概率都没有精确的解析解[8-11]。在大多数情况下，假设结构响应是高斯的，以及结构响应的穿越服从Poisson分布。

当线性结构的激励被定义为高斯过程模型时，结构的响应也是高斯的。在这种情况下，从概率与统计的角度来讲，结构的响应可被均值和标准差完全定义。然而，当结构行为是非线性，或者激励是非高斯过程，亦或两者兼而有之，结构的响应将不是高斯过程，因此利用高斯模型计算首次穿越概率是不准确的。此时，对于非高斯过程的描述，需要用到更高阶的统计矩。

非高斯过程的描述，可以通过一系列的分布方法[12-13]找到简单的转换函数进行非高斯过程与标准高斯过程之间的转换。基于转换的思路，许多学者提出了多种非线性模型用以描述非高斯过程。例如，基于结构反应矩(偏态系数和峰度系数等)，利用Gram-Charlier和Edeworth级数可以得到反应的全概率分布，进而变换为标准高斯过程[14]。但Gram-Charlier和Edeworth级数可能产生多个模型甚至负的概率密度函数和超越率。Winterstein提出了基于Hermite 矩模型的Winterstein (1988)多项式，利用结构响应的前四阶矩将非高斯结构响应变换为标准高斯过程[15]。基于Wintertein(1988)的多项式，He等[16]考虑了穿越的群超效应和初始条件计算了平稳非高斯结构响应的首次穿越概率。然而，基于Winterstein (1988)多项式计算结果与Monte-Carlo模拟计算结果差别显著，尤其是硬化反应情况中。该计算结果产生差异的原因在于转换精度不足。另外，在一些相关文献中[17-19]也发现，Winterstein (1988)多项式在软化和硬化的非高斯过程中并不精确。因此，对于非高斯结构响应的首次穿越概率的计算，提高转化模型的精度是必要的。

本文针对Winterstein (1988)多项式转换的不足，采用精度更能满足要求的Winterstein修正模型Winterstein(1994)[20]，以及Ding和Chen模型[21]，再利用考虑群超效应和初始条件的Poisson过程模型[22]，建立软化和硬化非高斯结构响应的首次穿越概率解析表达式。以线性与非线性单自由度振动系统为例，对本文修正的方法、已有方法以及Monte Carlo模拟计算结果进行比较分析，验证该方法在首次穿越概率计算中的有效性与准确性。

1 平稳非高斯随机过程的首次穿越概率

在结构安全分析中，首次穿越概率Pf(T), 按照超越数服从泊松分布的假定表示为

Pf(T)=1-exp[-E[N+(T)]]

(1)

式中:E[N+(T)]是在时间段[0,T]内X(t)穿过界限的超越数。对于工程中感兴趣的平稳情况，有E[N+(T)]=v+T,其中v+代表由Rice公式计算的平均超越率。它可以表示为

(2a)

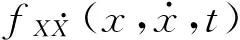
(2b)

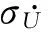
(2c)

式中:ω0是振动系统的无阻尼固有频率。

如果结构响应是窄带反应过程或者超越界限较低，此时穿越倾向于成群发生，需要对平均超越率进行修正[22-23]。当同时考虑平稳开始的初始条件及群超尺度〈cs〉时，式(1)可以被进一步改进为[24]

(3a)

其中

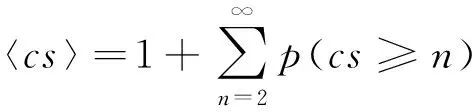
(3b)

(3c)

(3d)

Pf(0)=1-Φ[u(x)]

(3e)

式中:Pf(0)是T=0时的瞬时失效概率；RU(τ)是标准高斯过程U(t)的自相关函数，可以表示为

(3f)

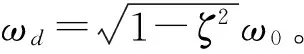
2 基于修正模型的首次穿越概率计算

由于Winterstein(1988)多项式转化精度的不足，本节首先介绍了Winterstein(1994)软化模型以及Ding和Chen硬化模型，并给出了相应的等效高斯分位数。接着，对两种模型的精度进行分析，讨论了模型的精度。最后，说明了两种模型在软化与硬化非高斯结构响应的首次穿越概率计算过程。

2.1 Winterstein(1994)多项式及其等效高斯分位数

Winterstein等[25]提出了修正的Winterstein(1994)多项式

(4a)

式中:μX和σX分别为随机过程X(t)的均值和标准差；U(t)是标准高斯过程；c3、c4以及κ为多项式系数，可通过偏态系数和峰度系数计算得到

(4b)

(4c)

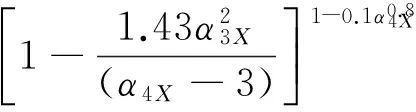
(4d)

(4e)

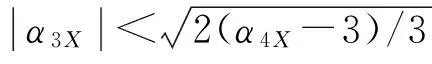
对于修正的Winterstein(1994)多项式的等效高斯分位数可以表示为

(5a)

(5b)

2.2 改进的硬化模型及其等效高斯分位数

Ding等基于正交展开的方法提出了一个更为匹配的硬化模型(α4X<3)。该硬化模型可以表示为

X(t)=μX+σXg(U)

(6a)

式中

(6b)

j=b3/(3b4),k=(b2-b3α3X-b4α4X)/(3b4)

(6c)

式中:b2，b3，b4为模型系数，表示为

φ=[1-0.06(3-α4X)]1/3

(6d)

该模型的等效高斯分位数为

(7a)

式中，

放疗的毒性反应较强，治疗期间应采取以下护理措施：①照射野皮肤护理。照射野皮肤会产生发痒、红斑、脱皮等症状，或发生放射性皮炎，不宜抓挠，避免冷热刺激，不宜反复清洗，放射性皮炎患者可在患处涂抹冰片滑石粉；②骨髓抑制的处理。长时间大面积放疗，会引起骨髓造血功能损伤，白细胞下降，病情严重时，应停止放疗，应用升白细胞药物，同时做好保护性隔离措施；③食道反应的护理。患者存在吞咽困难的问题，治疗期间宜进流质/半流质食物，忌食粘性或带骨头、鱼刺的食物，吞咽疼痛患者，可在餐前10 min口服适量黏膜表面麻醉剂，以缓解疼痛。

m1=-b4α3X,m2=b2-b3α3X-b4α4X+3b4,

(7b)

它的适用范围为(1.35α3X)2+1.25≤α4X<3。因此，该模型适用于硬化非高斯过程。

2.3 模型精度分析

2.3.1 Winterstein(1994)多项式精度调查

由于Winterstein(1994)以及Winterstein(1988)的软化模型为一元三次多项式，在此根据Fleishman[27]的矩匹配方法，计算多项式系数的准确值，用以说明Winterstein(1994)以及Winterstein(1988)的软化模型的精度问题。对于一般的一元三次多项式可以表达为

(8)

在X(t)的前四阶矩已知的情况下，基于矩匹配方法，多项式系数a1,a2,a3,和a4与前四阶矩的关系，可以表达为[28]

a1+a3=0

(9a)

(9b)

(9c)

(9d)

简化等式(9a)～(9d)，可以根据等式(10a)～(10f)计算a2与a4，表达如下

(10a)

3A1A3+3A4=α4X

(10b)

式中，

(10c)

(10d)

(10e)

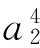
(10f)

当a2与a4计算后，a1与a3可以通过下式计算，

(11)

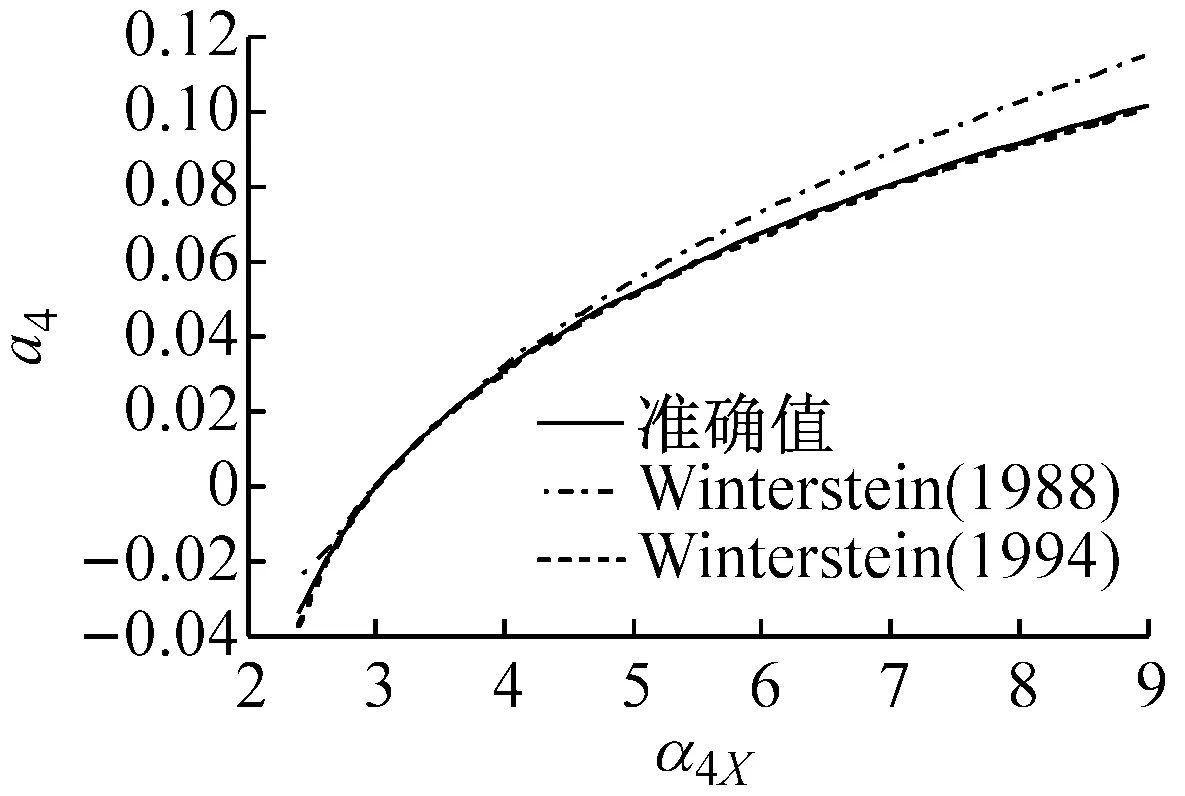
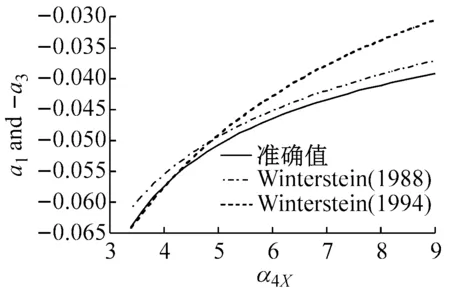
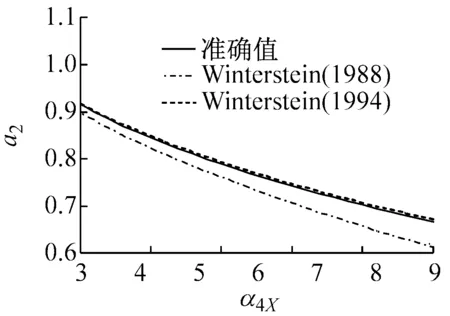
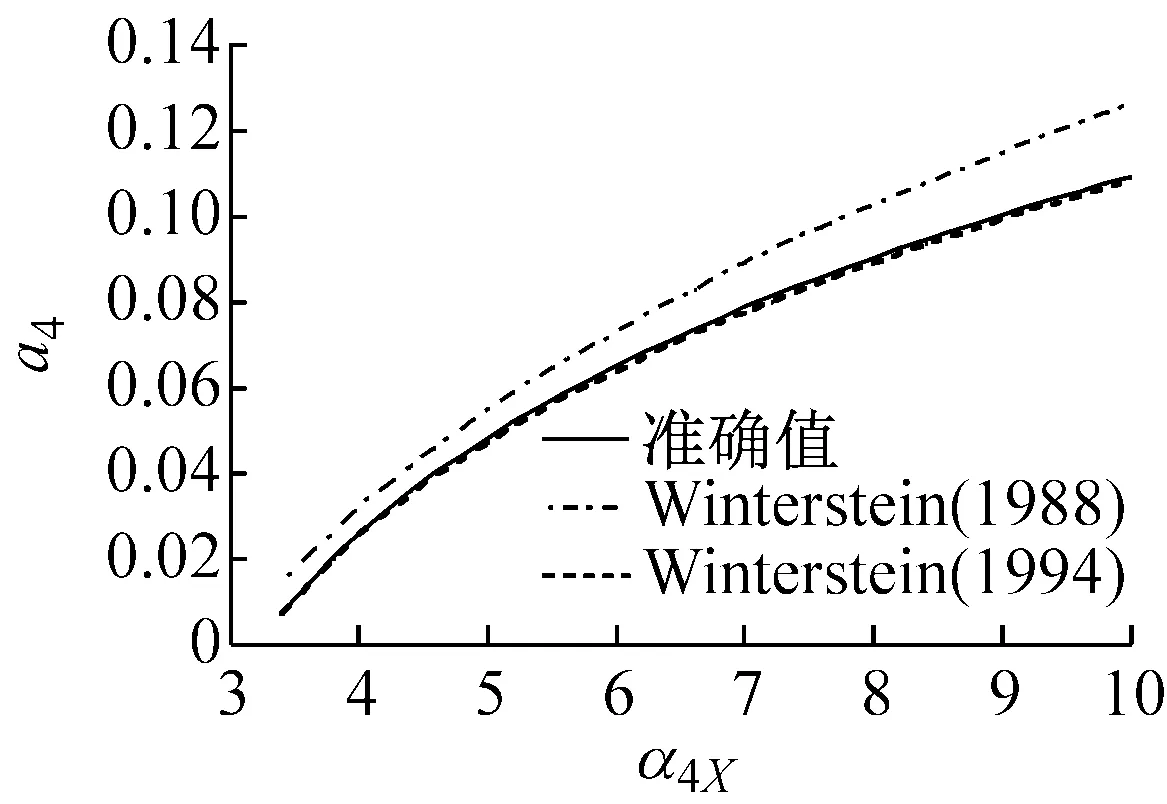
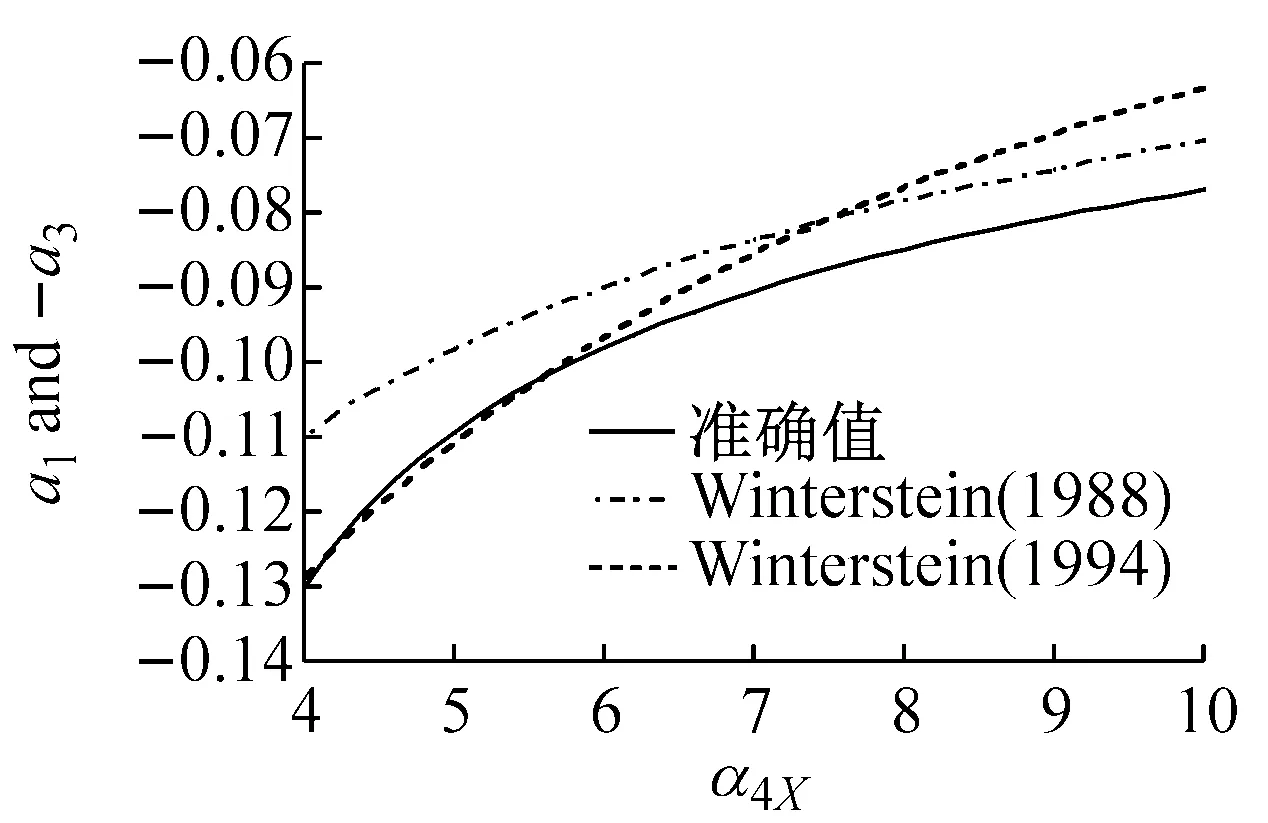
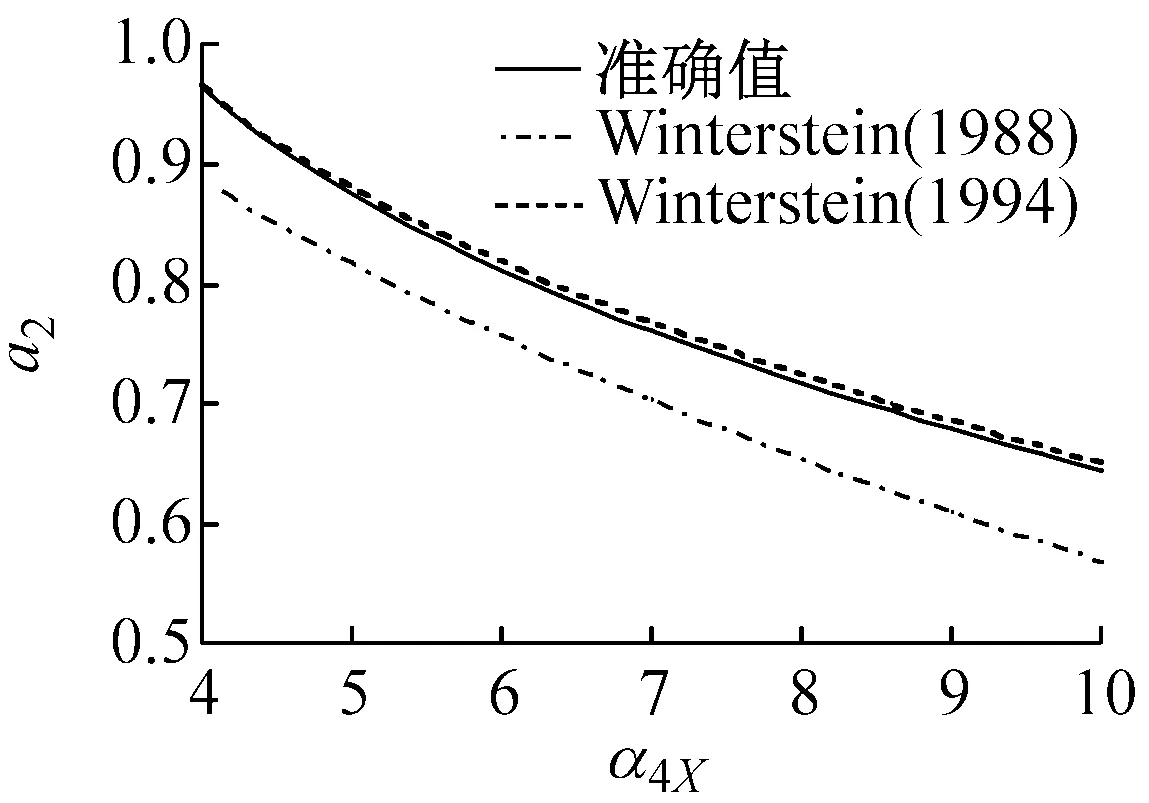
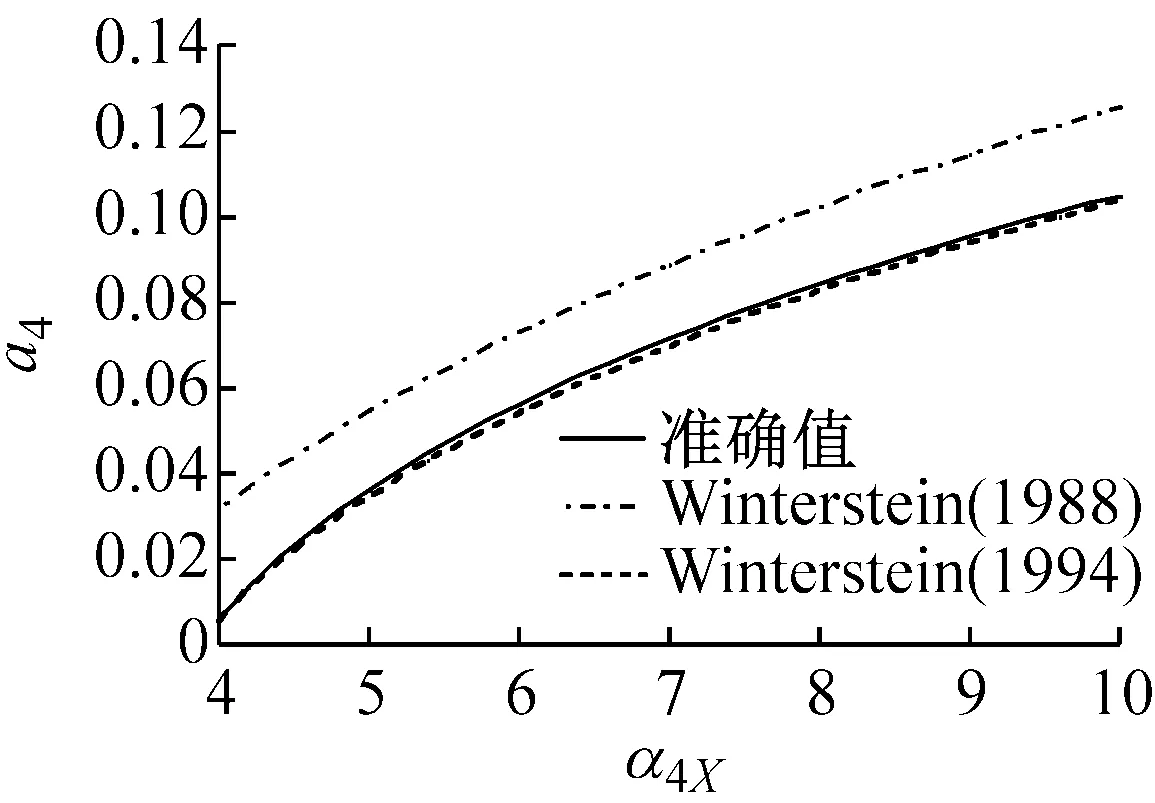
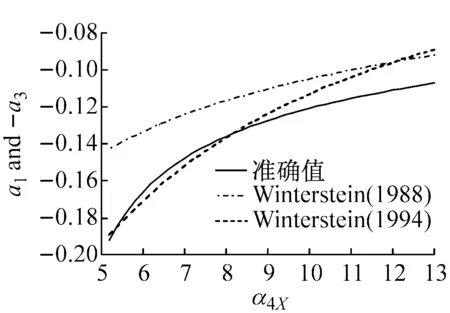
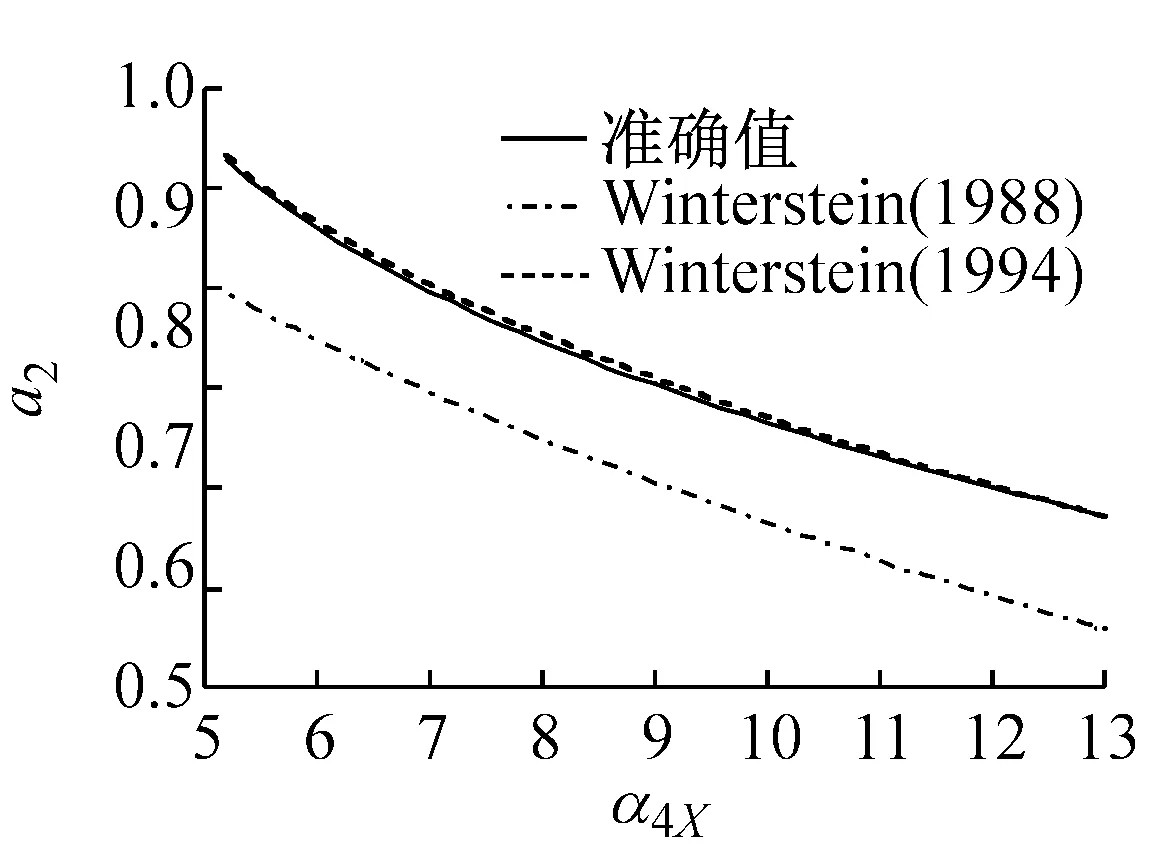
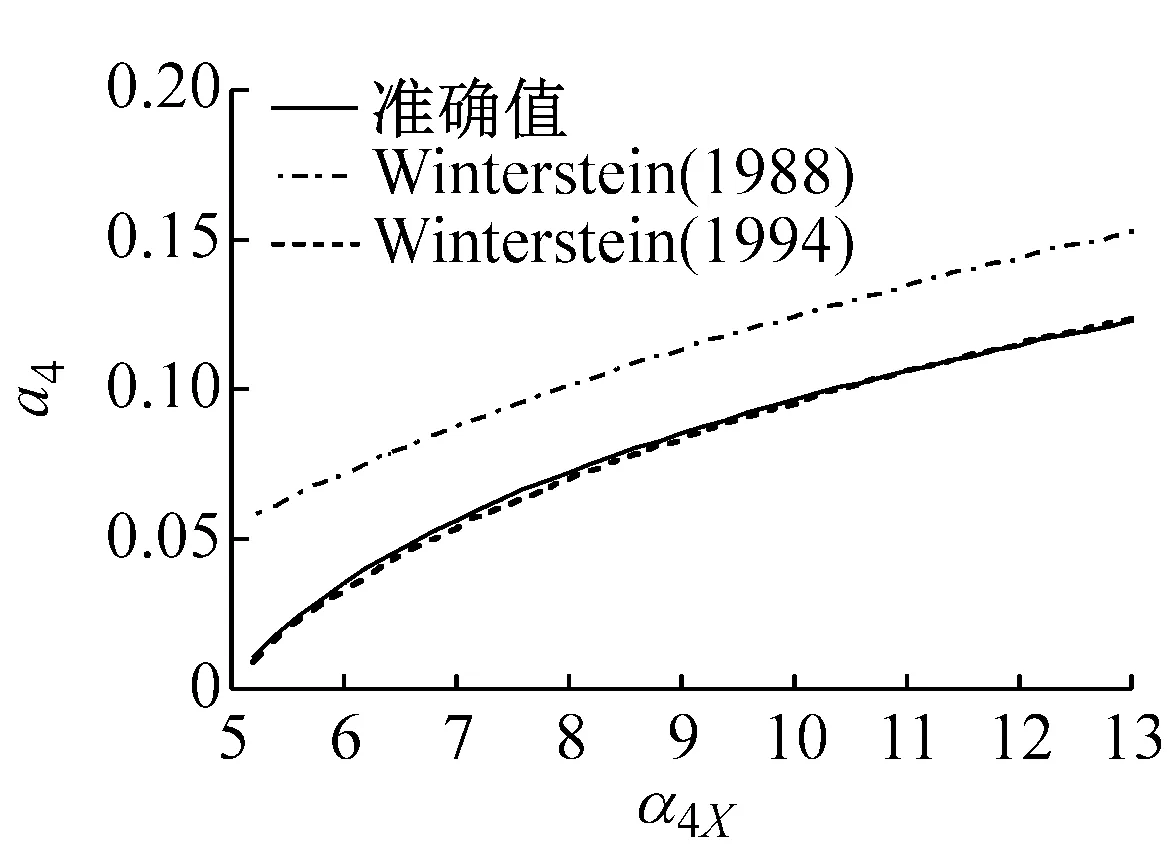
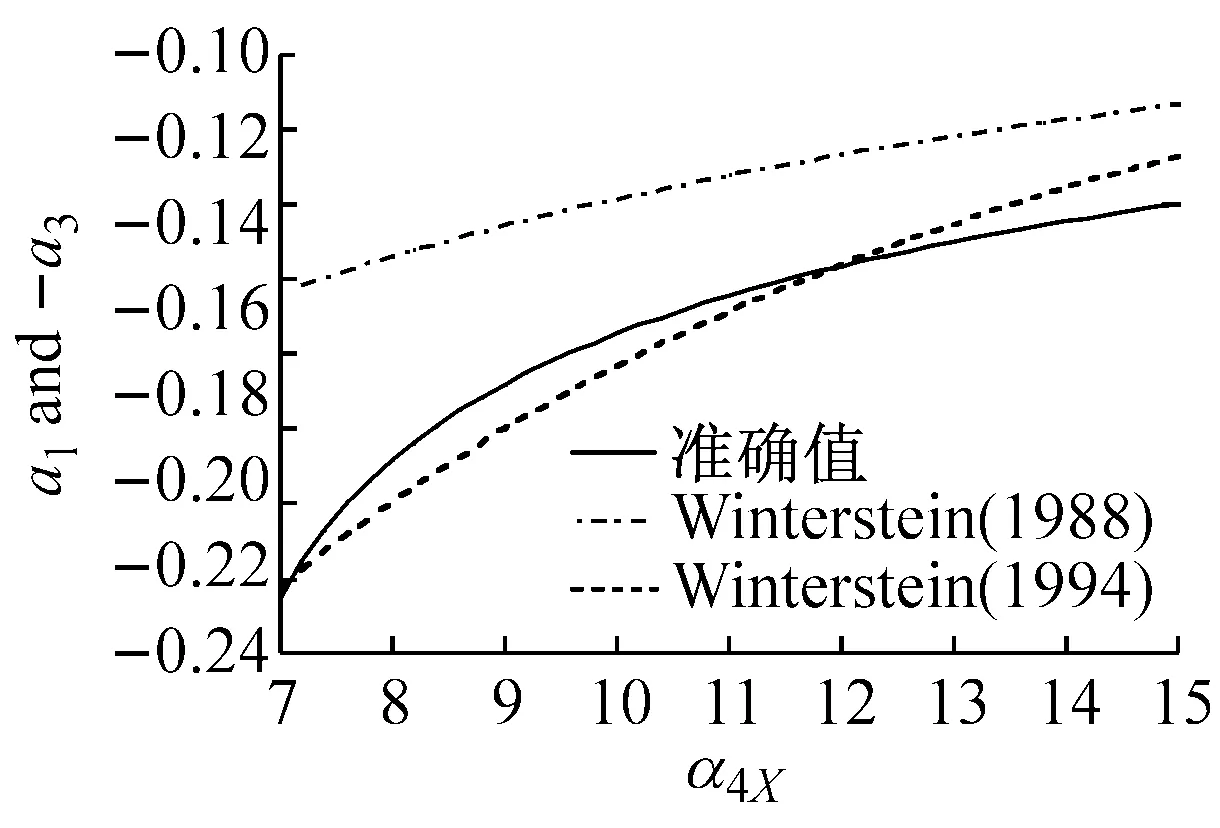
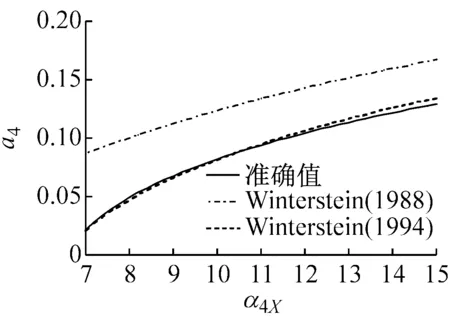
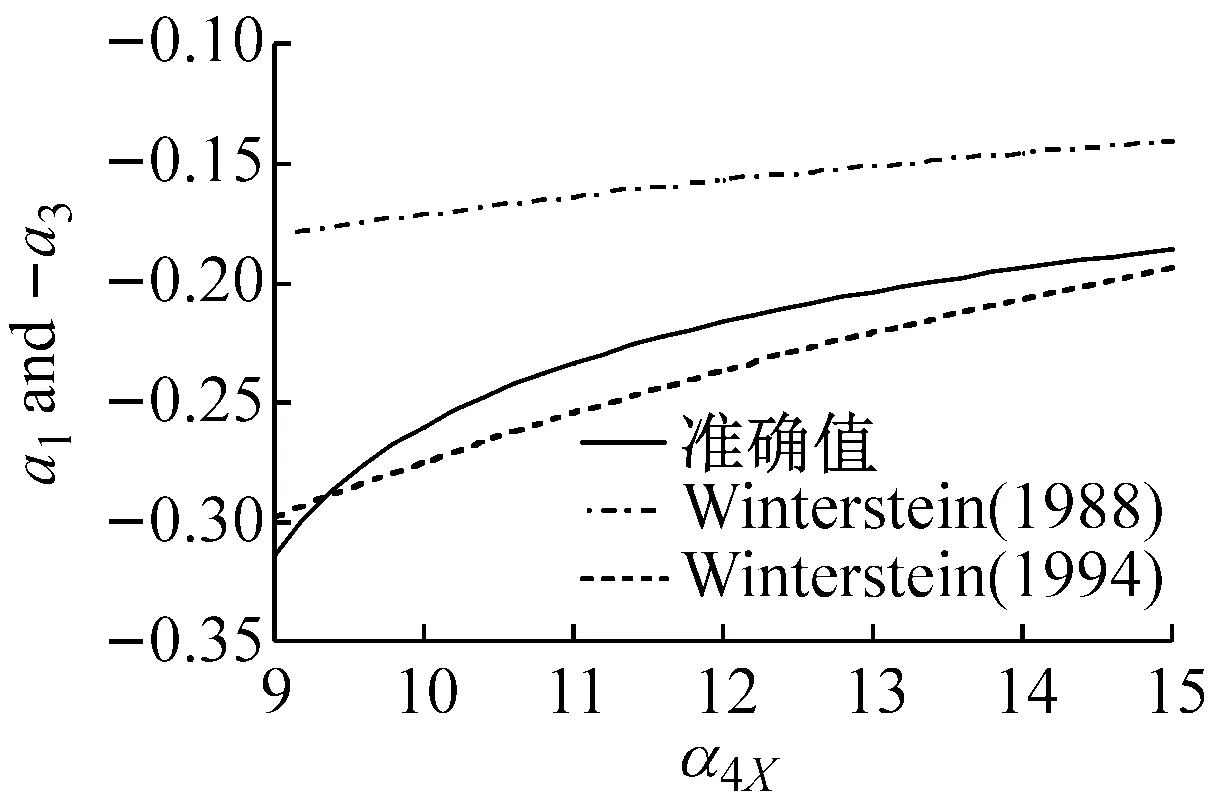
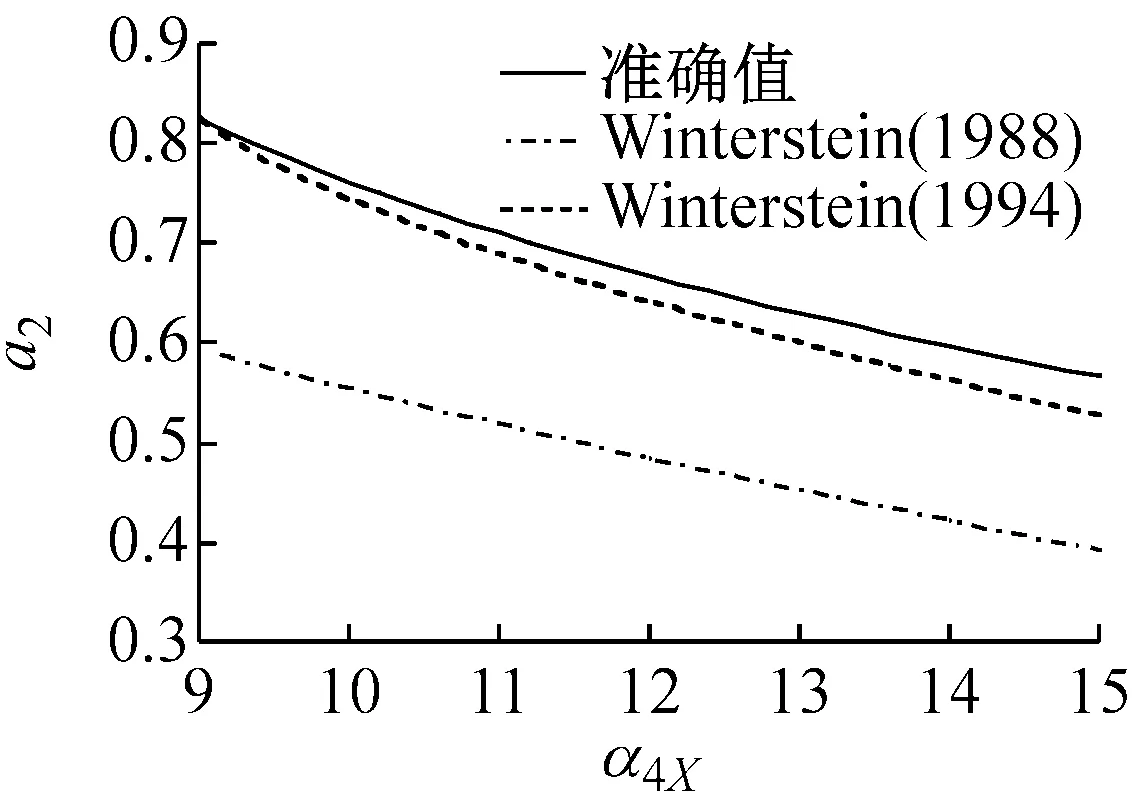
图1表示在不同偏态系数α3X下，随着峰度系数α4X变化的Winterstein(1988)与Winterstein(1994)多项式系数以及准确值。从图中的计算结果表明：

(1) Winterstein(1988)模型计算的各系数与准确值的差异大，且随着偏态系数α3X的增大而变大。

(2) Winterstein(1994)模型计算的各系数改进了Winterstein(1988)模型的不足，能够与准确值吻合，特别是a2与a4系数与准确值基本重合。另外，从图1(f)中可以看出，当偏态系数α3X=2.0时，随着峰度系数α4X的增大，Winterstein(1994)模型各系数的精度开始下降。因此，虽然Winterstein(1994)模型优于Winterstein(1988)模型，但更适用于α3X<2.0的情况。从等式(4b)～(4e)可以看出α3X的正负值只改变c3的正负号,因此，当α3X取负值时，同样可以得到图1的类似结果。

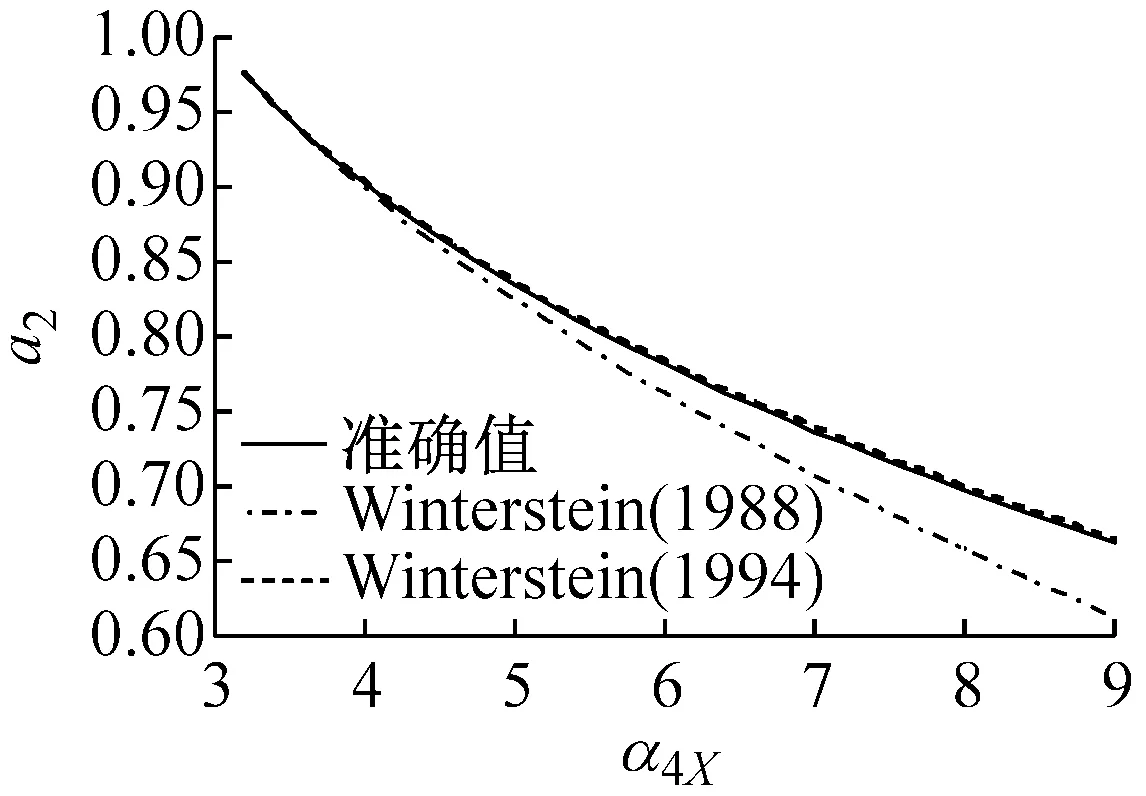
(a) α3X=0

(b) α3X=0.4

(c) α3X=0.8

(d) α3X=1.2

(e) α3X=1.6

2.3.2 Ding和Chen模型精度调查

对于等式(6a)所示Ding和Chen模型的逆函数形式可以表达为

(12)

对等式(12)取期望，可得，

(13)

该修正的硬化模型保证了标准高斯过程U(t)均值恒为0，改进了Winterstein(1988)模型中U(t)均值不为0的缺陷。另外，该模型的模型系数在文献[21]中通过最小二乘法拟合得到，验证了模型的精度满足要求。为了进一步分析Ding和Chen模型的精度，通过计算该模型的偏态系数与峰度系数，并与它们的目标值(α3X,α4X)进行比较分析。该模型的前四阶中心矩可以通过下式计算

(14a)

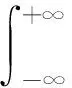
(14b)

式中φ(·)为标准正态分布的概率密度函数，表达为

(15)

则该模型计算的偏态系数γ3与峰度系数γ4可以表达为

(16)

为了便于分析Ding和Chen模型计算的偏态系数γ3与峰度系数γ4与目标值的误差，将偏态系数与峰度系数的误差值分别记为δα3X与δα4X。它们可以表达为

δα3X=γ3-α3X,δα4X=γ4-α4X

(17)

通过以上方法，计算得到偏态系数与峰度系数的误差如图2与图3所示。图2，图3分别为偏态系数与峰度系数误差结果。从图中计算结果表明：

(1) 从图2可以看出，Ding和Chen硬化模型偏度系数计算值与目标值误差基本控制在-0.1与0.1之间。当峰度系数α4X=1.5～2时，离散性较大。当峰度系数α4X=2～3时离散性变小，且误差趋近于0。

(2) 从图3可以看出，Ding和Chen硬化模型峰度系数计算值与目标值误差控制在-0.05与0.05之间。当偏态系数α3X=0时，模型峰度系数计算值与目标值的误差最小。

2.4 基于修正方法的首次穿越概率

根据Winterstein(1994)以及Ding和Chen模型，基于改进方法计算平稳非高斯结构响应的首次穿越概率的步骤如下：

(1) 计算平稳非高斯过程的前四阶矩。

(2) 确定转换模型及其系数；如果峰度系数α4X>3，选用Winterstein(1994)模型，再根据式(4b)和(4e)计算转换模型系数；如果峰度系数α4X<3，选用Ding和Chen模型，根据式(6b)～(6d)计算转换模型系数。

(3) 如果峰度系数α4X>3，根据式(5a)～(5b)计算等效高斯分位数；如果峰度系数α4X<3，根据式(7a)～(7b)计算等效高斯分位数；确定结构响应的超越界限或超越水平x，将平稳非高斯结构响应映射为标准高斯过程。

(4) 最后，根据基于平稳高斯结构响应的Poisson模型即式(3a)～(3f)计算平稳非高斯结构响应的首次穿越概率。

如图2和3所示。

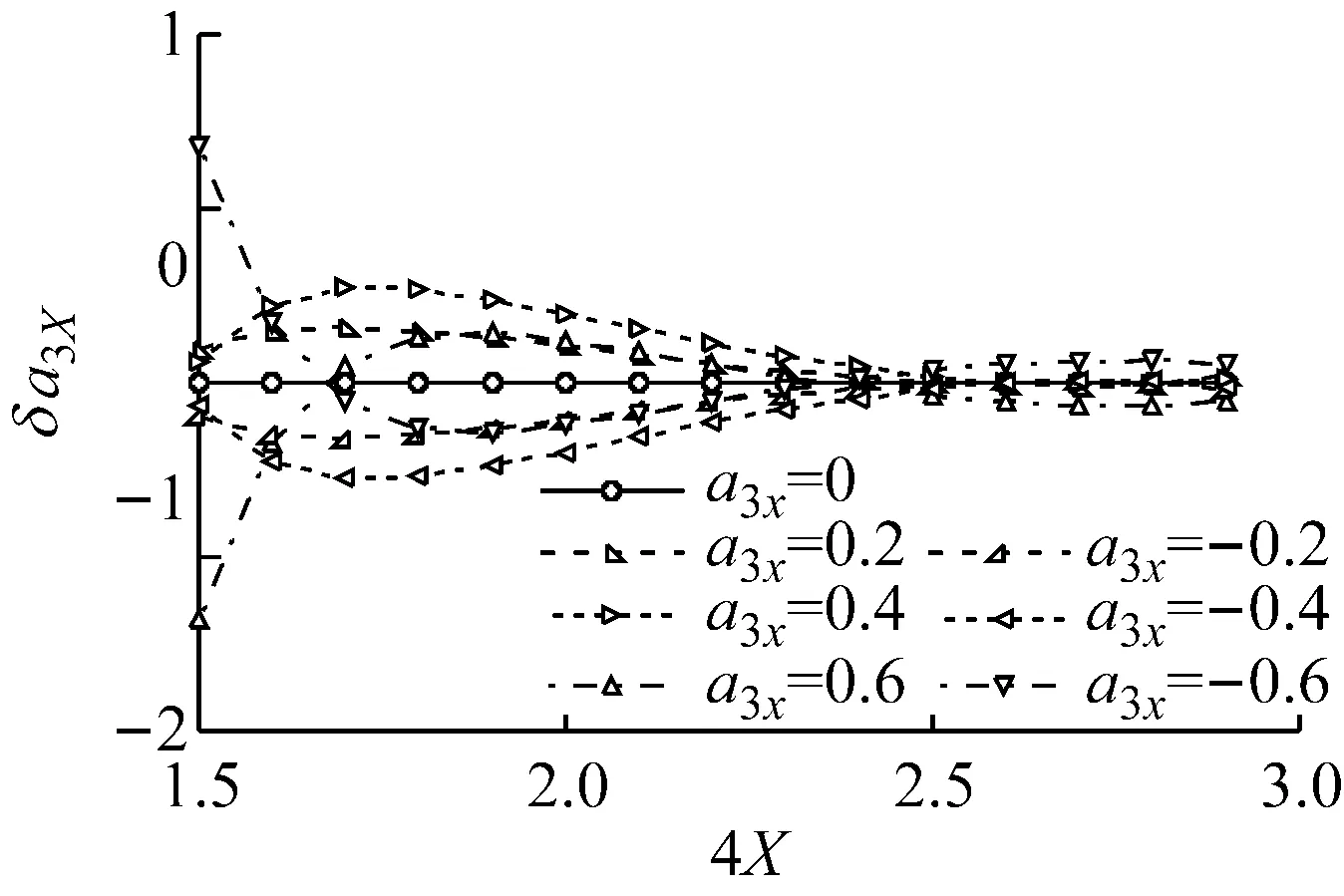
图2 Ding和Chen硬化模型偏态系数计算值与目标值误差

Fig.2 bias between the estimations based on Ding and Chen model and the target values for skewness

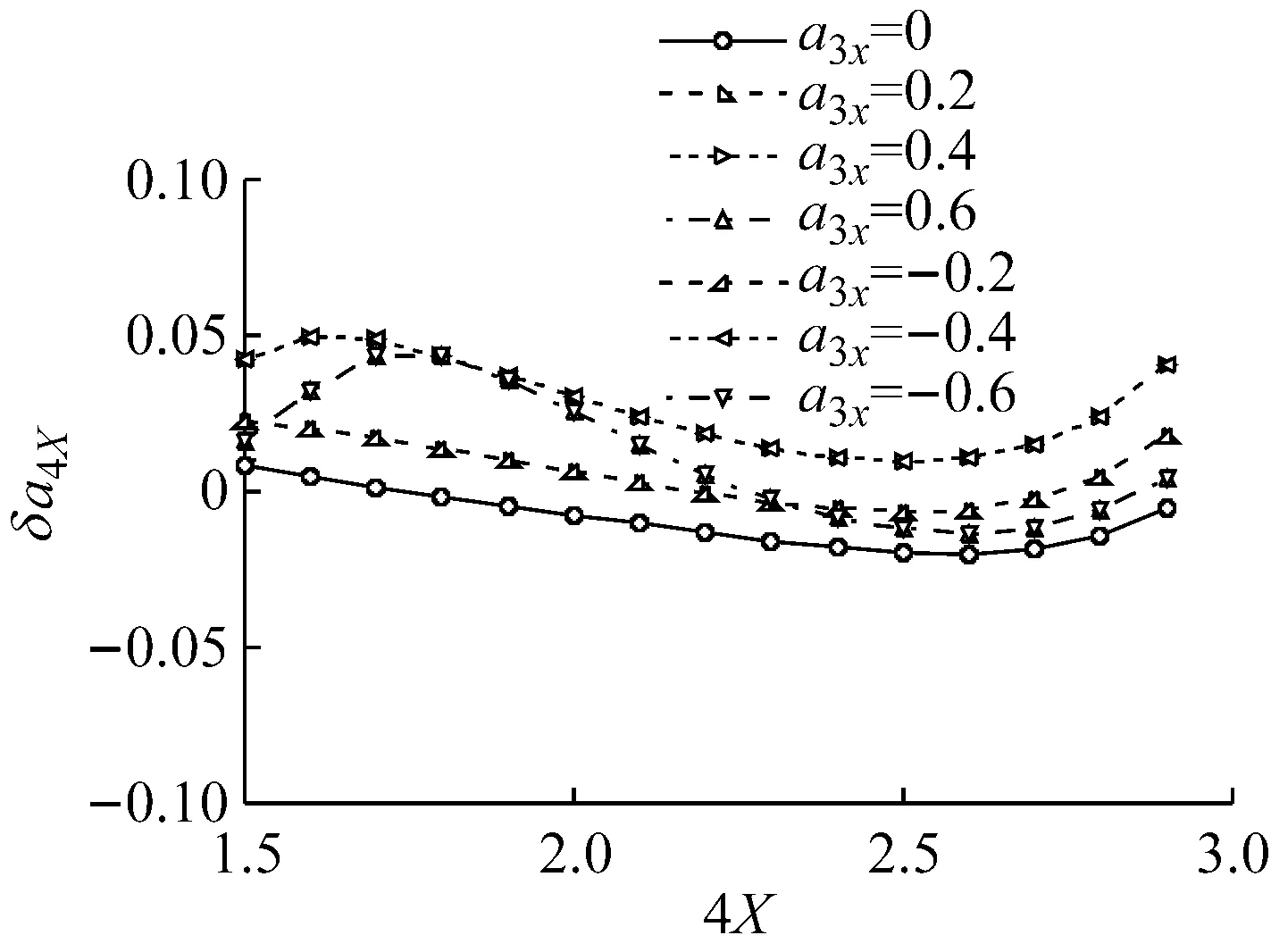
图3 Ding和Chen硬化模型峰度系数计算值与目标值误差

Fig.3 bias between the estimations based on Ding and Chen model and the target values for kurtosis

3 算例分析

3.1 转换模型的x-u变换

为了进一步调查Winterstein(1994)以及Ding和Chen模型的转换精度，选取两种分布：① Gamma分布(峰度系数=9>3)；② 截尾正态分布(峰度系数=2.794<3)进行分析。两种分布的参数及其四阶矩列于表1中。图4和图5分别对应了Gamma和截尾正态分布两种情况的x-u变换。在图4给出了利用Rosenblatt变换，Winterstein(1994)，Winterstein(1988) 多项式变换计算结果。图5给出了利用Rosenblatt变

换，Ding和Chen模型，Winterstein(1988)多项式变换计算结果。由于Rosenblatt变换[29]完全保留了边缘分布的信息，在此可以作为精确结果，用以作为已有转换模型比较的标准。从图4以及图5结果说明如下：

(1) 在图4中，随着xs的逐渐增大，使用Winterstein(1988)多项式计算的结果与Rosenblatt变换计算结果差异也逐渐变大。

(2) 在图5中，当xs的绝对值越来越大时，使用Winterstien(1988)多项式计算的结果与Rosenblatt变换计算结果差异也变大。

(3) 从图4及图5分别可以看出，Winterstien(1994)以及Ding和Chen计算结果基本与Rosenblatt变换结果重合，说明了Winterstien(1994)模型以及Ding和Chen模型转换的精度及有效性。

表1 概率分布及其前四阶矩

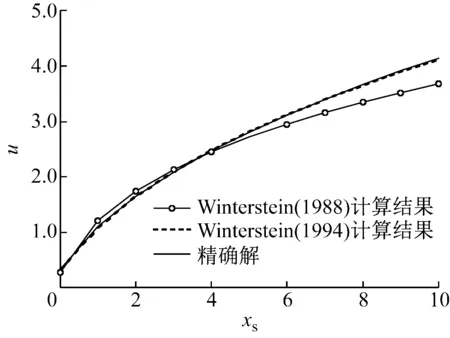
图4 Gamma分布的x-u变换

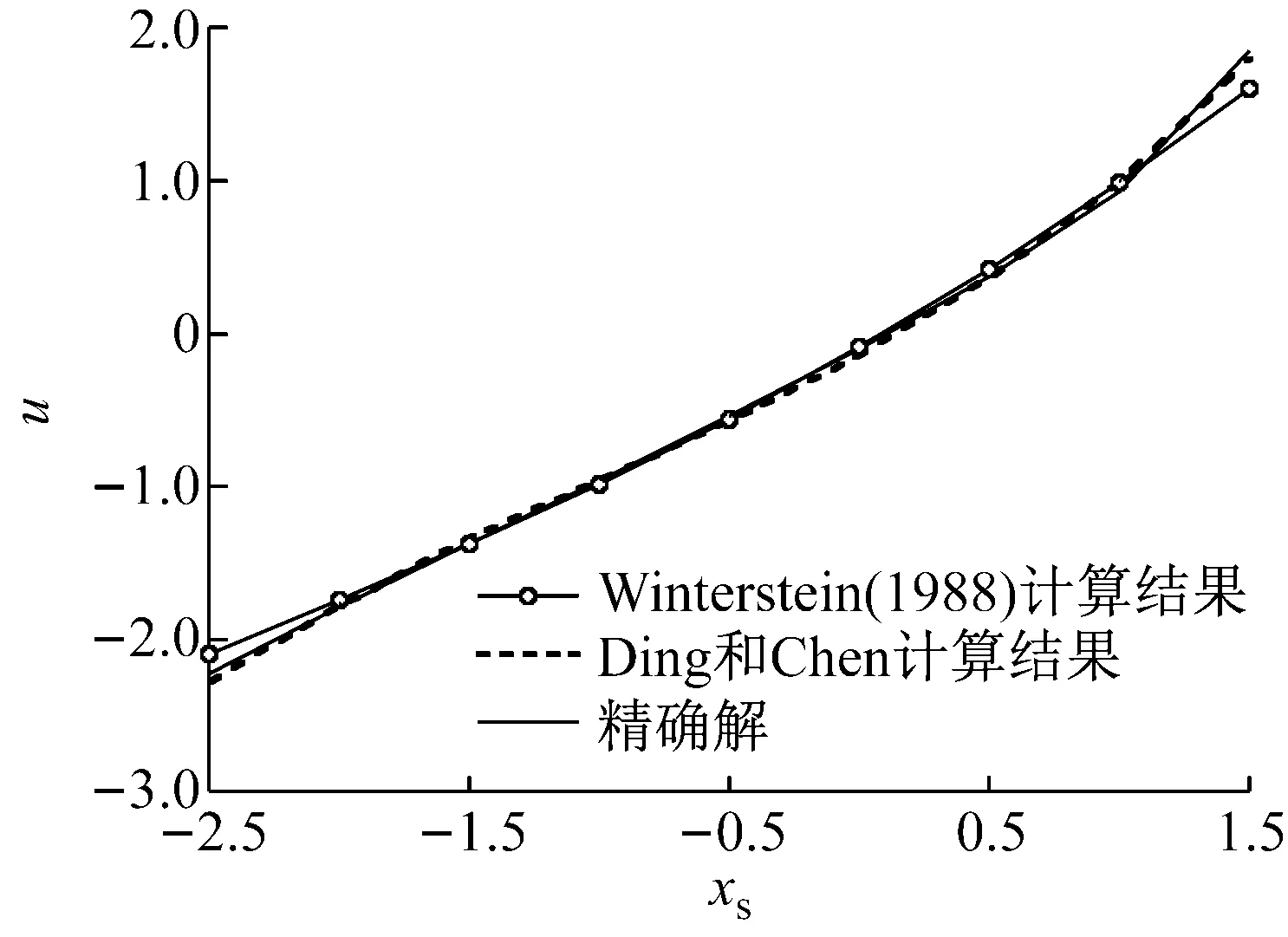
图5 截尾正态分布的x-u变换

3.2 平稳非高斯过程的首次穿越概率计算

选取线性与非线性单自由度系统为例，利用已有的He和Zhao模型，本文修正方法以及Monte Carlo模拟计算结构响应为软化反应(α4X>3)与硬化反应(α4X<3)的首次穿越概率，并进行对比分析。

例1结构响应为软化反应的首次穿越概率

二次力函数F(t)激励线性单自由度系统(SDOF)如图6所示。力函数F(t)=α1U(t)+α2U2(t)，其中U(t)代表一个平稳零均值的标准高斯过程，α1与α2是常数。

图6 二次力函数F(t)激励线性单自由度系统

Fig.6 A single-degree-of-freedom (SDOF) structure excited by a quadratic forcing functionF(t)

考虑阻尼比ζ=0.1和0.2两种情况，根据文献[30] 的方法，对于α2U2(t)激励部分的结构响应前四阶矩计算于表2中。从表2中可以看出在ζ=0.1和0.2两种情况下计算的结构响应为软化反应(α4X>3)。对应于表2的前四阶矩，在界限x=3σX情况下，采用本文修正方法(α4X>3的情况)计算的首次穿越概率如图7所示。同时，图中给出了由Monte Carlo模拟[31](10 000个样本)，He和Zhao方法和传统高斯模型计算结果。

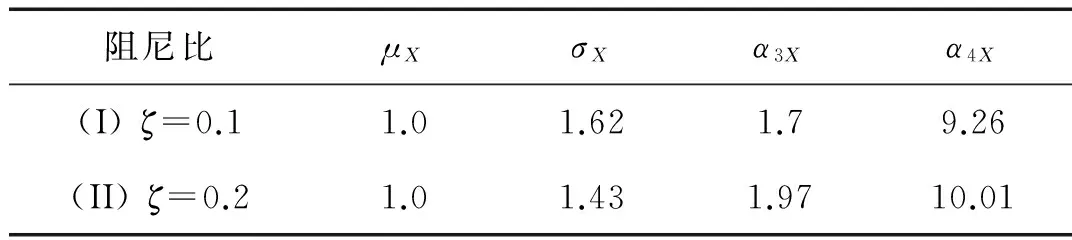
表2 平稳结构响应X(t)的前四阶矩

图7(a)和图7(b)计算结果表明：

(1) 传统高斯模型计算结果与Monte Carlo模拟结果有很大的差异，具有很大的保守性。

(2) 虽然He和Zhao模型相对于传统高斯模型有很大的提高，但是与Monte Carlo计算结果还有一些差距。这些误差产生的原因在于Winterstein多项式转换的精度不够。

(3) 本文修正的方法比较He和Zhao模型，以及传统高斯模型有很大的提高，在整个计算的时间段内均能与Monte Carlo模拟结果更为吻合。因此，对于软化反应，本文修正方法更为适用于首次穿越概率的计算。

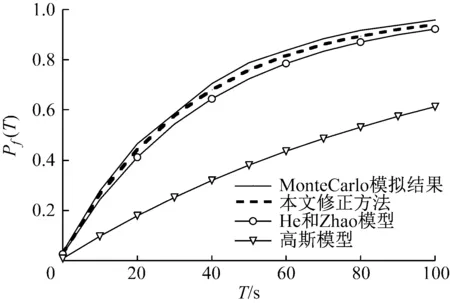
(a) ζ=0.1

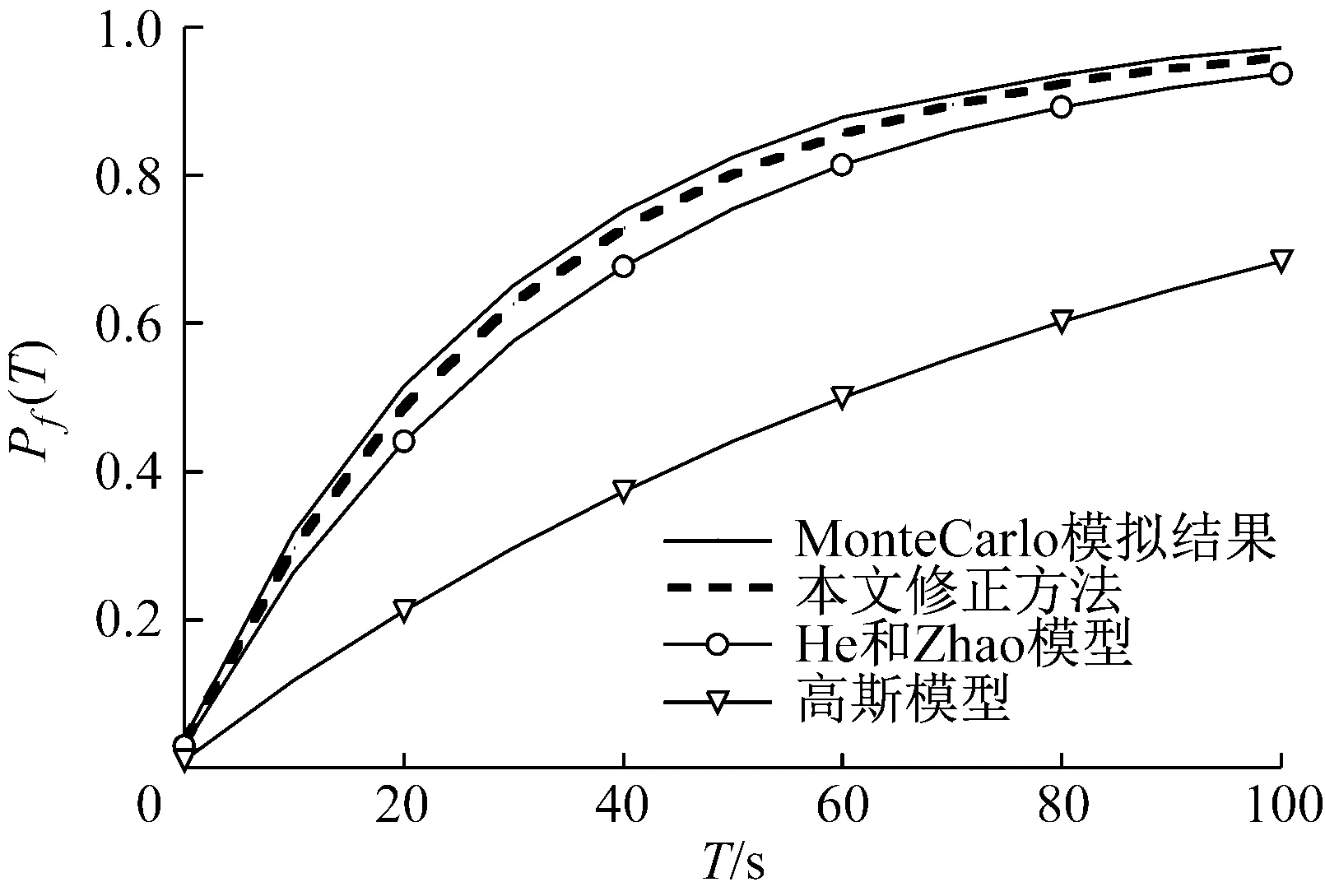
(b) ζ=0.2

例2结构响应为硬化反应的首次穿越概率

考虑平稳高斯白噪声激励Duffing振子的平稳响应。对于单边谱密度为1/π时，该振子的运动方程为

(18)

式中:c>0为阻尼系数;ε为控制系统的非线性参数。

Duffing振子的平稳概率密度函数f(X)有精确解[32]，可以表达为

(19a)

式中，

(19b)

式中:K1/4(·)是修正的Bessel函数1/4阶。

该概率密度函数f(X)说明X(t)是非高斯的。根据式(19a)和(19b)，计算得到位移反应的前四阶矩，结果及其相关参数列于表3中。从表3中可以看出该结构响应的峰度系数小于3，所以该结构响应为硬化反应。

表3结构参数及其位移响应的前四阶矩

Tab.3Thestructuralparametersandthefirstfourmomentsofdisplacement

式(18)的相关参数位移响应的前四阶矩μXσXα3Xα4Xω0=1rad/s,ε=0.1,c=0.201.3466702.47436

考虑界限水平x=2σX，利用本文修正方法、He和Zhao方法、传统高斯模型以及Monte Carlo模拟(10 000个样本)计算在[0,T]时段内的首次穿越概率。计算结果如图8所示。从图8中说明了结构在硬化非高斯结构响应下，本文修正的方法与Monte Carlo模拟结果拟合最好，而其余两种方法均有不同的差异。因此，本文修正的方法也适用于硬化反应的首次穿越概率计算。

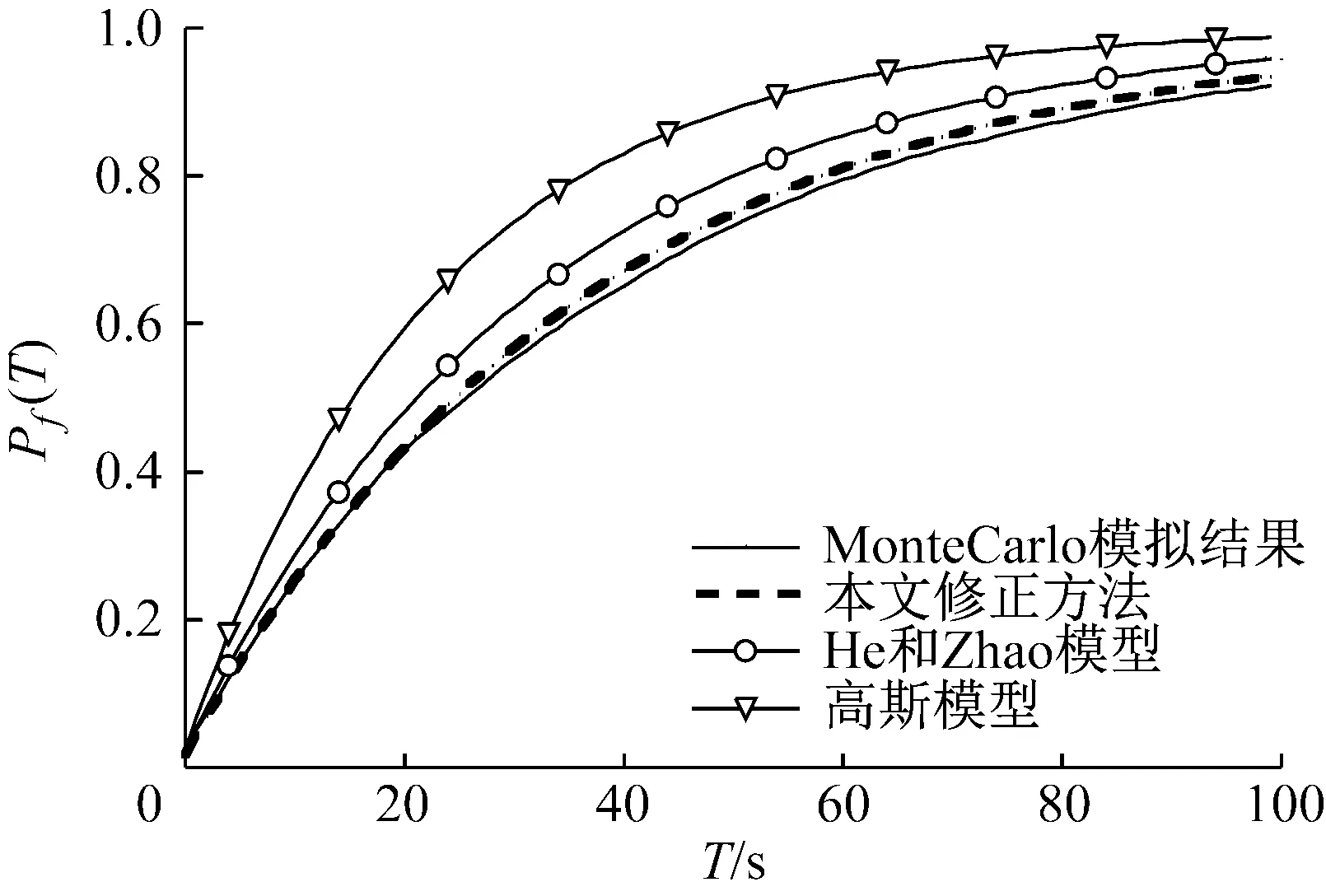
图8 界限水平为x=2σX的首次穿越概率

4 结 论

本文基于平稳高斯结构响应的Poisson模型修正了一个平稳非高斯结构响应(软化与硬化)的首次穿越概率的解析方法。在软化与硬化的非高斯结构响应中，基于结构响应的前四阶矩，分别采用Winterstein(1994)模型，Ding和Chen模型的等效高斯分位数及非高斯结构响应的界限水平将平稳非高斯结构响应映射为标准高斯过程。接着，利用考虑初始条件与群超效应的平稳高斯结构响应的Poisson模型计算首次穿越概率。

通过分析Winterstein(1994)软化模型、Ding和Chen硬化模型的转换精度及适用情况，验证了模型运用于平稳非高斯结构响应的首次穿越概率计算的准确性与适用性。通过线性与非线性单自由度系统算例分析，说明了本文修正的方法计算结果比其他已有解析方法能更好地与Monte Carlo模拟结果吻合,同时进一步验证了本文修正的方法更适用于软化与硬化平稳非高斯结构响应的首次穿越概率计算。

[1] 李桂青，李秋胜. 工程结构时变可靠度理论及其应用[M]. 北京：科学出版社，2001.

[2] RICE S O. Mathematical analysis of random noise[J]. Bell System Technical Journal, 1944, 23(3): 282-332.

[3] RICE S O. Mathematical analysis of random noise. Part III: Statistical properties of random noise currents[J]. Bell System Technical Journal, 1945, 24(1): 46-156.

[4] COLEMAN J J. Reliability of aircraft structures in resisting chance failure [J]. Operations Research, 1959, 7(5): 639-945.

[5] 刘佩. 基于贝叶斯理论的结构动力可靠度更新方法与分析[J]. 振动与冲击，2015，34(12)：29-34.

LIU Pei. Structural dynamic reliability updating method based on Bayesian theorem [J]. Journal of Vibration and Shock, 2015, 34(12): 29-34.

[6] VANMARCKE E H. On the distribution of the first passage time for normal stationary process [J]. Journal of Applied Mechanics, 1975, 42(1): 215-220.

[7] 陈建兵，李杰. 非线性随机地震响应的概率密度演化分析[J]. 武汉理工大学学报，2010，32(9)：6-10.

CHEN Jianbing, LI Jie. Probability density evolution analysis for stochastic seismic response of nonlinear structures [J]. Journal of Wuhan University of Technology, 2010, 32(9):6-10.

[8] CRANDALL S H. First-crossing probabilities of the linear oscillator [J]. Journal of Sound and Vibration, 1970, 12(3): 285-299.

[9] NAESS A. Approximate first-passage and extremes of narrow-band Gaussian and non-Gaussian random vibrations [J]. Journal of Sound and Vibration, 1990, 138(3): 365-380.

[10] BARBATO M, CONTE J P. Structural reliability applications of nonstationary spectral characteristics [J]. Journal of Engineering Mechanics, 2011, 137(5): 371-382.

[11] GHAZIZADEH S, BARBATO M, TUBALDI E. New analytical solution of the first-passage reliability problem for linear oscillators [J]. Journal of Engineering Mechanics, 2012, 138(6):695-706.

[12] GRIGORIU M. Crossings of non-Gaussian translation processes [J]. Journal of Engineering Mechanics, 1984, 110(4): 610-620.

[13] OCHI M. Non-Gaussian random processes in ocean engineering [J]. Probabilistic Engineering Mechanics, 1986, 1(1): 28-39.

[14] JOHNSOM N L, KOTZ S. Continuous univariate distribution-1 [M]. Boston: Houghton Mifflin Company, 1970.

[15] WINTERSTEIN S R. Nonlinear vibration models for extremes and fatigue [J]. Journal of Engineering Mechanics, 1988, 114(10): 1772-1790.

[16] HE J, ZHAO Y G. First passage times of stationary non-Gaussian structural responses [J]. Computers and Structures, 2007, 85(7/8): 431-436.

[17] ZHAO Y G, LU Z H. Fourth-moment standardization for Structural Reliability Assessment [J]. Journal of Structural Engineering, 2007, 133(7): 916-924.

[18] CHOI M, SWEETMAN B. The Hermite moment model for highly skewed response with application to tension leg [J]. Journal of Offshore Mechanics and Arctic Engineering, 2010, 132(2): 1-8.

[19] HUANG M F, LOU W J, CHAN C M, et al. Peak distribution and peak factors of wind-induced pressure processes on tall buildings [J]. Journal of Engineering Mechanics, 2013, 139 (12): 1744-1756.

[20] WINTERSTEIN S R, UDE T C, KLEIVEN G. Springing and Slow-Drift Responses: Predicted Extremes and Fatigue vs. Simulation [C]//BOSS-94. Cambrige: Massachusetts Institute of Technology, 1994: 1-15.

[21] DING J, CHEN X. Moment-based translation model for hardening non-Gaussian response processes [J]. Journal of Engineering Mechanics, 2016, 142(2): 1-7.

[22] DITLEVSEN O. Duration of visit to critical set by Gaussian process [J]. Probabilistic Engineering Mechanics, 1986, 1(2): 82-93.

[23] HE J. Approximate method for estimating extreme value responses of nonlinear stochastic dynamic systems [J]. Journal of Engineering Mechanics, 2015, 141(7): 1-9.

[24] LANGLEY R S. A first passage approximation for normal stationary random processes [J]. Journal of Sound Vibration, 1988, 122(2): 261-275.

[25] WINTERSTEIN S R, KASHEF T. Moment-based load and response models with wind engineering applications [J]. Journal of Solar Energy Engineering, 2000, 122(3): 122-128.

[26] WINTERSTEIN S R, MACKENZIE C A. Extremes of nonlinear vibration: comparing models based on moments, L-moments, and maximum entropy [J]. Journal of Offshore Mechanics Arctic Engineering, 2011, 135(2): 185-195.

[27] FLEISHMAN A L. A method for simulation non-normal distributions [J]. Psychometrika, 1978, 43(4):521-532.

[28] ZHAO Y G, LU Z H. Cubic normal distribution and its significance in structural reliability [J]. Structural Engineering and Mechanics, 2008, 28(3):263-280.

[29] HOHENBICHLER M, RACKWITZ R. Zon-normal dependent vectors in structural safety[J]. Journal of Engineering Mechanics Division, 1981, 107(6): 1227-1238.

[30] NAESS A. The response statistics of nonlinear, second order transformations to Gaussian loads [J]. Journal of Sound and Vibration, 1987, 115(1): 103-129.

[31] BAYER V, BUCHER C. Importance sampling for first passage problems of nonlinear structures [J]. Probabilistic Engineering Mechanics, 1999, 14(1/2): 27-32.

[32] SONG T T, GRIGORIU M. Random vibration of mechanical and structural systems [M]. Englewood Cliffs, NJ: Prentice Hall, 1993.