结合VMD和Volterra预测模型的轴承振动信号特征提取
2018-02-27张云强张培林王怀光杨玉栋吴定海
张云强, 张培林, 王怀光, 杨玉栋, 吴定海
(1. 军械工程学院 车辆与电气工程系,石家庄 050003; 2. 武汉军械士官学校 四系,武汉 430075)
滚动轴承是旋转机械中常见的精密零件之一,也是经常损坏的元件之一。研究表明,在使用滚动轴承的旋转机械中,约30%的机械故障是由滚动轴承发生故障直接或间接引起的,给工业生产和生活造成巨大经济损失[1-2]。因此,开展滚动轴承状态识别与故障诊断意义重大。当轴承出现故障时,其振动信号具有明显的非线性和非平稳性,蕴含着大量的轴承故障信息。如何从这些信号中提取有效特征参数是轴承故障诊断亟待解决的问题。
轴承振动信号本质是与轴承健康状态相关的时间序列。时间序列的参数化建模可以根据系统动态数据建立准确反映数据所蕴含动态关系的数学模型,从而揭示系统结构和规律。其中自回归(Auto Regressive,AR)模型和自回归滑动平均(Auto Regressive and Moving Average Model,ARMA)模型是应用最广泛的两个时间序列模型。赵联春等[3]对轴承振动信号信号分析中的AR模型进行了深入研究;孙学斌[4]利用AR模型对机床轴承振动信号进行建模,从而实现了轴承故障诊断;刘颖等[5]结合ARMA模型和聚类分析提取了轴承振动信号特征参数,达到了轴承故障类型的准确识别的目的。虽然AR模型和ARMA模型在轴承故障诊断中取得了较好的效果,但是二者均是线性预测模型,在对时间序列建模时,常常假设信号是平稳的,导致在处理非线性和非平稳的轴承故障信号时容易产生较大的误差,从而影响轴承故障诊断精度[6-7]。
为了解决上述问题,一些学者引入经验模态分解(Empirical Mode Decomposition, EMD)[8]和Volterra预测模型。EMD能够依据信号本身的特性,将非平稳信号分解为若干个平稳的本征模式函数(Intrinsic Mode Function, IMF)分量。Volterra模型是一种非线性预测模型,广泛应用于工程中的非线性系统建模。Cheng等[9-10]提出了一种基于EMD和AR模型的滚动轴承故障诊断方法,缓解了AR模型在非平稳信号建模中的不足;陈冬青等[11]结合ARMA模型与EMD提取了轴承振动信号的关联维数,提高了轴承损伤评定精度;Tang等[12]深入研究了Volterra模型在轴承故障诊断中的应用,取得了比AR模型更好的效果;裘焱等[13]在EMD分解的基础上对各分量建立Volterra模型,实现了非线性和非平稳信号的故障特征提取。然而,EMD缺乏严格的数学基础,对信号中的噪声比较敏感,容易产生严重的频率混叠现象,给轴承故障特征提取带来新的问题。
变分模式分解(Variational Mode Decomposition, VMD)[14]是一种新的自适应时频分析理论。与EMD相比,该理论采用完全非递归的方式实现信号的频域分解,具有分解能力强、抗噪性能好和处理速度快等特点[15-17]。因此,本文提出一种结合VMD和Volterra预测模型的滑动轴承振动信号特征提取方法,利用VMD将轴承振动信号分解成有限个平稳的IMF分量,在重构相空间内对各IMF分量采用Volterra预测模型进行非线性建模,并通过类内类间距准则对模型参数进行优选,用于准确描述轴承故障信号的非线性和非平稳性特征。
1 变分模式分解
1.1 变分模式分解理论
变分模式分解是建立在Wiener滤波、希尔伯特变换、解析信号、频率混合和外差解调等概念基础上的一种新的自适应时频分析方法,具有严格的数学基础,其分解过程本质上是一个特殊变分模型的迭代求解过程。
在建立信号分解的变分模型之前,VMD理论摒弃了EMD理论中IMF的定义,而将IMF进行了重新定义,即信号的IMF分量均是调幅-调频信号,如式(1)所示。
uk(t)=Ak(t)cos(φk(t))
(1)
式中:uk(t)为第k个IMF分量;Ak(t)和φk(t)分别为uk(t)的瞬时幅值和相位;φk(t)为非减函数,即瞬时频率ωk(t)=dφk(t)/dt≥0。与φk(t)相比,Ak(t)和ωk(t)的变化比较缓慢,即在较短的时间范围内可以认为是幅值和频率不变的谐波信号。
在上述定义基础上,VMD理论假设输入信号信号x(t)是由有限个带宽有限、中心频率不同的IMF组成,在各IMF分量之和等于输入信号x(t)的约束下,以寻求每个本征模态函数分量的估计带宽之和最小为目标构建信号分解的变分模型。变分模型的建立过程如下:
(1) 希尔伯特变换。对每个IMF分量进行希尔伯特变换,并为获得uk(t)的单边频谱,构造解析信号
*uk(t)
(2)
(2) 频率混合。给各IMF分量的解析信号混合一个预先估计的中心频率e-jωkt,从而将每个IMF分量的频谱移动到基频带上,即
(3)
(3) 带宽估计。通过计算式(3)所示解调信号梯度的L2范数,估计各IMF分量的带宽。
(4) 建立最优化模型。引入约束条件,构建如下最优化变分模型
(4)
式中:K为IMF分量个数;{uk}={u1,u2,…,uK},{ωk}={ω1,ω2,…,ωK}表示uk的频率中心。
为了对上述变分模型进行求解,VMD首先引入二次惩罚因子α和拉格朗日乘子λ(t),构造式(5)所示的扩展拉格朗日函数L({uk},{ωk},λ),将约束问题转化为非约束问题。其中α可以在含高斯噪声的情况下保证信号的重构精度,λ(t)可以确保模型约束条件的严格性。然后,利用乘法算子交替方向法(Alternating Direction Method of Multipliers,ADMM),交替迭代更新{uk}、{ωk}和λ,搜索扩展拉格朗日函数的鞍点,即为式(4)所示变分模型的最优解,从而将输入信号x(t)分解为K个带宽有限的IMF分量。变分模型的具体求解流程如图1所示。初始化时,{uk}、{ωk}和λ均取值为0。
L({uk},{ωk},λ)=
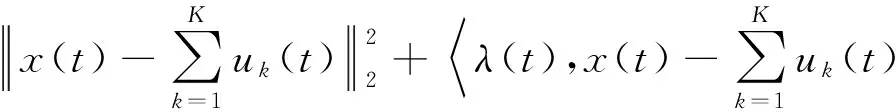
(5)
1.2 仿真信号分析
为了分析变分模式分解的信号分解能力,构造仿真信号x(t),如式(6)所示。
x(t)=x1(t)+x2(t)+x3(t)+sn(t)
(6)
式中:x1(t)、x2(t)和x3(t)分别为频率为10 Hz、50 Hz和75 Hz的正弦谐波信号,x1(t)和x3(t)的幅值为1,x2(t)的幅值为1.5;sn(t)为幅值为0.05的随机白噪声。设置信号的采样频率为4 096 Hz,采样时间为0.5 s,则仿真信号x(t)及其各分量的时域波形如图2所示。
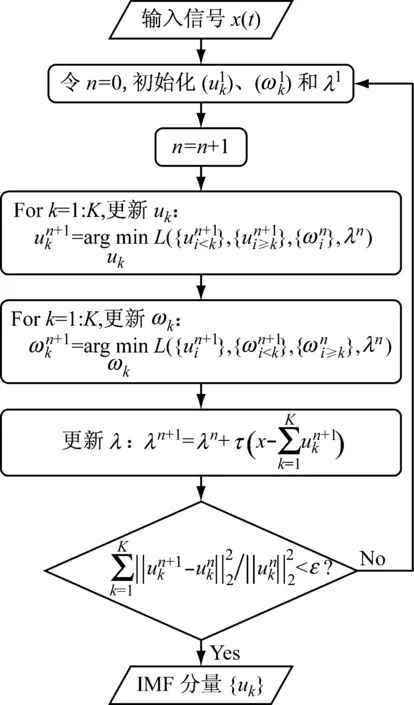
图1 变分模型求解流程图




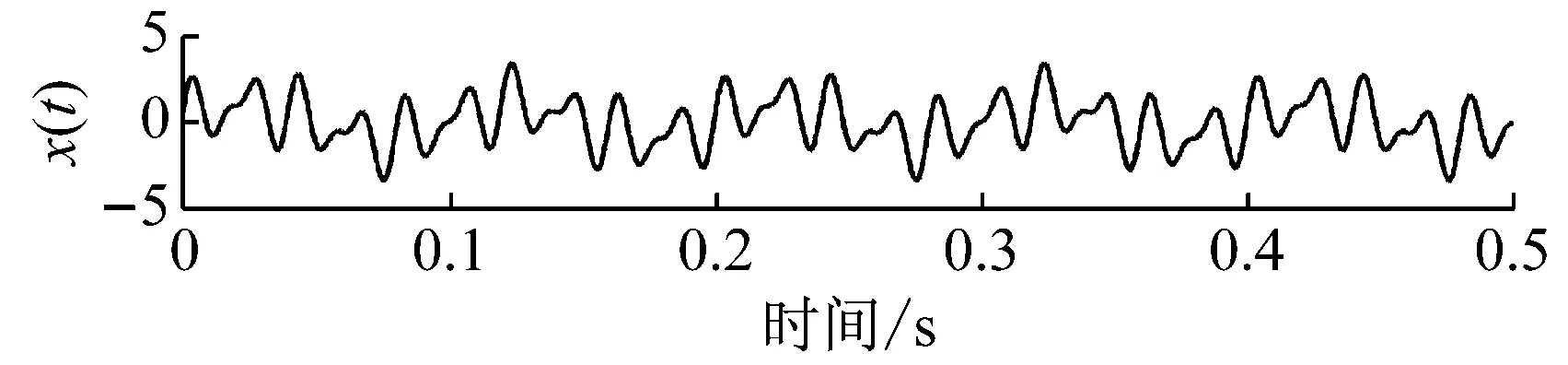
图2 仿真信号及其各分量时域波形
图3为仿真信号的EMD分解结果。由图3可知,EMD将仿真信号分解成7个IMF分量和1个残余分量。其中,IMF1分量主要是随机白噪声;IMF5与10 Hz正弦谐波分量有较好的对应关系;IMF2和IMF3分量虽然与50 Hz和75 Hz两个正弦谐波分量对应,但是EMD无法将两个正弦谐波分量进行有效分离,产生了严重的频率混叠现象,并且受噪声干扰,波形也出现了明显失真;IMF4、IMF6、IMF7和R4个分量与仿真信号没有较好的对应关系,是信号分解时产生的虚假分量。


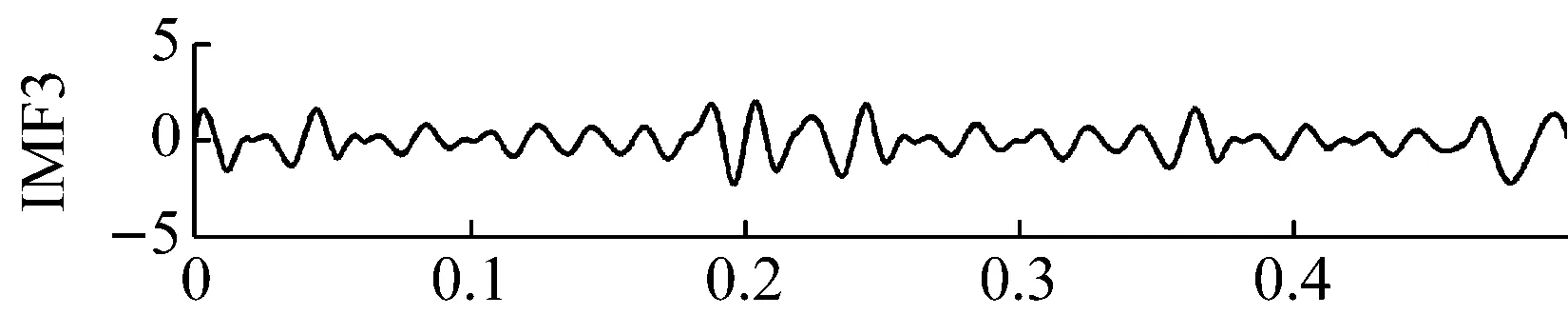




图3 仿真信号EMD分解结果
选择K=4,α=2 000,采用VMD对仿真信号x(t)进行分解,结果如图4所示。由图4可知,VMD能准确地把仿真信号的3个正弦谐波分量和1随机白噪声分量很好地分离开,其中IMF1、IMF2和IMF3分别与正弦谐波分量x1(t)、x2(t)和x3(t)对应,IMF4与随机白噪声分量对应。
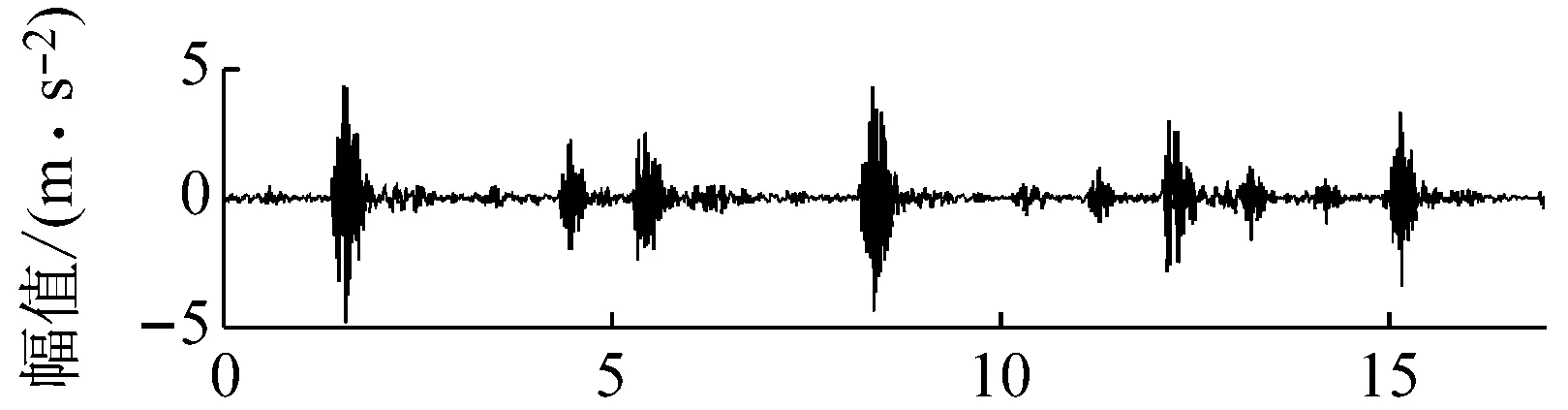
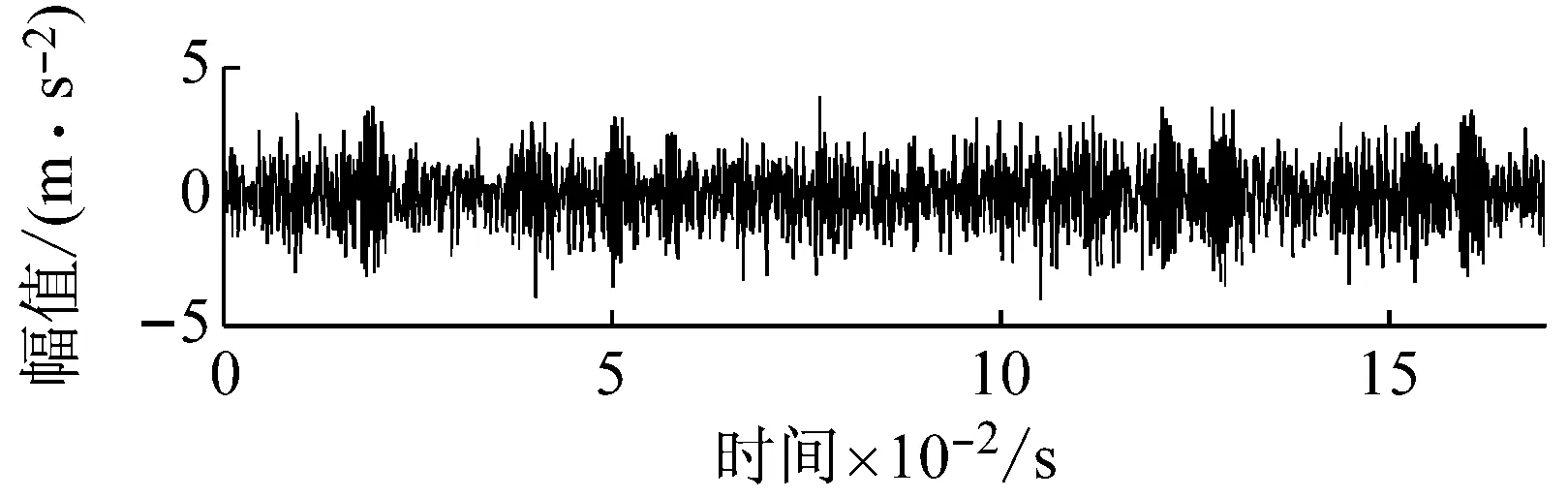
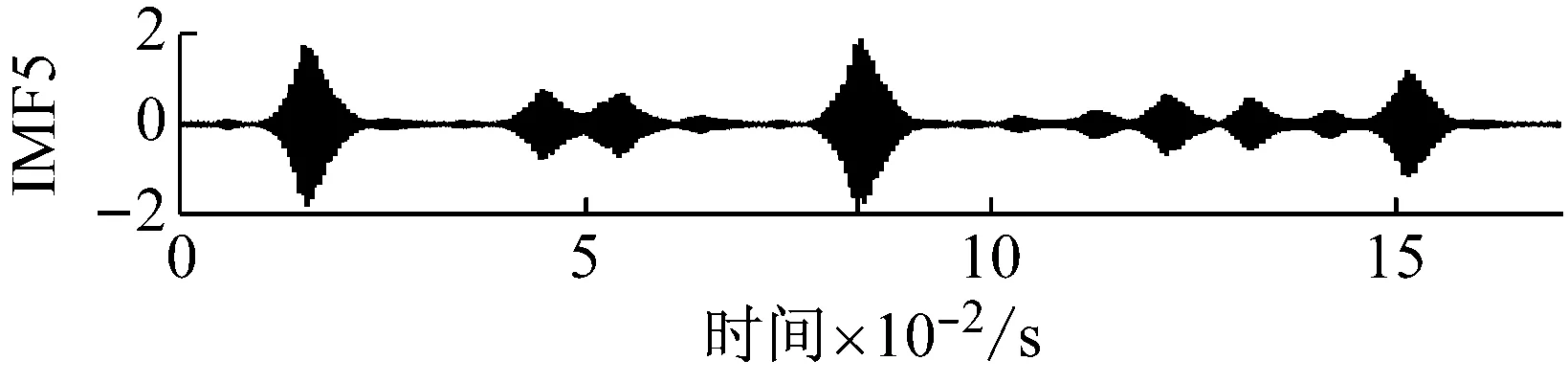
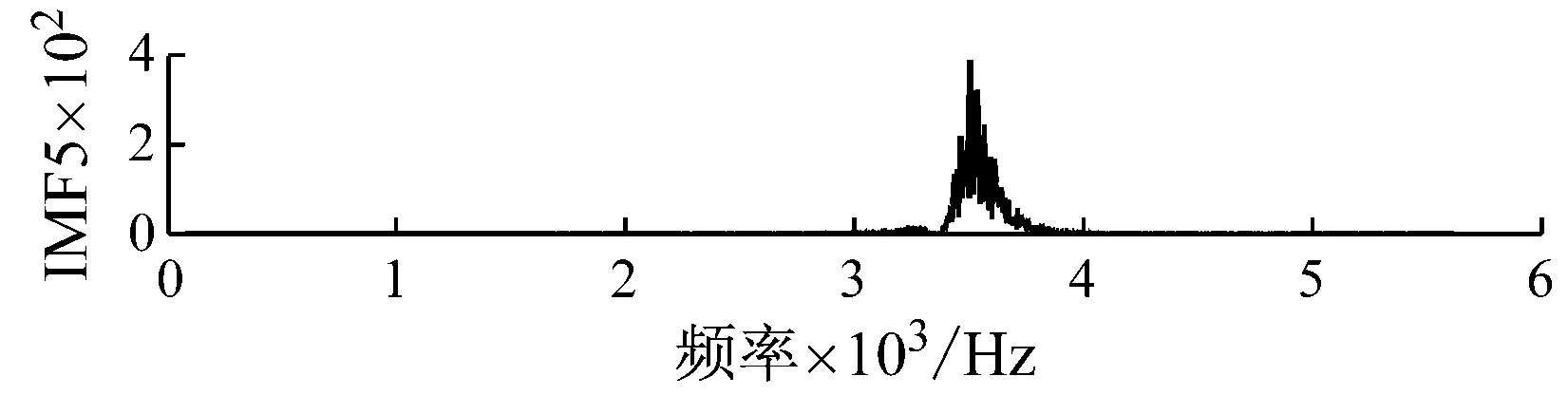
对比EMD和VMD分解结果可知,由于EMD的抗噪性能较差,且对频率满足f1 图4 仿真信号VMD分解结果 相空间重构是建立Volterra预测模型的基础。对于一个单输入单输出的非线性离散系统,假设系统的输入为时间序列x(1),x(2),…,x(n),可以采用Takens等提出的延迟坐标法对系统进行相空间重构[18]。该重构相空间中的点可以描述为 X(n)=[x(n),x(n-τ),…,x(n-(m-1)τ)] (7) 式中:m和τ分别为系统嵌入维数和时间延迟。 Takens定理表明,若系统嵌入维数m≥2d+1,d为系统的动力学维数,则相空间重构的系统与原系统在拓扑意义上是等价的,2个相空间中的混沌吸引子具有微分同胚的性质。因此,利用相空间重构理论和非线性系统的当前状态,可以预测系统下一时刻的状态,这为时间序列预测提供了理论基础。 系统嵌入维数和时间延迟参数的估计是相空间重构的关键。目前,可同时估计该两个参数的方法有C-C方法和时间窗口法等。C-C方法具有计算简单、估计准确和抗噪性能好等优点,因此本文在相空间重构时采用C-C方法估计系统的嵌入维数m和时间延迟参数τ。 时间序列预测本质上是一个动力系统的逆问题,即根据动力系统的状态构建系统的动力学模型F y(n)=x(n+T)=F(X(n)) (8) 式中:T>0为向前预测步长。 Volterra模型是一种非线性预测模型,能够很好地逼近模型F,广泛应用于工程中的非线性系统建模。若非线性系统的输入为X(n)、输出为y(n),则该系统的Volterra级数展开式为 (9) 式中:hk(i1,i2,…,ik)为k阶Volterra核;p为级数的阶数;M为记忆长度。Volterra级数属于无穷级数,实际应用比较困难。由于工程上大部分非线性系统都可用二阶的Volterra级数来描述[19],本文选择二阶的Volterra级数构建时间序列预测模型,即 (10) 令W(n)=[h0,h1(0),h1(1),…,h1(M-1),h2(0,0),h2(0,1),…,h2(M-1,M-1)]T,Z(n)=[1,x(n),x(n-τ),…,x(n-(M-1)τ),x2(n),x(n)x(n-τ),…,x2(n-(M-1)τ)]T,则式(10)可以改写为 y(n)=ZT(n)W(n) (11) 利用归一化最小均方自适应算法对式(11)进行求解,即获得时间序列的Volterra预测模型,实现对模型F的非线性逼近。模型参数向量W(n)蕴含着系统状态的重要信息,是系统故障诊断的重要依据。 采用VMD对滚动轴承振动信号进行分解后,每个IMF分量代表着轴承信号不同频率成分,信号的特征完全可以由K个IMF分量来描述。Volterra预测模型如同一个信息凝聚器,采用该模型对各IMF分量进行非线性建模,可将IMF分量蕴含的信息都凝聚于模型参数向量中。因此,通过对K个IMF分量的Volterra模型参数向量进行优选,就可以获得用于描述轴承振动信号非线性和非平稳特性的特征参数。 结合VMD和Volterra预测模型的特征取方法实现步骤如下: 步骤1利用最大相关最小冗余准则[20]自动选取VMD中的参数K,然后对每一个轴承振动信号x(t)进行VMD自适应分解,得到K个IMF分量uk(t); 步骤2采用C-C方法估计各IMF分量uk(t)的嵌入维数m和时间延迟参数τ,并对uk(t)进行相空间重构; 步骤3选取记忆长度M=m,在重构相空间中对uk(t)建立二阶Volterra自适应预测模型; 步骤4依据式(12)所示的类内类间距准则对模型参数进行优选,Jb越大表明对应模型参数的区分性能越好,从而得到描述轴承振动信号的特征参数。 (12) 式中:Sb和Sw分别为类内散度和类间散度。 实验所用的滚动轴承振动信号采自于一个单级传动齿轮箱振动试验系统。该系统主要由台架基座、调速电机、单级传动齿轮箱、磁粉阻尼器、联轴器、振动传感器和数据采集设备等组成。采用的传感器型号为B&K4508振动加速度传感器,安装在测试轴承座正上方的箱体表面。测试轴承为SKF6205深沟球轴承,安装在调速电机输出轴上,试验采用电火花加工的方式分别于测试轴承的外圈、内圈和滚动体上加工深度为0.053 mm的凹槽来模拟轴承的3种常见的单点故障。试验载荷为2.2 kW,采样频率为12 kHz。图5为采集的4种不同状态的轴承振动信号。 以轴承外圈故障信号为例进行分析。根据最大相关最小冗余准则,选取K=5,对图5中轴承外圈信号进行VMD分解。 (a) 正常 (b) 外圈故障 (c) 内圈故障 (d) 滚动体故障 图6和图7分别展示了VMD分解结果的时域波形和频谱。观察图6和图7可知,VMD将轴承外圈故障信号分解成了5个不同频率成分IMF分量,各分量相互独立,不存在模态混叠的现象。 图6 VMD分解结果时域波形 图7 VMD分解结果的频谱 作为对比,图8给出了轴承外圈故障信号的EMD分解结果。由图8可以看出,EMD将外圈故障信号分解成了7个IMF分量和1个残余分量。IMF2与IMF3、IMF4与IMF5均存明显的频率混叠现象;IMF6、IMF7和R3个分量与原信号联系较小,是分解出的虚假分量。 与VMD分解结果相比,EMD的分解结果较差,VMD具有较好的轴承信号分解能力,更加适合于轴承振动信号分解。 选择记忆长度M=m=3,对所有轴承振动信号的IMF分量在重构的相空间中建立二阶Volterra自适应预测模型。由于二阶Volterra自适应预测模型的参数向量W(n)有10个元素,每一个轴承振动信号会产生10×5=50个模型参数。为引入对比,对各轴承振动信号EMD分解结果的前5个IMF分量也建立二阶Volterra自适应预测模型。 图8 EMD分解结果时域波形 图9为类内类间距准则函数Jb由大到小随模型参数的变化情况。对比VMD与EMD对应的两条曲线可知,除前3个和后9个模型参数的区分性能相当以外,VMD的中间38个模型参数的区分性能优于EMD。此外,VMD对应的曲线中Jb>0.9的有11个参数,而EMD仅有5个。由此说明,不同模型特征参数具有不同的轴承状态区分能力,采用VMD分解得到的模型参数的区分性能明显优于EMD。 取Jb>0.9,对经VMD分解得到Volterra模型参数进行选择,最终提取出的Volterra模型特征如表1所示,表中每种轴承状态包含2个样本,模型参数符号上标代表IMF分量序号。观察图9可知,所提特征参数具有很好的类内聚合性和类间分散性,为轴承故障准确诊断奠定了良好基础。 图9 模型特征参数性能比较 模型参数h51(1)h31(1)h51(0)h41(0)h41(2)h51(2)h11(1)h21(0)h21(2)h21(0)h31(2)正常外圈故障内圈故障滚动体故障-0.78693.3512-2.4403-0.0121-0.69191.06230.2144-0.48880.25480.13341.4935-0.78633.1072-2.7276-0.0169-0.69491.05670.2168-0.48730.2625-0.08061.4952-1.4955-0.8800-0.0979-0.2016-0.57380.41520.0281-0.69850.1103-0.41531.3393-1.4913-0.8755-0.1047-0.2124-0.57370.42130.0241-0.69950.1105-0.42881.3430-0.59330.34240.0072-0.0755-0.58470.25790.0279-0.78480.0451-0.11221.3562-0.59540.34660.0114-0.0647-0.58710.23460.0203-0.80800.0525-0.04391.3590-1.0167-0.7608-0.1015-0.0521-0.53090.54210.2311-0.52910.06420.03231.2805-1.0242-0.7234-0.0845-0.0562-0.53110.53820.2379-0.52670.04800.08951.2657 为测试所提特征参数在滚动轴承故障诊断中的效果,从4种状态的滚动轴承信号中分别随机选取20个样本构造训练集,剩余20个样本构造测试集,采用K近邻分类器(K-Nearest Neighbor Classifier,K-NNC)、朴素贝叶斯分类器(Naive Bayes Classifier,NBC)和支持向量机(Support Vector Machine,SVM)分别对滚动轴承振动信号进行分类。在K-NNC分类时,取K=1;在SVC分类时,采用径向基核函数和“一对一”策略构建多类分类器,并通过交叉验证的方法自动选择参数。同时,选取经EMD分解的Volterra模型参数中Jb>0.9的特征参数构造对比实验。为了降低实验结果的随机性,实验重复5次,每次参与实验的样本均重新随机选取。表2给出了5次实验的平均分类结果。 表2 滚动轴承振动信号分类结果 由表2可以看出,采用不同分类器进行分类时,结合VMD分解提取的模型参数的分类精度达最高达到98.00%,最低达到95.25%,而结合EMD分解提取的模型参数的分类精度最高分类精度仅为93.00%;就相同分类器而言,结合VMD分解提取的模型参数的分类效果均优于结合EMD分解提取的模型参数。分类结果表明,与EMD相比,结合VMD提取的Volterra模型特征能更准确地对滚动轴承故障进行诊断。 针对非线性、非平稳的滚动轴承振动信号,提出了一种结合变分模式分解和Volterra预测模型的滚动轴承振动信号特征提取方法。该方法利用变分模式分解将轴承振动信号自适应地分解为有限个平稳的IMF分量,进而对各IMF分量建立Volterra自适应预测模型,采用类内类间距准则对模型参数进行优选,从而提取振动信号的Volterra模型参数。实验结果表明,结合变分模式分解提取的Volterra模型特征能有效表达振动信号的非线性和非平稳特性,从而提高滚动轴承故障诊断精度。 [1] 徐振辉, 马立元. 滚动轴承的故障特征提取[J]. 兵工自动化, 2004, 23(1): 46-48. XU Zhenhui, MA Liyuan. Picking up fault character of rolling bearings[J]. Ordnance Industry Automation, 2004, 23(1): 46-48. [2] 王宏超, 陈进, 董广明. 基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取[J]. 机械工程学报, 2013, 49(1): 88-94. WANG Hongchao, CHEN Jin, DONG Guangming. Fault diagnosis method for rolling bearing’s weak fault based on minimum entropy deconvolution and sparse decomposition[J]. Journal of Aechanical Engineering, 2013, 49(1): 88-94. [3] 赵联春, 马家驹, 范树迁,等. 滚动轴承振动分析中的AR模型研究[J]. 中国机械工程, 2004, 15(3): 210-213. ZHAO Lianchun, MA Jiaju, FAN Shuqian, et al. Research on AR model in vibration analysis of rolling bearing[J]. China Mechanical Engineering, 2004, 15(3): 210-213. [4] 孙学斌. AR模型和SVM在机床滚动轴承故障诊断中的应用[J]. 机械工程与自动化, 2010, 44(2): 132-134. SUN Xuebin. Application of AR model and SVM in machine rolling bearing fault diagnosis[J]. Mechanical Engineering & Automation, 2010, 44(2): 132-134. [5] 刘颖, 严军. 基于时间序列ARMA模型的振动故障预测[J]. 化工自动化及仪表, 2011, 38(7): 841-843. LIU Ying, YAN Jun. Vibration faults prediction based on time series auto regressive moving average(ARMA) model[J]. Control and Instruments in Chinese Industry, 2011, 38(7): 841-843. [6] 范庚, 马登武. 基于EMD和RVM-AR的航空发动机磨损故障预测模型[J]. 计算机测量与控制, 2013, 21(3): 1746-1749. FAN Geng, MA Dengwu. Aero-engine wear faults prediction based on EMD and RVM-AR[J]. Computer Measurement & Control, 2013, 21(3): 1746-1749. [7] 王俨剀, 马进锐, 廖明夫,等. 发动机振动趋势预测模型研究[J]. 振动、测试与诊断, 2014, 34(3): 517-523. WANG Yankai, MA Jinrui, LIAO Mingfu, et al. Research on trend prediction model of engine vibration[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(3): 517-523. [8] HUANG N E, SHEN Z, LONG S R, et al. The empirical model decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Processing of Royal Society of London A, 1998, 454: 903-995. [9] CHENG Junsheng, YU Dejie, YANG Yu. A fault diagnosis approach for roller bearings based on EMD method and AR model[J]. Mechanical System and Signal Processing, 2006, 20(2): 350-362. [10] 孟宗, 顾海燕. 应用经验模态分解下的AR模型提取旋转机械故障特征[J]. 燕山大学学报, 2011, 35(4): 342-326. MENG Zong, GU Haiyan. Research on fault feature extraction of rotating machine based on empirical mode decomposition and AR model[J]. Journal of Yanshan University, 2011, 35(4): 342-326. [11] 陈冬青, 许红波, 王新华. 基于ARMA模型关联维数与LSSVM的轴承损伤评定[J]. 起重运输机械, 2015(5): 51-55. CHEN Dongqing, XU Hongbo, WANG Xinhua. Bearing damage assessment based on the correlation dimension of ARMA model and LSSVM[J]. Hoisting and Conveying Machinery, 2015(5): 51-55. [12] TANG H, LIAO Y H, CAO J Y,et al. Fault diagnosis approach based on Volterra model[J]. Mechanical System and Signal Processing, 2010,24(4): 1099-1113. [13] 裘焱, 吴亚峰, 李野. 应用EMD分解下的Volterra模型提取机械故障特征[J]. 振动与冲击, 2010, 29(6): 59-61. QIU Yan, WU Yafeng, LI Ye. Applying EMD decomposition of the Volterra model to extract mechanical fault feature[J]. Journal of Vibration and Shock, 2010, 29(6): 59-61. [14] KONSTANTIN D, DOMINIQUE Z. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. [15] SALIM L. Comparative study of signal denoising by wavelet threshold in empirical and variational mode decomposition domains[J]. Healthcare Technology Letters, 2014,1 (3): 104-109. [16] WANG Yanxue, RICHARD M, XIANG Jiawei, et al. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system[J]. Mechanical Systems and Signal Processing, 2015, 60/61: 243-251. [17] ANEESH C, SACHIN K, HISHAM P M, et al. Performance comparison of variational mode decomposition over empirical wavelet transform for the classification of power quality disturbances using support vector machine[J]. Procedia Computer Science, 2015, 46: 372-380. [18] 韩敏. 混沌时间序列预测理论与方法[M]. 北京:中国水利水电出版社, 2007. [19] CHOW T W S, TAN H Z. HOS-based nonparametric and parametric methodologies for machine fault detection[J]. IEEE Transactions on Industrial Electronics, 2000, 47(5): 1051-1059. [20] PENG H C, LONG F H, CHRIS D. Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(8): 1226-1238.


2 基于相空间重构的Volterra预测模型
2.1 相空间重构
2.2 时间序列的Volterra预测模型
3 结合VMD和Volterra预测模型的特征取方法
4 滚动轴承振动信号分析
4.1 实验数据描述
4.2 轴承振动信号的VMD分解








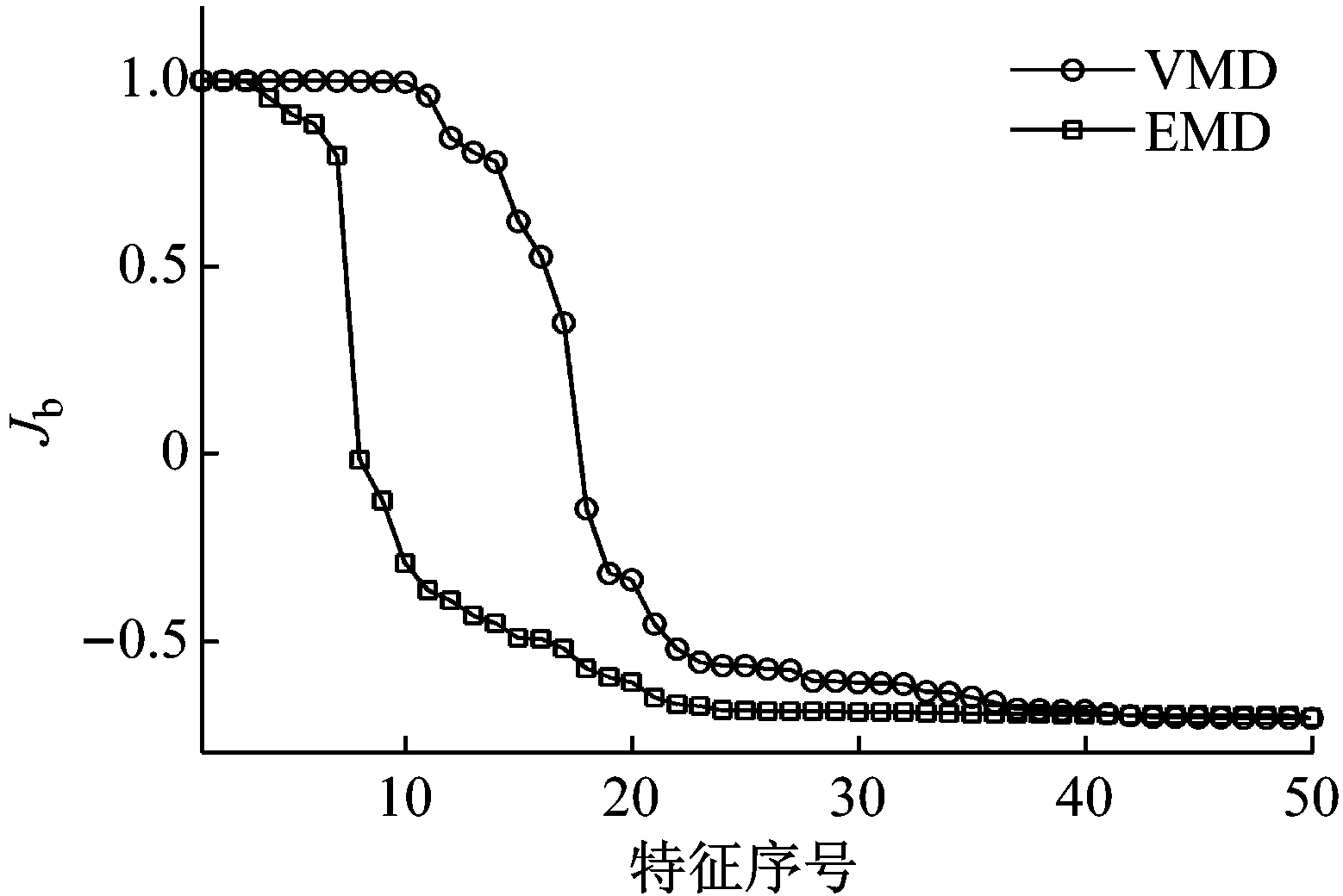
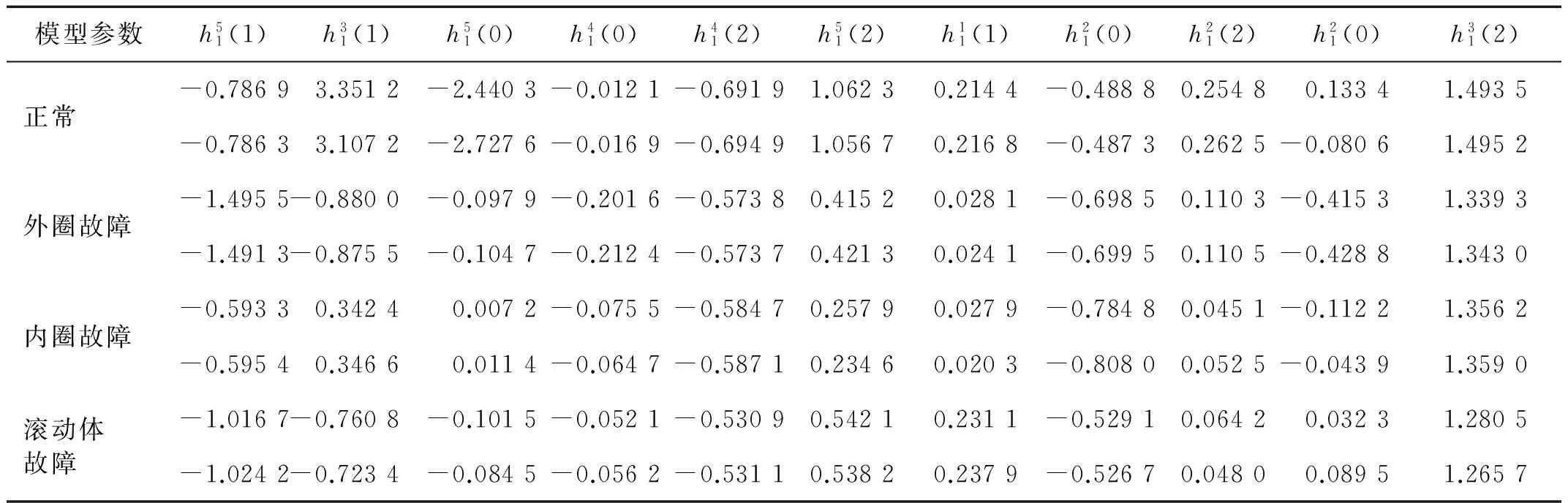
4.3 Volterra模型特征提取







4.4 轴承故障诊断效果
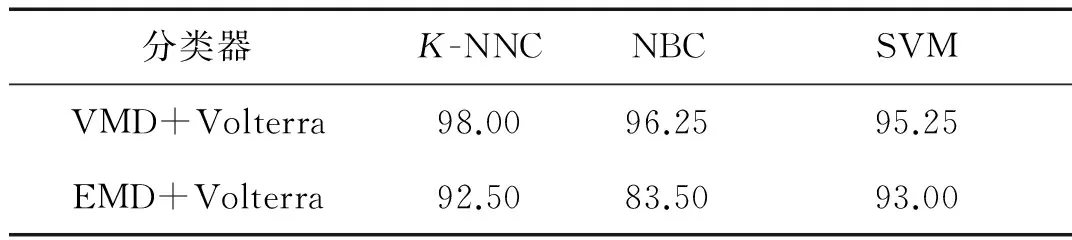
5 结 论
