气象观测数据不足的沿海地区基本风压取值方法研究＊——以台州市为例

姜喜庆 ，李瑞鸽 ＊，李 骞 ，祝东红 ，陈小素 ，付 鹏 ，沈明杰

（1.台州学院 建筑工程学院，浙江 台州 318000；2.台州市建设工程设计审查中心，浙江 台州 318000；3.台州市精筑建设工程施工图审查中心，浙江 台州 318000；4.台州市气象局，浙江 台州 318000）

0 引言

在台风频发的浙东南沿海地区，风荷载是建筑结构设计时要考虑的主要水平荷载，因此基本风压的取值是关系到结构安全性和经济性的重要参数。但是由于观测时间较长的国家基准站和基本站设置数量有限，各区域详细基本风压数据严重匮乏。以浙江省台州市为例，该市紧邻海边，并且有海岛、半岛，多山地、丘陵，地势复杂，风压变化幅度大，但是在现行的《建筑结构荷载规范》（GB50009-2012）（以下简称“现行《规范》”）中，台州市有明确取值规定的仅有四个点［1］，分别为临海市括苍山、椒江区洪家、椒江区下大陈、玉环市坎门街道（见表1所示）。除洪家外，其他三个气象站点均设置在海岛、半岛或者海拔1000多米的山顶，基本风压数据对台州市的大多数建筑结构设计没有参考意义。因此工程人员在取用各县市区的风荷载时只能参考荷载规范中全国基本风压分布图（如图1所示）的数值，按照图中等值线的标注，目测当地的位置并估算对应的基本风压。从图1中可以看出，台州市紧邻海边，风压等值线很密，风压梯度变化大，靠目测和估计很难精确取值，这也造成很多设计单位在对同一片区域的工程结构进行设计时，风压取值不同，给行政管理部门和图审机构的工作带来很大困扰。据调查，台州市各县市区的工程在进行结构设计时基本风压取值从0.45-1.45 kN/m2不等，并且没有明确统一的标准，严重影响了对工程结构安全性和经济性的控制。

图1 《建筑结构荷载规范》（GB50009-2012）风压分布图局部（台州）Fig.1 Wind pressure distribution map（Taizhou）in Load Code for the Design of Building Structures GB50009-2012

随着科技的发展，近些年来台州地区设置了大量的自动气象观测站点，安装了相当密集的自动记录式风速仪，采集到了一批可观的数据，为精确的统计和计算基本风压提供了宝贵的资料。但是由于记录时间较短，近十年来在台州正面登陆的台风几乎没有，因此建站历史较短的气象站点采用实际观测风速资料计算，得到的50年一遇最大风速值偏小，不能直接作为建筑结构设计依据。所以研究气象观测数据不足的沿海地区基本风压取值方法是迫在眉睫的工作。

1 基于现行《规范》规定方法的基本风压取值计算

1.1 计算方法

国内外学者对年风速最大值的概率分布研究主要集中在极值I型分布、威布尔分布和P-III型分布模型［2，3］。纪鹏远等人根据澳门地区风速数据对极值I型分布、威布尔分布和P-III型分布模型进行了拟合检验，结果表明极值I型概率分布的拟合效果最好［4］，而且极值I型分布是目前极值概率分布计算最常用的模型［5，6］，美国的规范和我国现行《规范》也采用了该模型［7］。根据我国现行《规范》规定：风速数据资料积累年限一般应在25年以上，最低不宜少于10年，且观测数据应考虑均一性。风速按年最大值取样，采用极值I型概率分布模型，计算50年一遇10 m高10 min平均最大风速，得到重现期50年的基本风速。基本风速与风压的关系如下：

由于实际设置的气象站超过25年观测历史的很少，所以，采用不低于10年期的站点资料。

根据极值I型概率分布模型［1］，风速的分布函数为：

拟求50年一遇的风速，即x＜xmax的概率为49/50，则：

两边取两次自然对数并化简得：

其中u和α分别是对应极值I型概率分布的位置参数和尺度参数，可根据采集到的历年风速最大值的平均值、标准差及采集年限计算确定。

1.2 计算结果分析

按照规范规定方法，对台州市10年以上风速积累数据的84个站点进行分析计算，发现一部分站点的基本风压计算值很不合理，在表1中仅列出其中一部分站点计算值。

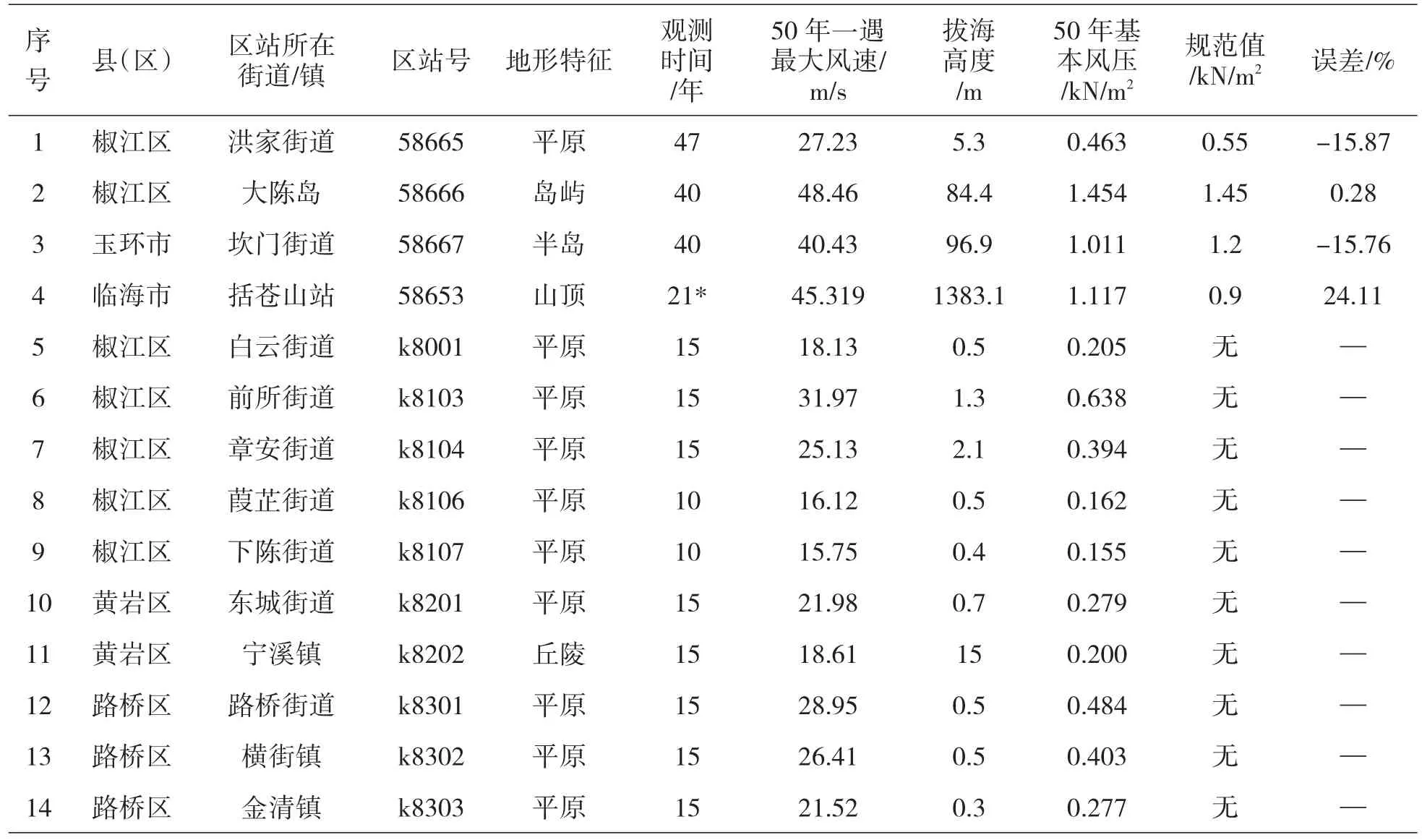
表1 台州市部分站点按照规范计算的基本风压值Table．1 Local basic wind pressure values calculated according to the codes in Taizhou.

由表1可知，数据采集时间超过30年的站点，基本风压计算值与规范取值比较接近，58665（以下简称“洪家站”）和58667两个站点计算值比规范取值小15%左右；58666站点计算值与规范值基本不存在偏差；58653站点计算值比规范取值大24.11%。这些站点的基本风压与现行《规范》给出的风压等值线相比较，也具有一致性；但是对于观测时间较短的站点，基本风压计算值明显不合理。例如编号为k8103、k8104、k8106、k8107的站点对应的位置在洪家街道附近，并且地貌均为平原，在风压等值线图上，应该处于大小相等的位置，但是根据历年最大风速的统计值进行计算，却得到了最大0.638 kN/m2，最小0.155 kN/m2的基本风压值，最大值和最小值相差超过4倍，显然不合理。

1.3 存在问题及原因分析

根据气象站点实际采集到的历年最大风速，按照现行《规范》规定的方法进行计算，经纬度相近，地理环境同为平原的站点，基本风压计算值明显差别巨大，因此不可盲目采用该数值作为设计依据。通过分析发现，如果不考虑地理环境因素、观测数据误差等不可控制的原因，仍然还有两个方面的必然因素，导致了不合理的结果。

（1）观测年限短，观测期内未出现台风天气。序号为k8106和k8107的两个站点设置时间为2006年以后，观测年限为10年，通过调查气象资料发现，2005年以后，没有在台州登陆的台风记录，因此，采集到的历年最大风速样本值明显偏小，利用该批样本作为统计参数计算出的50年一遇最大风速值显然是不可靠的。

（2）极值I型分布的数值特征引起的误差。根据极值I型概率分布的特征和概率分布函数可知，在一定的观测年限内，如果每年的风速最大值离散性大，则计算出的50年一遇的最大风速值偏大。例如A和B两个站点，年最大风速值观测如表2所示，在10年内A站点和B站点观测到的风速最大值都为20 m/s，但是A站点历年最大值都接近20 m/s，而B站点历年最大值都比较小。直观推断，A站点附近的建筑物更应该注重抗风设计，但是按照极值I型分布计算出的50年一遇最大风速值却是B站点比A站点大75%。这个计算结果解释了当某些站点观测时间短，并且观测时间内没有出现极端天气，观测数值离散性小，则会造成50年一遇的最大风速小，基本风压计算值偏小的现象。

表2 极值I型分布风速数据离散性对50年一遇最大风速计算值的影响Table．2 Influence of the 50 years maximum wind speed by dispersion of type I extreme value wind speed data

鉴于以上两种因素的影响，在进行基本风压计算时，不能直接按照极值I型的分布函数采用历年气象观测数据进行计算，而应该对观测数据根据均一性原则进行合理的推测处理和样本选择。

2 基于国家级站点观测值的历年最大值风速推测

由于观测年限短，观测资料不足造成的基本风压计算不合理的情况，可以参考观测时间长的国家级站点的风速数据，通过数据拟合的方法进行历年最大值风速的推测和插补，计算出合理的50年一遇风速最大值，得到可以作为建筑结构设计依据的基本风压值。

2.1 风速均一性检验

在采用风速拟合推测的方法之前，必须检验站点之间风速是否符合均一性。在本例中，洪家为国家级站点，观测年限为47年，可以作为参考站点，其他站点的年风速最大值和每天风速最大值的变化都应该具有相关性和均一性，否则盲目使用拟合方程推测将会得到错误的结果。

由于年风速最大值一般出现在7、8、9三个月份当中，因此需检验2004-2017年7月、8月和9月的风速均一性。以k8103站点为例，两个站点之间每天最大值风速的相关性和均一性，如图2所示。自建站以来k8301站点的风速最大值发生在2005年9月，在图3中亦可直观看出，两个站点之间9月份日最大值风速也具有明显的均一性。

图2 k8103和洪家站2004-2017年7、8、9月日最大风速关系图Fig.2 Daily maximum wind speed relationship between k8103 and Hongjia station in July to September from 2004 to 2017

图3 2005年9月洪家和k8103日风速最大值Fig.3 Daily extreme value of wind speed in Hongjia and k8103 station in September 2005

由图可知，两个站点之间日最大风速具有明显的线性关系。

对2003-2017年之间，两个站点的年风速最大值进行研究，如表3所示。

表3 洪家基准站与k8103站点自2003年以来历年最大风速Table．3 Annual extreme wind speed of Hongjia and k8103 station since 2003

计算其相关系数：

其中cov（X，Y）为两个站点自2003年以来历年风速最大值的的协方差，DX和DY分别为洪家站点和k8103站点自2003年以来历年风速最大值的方差。

将表中数值代入计算，其相关系数达到0.9233说明具有非常强的相关性。

2.2 极值风速回归分析及拟合方程修正

以k8103站点为例进行说明。由于两个站点采集到的风速最大值具有极强相关性，因此可以对两个站点的观测数据进行拟合，并采用拟合方程推测k8103站点缺失年度的最大值风速。

采用最小二乘法进行拟合，则可得到回归方程：

用F检验对回归方程做显著性检验，检验结果见表4.

表4 回归方程的方差分析表Table．4 Variance analysis table for regression equation

由表4可以看出，回归方程的F值为75.17，远大于显著性水平为0.01的拒绝域9.074，k8103站点的历年风速最大值与洪家站点的历年风速最大值具有明显线性关系，回归方程是适合的。

考虑到大值优先及更大的可靠概率，对拟合曲线进行修正（如图4a所示的虚线），修正后的回归方程为：

采用同样的方法对其他站点最大风速数据进行均一性检验和拟合，并修正，如图4所示（图中虚线为修正后的拟合曲线）。

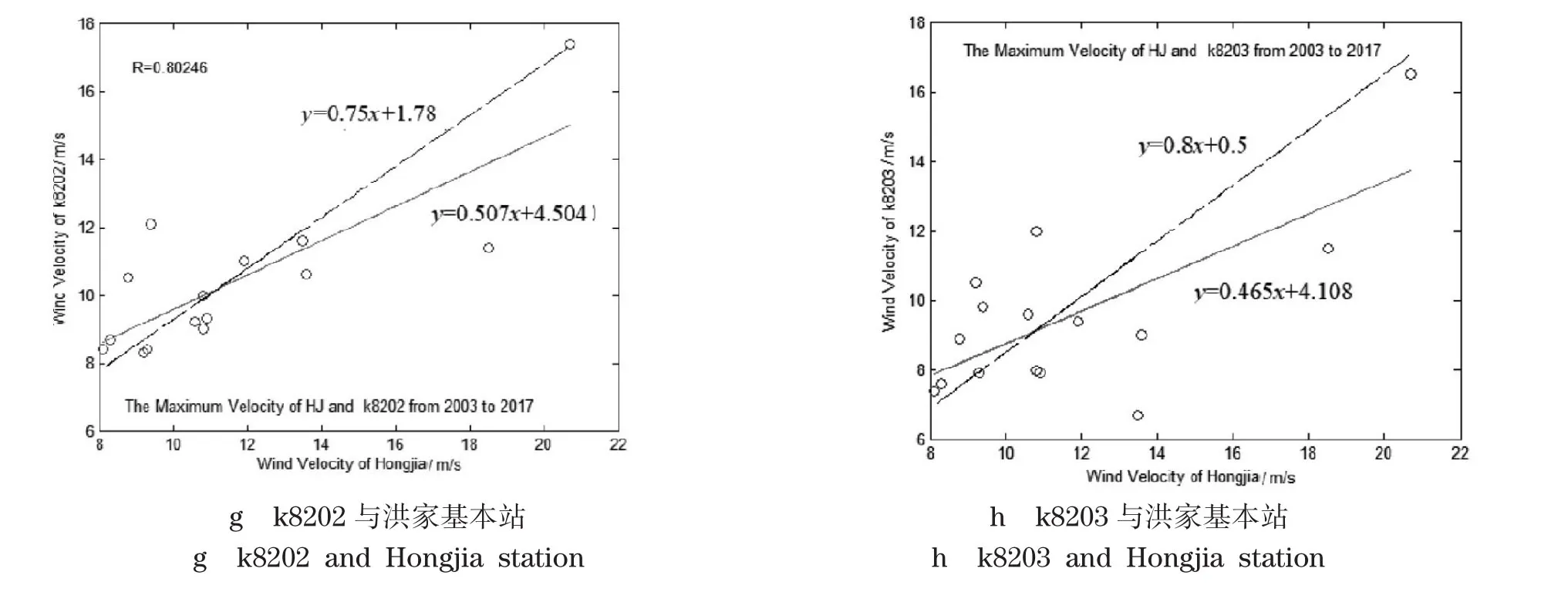
图4 地方站与洪家基本站观测值相关性图Fig．4 Correlation diagram between local station and Hongjia basic station

2.3 计算结果对比

按照最小二乘法回归分析得到公式并修正，得到方程（7），采用（7）式拟合k8103历年风速最大值，并与洪家基准站观测到的年风速最大值进行比较，如图5所示。由图5可以看出，2003年前后期风速最大值变化符合均一性原则。

图5 回归方程拟合的k8103历年风速最大值Fig.5 Wind speed maximum value fitted by regression equation of k8103 station

采用修正后的公式进行计算，得到的50年一遇最大风速值和基本风压值见表5。本文计算洪家站点的基本风压值与现行《规范》值相比略小，原因是近10年来台州未正面遭遇台风登陆。而现行《规范》中基本风压计算所采用的资料为2008年之前的风速数据。

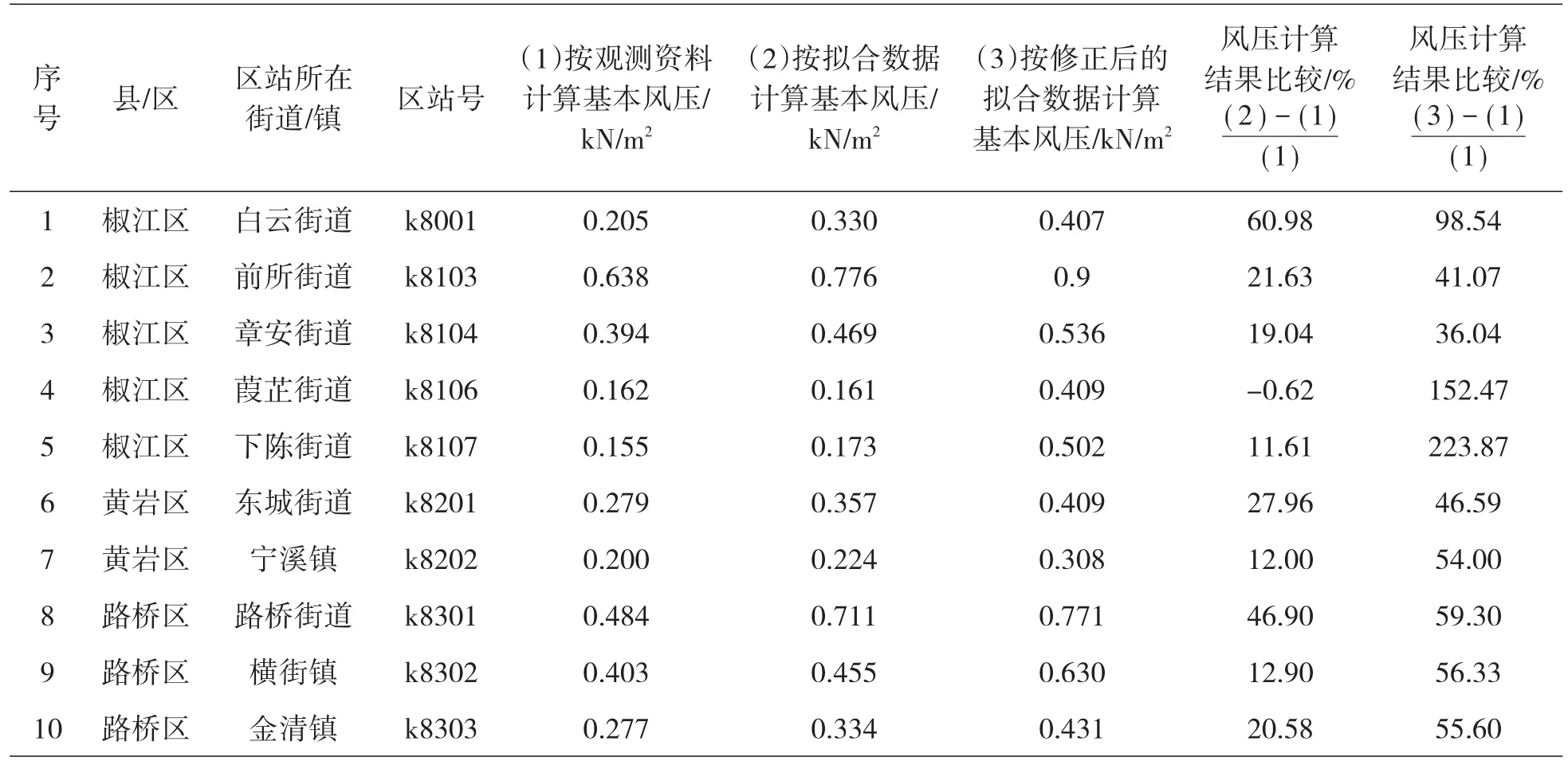
表5 基本风压计算值对比Table．5 Comparison of wind pressure basic values

3 结论

对于建站历史短的气象站，本文根据实际采集到的短期历年风速数据，对比建站历史长的国家级站点风速数据，采用回归分析的方法，插补了新建站点长期的历年风速最大值，计算基本风压并进行了对比。并得到以下结论：

（1）建站历史较短的气象站计算基本风压时，不能直接采用实际采集到的风速数据，由于台风登陆的随机性，观测年份短的站点采集到的台风信息少甚至缺失，造成基本风压取值过小，以此为依据进行结构计算则会影响结构安全性。

（2）采用回归分析的方法拟合历史短的站点与参考站点的关系推出长期风速数据，进而计算该站点所在地的基本风压是可行的，前提条件是两个站点之间必须有足够强的相关性。

（3）采用最小二乘法得到的拟合公式是基于误差平方和最小的原则，在计算50年一遇风速最大值时，观测值中较大的风速贡献率更高，因此应该对拟合公式进行调整，优先考虑大值的拟合度。

（4）由于浙东南沿海地区多山地丘陵和岛屿，地势复杂，有些站点的观测数据与国家站或者观测历史久远的基准站观测数据之间都不存在明显的相关性，则需要通过其他方法进行分析，例如数值仿真、风洞试验等方法。