感知器神经网络线性可分判断的满足性算法＊

赵威亦，陈相锦，董怡雯，周冰滢，王 杰，贺勤斌＊

（1.台州学院 航空工程学院，浙江 台州 318000；2.台州学院 电子与信息工程学院，浙江 临海 317000；3.台州学院 商学院，浙江 台州 318000）

0 引言

人工智能目前在机器人、经济政治决策、控制系统以及仿真系统中得到广泛应用.目前能够用来研究人工智能的主要物质手段以及能够实现人工智能技术的机器就是计算机.人工智能的发展历史是和计算机科学与技术的发展史联系在一起的.除了计算机科学以外，人工智能还涉及信息论、控制论、自动化、仿生学、生物学、心理学、数理逻辑、语言学、医学和哲学等多门学科.随着大量数据计算处理，计算机的计算速度成为计算瓶颈.目前人们对计算机速度处理，往往是采用多核处理器、大型计算机处理.但是人工智能的小型化发展是必然的趋势，因此新的硬件设计和研究越来越重要.美国学者F.Rosenblatt提出的感知器网络（Perceptron networks）是人工神经网络的重要组成部分，它具有人类大脑的自组织、自学习的功能，其应用非常广泛，涉及电子科学与技术、信息科学、通信工程、计算机科学与技术、控制科学与技术等领域［1-4］.感知器神经网络成为了一个新的研究方向.感知器神经网络的线性可分判断是感知器领域一个重要的研究内容［5］.

满足性问题是多个不同学科的交叉问题，它是一类著名的NP-完全问题［6，7］.最优可满足性问题是一个重要的研究对象，国际上的研究十分活跃，这类典型的NP完全问题大量地出现在军事系统、通讯网络、计算机集成系统中［7］.在算法设计与分析的研究中，最优可满足性问题是一个重要而又困难的研究对象.但是，随着满足性判定算法性能的不断提升，它已经被大量的应用于实际问题的求解，例如计算机优化算法、系统生物学、运筹学和管理科学领域.

本文对满足性问题进行研究，把满足性算法应用于感知器神经网络的线性可分判断，我们希望取得较好的计算效果.

2 相关概念及算法

2.1 布尔函数

定义1：布尔函数可以由下列映射表示:

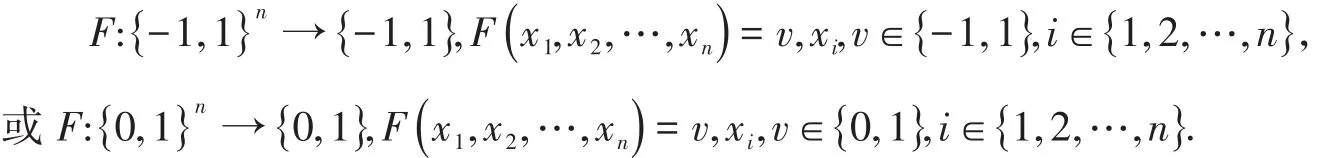
显然，一个n输入布尔函数可以由一个n维立方体表示.图1给出两个2输入布尔函数的2维立方体表示.

图1 两个2输入布尔函数的2维立方体表示

表1 n输入布尔函数的输入窗口表示

2.2 线性可分布尔函数

定义 2［8］：n 输入的 Boolean 函数称为线性可分的（Linearly separable），如果存在向量W=(w1,w2,…,wn)和阈值 θ，使得

几何上看，一个n输入布尔函数线性可分当且仅当存在一个n-1维超平面w1x1+w2x2+…+wnxn-θ=0，它将 n维超立方体的-1顶点与+1顶点分离两个部份 .自然，图 1（a）函数是线性可分的，图1（b）函数是非线性可分的.

任一个非线性可分布尔函数可以由线性可分布尔函数通过“异或”（XOR）得到［9，10］.而线性可分布尔函数在硬件电路上实现比较容易.但是，依照定义判断一个布尔函数是否线性可分非常困难.因此，对于任意一个布尔函数的线性可分判断变得重要.

定义 3［11］：记的极小子系统，如果满足i0+i3=i1+i2和σi0+ σi3=σi1+σi2.当极小子系统是线性可分的，则称为相容极小子系统，否则称为不相容极小子系统.

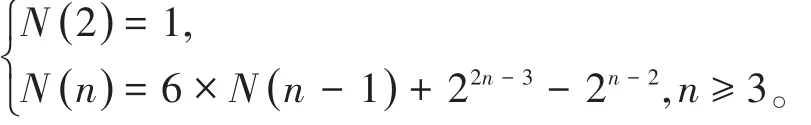
引理1［11］n输入布尔函数的极小子系统的个数为：例如，当n=3时，若给定某一函数则该函数有12个极小子系统，分别为

引理2［11］n输入布尔函数线性可分当且仅当其N(n)个极小子系统都是相容的，即任一极小子系统满足

则引理1和引理2容易得到下列结果：

推论1 n输入布尔函数的所有可能不相容极小子系统个数为2N(n).

在不引起混淆情况下，本文的二值输入输出变量{- 1,1}可以用{0 ,1}或{F ,T}表示.基本逻辑运算有逻辑与(∧)、逻辑并(∨)、逻辑非(～)、蕴含(→ )以及等价(↔ 或=)等.

定 义 4［12］：逻 辑 式，称 逻 辑 式 φ 为 析 取 范 式 .这 里是子句，li1∈{0 ,1}为文字.

在逻辑式析取范式φ中当某一子句为“真”，则φ为“真”，即φ=T.

定 义 5［12］：逻 辑 式称 逻 辑 式 φ 为 合 取 范 式 .这 里

在逻辑式合取范式φ中当某一子句为“假”，则φ为“假”，即φ=F.

定理 1［12］若 f，p是逻辑式，则

显然，逻辑蕴含满足分配律、结合律.

推论2 若f，p(i=1,2,…,k)是逻辑式，则

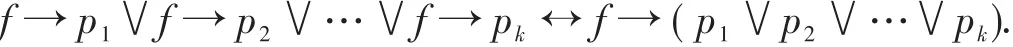
定理2 单元消解：若p为文字，A为逻辑式，则满足

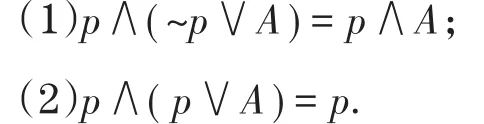
证明：我们通过计算真值表，

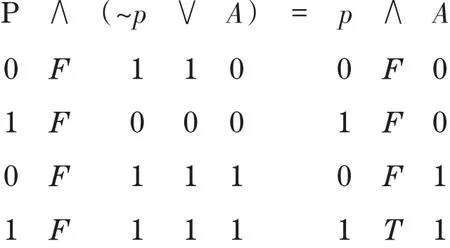
另外，

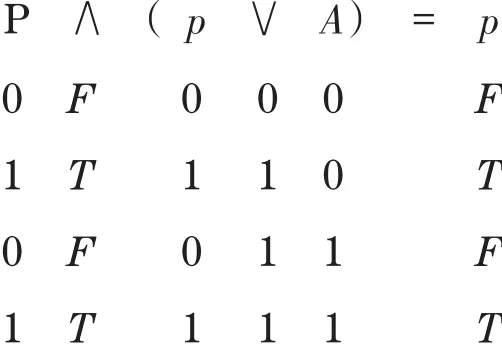
显然，所证成立.

定理3 记p为n输入布尔函数的一个极小不相容子系统，对于任意一个布尔函数f，若存在p满足f∧～p=F，则布尔函数f非线性可分，否则布尔函数f线性可分.

证明：由p为n输入布尔函数的一个极小不相容子系统；若f→p=T，即～(f→p)=F，则布尔函数f至少含有一个极小不相容子系统.由定理1上式即，～(f→p)=～(～f∨p)=F.另外，由引理1和引理2知，布尔函数f非线性可分；自然，若f∧～p=T即布尔函数f线性可分.证毕.

定理4 记pi(i=1,2,3,…,2N(n))为n输入布尔函数的极小不相容子系统，对于任意一个布尔函布尔函数f非线性可分，否则布尔函数f线性可分.

证明：由推论2、定理3和摩尔定律显然成立.

由定理2和定理3，

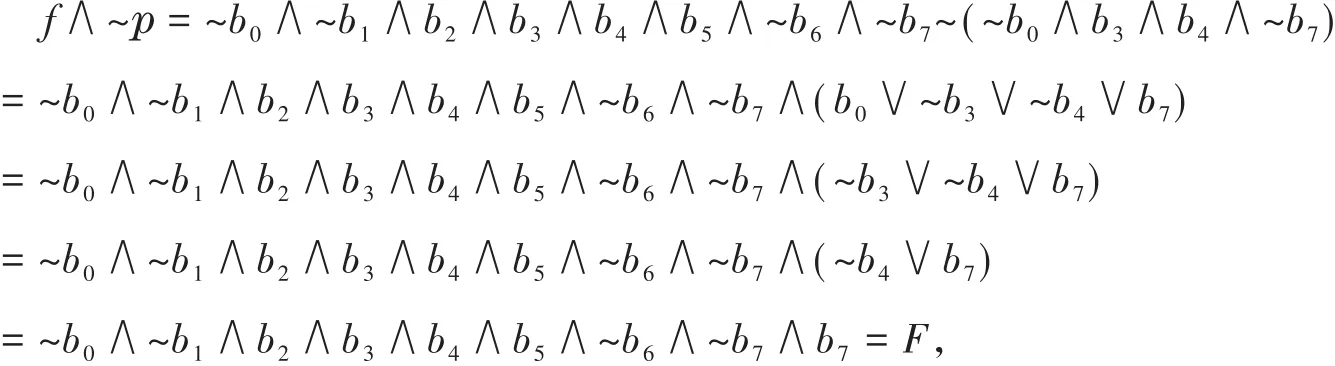
即f为3输入非线性可分布尔函数.

逻辑满足性算法与判断应用非常广泛，现今有大量的研究文献，人们也提出各种各样的算法.在许多工具软件，比如R语言、python语言、matlab等都有满足性求解器或相应的支持包文件.实际上对任意一个布尔函数的线性可分性判断我们可以通过现有满足性求解器来判断.

由引理1易知3输入布尔函数有如下24个极小不相容子系统：

对于例1，我们也可以利用定理4和matlab满足性求解器来计算.对于合取范式matlab满足性求解器，我们得到即f为3输入非线性可分布尔函数.

3 结论

判断一个n输入布尔函数f线性可分性问题，通常只要遍历其可能的所有极小子系统，当存在其某一极小子系统为不相容的，则该布尔函数f是非线性可分的，否则该布尔函数f是线性可分的.本文提出利用逻辑满足性算法判断布尔函数的线性可分性.虽然，我们利用逻辑满足性算法在判断函数线性可分性的速度上并没有提高.但是，我们给出了n输入布尔函数f线性可分性判断的一个新的方法.另外，满足性算法也有可能应用于n输入布尔函数f的线性分解以及实施，这也为我们以后的进一步研究提供了思路和方向.