函数观点看数列

徐建东

高中教材必修5（苏教版）中的数列定义是：数列可以看成以正整数集N*（或它的有限子集｛1，2，3，…，k｝）为定义域的函数an＝f（n），当自变量按照从小到大的顺序依次取值时，所对应的一列函数值.

由此我们知道，数列可视为特殊的函数，可以用函数的观点来看待数列，用研究函数的方法来研究数列.这为我们提供了一个更高的观点.当然，同时要注意数列的特殊性：其定义域是正整数集或其有限子集｛1，2，3，…，k｝.因此在数列的图象、最值、单调性、周期性等方面有其特殊的表现形式，如果不加注意也会产生错误.

一、函数视角下的数列的图象和最值

例1求数列前n项和Sn＝n2-3n＋1的最小值.

分析考虑到数列前n项和Sn＝n2-3n＋1是关于n的二次函数，所以我们可以构造函数f（x）＝x2-3x＋1，通过对函数图象的研究来得到数列前n项和Sn＝n2-3n＋1的最值，我们可以列表如下：

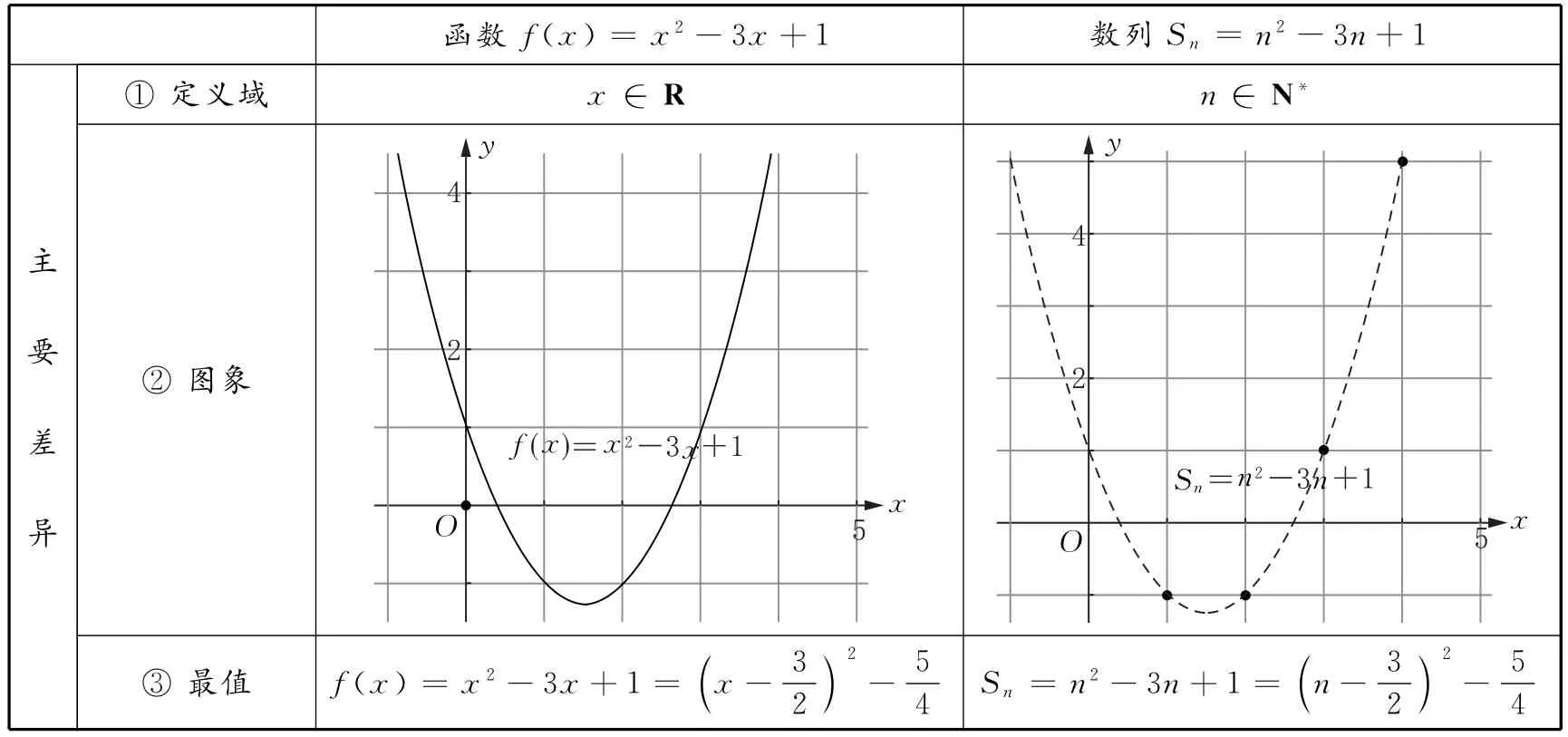
函数f（x）＝x2-3x＋1 数列Sn＝n2-3n＋1主要差异①定义域 x∈R n∈N*②图象③ 最值 f（x）＝x2-3x＋1＝ x-32（ ）2-54 Sn＝n2-3n＋1＝ n-32（）2-54

由此我们看到数列中的如下结论：因两者在定义域上的显著差异，导致其在图象和最值上的差异，主要为：函数f（x）＝x2-3x＋1的图象是一根开口向上的光滑的抛物线，而数列Sn＝n2-3n＋1的图象是抛物线上的一系列离散的点.函数在时取得最小值而数列在n取1或者2时才会取得最小值-1.

二、函数视角下的数列的单调性

例2已知｛an｝是递增数列，且对任意的n∈N*，都有an＝n2-λn恒成立，求实数λ的取值范围.

错解设函数f（x）＝x2-λx，

因为｛an｝是递增数列，所以f（x）＝x2-λx在[1，＋∞）上是单调递增函数，

正解1因为数列｛an｝是单调递增数列，所以an＜an＋1对n∈N*恒成立，

即n2-λn＜（n＋1）2-λ（n＋1）对n∈N*恒成立；

所以λ＜2n＋1对n∈N*恒成立，所以λ＜3.

正解2设函数f（x）＝x2-λx，因为｛an｝是递增数列，结合f（x）＝x2-λx的图象，可知对称轴解得λ＜3.

函数单调性的定义中，所取的两个自变量是定义域A的子区间I上的任意两个量，而数列单调性中，自变量取的是相邻的两个正整数.在求最大和最小值时，数列中的n只能在整数内取值.如果结合图象，我们可以把这些看得更清楚.

三、函数视角下的数列的周期性

例3已知数列｛an｝中，a1＝1，a2＝2，且有an＋2＝an＋1-an（n∈N*），求S2017.

分析对于这个数列，我们很难求出其通项公式，我们能做的也只能是尝试着写出数列的前几项，试着找找有没有规律，我们发现：

至此，我们已发现，这个数列是一个以6为周期的周期数列，要求数列的前2017项的和，每个周期内6项的和等于0，S2017＝1.

结语：

学习数列，不能离开函数思想方法的指导，因为数列是特殊的函数；但在数列的学习中，也不能将自变量离散变化的数列完全等同于自变量连续变化的函数，毕竟数列是特殊的函数.