某商用车排气系统吊钩结构与位置优化分析
2018-02-25袁守利张顺风
袁守利,张顺风
(1.武汉理工大学 现代汽车零部件技术湖北省重点试验室,湖北 武汉 430070;2.武汉理工大学 汽车零部件技术湖北省协同创新中心,湖北 武汉 430070)
汽车排气系统的噪声、振动、声振粗糙度性能是整车NVH 性能的重要组成部分,在整车性能中有着重要意义[1]。排气系统振动的激励源主要有发动机的机械振动、发动机的气流冲击、声波激励和车身振动。由于发动机与排气系统直接连接,因此发动机的振动将会直接传递给排气系统,不但会引起排气系统自身的振动,而且还会通过排气系统吊钩将振动传递给车身,进而直接影响整车的噪声与振动水平[2-3]。因此,在整车开发设计时对排气系统的模态、振动、强度分析、吊钩位置的优化是汽车设计中必不可少的环节,同时也是缩短研发周期,降低研发成本的重要途径[4]。
笔者以某车企商用车为例,对该车排气系统进行有限元分析,并通过自由模态试验验证了所建有限元模型的合理性,为排气系统静力学、动力学、传递力及位移响应的分析计算以及计算结果的正确性提供了。在对排气系统吊钩进行优化分析时,采用单个吊钩约束模态进行分析,将分析结果与企业所给吊钩约束模态目标值进行对比,并对不满足企业要求的吊钩进行结构优化处理,优化后吊钩约束模态满足企业要求。最后,利用平均驱动自由度法(ADDOFD)计算出吊钩最佳悬挂点位置,并进行了吊钩位置的优化处理。
1 排气系统有限元模型的建立
首先,根据车企提供的商用车排气系统尺寸标准,利用CATIA三维建模软件建立排气系统几何模型,将建好的几何模型导入到有限元软件Hypermesh中进行几何简化处理与网格划分。
该排气系统由法兰盘、波纹管、排气管道、隔热罩、三元催化器、排气吊钩与吊耳、前消声器、后消声器组成。由于该排气系统除法兰盘、排气吊钩以外,各个组件的壁厚都较薄,且与其长度差值较大,因此在理论上可以将其各个组件视作薄壁板壳结构,可采用Shell单元进行模拟;用Solid单元模拟法兰盘和排气吊钩;用弹簧阻尼单元CBUSH模拟波纹管与橡胶吊耳。整个排气系统用 rbe2刚性单元、rbe3点焊单元和weld面单元单元连接。排气系统使用的材料属性如表1、表2所示。排气系统有限元模型及吊钩位置如图1所示。

表1 材料属性表
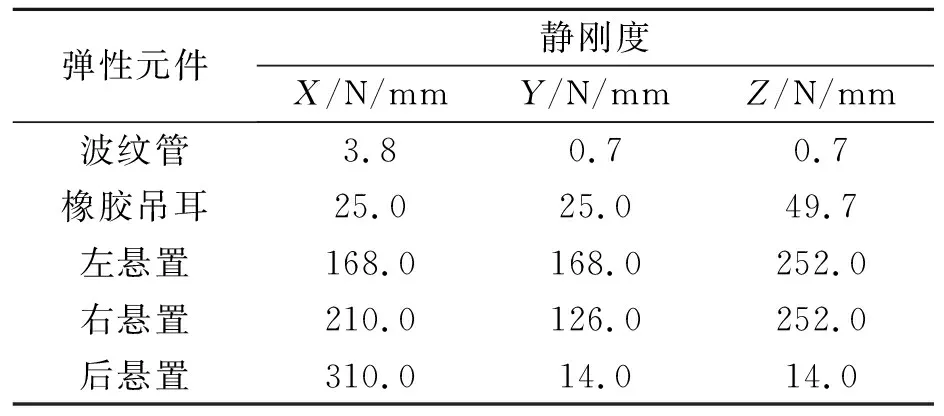
表2 弹性元件刚度参数

图1 排气系统有限元模型
2 排气系统模态分析与试验验证
2.1 排气系统自由模态分析
模态是机械结构的固有振动特性,每一个模态具有特定的固有频率和模态振型。排气系统动力计算的关键就是要对有限元模型进行模态分析。而模态分析的目的是为了识别系统的模态参数,为后续系统的振动特性分析、振动故障诊断和预报、结构动力学特性优化设计提供依据。由于排气系统与发动机和车身直接相连,因此排气系统的模态必须与发动机激励频率的模态分开,否则会产生系统耦合,引起强烈的共振[5]。
根据发动机激励频率计算公式:
(1)
式中:k为汽缸数;n为转速;T为冲程数。
企业提供的发动机参数为:四缸四冲程汽油发动机;最高转速为6 000 r/min。根据以上数据可计算出发动机的最高激励频率为200 Hz,故排气系统在进行模态分析时只需要分析200 Hz以内的模态即可。
然后利用有限元软件Hyperwoks中的OptiStruct求解器模块,对排气系统有限元模型进行自由模态分析。提取前16阶固有模态频率和振型,其中1 ~ 6阶为刚体模态,7 ~ 16阶为计算分析模态。由此可得排气系统自由模态的各阶频率数据如表3所示。
从表3可知,其前6阶固有频率较小,为刚性模态。因为在该模态下,排气系统作为一个刚体整体振动。由第7 ~ 16阶的模态振型图可知,对应于不同振动模态来说,与发动机直接相连的排气系统前端垂向弯曲、横向弯曲振动位移较大,如图2和图4所示。与法兰盘连接处的排气管道垂向弯曲、横向弯曲振动位移较大,如图3和图5所示。

表3 排气系统自由模态各阶频率
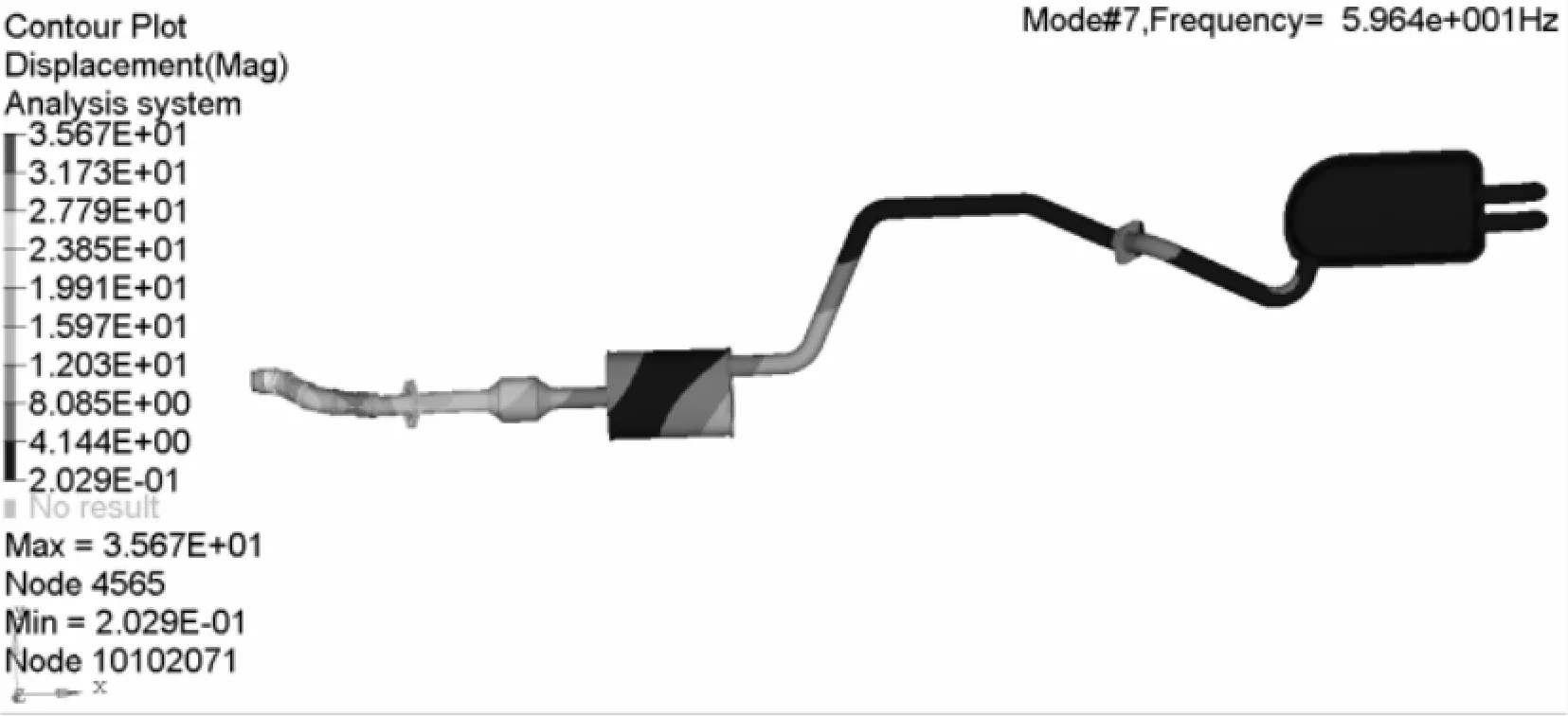
图2 第7阶振型

图3 第8阶振型

图4 第11阶振型

图5 第16阶振型
2.2 自由模态试验及模型验证
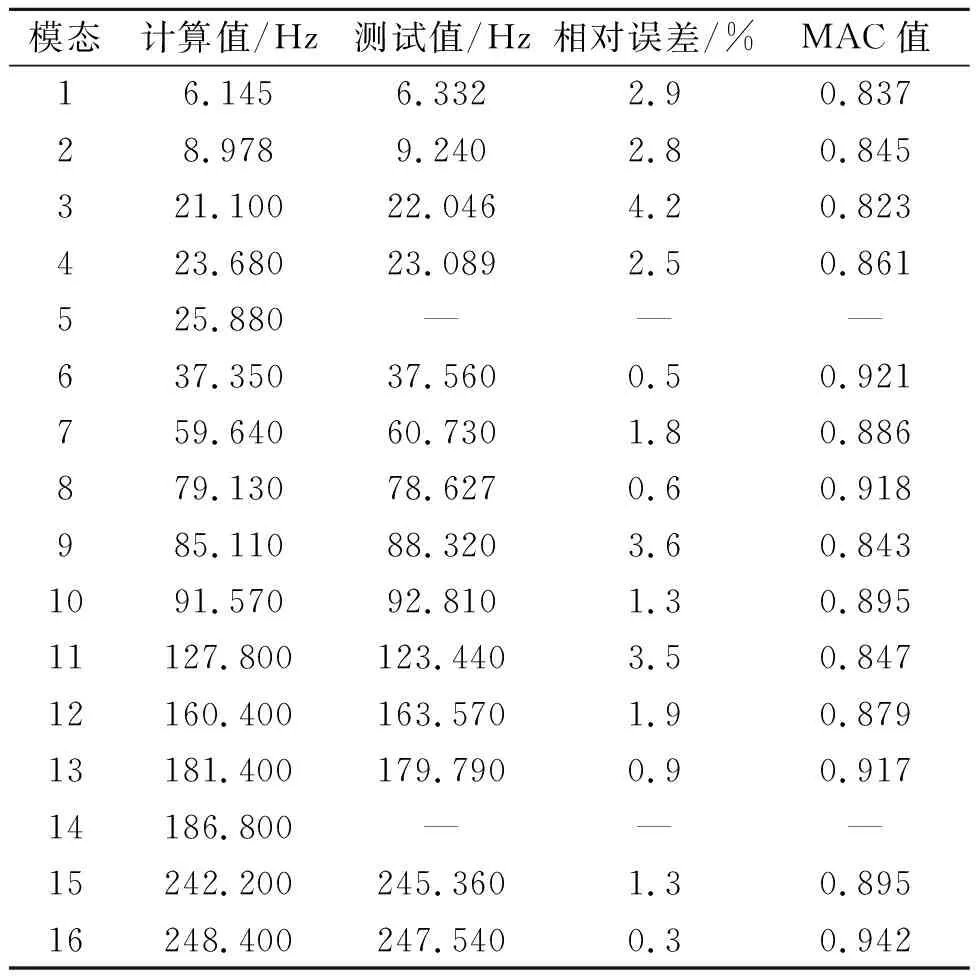
为了确保有限元仿真模型的准确性和分析结果的可靠性,需对排气系统进行自由模态试验,来验证有限元模型的合理性。在进行模态试验时,尽量使用对排气系统自由状态影响较小且不易断裂的细软绳将其进行悬置,以减少试验误差。在排气系统的排气管上选择恰当的位置布置加速度传感器,检查接线与加速度传感器是否牢固,用人工力锤锤击排气系统以产生激励,各点振动加速度信号用软件LMS Test Lab数据采集系统记录,为减小随机误差,每一个测试点需测量三次。自由模态试验现场如图6所示。用模态置信准则MAC(modal asurance criterion)值检验试验振型和有限元分析振型的一致性[6]。将有限元仿真结果、测试试验结果、二者模态相对误差以及模态振型的MAC值进行对比分析,如表4所示。

图6 自由模态试验现场
模态计算值/Hz测试值/Hz相对误差/%MAC值16.1456.3322.90.83728.9789.2402.80.845321.10022.0464.20.823423.68023.0892.50.861525.880———637.35037.5600.50.921759.64060.7301.80.886879.13078.6270.60.918985.11088.3203.60.8431091.57092.8101.30.89511127.800123.4403.50.84712160.400163.5701.90.87913181.400179.7900.90.91714186.800———15242.200245.3601.30.89516248.400247.5400.30.942
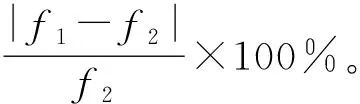
3 排气系统振动分析
3.1 排气系统静力学分析
为了分析对比各橡胶吊耳预载荷分布均匀情况,判断吊钩位置设计的合理性;验证排气系统是否满足静力学分析的设计要求,对排气系统进行1 g静力学分析[7-8]。根据企业设计要求,在对排气系统施加1 g重力加速度进行静力学分析时,系统最大位移不得超过5 mm,橡胶吊耳预载荷不超过50 N,分析结果如表5所示。由表5可知,系统的最大位移为4.48 mm,橡胶吊耳最大受力为41.18 N,均满足设计要求。
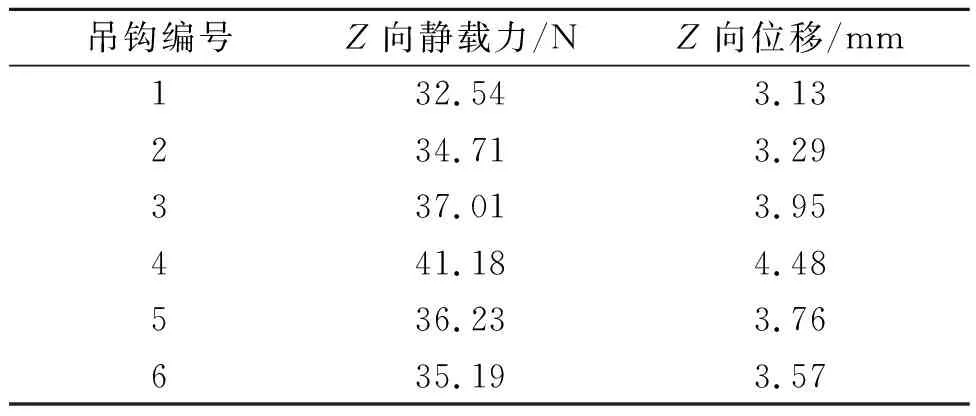
表5 1 g静力学分析结果
3.2 排气系统动力学分析
对排气系统进行动力学分析,主要是为了考察其受到随时间变化的力载荷及其对阻尼和惯性的影响。排气系统动力学分析的一个重要目的是分析其传递到车身上的力及响应。对于一般乘用车而言,传递到车身的力一般应小于10 N,而当这个力大于这个值时,在车内可能会导致一定的结构噪声[9]。
图7为排气系统振动分析时含动力总成的有限元模型。在进行排气系统振动分析时,动力总成是不可或缺的一部分,因为有无动力总成会直接影响排气系统约束模态的模态频率。

图7 排气系统传递力分析有限元模型
3.2.1 排气系统传递力分析
对排气系统进行传递力分析,其目的是分析排气系统振动传递到车体上力的大小,从而验证设计的合理性,一般车型小于10 N即可。吊钩传递力响应曲线如图8所示,6个吊钩传递力均小于2 N,均满足设计要求。
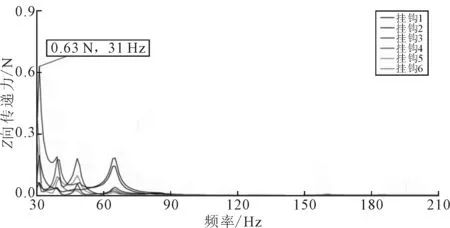
图8 吊钩传递力响应曲线
3.2.2 排气系统位移响应分析
排气系统位移响应分析目的是为了分析排气系统吊钩响应位移的大小,一般车型应小于0.5 mm。如图9所示,6个挂钩的响应位移均小于0.01 mm,故均满足设计要求。

图9 吊钩位移响应曲线
3.2.3 排气系统应力分析
模态分析结果表明:在最大扭矩250 N·m的扭矩作用下,排气系统最大应力为0.95 MPa(31 Hz),如图10所示,满足强度要求。
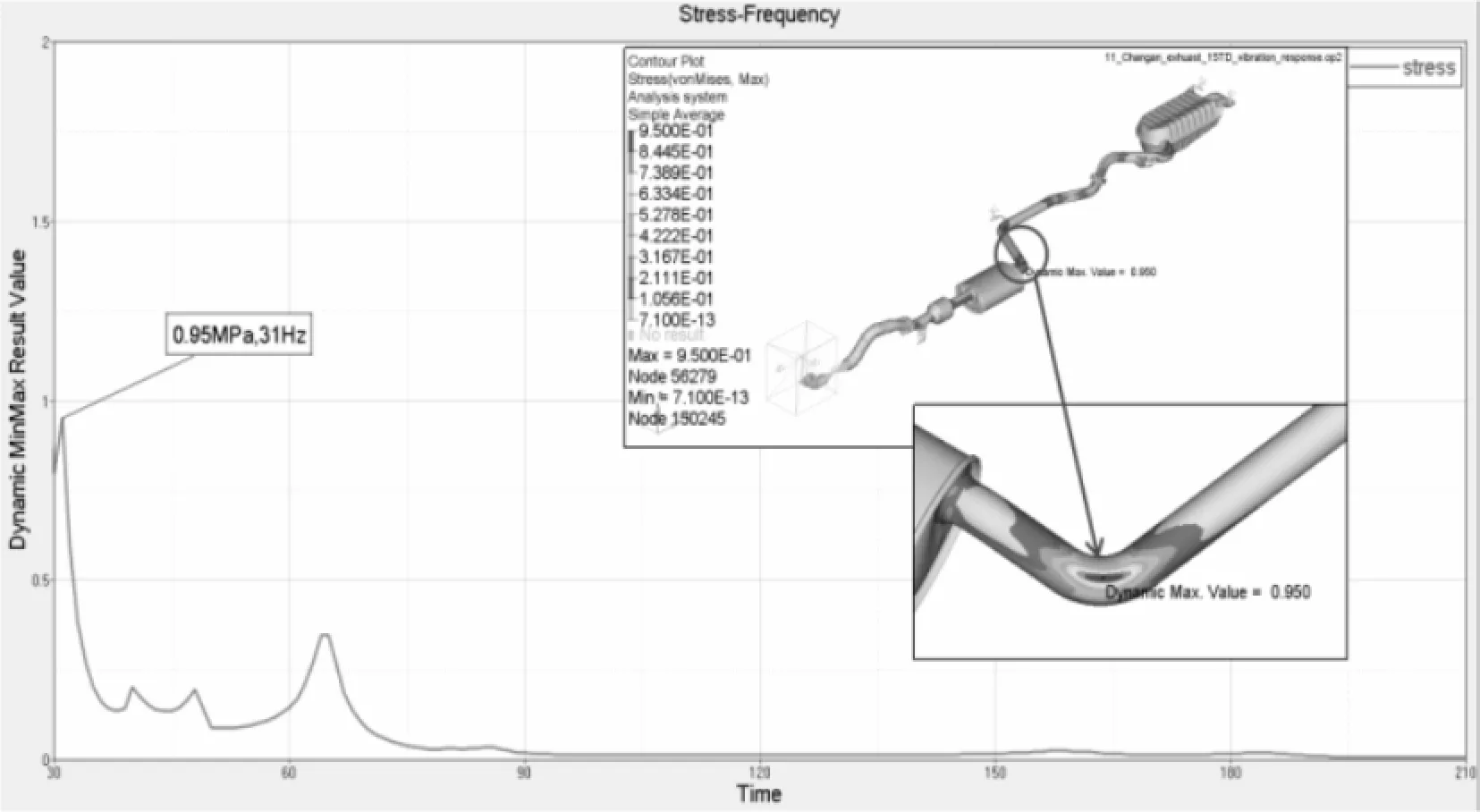
图10 排气系统应力分析曲线界面图
4 吊钩结构、悬挂点设计分析与优化
4.1 吊钩约束模态分析
根据企业设计要求,吊钩约束模态目标值为480 Hz,如果吊钩约束模态低于480 Hz。此时的吊钩约束模态易与整个排气系统约束模态产生共振,会加大吊钩振动位移与传递力,进而影响整个排气系统的疲劳性能和噪声。而当吊钩约束模态大于480 Hz时,可有效地避免共振现象。因此,对排气吊钩单独做约束模态分析是非常必要的,也是用来校核吊钩约束模态是否达到目标值要求的有效方法。由图1可知排气吊钩的编号与悬挂位置,分别截断吊钩前后180 mm,约束其前后断面6个自由度,吊钩约束模态有限元模型,如图11所示。

图11 吊钩约束模态有限元模型
由图12~图16可知排气吊钩约束模态分析结果,其中3号吊钩约束模态为463.9 Hz,低于企业设计目标值480 Hz,需对3号吊钩进行优化处理。其他吊钩约束模态均达到目标值要求。

图12 1、2号吊钩约束模态分析结果(707.5 Hz)
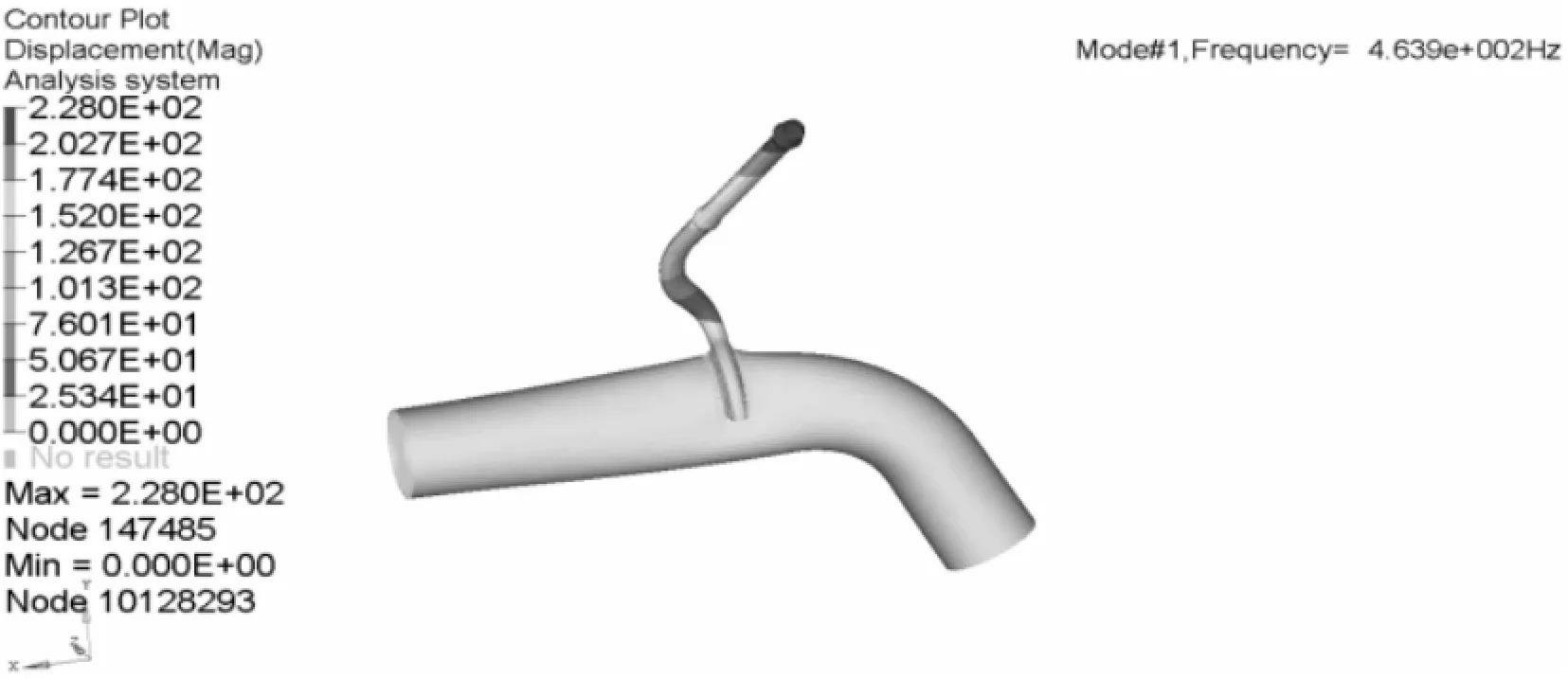
图13 3号吊钩约束模态分析结果(463.9 Hz)

图14 4号吊钩约束模态分析结果(513.6 Hz)
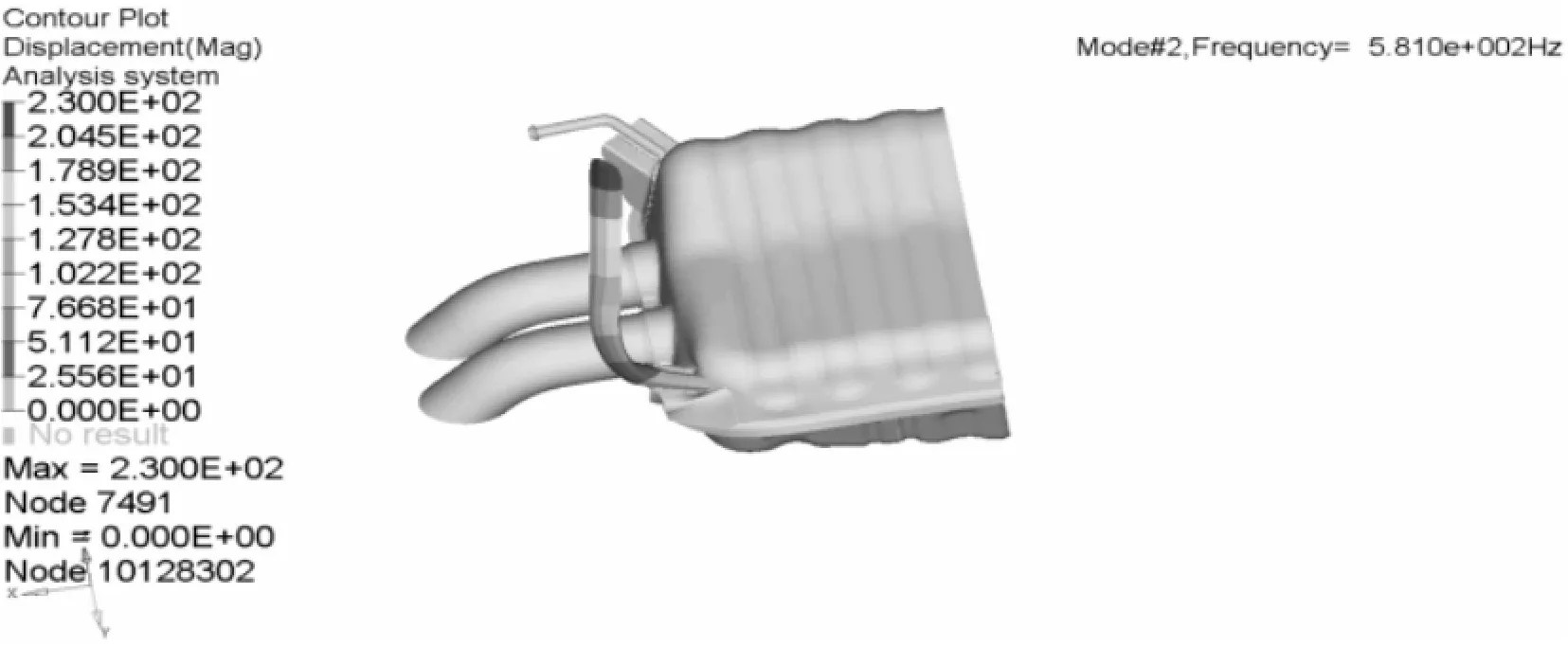
图15 5号吊钩约束模态分析结果(581.0 Hz)
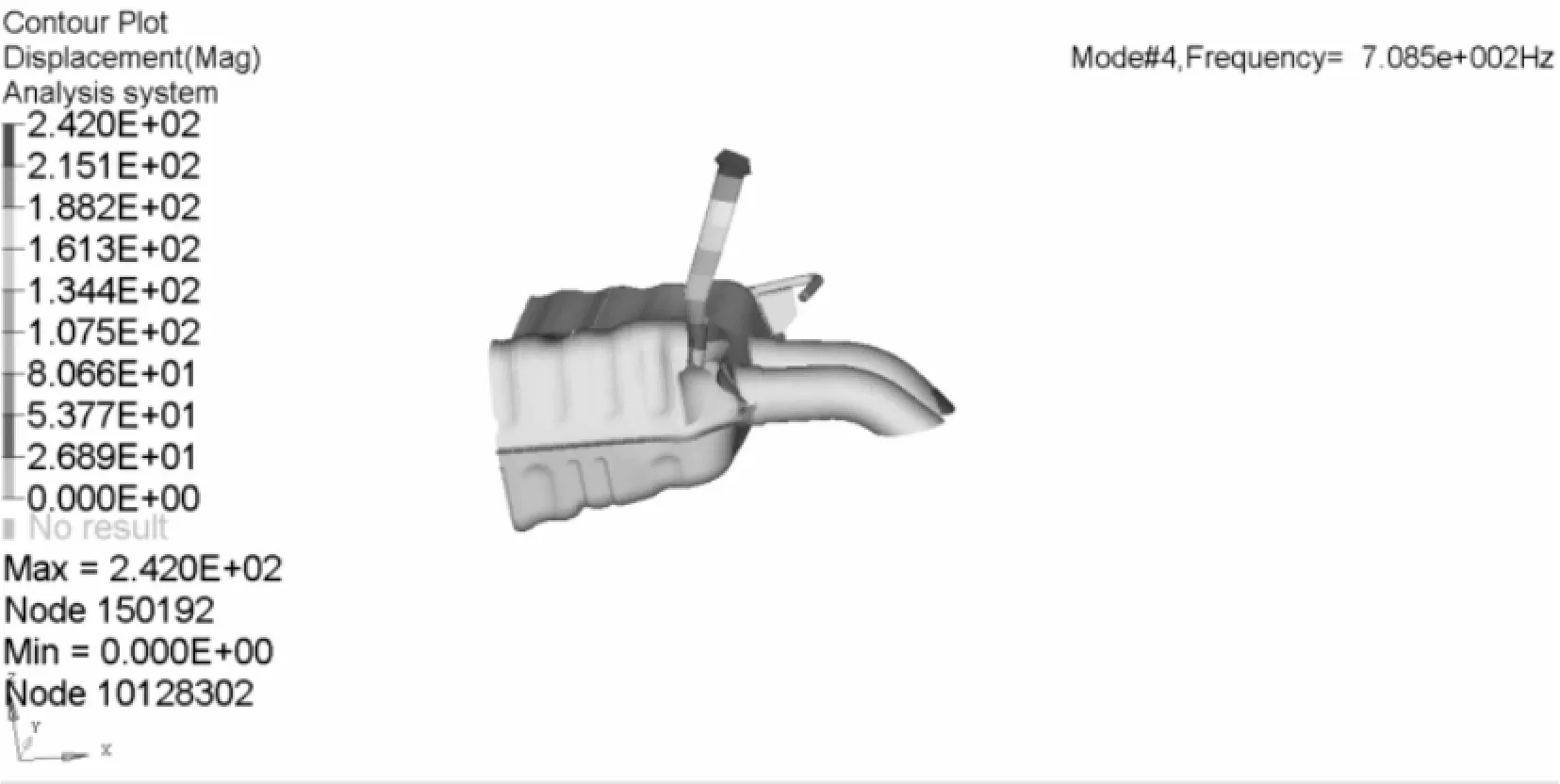
图16 6号吊钩约束模态分析结果(708.5 Hz)
4.2 吊钩结构优化
根据3号吊钩约束模态分析结果,制定优化方案:在其旁边增加一个L型挂钩,并进行焊接,如图17所示。对优化后的3号吊钩有限元模型再次做约束模态分析,分析结果与优化前进行对比。分析结果显示,优化后的吊钩约束模态为599.9 Hz,如图18所示,符合企业目标值要求。
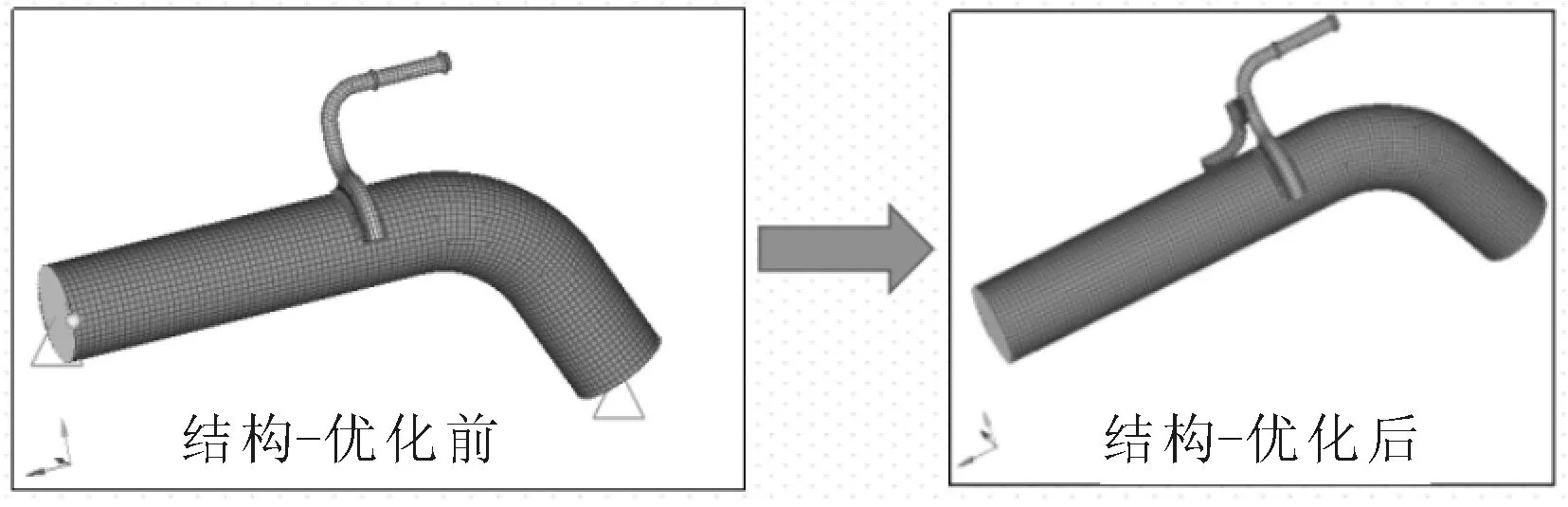
图17 吊钩结构优化前后对比

图18 吊钩结构优化后模态分析对比
4.3 吊钩位置优化
为了确保排气系统的振动能量传递到车身是最小值,减小排气系统对整车NVH性能的影响,因此,需要验证吊钩位置选择的合理性[10]。笔者采用ADDOFD(平均驱动自由度位移法)来确定排气系统悬挂点的位置。在ADDOFD方法中,定义第j个自由度的平均驱动自由度位移为:
(2)
式中,φjr为第j个自由度在第r阶模态的振型系数;ωr为第r阶激励频率;N为所求的模态数[11]。
优化方案为:根据排气系统与汽车底盘空间匹配情况,沿排气系统X轴间隔20 mm挑选挂钩布置的潜在点,共169个点,编号依次为001~169;通过Optistruct得到频率范围在前200 Hz内的全部模态振型,进而得到这169个点位置位移值,再经过计权累加,计算ADDOFD值。计算后作出散点图,如图19所示,波谷位置和附近区域就是吊钩位置选择的最佳悬挂点,其中虚线代表企业设计时吊钩的原始位置,实线代表优化后吊钩的位置。
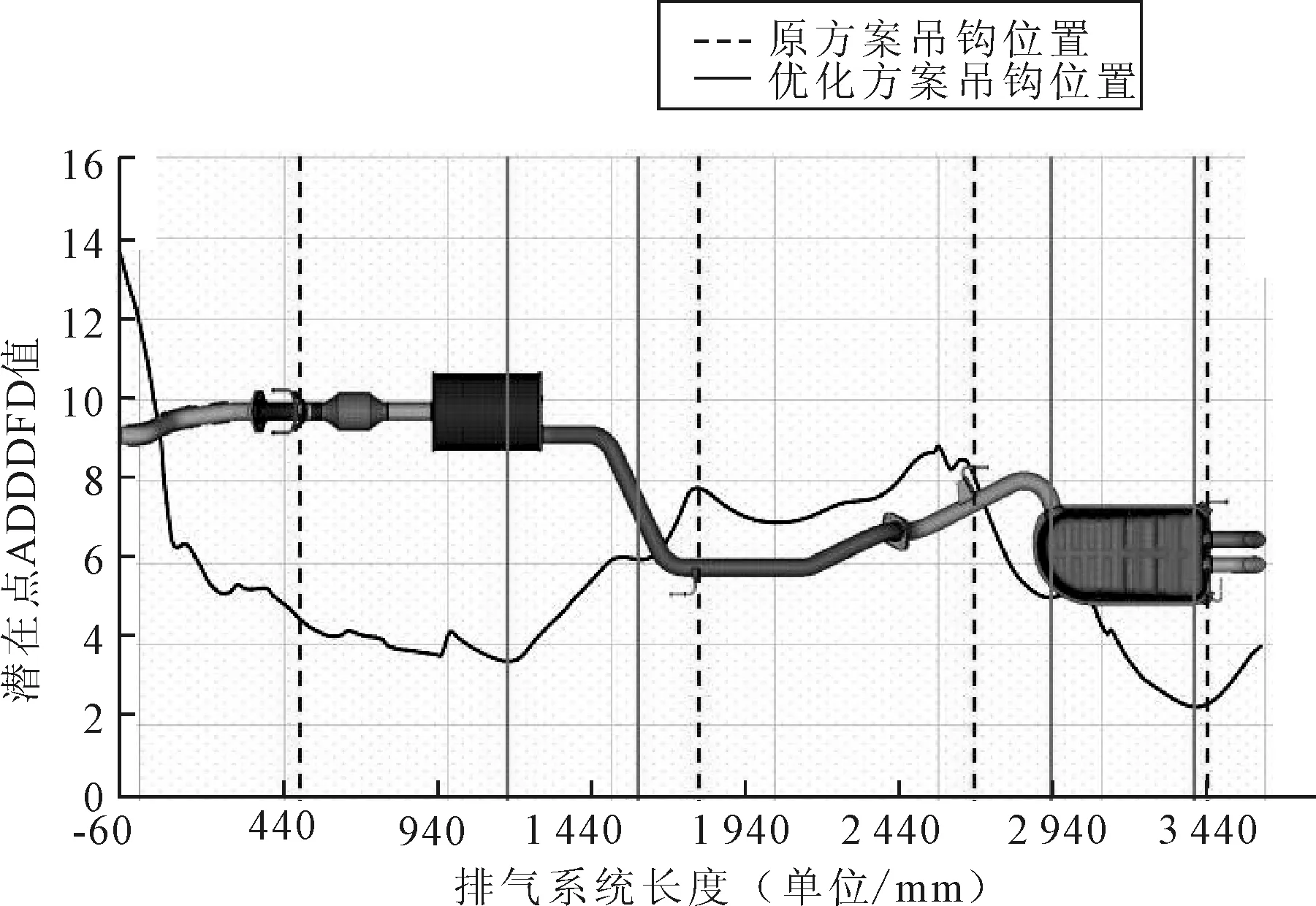
图19 ADDOFD值散点图
5 结论
(1)对某商用车排气系统进行自由模态分析,并进行了仿真值与试验值的对比,验证了有限元模型的合理性;
(2)对排气系统容易造成机械振动和噪声的原因逐一进行分析排查,经过仿真,静力学、动力学、传递力及位移响应分析均满足设计要求;
(3)根据企业要求,针对吊钩位置进行了约束模态分析,计算出3号吊钩约束模态为463.9 Hz,低于企业要求的目标值480 Hz,其他吊钩位置均满足要求;
(4)对3号吊钩存在的问题进行结构优化,并采用ADDOFD方法确定了排气系统悬挂点的最优位置位置,然后再次进行约束模态分析,其值为599.9 Hz,达到了企业要求。
