高速流场下非破坏挖掘抽吸车叶轮的应力应变分析

肖 遥，宋春生,黄向阳,闫炳雷

(武汉理工大学 机电工程学院，湖北 武汉 430070)

非破坏挖掘抽吸车是一种通过高压叶轮系统产生强大吸力来进行挖掘及运输的非破坏性施工车辆。利用空气动力抽吸车把土从地面抽吸上来，实现土壤、砂石、粉料等物料的挖掘，对市政非破坏施工具有很高的应用价值[1]。

在非破坏性挖掘抽吸车作业过程中，叶轮部分会承受由于高速旋转而产生的离心作用力以及高速气流产生的压力，由于叶轮转速非常高，叶片会受到到很大的应力而导致变形，甚至是断裂，对其工作寿命产生极大的影响[2]。非破坏挖掘抽吸车作为一种新型的施工车辆，目前国内外对它的研究不多，针对适用于非破坏挖掘抽吸车的叶轮的研究也不多。国内外对叶轮的研究主要集中在叶轮的结构设计方法[3-6]、叶轮的内流场分析[7-9]以及叶轮的性能参数[10]，且研究的叶轮大多处于中低速，对高速叶轮的研究很少。非破坏挖掘抽吸车的叶轮转速很高，为了保证叶轮结构的安全性，对其进行流场分析，然后将得到的流场分布以载荷的形式与高速转动所产生的离心作用力一起加载到叶轮上，对其进行应力应变分析，为非破坏挖掘抽吸车叶轮的设计提供理论指导。

1 叶轮模型的建立与内流场分析

1.1 模型建立

研究对象采用某型号非破坏抽吸挖掘车的叶轮，其具体的参数如表1所示。

表1 叶轮的参数

图1 叶轮模型

在SolidWorks中建立叶轮的三维模型，如图1所示。为了在计算中区分静止的蜗壳区和旋转的叶轮区，在模型处理时将完整模型分割为3部分：入口区、叶轮区和出口区，3个区域独立生成网格，在Fluent中进行组装，并通过interface边界交换流场信息。由于叶片弯曲排布的方式，以及叶轮模型较为复杂，使得结构网格生成困难或者生成的网格质量太差，因此本次计算采用混合非结构网格，这种类型的网格可以在模型简单区域生成结构网格，在复杂区域用非结构网格进行过渡，既保证了较好的网格质量，又保证了计算精度。网格生成采用POINTWISE软件，该软件可灵活处理各种复杂模型。图2为叶轮系统的网格模型。

图2 叶轮系统网格模型

1.2 计算参数

本次计算采用fluent并行计算，采用旋转坐标系MRF(moving reference frames)方法模拟叶轮转动时的流场。

(1)控制方程。由于叶轮转速高，流动速度高，因此采用fluent密度基求解器求解粘性可压缩N-S方程，气体属性设置为理想气体(ideal gas)，湍流模型设置为k-ε模型。

(2)边界条件。入口边界设置为质量流量入口(mass flow inlet)，流量设置为8.183 kg/s(由表1中给定的入口流量乘以空气密度而得)，初始静压设置为101 325 Pa，即一个标准大气压。出口边界设置为压力出口边界(pressure outlet)，设定标准大气压为出口边界值。

Interface边界设置在入口区域与叶轮区域交界面，以及叶轮区域与出口区域交界面。用于流场信息插值。

物面边界设置为无滑移物面边界，其中叶轮物面设置为旋转物面，转速与叶轮区域流场一致，其余物面为静止物面。

叶轮区域设置为旋转坐标系，输入叶轮转速。

1.3 内流场分析

首先对叶轮在额定转速n=4 000 r/min时的计算结果进行分析，得到了该叶轮额定转速时的内部流动特点，验证了模型的正确性；非破坏挖掘抽吸车叶轮的高转速与常规叶轮的转速有一定的区别，为了进一步研究转速对叶轮内流场的影响，分析了叶轮的转速分别1 000 r/min、2 000 r/min和3 000 r/min时的叶轮内流场变化。

(1)额定转速下的压力场分析。为了方便研究，取z=50 mm截面作为分析对象。

图3分别给出了z=50 mm处的平面静压和全压分布图。通过图3(a)中的压力场分布可以看出，叶轮内部的静压沿着半径方向往外逐渐增大，并且在叶轮内部流场中的静压没有达到最大值，在叶轮的出口处，气体静压会陡然增大，产生一个类似“突变”的效果，经分析可能是因为当气体从叶轮内部流向出口的交界处时，气体流动的空间变大，扩压减速导致的。图3(a)中较为清晰地反映出叶轮内部的压力是不对称的，离喉部越近，叶片的吸力面压力越低，因此低压区也越大。

图3 叶轮的静压和全压

从图3(b)中可以看出叶轮内部的全压总体来说变化比较平稳，会在叶片处形成一小块的高压区，很明显是由于高速旋转的叶片对气体的作用而形成的。从仿真结果可知，最大全压约为28 560 Pa；由设计计算得到的理论全压为27 317 Pa，因此可以计算出理论的全压与仿真得到的全压的差值约为1 243 Pa，误差约为4.56%，因此模型是可靠的。

(2)额定转速下的速度场分析。如图4所示，在叶轮的内部流场中，叶片附近的气流速度会沿着半径方向向外逐渐增大，在叶轮与蜗壳交汇的喉部处会出现一段高速气流，这是在气体流出的过程中与蜗壳的管壁发生作用而形成的，蜗壳的管壁对高速气流形成的阻碍作用。

图4 叶轮的速度云图和速度流线图

(3)改变叶轮转速的流场分析。通过对不同转速情况下的综合对比，转速的变化对静压的影响显著，转速越大，内部静压越高，这点在图5中可以非常直观地看出，同时发现当转速处于中低速(转速小于等于3 000 r/min)时，转速越大，静压虽然会变大，但是涨幅比较稳定，当转速处于4 000 r/min的高转速时，叶轮的静压相对之前会发生突然增大的现象；另一方面，不管转速多大，叶轮内部静压分布并不具有很好的对称性，这是由于蜗壳的存在导致静压呈现不对称性，且转速越高，不对称性越明显，最大静压出现在出口的上方，最小静压出现在叶轮入口处，而且出现的位置并不是绝对的，会随着转速的变化而发生变化。这种不对称的分布情况，会严重影响叶轮在旋转中的动平衡。

图5 静压与转速的变化关系

2 叶轮的应力应变分析

非破坏挖掘抽吸车的叶轮在工作中主要受到两个力的作用：高速旋转而产生的离心作用力和由于高速流场而产生的压力。由于叶轮的变形不大，因此本次仿真分析采用单向流固耦合的分析方法，忽略叶轮变形对流场的反作用。为了探究高速流场对于叶轮变形的影响程度，本次仿真主要分为两个部分：仅考虑离心力作用时的叶轮应力应变分析和同时考虑离心作用力与高速流场载荷条件下的叶轮应力应变分析。

2.1 仅考虑离心作用力的应力应变分析

仅考虑离心力的作用，设置n=4 000 r/min，选取轴孔表面作全自由度约束，计算得到的叶轮与叶片的等效应力如图6所示，叶轮与叶片的应变情况如图7所示。

图6 叶轮和叶片等效应力图

从图6中可以看出，叶轮受到的最大等效应力大小为495.01 MPa，最大等效应力的位置出现在叶轮轮盘与叶片的连接处，并且不难发现该部位也是应力集中的部位，其产生的原因主要是因为叶轮与叶片根部的连接角度为内直角，并且材料厚度也发生了一定的变化，因此很容易产生应力集中，另一方面是因为轮盘与叶片的连接工艺属于焊接工艺，而焊接也很容易造成应力集中的情况。除应力集中出现的情况之外，叶轮受到的等效应力不大，最大约为300 MPa左右，并且呈现由中心向外逐渐减小的趋势。

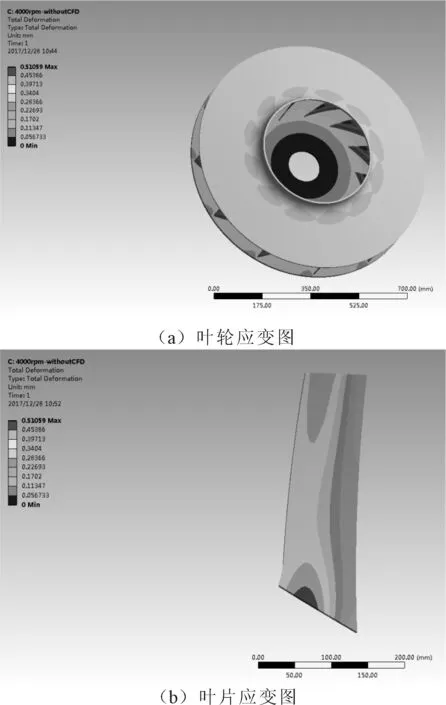
图7 叶轮和叶片应变图

图7为叶轮的叶片在应力作用下的应变，从图7(b)中可以很清晰地看到最大应变发生在叶片根部，也即叶片与叶轮的连接处中间，其最大变形量约为0.511 mm，说明在叶轮高速旋转的过程中，叶片根部与叶轮的连接处受到的应力最大，其形变量也最大，这个结论与从图6等效应力曲线的变化趋势一致，符合实际情况。从图7(a)中可以看出叶轮轮盖、轮盘等部位的形变量比较一致，且形变量很小。

2.2 同时考虑离心作用力与高速流场载荷和应力应变分析

设叶轮的转速n=4 000 r/min，将流场分析得到的气动载荷导入到静力学分析模块中，并作为叶轮表面载荷加载到应力分析模型中进行计算。计算结果如图8所示。

图8 叶轮和叶片等效应力与应变图

从图8可以看出，叶轮受到的最大等效应力值约为501.31 MPa，最大应变量约为0.537 mm，其受力与形变的整体趋势与图6和图7中仅考虑离心力情况下得到的结论一致。通过简单的计算可以得到叶轮所受到的等效应力主要是由离心作用力的大小决定的，离心作用力的影响约为98.7%，远远大于高速流场载荷带来的应力；另一方面，叶轮的形变量也主要由离心作用力决定，其影响约占95.1%，其余部分则是由流场载荷带来的。

2.3 不同转速下的叶轮应力应变分析

为了对比分析不同转速下的叶轮变形情况，本次仿真对其他3种转速下的叶轮应变情况进行了仿真分析，得到叶轮应变与转速的关系如表2所示。

表2 叶轮应变与转速的关系

从表2可以看出，当转速增加时，叶轮的最大应变值是不断增大的，但是这种增大与转速的增量并不是线性关系。叶轮的转速越大，离心力与气动载荷的影响也就越大，其应变也会越大。

3 结论

非破坏挖掘抽吸车的叶轮处于高转速的状态之下，而高转速叶轮的内流场与中低速叶轮的内流场存在一定的区别，并且高速流场对叶轮应力应变的影响也会变大。笔者对叶轮的内流场进行仿真分析，得到了内流场压力分布与速度分布的特点，针对叶轮的使用要求设置了另外3组转速进行对比分析，得到如下结论：(1)转速越高，叶轮的静压越大，但是对内流场的分布影响不大，在转速由低速到高速的变化过程中，内部的流场会产生突然增大的现象；(2)通过计算对比，得到叶轮所受到的等效应力主要是由离心作用力的大小决定的，离心作用力的影响占98.7%，远远大于高速流场载荷带来的应力；另一方面，叶轮的形变量也主要是由离心作用力决定，其影响约占95.1%，剩余的4.9%则是由流场载荷带来的形变。因此，高速流场载荷对于叶轮的变形的影响微乎其微，远远小于叶轮自身旋转产生的离心力所带来的影响，在大多数场合下可以忽略不计。