等离子体鞘套电磁散射特性的场离散蒙特卡罗仿真

贾洁姝， 梁子长， 何鸿飞

（电磁散射重点实验室，上海200438）

0 引言

飞行器超高速飞行时，与周围大气相互作用产生等离子体鞘套。鞘套中的带电粒子发生碰撞会造成能量的损耗，对飞行器的电磁散射特性产生严重影响［1-3］。随着飞行高度及马赫数的变化，目标周围所形成的绕流流场参数及电参数分布也发生改变，所呈现的目标雷达特征信息是不同的［4-5］。等离子体鞘套是影响探测超高速飞行器的重要因素。

超高速目标流场网格一般几倍于目标尺寸，其网格数量较多。对等离子体中局部分层界面电磁波的计算，采用射线跟踪方法需要进行射线分裂。对复杂的流场网格，该过程将十分复杂，计算效率也将下降。为解决这一问题，本文引入了蒙特卡罗方法（Monte Carlomethod），计算等离子体包覆目标电磁特性。

1 仿真建模

蒙特卡罗方法是一种以概率统计理论为指导的数值计算方法，在粒子输运计算、热力学、光学以及空气动力学等领域应用较为广泛。由于蒙特卡罗方法是一种非确定性的算法，模拟对象需粒子化，在电磁散射计算领域，主要用于随机环境的散射模拟，且主要基于能量离散电磁波粒子开展计算。

首先，以等离子体流场网格外表面为模拟电磁波粒子的入射面，在该入射面内，电磁波粒子的起始位置呈随机分布，粒子起始运动方向由电磁波源指向其起始位置。对每一电磁波粒子，假定在等离子体中的运动步长为Δl，则每前进一步，电磁波粒子位置变化Δζ及运动方向的变化Δθ分别如式（1）与式（2）所示。

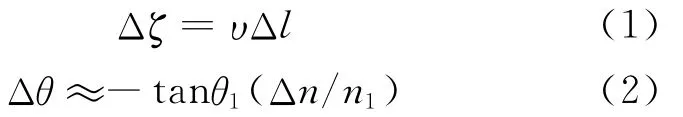
式中：θ1为局部电磁波粒子前进方向υ与等离子体等效折射率变化梯度方向ζ的夹角；Δn为粒子向前行进一步对应的等效折射率变化；n1为该位置处等离子体的等效折射率，在等离子体鞘套外表面处n1≈1。

然后，计算每前进一步电磁波粒子的吸收概率pa，如式（4）所示。

式中：a1为该位置处等离子体的等效吸收系数。利用计算机生成0至1间的伪随机数，当该随机数小于pa，则电磁波粒子被吸收。

再计算运动一步后电磁波粒子位置ζ1以及等效折射率n2，分别如式（5）与式（6）所示。

若n2＞0，电磁波粒子运动方向由式（7）计算。

式中：t为单位矢量，其方向为υ与ζ所在平面内垂直于ζ的方向。

若n2≤0，则电磁波粒子运动方向发生全反射，如式（8）所示。

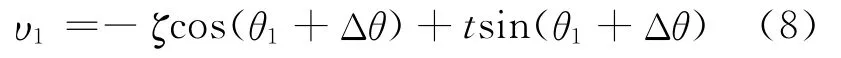
重复上述过程，直至电磁波粒子从等离子体网格外表面离开或被吸收。

重复以上过程，直至被吸收和被反射的电磁波粒子数与总入射粒子数的比值趋于稳定，一般要求该比值偏差小于10%。

等离子体包覆目标的RCS由被反射的电磁波粒子与入射粒子总数的比值计算，如式（9）所示。

式中：N为入射粒子总数，N越大，单个电磁波粒子表示的电场幅度越小，电场幅度在粒子传播过程中保持不变；ΔEsi（θ）表示某观测方向下接收的第i个散射粒子电场，其中包含路程相位和目标反射相位；M表示该方向散射粒子的总数。

与其它计算方法相比，该方法具有以下优点：

a）适于复杂三维非均匀连续分布的等离子体及其包覆目标的电磁特性计算；

b）适于并行化计算，计算耗时与电磁波频率相关性较小，可计算电大尺寸等离子体包覆目标的电磁特性；

c）可共用流场仿真网格，减少了计算网格转换对电磁计算精度的影响。

2 收敛性分析

由于统计仿真方法存在涨落噪声，MC方法计算等离子体目标的RCS需进行收敛性分析，即分析不同模拟粒子数对RCS结果的影响。这里以飞行马赫数为15的钝锥体5 GHz的RCS数据为例，按RCS峰值区域和谷值区域分别进行收敛性分析，如图1和图2所示。

图1 钝锥体RCS峰值区域的收敛性分析

在RCS峰值区域，当模拟粒子数由3万增加至60万时，等离子体覆盖目标的RCS计算结果趋于稳定，如图1（b）所示。在RCS谷值区域，当模拟粒子数由1万增加至60万时，涨落噪声略有降低，RCS计算结果趋于稳定，如图2（b）所示。可以看出，MC方法收敛性在RCS谷值和峰值区域有较大区别，在RCS谷值区域，粒子数的收敛性较慢，而在RCS峰值区域粒子数的收敛性十分快。

图2 钝锥体RCS谷值区域的收敛性分析

3 典型超高速目标模型RCS计算分析

采用上述的MC方法，对钝锥体典型超高速目标计算其不同频率、观测角下的RCS，并对其中主要目标RCS衰减、增强等现象进行了分析。由于对称性，流场网格仅提供一半网格，以下计算的RCS结果也仅考虑上半部分网格，实际目标的RCS应增加约6 d B。

钝锥体模型长为0.5 m，底面直径0.33 m，如图3所示。等离子体流场区域尺寸约为2.1 m×1.6 m×0.8 m。目标飞行马赫数选取15和20，飞行高度为75 k m。以下分析不同频率及方位角对RCS的影响。

主要计算参数：俯仰角为90°，即观测面处于XOY面（即对称面）内；模拟入射粒子数为10万；模拟粒子运动的最大步数为300。计算采用了6核并行，平均每频点耗时约1.3 h。

图3 钝锥体模型

飞行马赫数为15时，对比有无等离子体时钝锥体RCS的变化，如图4所示。频率1 GHz在方位角20°附近，2 GHz在方位角5°附近，后向RCS出现无值情况，对应完全的折射隐身现象。

同时，在频率2 GHz、方位角20°以及频率3 GHz、方位角10°附近，由于折射偏转作用，目标底部镜面反射方向发生偏转，斜入射下目标RCS增强约10 d B，如图4（b）与图4（c）所示。另一方面，随着频率的增加，由于等离子体分布噪声将导致一定的传播路径相位起伏，方位角60°附近较大范围的目标RCS谷值增加，但RCS值仍较小。

由图4可以看出，在方向角180°的头部方向，由于钝锥体结构特点，这个方位本身RCS相对而言较小，加上头部等离子体较高、吸收作用较大的原因，不同频段下其RCS减小相对较大。方向角0°和100°方向是两个明显的反射方位，其反射较大。方位角100°附近由于入射方位与锥体侧面近似垂直，所以反射较大。当频率不大于5 GHz的情况，在方位角0°的尾部方向，由于等离子体的折射偏转作用，钝锥体RCS存在较大减小，甚至完全隐身；随着频率增大，等离子体鞘套对目标RCS的影响逐步降低，目标非镜面反射方向的RCS逐步增加，这是由于等离子体密度的非均匀性导致反射增强。

图5给出了目标飞行马赫数为20时，不同入射电磁波频率有无等离子体时钝锥体RCS的对比变化，实线为等离子体覆盖目标的RCS变化情况，虚线为目标本身的RCS变化情况。等离子体对目标RCS的缩减及增强影响均十分明显，尤其是入射电磁波频率为5 GHz时，在较宽方位角范围内等离子体对目标RCS影响明显。图5（b）、图5（c）分别为10 GHz、18 GHz频率下RCS结果对比，模拟入射粒子数增加至60万。

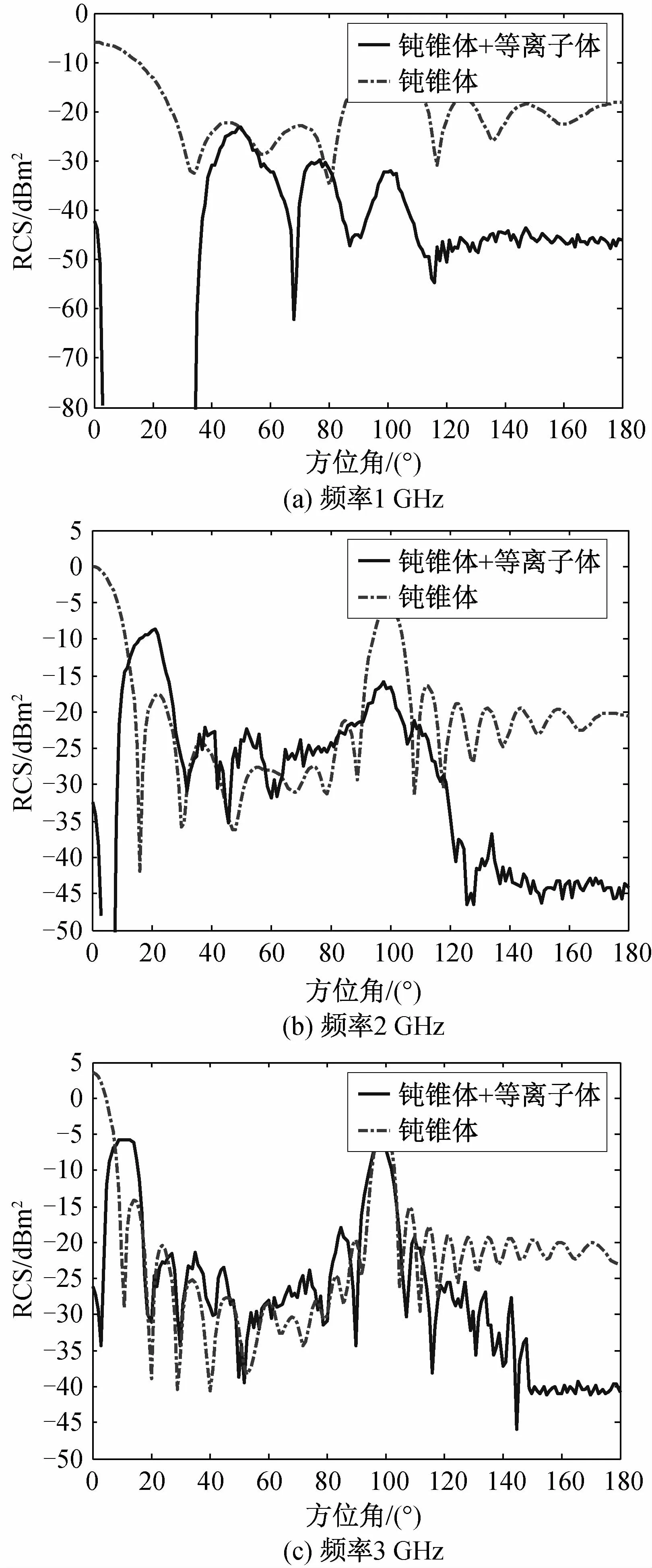
图4 飞行马赫数为15时不同频率及方位角的RCS分布

由图5可以看出，等离子体覆盖目标后，在方位角20°至80°方向，等离子体鞘套目标RCS较钝锥体目标本身略大，这主要因为等离子体层局部密度的差异，导致目标光滑表面“粗糙化”，散射相对增强；而在方位角100°至180°方向，由于等离子体吸收作用，等离子体鞘套目标RCS较钝锥体目标本身RCS缩减。

图5 飞行马赫数为20时钝锥体不同方位角的RCS分布

4 结论

针对高超声速目标等离子体鞘套电磁特性仿真的难点，本文采用场离散的MC方法，仿真得到了等离子体覆盖目标的电磁特性，并结合钝锥体目标及等离子体鞘套目标RCS对比，分析不同频率下RCS与入射方位角的关系，分析给出了等离子体对目标RCS的主要缩减及增强机理。MC方法可以对等离子体流场仿真结果进行自动化处理，便于超高速目标流场-电磁场的一体化仿真建模，可实现等离子体包覆的电大尺寸目标的电磁散射特性的快速计算。