改进的毫米波SFCW雷达多目标检测算法

黄 梁， 朱 莉， 刘 婕

（南京理工大学 电光学院 探测与控制工程系，南京210094）

0 引言

近年来，毫米波技术在雷达领域得到了广泛的应用［1］。与微波相比，毫米波具有精度高、抗干扰能力强、天线尺寸小等特点。随着毫米波器件的突破，毫米波系统的研究和应用得到了长足发展。

连续波雷达通过向被测目标发射连续波信号检测目标的距离和速度信息，且可实现高精度无模糊测距、测速［2］。

步进频连续波雷达是一种发射频率步进连续波信号的多频连续波雷达，可以分辨出固定目标与移动目标，并完成多目标的测量工作［3-4］。

1 步进频连续波多目标算法

步进频连续波雷达按发射信号主要分为锯齿波（单正程）和三角波（双程），这里采用锯齿波［5］。

顺序发射M个等间隔频率的正弦连续波，基频为f0，每个频率的持续时间为Tp，频率间隔为Δf。发射波形如图1所示。

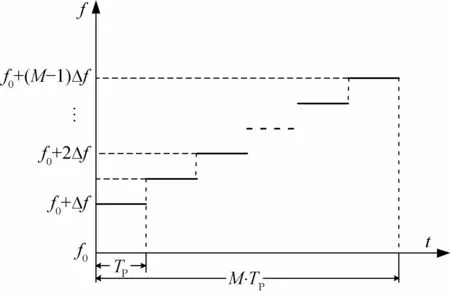
图1 锯齿波发射波形

设每个频率的发射信号为

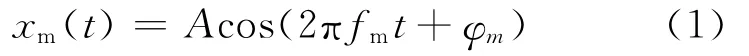
式中：fm=f0+mΔf为发射频率，M=1，…，M-1。

假设总共有I个目标，则频率fm的回波信号经接收机混频、相干检波、采样处理后，对零中频采样序列进行N点FFT变换，得

式中：Ai为第i个目标的回波幅度；wdmi=2πfdmiTs；Ts为采样频率；Tp为每个频率的发射时间。k满足k=0，1，…，N-1。对于每个频率的回波信号经过FFT后都输出一组N个复信号，总共M 组［6］。

对于式（2），对其幅度谱|X（k）|峰值搜索可得［7-8］

式中：kmax为幅度谱峰值所在的坐标。

可得所有目标的速度为

式中：fs为采样频率；λ为雷达工作波长。

速度分辨率为

然后将FFT后输出的M组中属于同一速度单元的复信号，进行取模，并将其相加后送入恒虚警CFAR单元检测［9-10］。若检测过门限值，则说明该速度单元有目标。

然而对于有目标的速度单元，还无法确定目标个数以及每个目标的距离信息，需要进一步的处理。

假设速度单元v经过恒虚警检测输出“1”，即速度单元上有目标。回波信号FFT模块输出的M组N个复信号如表1所示，现在从中取出对应在速度单元v上的那组M 个复信号值，然后对取出的M个复信号进行相位补偿，再进行逆FFT变换。最后对逆FFT变换得到的M个复信号取模并送入距离门限检测从而得到该速度单元上有几个目标以及每个目标的距离信息。

表1 M组N个复信号的FFT结果表

假设一个周期内的发射信号为f1，f2，…，fM，且在某一个速度单元v上有i个目标，则发射频率为fm的回波信号为［11］

对Xm（kmax）先进行相位补偿，消除时延引起的距离相位项，得

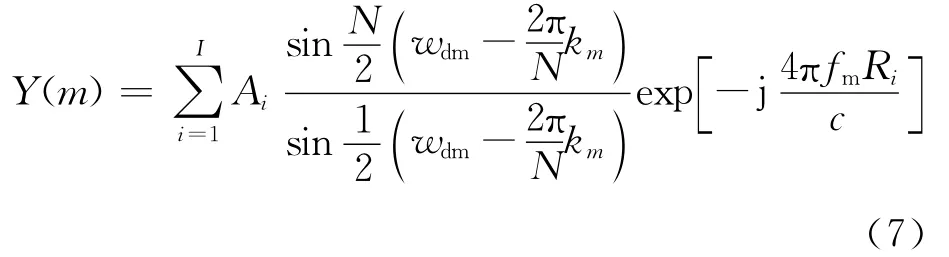
对Y（m）进行离散傅里叶逆变换，得

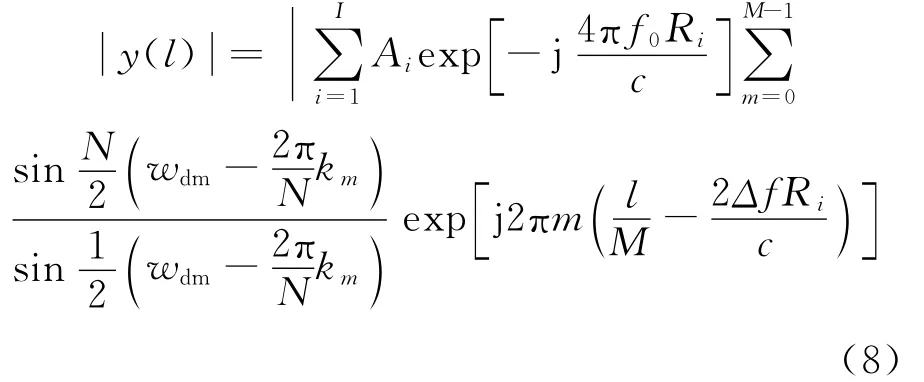
由上式可以看出，共有I个峰值，即在速度单元v上有I个目标。

设l=li时，li/M=2Δf Ri/c，则|y（l）|达到峰值。距离公式为

距离分辨率公式为

测距范围为

2 改进算法

由于测速只利用了单个频率的FFT，相参积累的时间短，降低了速度分辨率。这里采用发射多个周期为T的步进频率连续波来进一步研究。

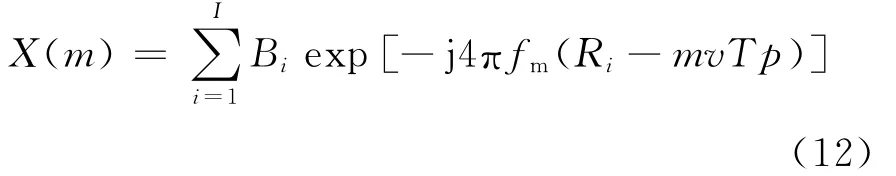
其中：

考虑到发射N个周期的步进频率波，则

式中：n满足n=0，1…，N-1，对任意两个周期进行相位差，可得

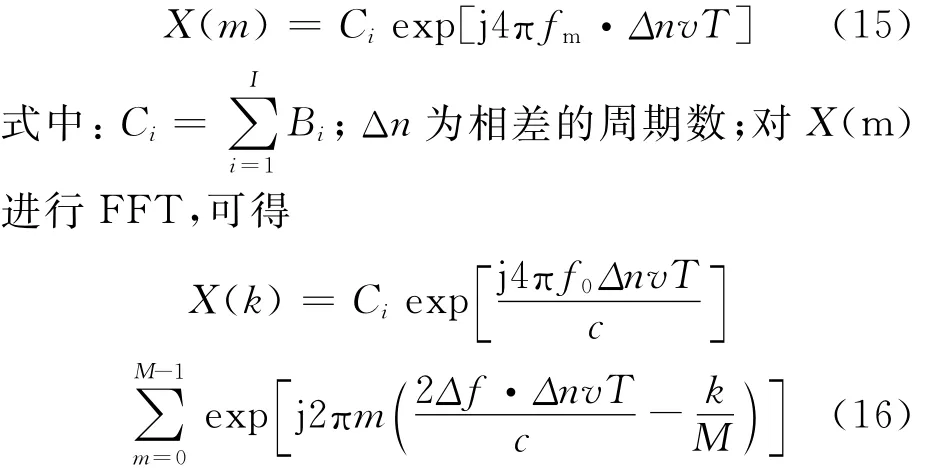
对上式的幅度谱进行峰值搜索，可得

速度分辨率为

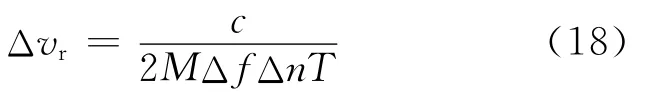
由于利用了时延引起的距离项信息来求取速度，所以该速度分辨率与利用单频多普勒信息求取的速度分辨率相比，有影响结果的参数更多。设基频f0为30 GHz，采样频率fs为0.5 MHz，FFT点数为1 024，则利用单频多普勒信息的速度分辨率约为2.44 m/s。设M为1 024，频率步进值Δf取150 k Hz，T取37.5μs，则要想达到利用单频多普勒信息求取的速度分辨率，只需要Δn≥21即可。另外，由于该速度分辨率与距离分辨率有相同的参数M和Δf，所以在提高距离分辨率的同时也能提高速度分辨率。

3 仿真结果

仿真中取基频f0为30 GHz，步进频率Δf为150 k Hz，每个步进频率持续时间Tp为37.5μs，步进频率个数M为1 024。由式（10）和（11）可得距离分辨率为0.976 m，最大测距范围为1 000 m。

第1组仿真设有两个速度相同，但距离不同的目标。速度为100 m/s，距离分别为100 m和200 m。仿真结果如图2所示。

图2 两个速度相同，距离不同目标的距离-幅度图

由图2可以看出，在距离100 m和200 m处分别有一个目标，说明已经分辨出了两个速度相同的目标。

第2组仿真设有五个目标，速度分别为150 m/s，189 m/s，189 m/s，235 m/s，311 m/s，距离分别为50 m，100 m，159 m，234 m，590 m。改进采用了64个周期的发射信号，取Δn为50。仿真结果如图3及图4所示，表2及表3为仿真数据。

图3 五个目标的速度-幅度图

图4 五个目标的距离-幅度图

由图3可以看出有4个不同的速度值，据此可以划分为4个速度通道进行分析。由图4可以看出能够找到5个目标，且其中有两个目标的速度相同。表2及表3分别是这5个目标的速度距离误差情况，经过计算，对于单周期的速度误差平均值为0.473%，而改进多周期的速度误差平均值为0.114%，改进算法的速度误差减小了约4倍。因此，算法对于多目标检测有较好的准确性。

表2 五个目标的速度仿真数据

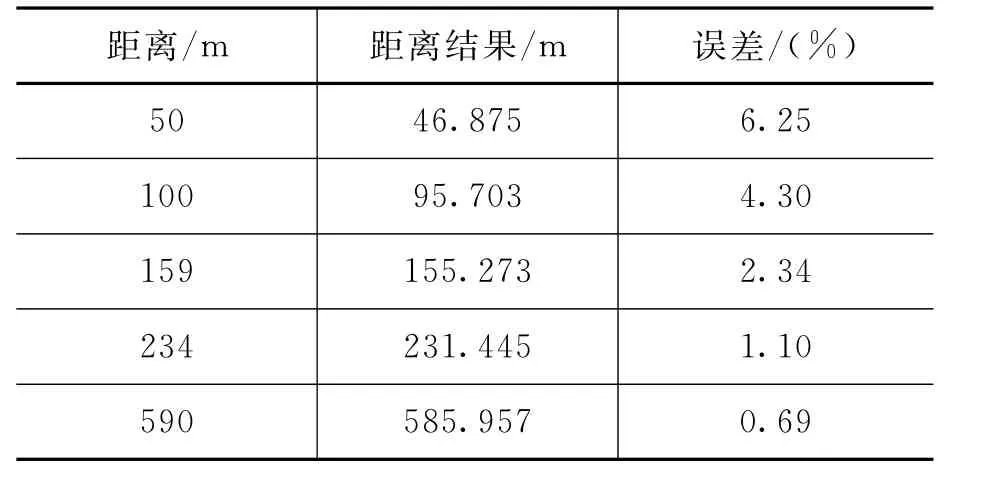
表3 五个目标的距离仿真数据

第3组仿真，提高步进频个数M为2 048，采用64个周期发射信号，取Δn为50。设两个速度不同的目标，距离不同的目标，速度分别为189 m/s和235 m/s，距离分别为100 m和234 m。仿真数据见表4。

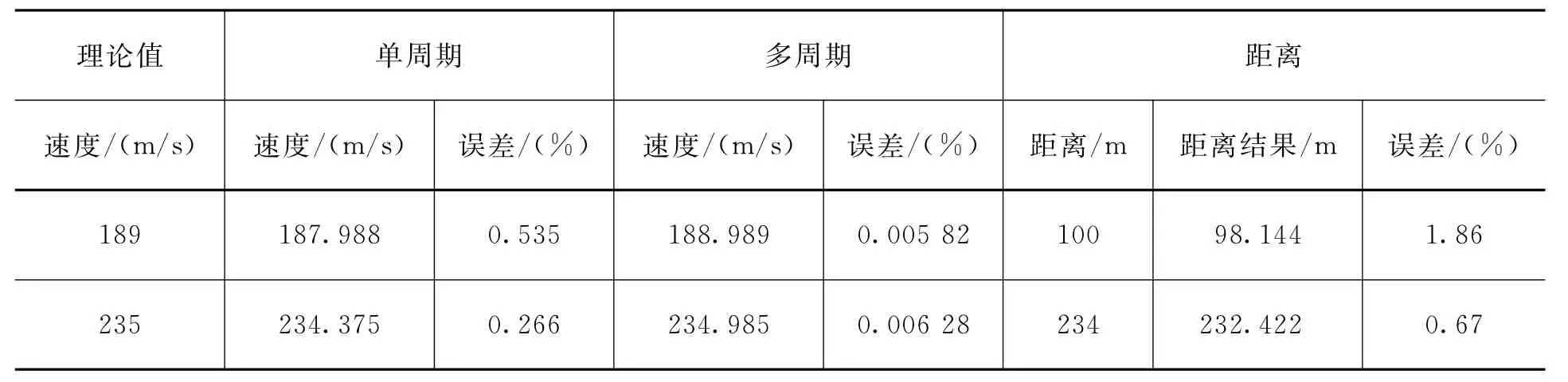
表4 两个速度不同，距离不同的目标的仿真数据

由表4可以看出，在提高了步进频个数M后，相比较于表3，距离误差有了明显的减小，由原来的平均误差2.7%下降到1.265%。对比表2，速度误差相比较原来的改进多周期速度误差有明显的减小。可见在提高M后能同时改善速度和距离测量精度。

4 结束语

本文分析了步进频连续波雷达多目标检测算法的原理，该算法结合了二维FFT算法，通过对N个FFT回波的速度通道峰值进行IFFT处理，从而达到多目标识别。针对单周期速度测量带来的速度分辨率较低的问题，提出了基于二维FFT算法的多周期速度改进算法，该算法能够有效改善速度分辨率。由于采用了多个周期的步进频连续波，所以需要进行的计算量较大，但经过仿真证明是有效可行的。