田口方法汽车平顺性分析与稳健优化

胡启国，杨晨光

(重庆交通大学 机电与车辆工程学院，重庆 400074)

汽车的平顺性主要是保证汽车在行驶过程中产生的振动和冲击环境对乘员舒适性的影响在一定界限之内[1]。悬架是影响汽车平顺性的主要因素，众多专家学者从事悬架系统的研究、优化与控制工作，使汽车平顺性得到不断地提高。文献[2]考虑了簧上质量变化、执行机构延迟等因素，设计了一个可靠的模糊H∞控制器，并采用四分之一车辆悬架模型验证了设计方法的有效性。文献[3]应用改进的多目标遗传算法优化了某种油气悬架的参数。文献[4]结合蒙特卡罗方法和6σ稳健性优化技术，对悬架参数进行多目标稳健性优化，改善了设计变量在最优解附近波动而引起平顺性变差的状况。但是，这些优化都将路面、载荷和车速等因素视为不变的，没有考虑随机干扰因素对汽车平顺性的影响，因而不能保证汽车平顺性在复杂工况下的稳健性。文献[5]将试验设计、稳健性理论和田口鲁棒设计方法相结合，构造了汽车耐撞性的稳健性优化设计方法，在获得近似最优解的同时，较大幅度提高了产品的稳健性。

田口方法是一种聚焦于最小化过程变异或使产品、过程对环境变异最不敏感的实验设计方法。本文考虑悬架参数、座椅参数等可控设计变量和路面、载荷、车速等随机干扰因素对汽车平顺性的影响，将仿真分析与田口方法相结合，分析了各可控设计变量与随机干扰因素对平顺性的影响，并优选出最佳参数组合，提高了整车平顺性及其稳健性。

1 路面激励模型

车辆振动的输入路面不平度主要采用路面功率谱密度来描述其特性[6]。这里采用滤波白噪声法建立路面激励时域模型，其单轮路面激励q(t)的时域模型为[7]

式中：n∞为路面空间截止频率，n∞=0.011 m-1；u为汽车行驶速度；n0为参考空间频率，Gq(n0)为路面不平度的几何平均值；n0=0.1 m-1；ω(t)为均值为0的单位白噪声随机信号。

同侧前后车轮所受激励存在迟滞性，单轮辙激励模型为[8]

式中：α为与路面等级相关的路面常数；q1、q2分别为汽车同侧前、后车轮的路面激励；l为汽车前后轴的距离；Δ为前后车轮路面激励的输入延迟，Δ=l/u。

左右两侧车轮轨迹具有异辙相干性，假设左、右两侧轮辙的白噪声输入ξ分别为ξx、ξy，则两侧轮辙相干性方程为

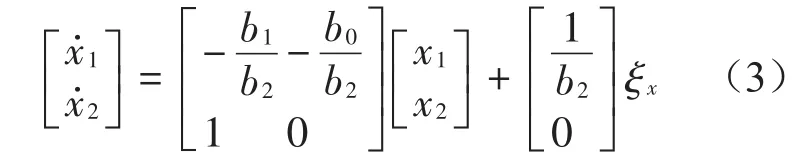
右侧轮辙白噪声输入模型为

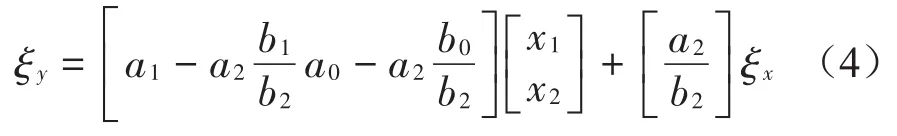
式中：a0、a1、a2、b0、b1、b2为道路品质常数，a0=3.181 5、a1=0.206 3、a2=0.010 8、b0=3.223、b1=0.59、b2=0.032 7；x1、x2为中间状态变量[9]。

本文所研究的汽车主要行驶在A级、B级和C级路面。对于A级、B级和C级路面，其路面不平度的几何平均值Gq(n0)和路面常数α的数值如表1所示。

以B级道路路面不平度作为车轮激励，取车速为u=20 m/s，在MATLAB/Simulink中进行仿真实验，得到汽车4轮所受路面随机激励如图1所示。

表1 路面参数Gq(n0)与α的取值

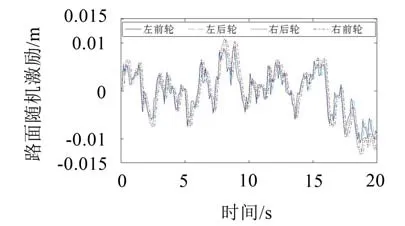
图1 汽车4轮所受B级路面随机激励

2 整车平顺性模型及仿真

2.1 动力学模型

经过合理简化，建立8自由度整车动力学模型如图2所示。该模型中，车身被简化为刚体，有质心的垂直位移（Zc）、侧倾角（Φ）和俯仰角（θ）3个自由度、驾驶员座椅垂直位移（Zs）1个自由度，4个非簧载质量分别具有1个垂直位移（Z1、Z2、Z3、Z4）自由度。

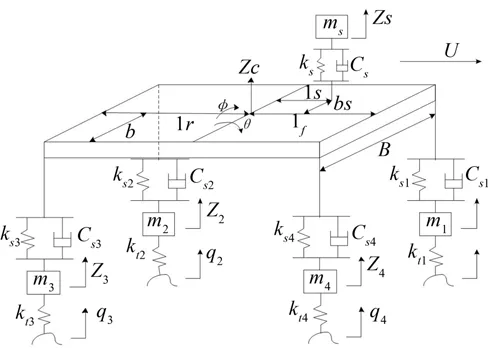
图2 整车8自由度振动动力学模型示意图

取系统的广义坐标为

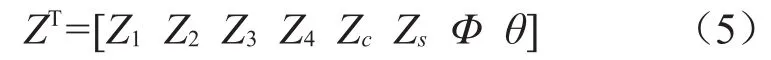
由拉格朗日方程和达朗贝尔原理，可得8自由度整车平顺性模型振动微分方程为

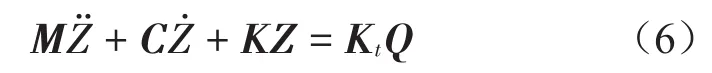
式中：M为8×8阶的系统质量矩阵；C为8×8阶的系统阻尼矩阵；K为8×8阶的系统刚度矩阵；Kt为8×4阶的轮胎刚度矩阵；Q为4×1阶的路面激励矩阵；Z为8×1阶的位移矩阵。

2.2 仿真分析

本文所研究汽车的动力学参数说明及取值见表2。

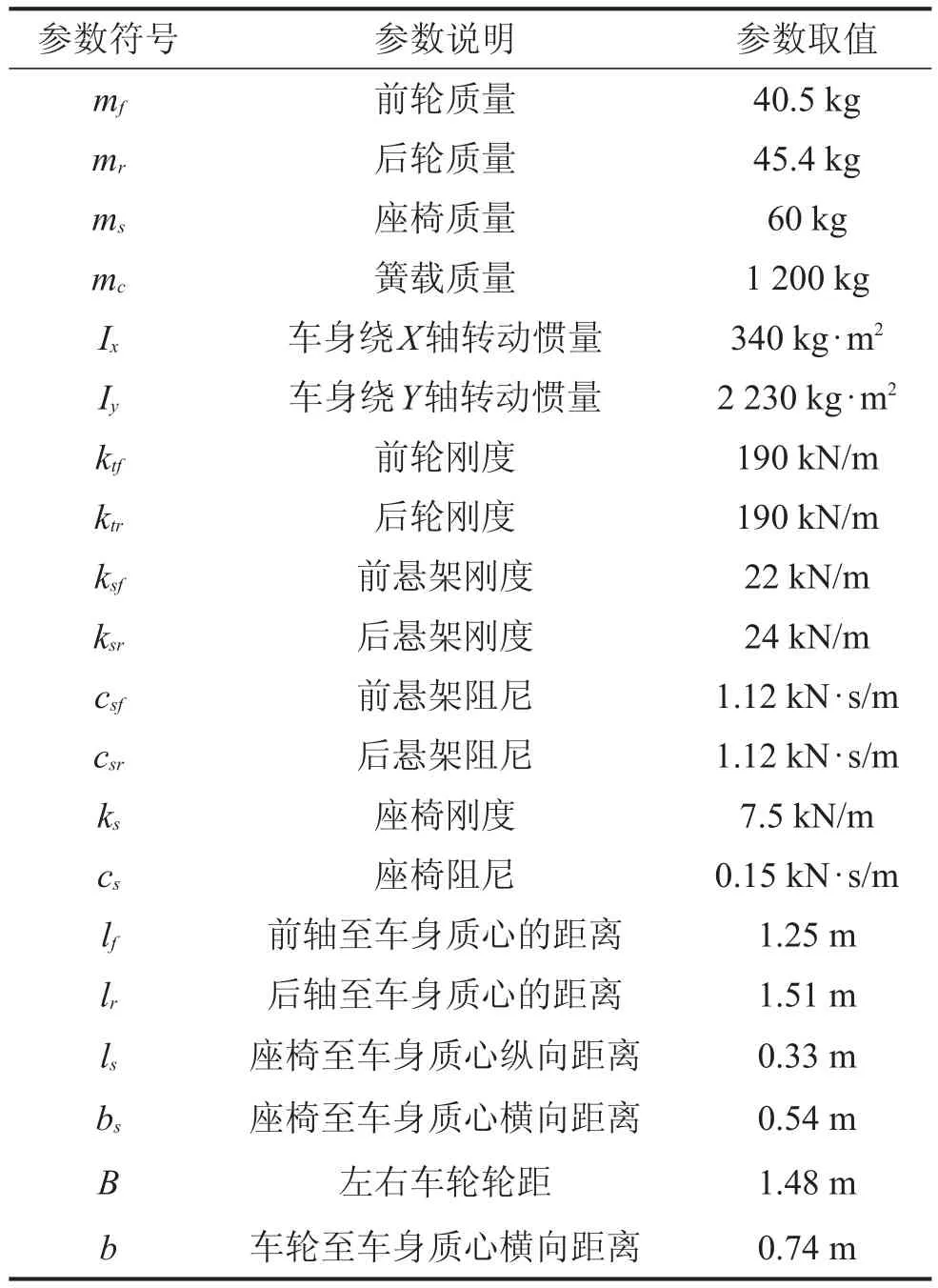
表2 汽车动力学参数说明及取值

利用MATLAB/Simulink进行仿真实验，模拟该车在C级路面、空载状况下以25 m/s的速度匀速行驶时的整车振动状况，得到驾驶员座椅垂向加速度随时间变化的曲线如图3所示。

图3 座椅垂向振动加速度图

在MATLAB中计算得到座椅垂向加速度均方根值为0.605 7 m/s2，根据文献[10]提供的垂向加速度均方根值与人主观感觉之间的关系可知，对于所研究车型，驾驶员的舒适性不够好，需要进行平顺性优化。

3 田口方法实验及稳健优化

田口方法实验是基于损失模型的稳健优化设计实验，其原理是利用设计参数和响应之间的非线性关系来实现产品的稳健性，其目的是寻找可控因素的最佳组合，使得噪声因素的影响尽可能小。田口方法的基本工具是信噪比和正交表；正交实验设计方法只需要做少数试验就能全面反映出试验条件完全组合的内在规律，以确定参数的最佳组合，可以缩短设计时间，提高设计效率[11]。

3.1 内外正交表的设计

悬架及座椅的动力学参数对汽车乘坐舒适性的影响较为明显。因此，这里选取前后悬架的刚度、阻尼和驾驶员座椅的刚度、阻尼作为6个可控因子。

该车型前悬架偏频范围为1.00 Hz～1.45 Hz，后悬架偏频范围为1.17 Hz～1.58 Hz。结合已知参数，可以计算出悬架参数的取值范围。为了详细分析可控因子各水平的影响，每个因子均选择5种水平，如表3所示。其中，水平3指该车初始设计参数值，其余水平对应的值分别为初始值的倍数。根据可控因子个数及其水平数，选取L25（56）正交表为内表。

表3 可控因子水平表

依据汽车平顺性的外界影响因素分析，选取路面等级、载荷和车速为3个噪声因子，其水平的选择根据该车型的常态行驶环境来确定，如表4所示。根据噪声因子的个数及其水平数，选取L9（33）正交表为外表。

表4 噪声因子水平表

3.2 信噪比

汽车平顺性的客观评价常以座椅的垂向加速度均方根值作为指标。这里以悬架动挠度和轮胎动载荷为约束条件，以驾驶员座椅的垂向加速度均方根值最小为优化目标，其值越小，汽车平顺性越好。

田口稳健设计要求目标函数及其在噪声因素干扰下的波动值越小越好。考虑望小特性，基于损失函数法的信噪比为[12]

式中：yi为对应的目标函数响应值。

3.3 实验结果分析

田口方法中，内正交表是可控因子各水平组合的安排，外正交表是噪声因子各水平组合的安排，由内外正交表的设计得到正交表的表头。在MATLAB/Simulink中对各种可控因子与噪声因子的组合依次进行仿真实验，得到座椅垂向振动加速度图，编程算出座椅垂向加速度均方根值（单位：mm/s2），并计算各可控因子组合下的响应均值和信噪比，得到实验结果如表5所示。

对表5的数据进行统计学分析与计算，得到信噪比的方差分析表，如表6所示。通过贡献率的计算，可以得出各可控因子对平顺性及其稳健性的影响程度。

由表6可知：各可控因子中，前悬架刚度对该车平顺性及其稳健性的贡献率最高，达到71.11%；后悬架刚度次之，为10.26%；前、后悬架的阻尼和座椅的刚度、阻尼对应的贡献率较小。因此，对于该车型，悬架的刚度对汽车平顺性影响显著，其设计与加工精度应着重考虑。

噪声因子的影响趋势如表7所示。由表7可知：汽车平顺性随路面不平度的增加而变差，随载荷的增加而改善，随速度的加快而变差。各噪声因子对汽车平顺性的影响程度由高到低依次为：路面、车速、载荷。

3.4 优化结果分析

稳健优化前后各可控因子的水平值及汽车在以上9种工况下的座椅垂向加速度均方根值（单位：mm/s2）如表8所示。由表8可知：优化后，汽车驾驶员座椅的垂向加速度均方根值在以上9种噪声因子的组合工况下均有所减小，其变化范围和均值均变小，其中，均值由345.1下降至267.9，减小了22.37%；信噪比变大；说明驾驶员座椅的舒适性显著提升，且其随噪声因子变化的波动范围变小，即提高了汽车的平顺性及其稳健性。

表5 田口方法实验正交表

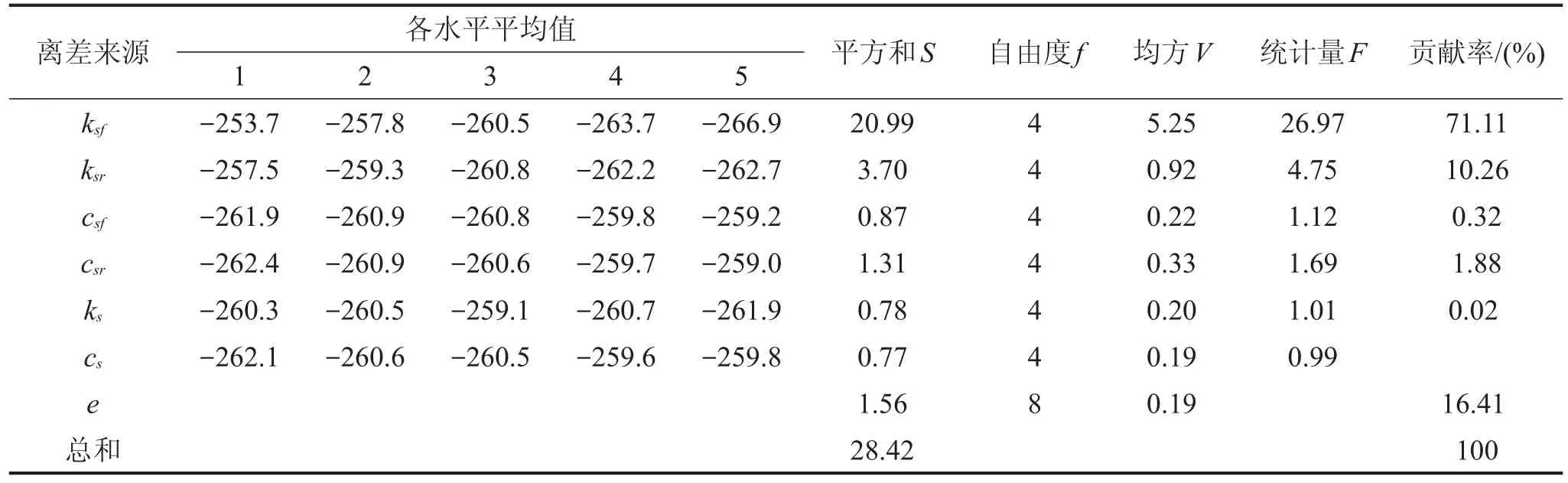
表6 信噪比方差分析表

表7 噪声因子反应表 单位：mm/s2

仿真实验结果显示：汽车各轮胎相对动载荷与各悬架动行程于优化前后的反应具有一致性。在以上9种工况下，右后轮相对动载荷均方根值gi与右后悬架动行程均方根值fi（单位：mm）如表9所示。

由表9可知：优化后，右后悬架动行程均方根值与右后轮相对动载荷均方根值在各工况下均减小，汽车操纵稳定性提升。信噪比增大，说明悬架动行程与轮胎相对动载荷在各工况下的波动范围也变小，汽车操纵稳定性的稳健性也有所提高。由此，验证了田口方法汽车平顺性分析与稳健优化的可行性。

表8 优化前后可控因子水平及响应分析

表9 优化前后汽车操纵稳定性分析

4 结语

（1）建立了8自由度整车平顺性模型，利用MATLAB/Simulink进行仿真实验，分析驾驶员座椅的乘坐舒适性，指出了所研究汽车平顺性的不足。

（2）通过田口方法试验，分析了汽车动力学参数变化与外界随机不可控因素对汽车平顺性的影响；优选出了汽车动力学参数的最佳水平组合，提高了汽车的操纵稳定性、平顺性及其稳健性。

（3）分析了悬架和座椅的动力学参数对汽车舒适性的影响和贡献率，为汽车的设计与生产标准提供了理论依据。本文的研究方法对汽车的振动、噪声等其它方面的研究具有一定的借鉴意义。