某中型履带式挖掘机越障动力学建模与分析
2018-02-20秦仙蓉赵书振沈健花孙远韬
秦仙蓉,赵书振,沈健花,张 氢,孙远韬
(1.同济大学 机械与能源工程学院,上海 201804;2.惠普信息技术研发有限公司,上海 200131)
由于工作性质的特点,履带式挖掘机工作环境十分恶劣,经常需要跨越石块、壕沟等障碍路面,而挖掘机的燃料箱等薄壁构件,在履带式挖掘机越障过程中受到来自地面的振动冲击,极易产生疲劳破坏,因此研究履带式挖掘机的整机越障动力学特性十分必要。
近年来,国内外学者对履带式挖掘机的研究主要有:履带式挖掘机底盘系统的动力学分析,履带式挖掘机的动力匹配及分析,履带式挖掘机的工作装置优化设计及可靠性分析等[1-5]。然而国内外针对履带式挖掘机越障特性方面的研究还较为少见,有关越障特性的研究主要集中在履带式移动机器人和高速履带车辆(即履带式装甲车辆)。相应的研究主要集中于两个方向:其一是研究对象为履带式移动机器人,通过理论分析其越障时的性能和稳定性等特征,研究现有机构的优缺点并进行优化设计;其二是以履带式装甲车辆为研究对象,结合多刚体运动学和动力学分析,研究履带式车辆在越障过程中的振动特性。
随着计算机技术的飞速发展,虚拟样机技术不断进步,给履带式车辆的研究提供了有效的研究手段。国内运用虚拟样机技术进行挖掘机的仿真分析主要还是集中于工作装置性能研究、最大挖掘机力、复杂作业工况的仿真以及机电液联合仿真分析方面[6-8],而关于履带式挖掘机越障工况的仿真分析的文献并不多见。
本文根据机械振动理论,以履带式挖掘机为研究对象,建立挖掘机越障过程中的简化力学模型和对应的数学模型,求解挖掘机越障过程中的动力学响应。建立某型履带式挖掘机的整机虚拟样机,实现多刚体动力学仿真,并与简化力学模型数值求解结果进行对比。
1 简化力学建模
考虑到履带式挖掘机承载型底盘系统的特点,并借鉴国内外学者的研究,建立履带式挖掘机的11自由度简化力学模型,分别为车体的垂向位移、车体的俯仰角、与驱动轮接触的履带节单元垂向位移、7个与支重轮接触的履带节单元垂向位移和与导向轮接触的履带节单元垂向位移,如图1所示。
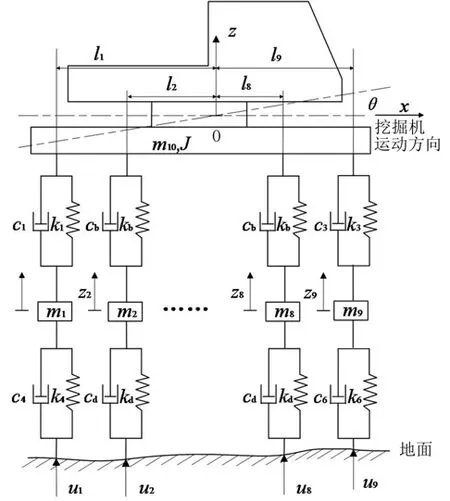
图1 履带式挖掘机简化力学模型
本力学模型不考虑履带式挖掘机的侧倾,即将问题简化为二维问题。力学模型的坐标原点置于整机的质心位置,x轴的正方向为车体前进方向,z轴的正方向为垂直向上方向,符合右手坐标系原则。某中型履带式挖掘机的单侧履带是由1个驱动轮、1个引导轮、7个支重轮、2个托链轮和1条履带组成。考虑到整机在行走过程的托链轮对于地面缓冲能力明显弱于其他轮子,且承载型底盘对地面缓冲作用主要是驱动轮、支重轮和引导轮通过履带与地面接触来实现,因此不考虑托链轮,除了车体的质量块m10外分9个模块,分别表示1个驱动轮、7个支重轮和1个引导轮与履带板以及对应履带板与地面之间的接触作用。
图1所示的力学模型中,m10表示车体质量;J表示车体转动惯量;l1表示驱动轮到质心的距离;li(i=2,…,8)表示各支重轮到质心O的距离;l9表示引导轮到质心的距离;mi(i=1,…,9)表示与各轮接触的履带节单元的等效质量;k1、kb、k3分别表示驱动轮、支重轮与导向轮和履带接触的换算刚度,c1、cb、c3分别表示驱动轮、支重轮与导向轮和履带接触的换算阻尼,这里认为7个支重轮与履带接触的换算刚度(图中都以kb表示)、换算阻尼相同(图中都以cb表示);k4、kd、k6和c4、cd、c6分别表示驱动轮、支重轮、导向轮下履带节单元与地面接触的换算刚度和换算阻尼,这里认为7个支重轮下履带节单元与路面接触的换算刚度(图中都以kd表示)、换算阻尼(图中都以cd表示)相同;ui(i=1,…,9)表示各轮下的路面激励。
11自由度的广义坐标为
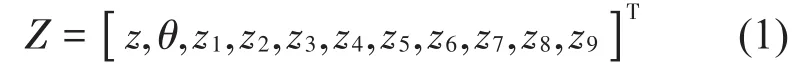
其中:z表示车体的垂向位移,θ表示车体的俯仰角(逆时针为正),zi(i=1,…,)表示各等效质量的垂向位移。
建立简化力学模型之后,由拉格朗日法可求得系统的运动微分方程为
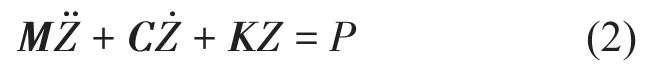
其中,质量矩阵为
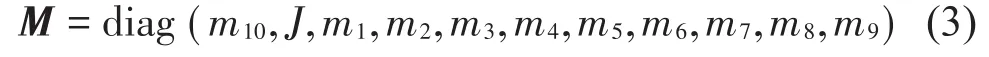
系统刚度矩阵为
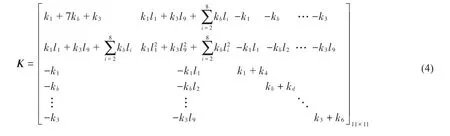
系统阻尼矩阵为
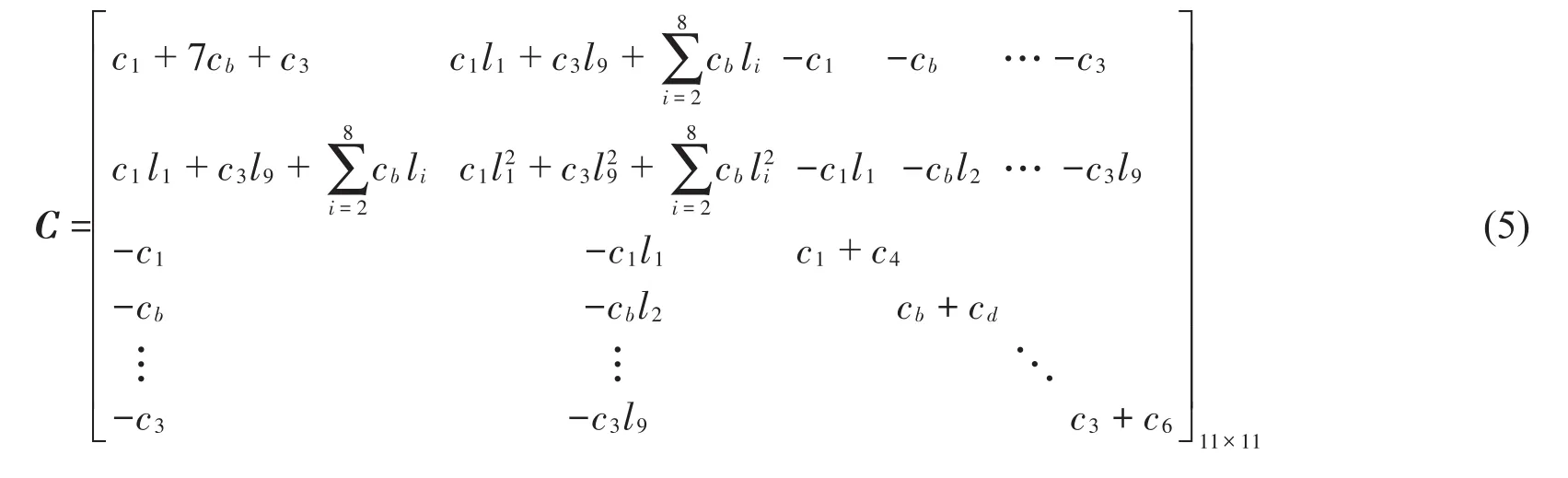
系统的广义力矩阵为

综上,建立了履带式挖掘机的简化力学模型以及相应的数学模型。
2 某中型履带式挖掘机越障动力学分析
2.1 路面激励参数确定
参考GB7031-1986《车辆振动输入路面不平度表示方法》,本文采用的路面输入形式有两类:其一是垂直障碍物,其二是路面不平度。
2.1.1 路面障碍激励
路面垂直障碍如图2所示,障碍物的参数为高度h和长度l。对于某中型履带式挖掘机,障碍物高度h设置为其极限越障高度h=0.267 m,设定长度l=0.5 m。
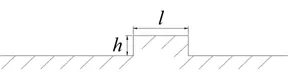
图2 路面障碍激励形式
由于履带环将驱动轮、支重轮和引导轮围成一个整体,当挖掘机某一轮子攀爬到障碍物边缘时,其余各轮下的路面障碍参数h必大于等于0,因此该简化力学模型的路面障碍激励需要考虑履带作用。主要分3个阶段分析该型履带式挖掘机越障过程中的路面障碍激励:挖掘机爬上障碍物、在障碍物上行驶和驶下障碍物。
履带式挖掘机的行驶速度分为两档:高速挡约0~1.53 m/s和低速挡约0~0.97 m/s,本模型研究的是履带式挖掘机越障动态响应,行驶速度设为低速挡的最大值,约0.97 m/s。以自由度z5为例,在该自由度上,路面障碍激励如图3所示。
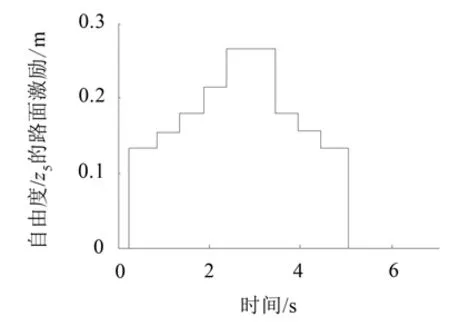
图3 自由度z5的路面障碍激励
2.1.2 路面不平度激励
履带式挖掘机在不平路面上行驶,使得各轮不断受到路面障碍冲击,产生较大的惯性力,进而造成挖掘机上薄弱环节的早期疲劳损坏,因此,在振动分析中考虑路面不平度的影响很有必要。大量的试验测试表明:路面不平度是具有零均值、各态历经的高斯随机过程。国标GB7031-1986根据路面功率谱密度把路面不平度分为8级,据大量统计数据分析,履带车辆经常作业的田野地面相当于F级路面,履带车辆碾压损坏的路面相当于G级,因此本文将模拟这两种路面激励。
根据国标中给出的路面不平度功率谱密度拟合公式,推导出路面不平度的理论计算公式,进而求出各轮的路面不平度激励。
在后面的瞬态响应分析中,分两种情况模拟路面激励:
(1)如图3所示,各自由度上只有路面障碍激励;
(2)同时考虑两种类型路面激励,即将路面障碍激励与路面不平度激励叠加。仍以自由度z5为例,在该自由度上叠加后的路面激励如图4所示。
2.2 质量、刚度和阻尼参数确定
通过查找相关资料,结合三维实体模型,确定各部分的质量参数如表1所示。
学者Nakanishi.T和Shabana.A.A[9-10]对日本小松公司的PC120型履带式挖掘机的各轮与履带板以及履带板与路面间的换算刚度和换算阻尼研究较为深入。考虑到履带式挖掘机行走原理的相同性,本文中驱动轮、支重轮和引导轮与履带板以及履带板与地面之间的换算刚度和换算阻尼均参考文献[10]中的换算刚度和阻尼,如表2所示。
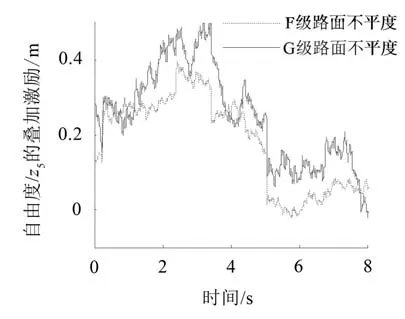
图4 自由度z5上路面障碍与不平度激励叠加

表1 挖掘机力学模型质量参数

表2 力学模型中换算刚度和换算阻尼取值
为了后续模型响应的计算,还需确定各轮与质心之间的距离l1~l9。根据建立的三维实体模型确定这些尺寸参数的值{l1,l2,,… ,l9}={-2.087,-1.502,-1.017,-0.502,0.012,0.527,1.042,1.527,2.118},单位为m。
2.3 动力学响应求解
根据所建立的动力学模型,运用状态空间法建立系统的状态方程,借助MATLAB,计算给定激励下系统的动力学响应。
2.3.1 仅路面障碍激励下的瞬态响应
仅考虑路面障碍参数作为激励,求解得到车体质心垂向位移响应和垂向速度响应如图5和图6所示。
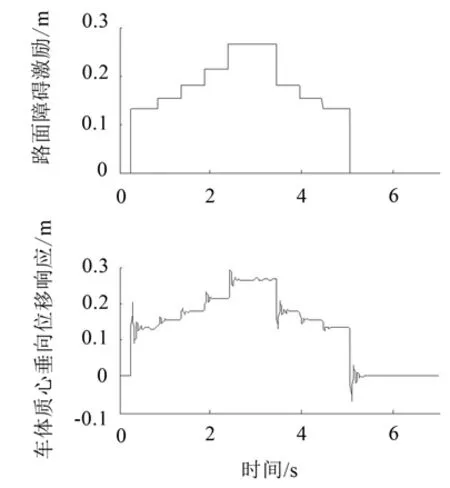
图5 路面障碍激励与车体质心垂向位移响应
如图5所示,车体质心垂向位移响应与自由度z5上路面障碍激励几乎是吻合的,因为车体质心离z5的水平距离为0.012 m,几乎在同一个垂线上。车体质心垂向位移响应可以看作是力学模型对一系列阶跃激励的响应,每一个阶跃激励表示车体的一个轮子爬上或爬下障碍物,共计9个阶跃激励。在2.5 s~3.5 s内车体垂向位移响应最大,最大值约0.31 m,均值约0.27 m,与预设的障碍高度0.267 m接近。
图6为车体质心垂向速度响应,可以看出,车体每经历一个路面输入阶跃激励作用,车体的垂向速度会有较大幅度的波动,最大的速度幅值约为8m/s。结果符合理论分析和预期,能比较真实地反映实际履带式挖掘机的越障动态响应,说明简化力学模型较准确。
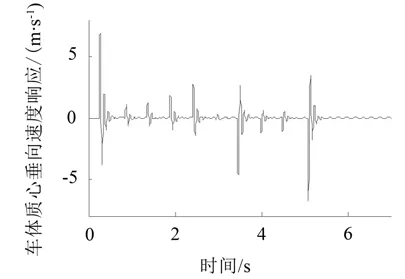
图6 仅路面障碍激励下车体质心垂向速度响应
2.3.2 路面障碍与路面不平度同时激励下的瞬态响应
文中讨论的路面不平度激励级别为F级和G级,考虑路面障碍激励和路面不平度两种类型激励的叠加,求解得到车体质心垂向位移响应和垂向速度响应如图7。
如图7所示,在G级路面不平度激励下的车体质心垂向位移响应要大于在F级路面不平度激励下的响应。
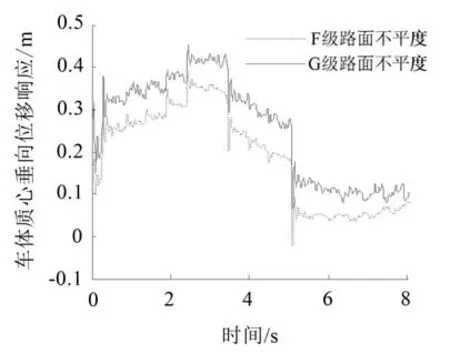
图7 路面障碍与路面不平度同时激励下的车体质心垂向位移响应
对比图5和图7可明显发现,当路面障碍叠加路面不平度作为激励时,车体质心垂向位移明显增大,叠加F级路面不平度作激励时,最大车体质心垂向位移响应约0.4 m;叠加G级路面不平度作激励时,最大车体质心垂向位移响应约0.47 m
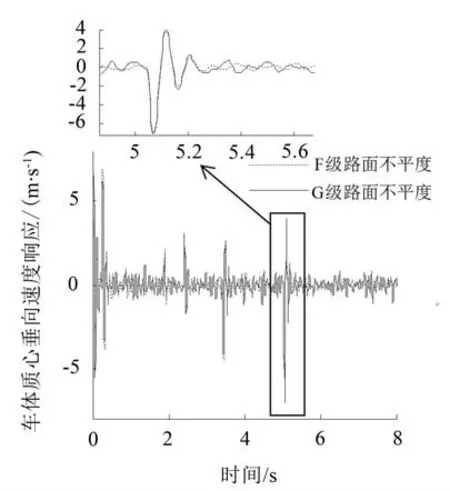
图8 路面障碍与路面不平度同时激励下的车体质心垂向速度响应
由图8可得,在G级路面不平度激励下,车体质心垂向速度响应幅值比F级路面不平度激励下的响应要大,结果符合理论分析和预期。
3 履带式挖掘机越障动力学仿真
通过建立前文所述履带式挖掘机的虚拟样机模型,进行越障动力学仿真,将动力学仿真结果与前文所得数值分析结果对比,对两个模型进行相互校验。
采用三维建模软件建立履带式挖掘机的实体模型,将其导入ADAMS。为减小计算量,对模型做相应简化:只建立单侧履带;将工作装置省去并根据其重力在履带的行走架上添加相应的力;忽略一些次要零件比如销套、螺栓螺母等。添加约束,定义各零件之间的运动关系:驱动轮、7个支重轮、导向轮与2个托链轮和行车架用旋转副连接;55个履带节单元之间用旋转副连接;车体和行车架之间添加固定副。添加驱动:以转动角速度的形式施加到驱动轮上,使模型能达到与前面相同的前进运动状态。建立的虚拟样机模型如图9所示。

图9 ADAMS虚拟样机模型
ADAMS中接触有两大类:瞬时接触和连续接触。瞬时接触使用的是弹簧阻尼模型,而连续接触采用的是非线性弹簧模型。本研究课题中履带节单元与各轮子和地面之间的接触属于瞬时接触,因为在每一时刻只有特定数量的履带节单元与各轮子和地面接触。所有零件之间的接触均采用impact接触力来实现,采用ADAMS自带的宏命令Macros功能,编写cmd程序,实现近700对接触力的自动添加。
在ADAMS中进行参数设置,如表3所示。刚度是接触的刚度;作用因子是计算瞬时法向力时刚度的贡献值指数,对于金属通常取1.3~1.5;阻尼是指接触的阻尼属性,一般取为刚度值的0.1%~1%。选定接触摩擦力为库伦摩擦形式时,还需要定义静摩擦系数、动摩擦系数、引起摩擦系数变化的速度临界值黏滞转换速度(由动摩擦转变为静摩擦)和摩擦转换速度(由静摩擦转变为动摩擦)等参数。
动力学仿真初始条件设置与简化力学模型计算条件相同,即驱动轮恒定转速为125 deg/s(2.18 rad/s),使样机前进速度达到0.97 m/s。外部激励选为相同的路面垂直障碍物激励,障碍物高度为0.267 m,宽度为0.5 m,仿真总时长为6.5 s,仿真步数为2 000步。
将ADAMS虚拟样机仿真所得的车体质心垂向位移响应与简化力学建模所得的结果对比,结果如图10所示。
由图10可知,在初始条件设置相同时,虚拟样机仿真所得结果与简化力学建模所得结果趋势一致,简化力学建模所得的车体质心垂向位移响应最大值约为0.31 m,在6 s之后车体质心垂向位移响应趋于平稳;虚拟样机仿真所得的车体质心垂向位移响应最大值约为0.28 m,约6.1 s后曲线趋于平稳,越障过程结束。以车体质心垂向位移响应为例,说明了两种动力学建模及分析方法具有可比性,可以相互校验。
虽然两种分析方法所得的结果趋势一致,但在响应速度上有一定差异,主要原因是模型建立方法的差别和参数设置的不同。简化力学模型刚性更强。
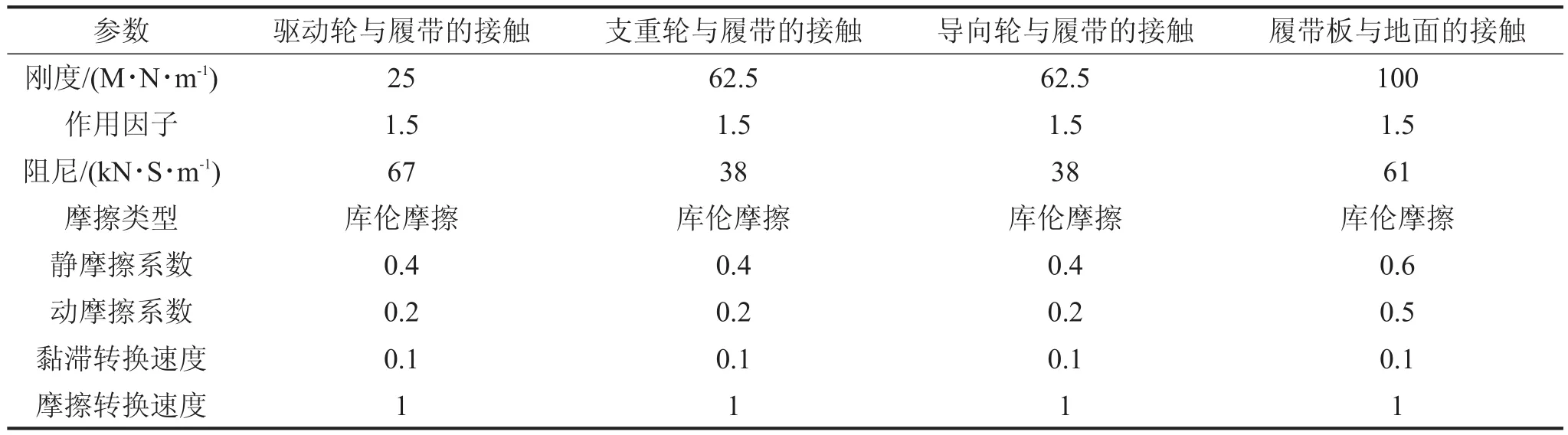
表3 虚拟样机模型接触参数设置
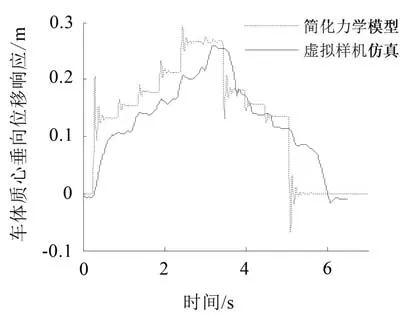
图10 两种模型车体质心垂向位移响应对比
4 结语
以某中型履带式挖掘机为工程实例,建立了履带式挖掘机越障过程的简化力学模型和对应的数学模型,求解了其越障过程的动力学响应。同时,建立该履带式挖掘机的整机虚拟样机,实现多刚体动力学仿真。
在只有路面越障参数激励下,根据所建立的简化力学模型求得的车体质心垂向位移响应的均值约0.27 m,与预设的障碍高度0.267 m接近,符合理论分析和结果预测。
考虑路面不平度与路面障碍共同激励时,简化力学模型在G级路面不平度和路面共同激励、F级路面不平度和路面垂直障碍共同激励两种情况下,车体质心垂向位移及速度响应幅值符合理论分析和预期,说明所建模型可以达到挖掘机非作业状态动态特性研究的要求。
在只有路面垂直障碍物激励时,以虚拟样机模型为系统,通过仿真,将得到的结果与简化力学模型的结果对比,发现车体垂向位移响应趋势基本一致,实现了两种动力学模型的相互校验,说明了所提出的动力学建模与分析方法的正确性,可为履带式挖掘机越障动态特性研究提供借鉴与参考。
