部分可观测车辆系统非线性随机振动的最优控制

张 巍，应祖光，颜光锋

（1.浙江理工大学 经济管理学院实验中心，杭州 310018；2.浙江大学 航空航天学院力学系，杭州 310027）

车辆运行过程的振动水平是评估其动力学性能的重要指标，该振动对于车载器件的正常工作具有极其重要的影响，因此必需进行车辆振动控制。由于路面不平度的随机性，车辆振动是随机的，需要进行随机振动控制。通常车辆由车轮、轴等垂直支承，系统一般是线性的。这类车辆的被动、主动与半主动控制已有很多研究[1-6]。然而，一类特殊的重型多轴车辆受空间限制其悬架采用可转动的斜杆支承，从而导致系统的几何非线性[7]，其非线性随机振动控制方法与效果完全不同于普通车辆。对于反馈控制，还需要考虑状态观测，由于观测噪声不可避免，故不能由测量值直接确定系统状态，导致出现不完全观测或部分观测的控制问题[8]。部分可观系统的非线性随机最优控制是一个极其困难的问题，研究成果非常有限，例如文献[9]在十分特殊的条件下给出一个控制策略，先将部分可观系统的非线性随机最优控制问题转化为完全可观线性系统的随机最优控制问题，再根据随机动态规划原理确定控制律。最近文献[10-11]发展了基于推广的Kalman滤波的非线性随机最优控制策略，可用于一般的部分可观系统的非线性随机最优控制，从而为斜杆支承车辆系统的振动控制提供了一个基本策略。

关于可转动斜杆支承车辆系统振动控制的研究非常有限，例如文献[7]通过多体动力学分析讨论了斜杆支承悬架的优化，因此需要进一步深入研究。实际上，在悬架与车轮间安装控制器，产生一对作用力是通常的措施，但受空间限制也只能类似于支承的斜向安装。控制器一般采用磁流变阻尼器[12]，从而导致一个半主动控制问题。控制器的作用力是有限的，它将成为一个控制约束[13-14]。且控制目标是车体相对于不平路基准面的绝对振动水平，不同于通常关于结构强度的振动控制。总之，该部分可观斜杆支承车辆系统的非线性随机最优控制是一个新的有待于研究的重要问题。

本文研究上述具有观测噪声的斜杆支承与控制的非线性车辆系统，在随机路激励下振动的部分可观非线性随机最优有界控制新问题，考虑车体与车轮的垂直耦合运动及斜支承杆的转动，用拉格朗日方程建立车辆控制系统模型的运动微分方程，再转化为非线性的耦合振动方程，同时建立包含测量噪声的系统观测方程，组成部分可观系统的非线性随机最优控制问题；根据推广的Kalman滤波方法得到关于估计状态的非线性随机系统方程，再根据随机动态规划原理建立动态规划方程，考虑控制力的有界性约束，得到基于系统估计状态的最优有界控制律；最后，比较受控与未控系统的响应统计评估控制效果，通过数值结果说明不同观测系数下本文方法的有效控制结果。

1 随机路激励非线性车辆系统振动控制的基本方程

可转动斜杆支承与控制的车辆系统简化模型如图1所示。

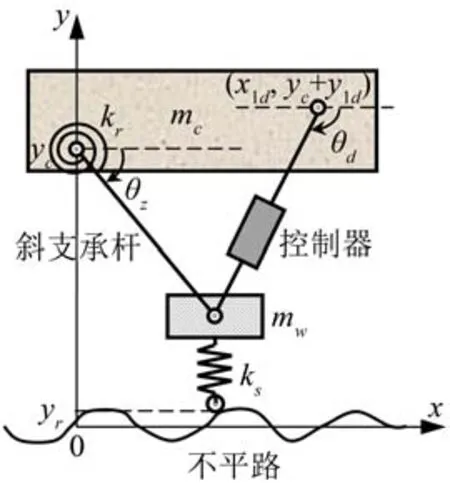
图1 斜杆支承与控制的车辆系统模型简图

车体质量为mc，车轮质量为mw，车体由可转动的斜杆支承，控制器如磁流变阻尼器也斜向装于其间。车体主要运动为垂直方向，用绝对坐标yc描述。斜支承杆长度为lz，其转动用转角θz描述。车轮产生水平与垂直运动，可通过yc与θz表示。斜杆的扭转刚度为kr，预设角度为θz0。车轮的支承弹簧刚度为ks，弹簧原长为rw0。控制器上端的坐标为(x1d，yc+y1d)，由几何关系可确定其转角θd与两端距离ld。x轴表示路面基准线，路面不平度用yr(x)描述，当车辆前进速度为v时，受到的激励为yr(vt)，它通常是随机过程。

由第二类拉格朗日方程得到车辆系统的动力学方程

式中：g是重力加速度，Fd是控制器的作用力。对于磁流变阻尼器，根据Bingham模型，控制力为

式中：C0是黏性阻尼系数，fy是屈服力，U是半主动控制力，对于确定的阻尼器其值是有界的。

由几何关系得阻尼器两端距离与角度

由方程式(1)至式(2)确定相应的静平衡关系，利用此关系与式(3)至式(5)，将方程式(1)至式(2)化为振动方程

式中线位移u=yc-y0，角位移α=θz0-θ0，y0与θ0是静平衡时的线坐标和角坐标，由静平衡关系确定。由方程式(6)至式(7)可见，该车辆系统具有强几何非线性，并受随机路激励。

设系统的观测量为速度u˙与α˙，其中将包含测量噪声，因此不能由测量值直接确定速度，故称为不完全观测或部分观测。它可表示为

式中：φ1与φ2是观测量，d1与d2是放大系数，Ws1与Ws2是独立的单位强度观测噪声，e11与e12表示其幅值。方程式(6)至式(9)构成一个部分可观非线性随机振动的控制问题。

设系统状态向量Z=[u,α,˙,˙]T，观测向量Φs=[φ1,φ2]T，则系统方程与观测方程可表示成矩阵形式

式中向量A、B、F由方程式(6)至式(7)确定，矩阵D与E由方程式(8)至式(9)确定，W是单位强度白噪声，Ws=[Ws1，Ws2]T。W由随机路激励yr确定，对于一般不平路面，yr可通过滤波白噪声模拟，其方程为式中空间截止频率n00=0.01 m-1，参考空间频率n0=0.1 m-1，Gq是路面功率谱密度，描述路面不平度，按其不同值区分路面等级。此时，通过扩展状态向量Z，系统方程仍可表示为式(10)。

2 基于推广Kalman滤波的随机最优有界控制律

部分可观非线性随机控制问题表达式(10)至式(11)包括最优状态估计与基于估计状态的最优控制。最优估计的性能指标为

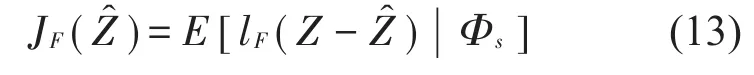
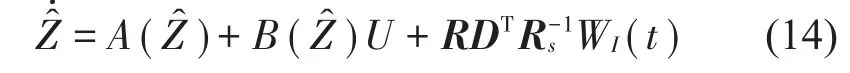
式中：WI是高斯白噪声向量，方差矩阵Rs=EET，估计偏差的方差矩阵R由下列方程确定

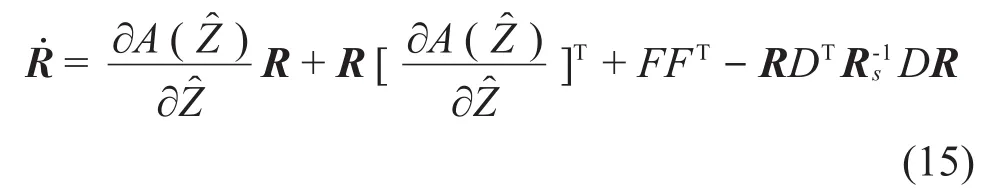
因R较快趋向于平稳，故可取方程式(15)的平稳解。

系统表达式(14)最优有界控制的性能指标为

式中：函数fC(Z)≥0，tf是控制的终时，ψ是控制终值。根据随机动态规划原理可得非线性随机系统表达式(14)与指标式(16)的动态规划方程[10-11]

式中：V是值函数，tr[⋅]是迹算符。考虑控制力U的有界性，通常有U∈[-Ua,，Ua]，Ua为控制力界限。由式(17)左边第二项极小化可得最优有界控制律

对于半主动控制，最优控制律还需满足式(3)。如果不满足时，只能取为0，因此控制效果有所影响。将式(18)代入式(17)得到值函数方程，求解之得到V，通常可取平稳解，从而由式(18)确定最优控制。再由方程式(14)计算估计系统响应，结合估计偏差的方差可计算原系统的响应统计。比较受控与未控系统的响应可评估控制效果。

3 数值结果

考虑具有观测噪声的受随机路激励的斜杆支承与控制的车辆系统模型，其基本参数为：mc=2 804 kg，mw=104 kg，lz=0.33 m，kr=13 kN⋅m/rad，ks=2×107N/m，θz0=0.96 rad，rw0=0.295 m，x1d=0.621 m，y1d=0.312 m，C0=1 640 kg/s，e11=0.03，e12=0.03，d1=1，d2=1，Ua=2.5 kN，车速v=50 km/h，B级不平路。按照上述方法确定最优控制，用龙格-库塔法计算系统响应，再作统计，数值结果如图2至图6所示。图2为车辆在B级不平路面以50 km/h前进时路面相对基准线波动位移随时间变化的曲线，表达了随机路激励。

图2 车速50 km/h工况下的不平路面

图3展示了半主动控制、主动控制与未控制时车体振动位移响应随时间的变化，其中主动控制是按式(18)确定的最优控制，半主动控制是按式(18)确定最优控制并满足阻尼器动力学约束式(3)。未控制时车体位移标准差为0.047 3 m，半主动控制时的车体位移标准差为0.015 4 m(相对降低67%)，主动控制时的车体位移标准差为0.013 8 m(相对降低71%)。可见上述最优控制能显著降低车辆系统的非线性随机振动，主动控制效果略好于半主动控制，因为半主动控制受到一定约束。

图4展示了半主动控制、主动控制与未控制时车体振动速度响应随时间的变化，同样地主动控制与半主动控制均能显著降低车辆系统的非线性随机振动速度，因此能有效控制车体振动能量。

图5展示了半主动控制、主动控制与未控制时车体振动位移响应标准差随观测噪声幅度系数e11的变化，车体振动响应标准差随观测噪声幅度系数e12变化的情况类似。可见在一定范围内，不同观测噪声幅度系数或噪声强度对于半主动控制与主动控制时车体振动响应标准差的影响较小。

图3 车体振动位移响应

图4 车体振动速度响应

图5 车体振动位移响应标准差随观测噪声幅度系数e11变化

图6展示了半主动控制、主动控制与未控制时车体振动位移响应标准差随观测响应放大系数d1的变化，车体振动响应标准差随观测响应放大系数d2变化的情况类似。在较大范围内，不同观测响应放大系数对于半主动控制与主动控制时车体振动响应标准差的影响较小。因此上述部分可观的最优控制对于不同观测系数具有一定的鲁棒性，改善控制器以减少控制约束可进一步提高控制效果。

总之，上述部分可观的最优主动与半主动有界控制能显著降低斜杆支承车辆系统在随机路激励下的非线性随机振动，且该控制结果对于状态观测噪声强度与观测响应放大系数具有一定的鲁棒性。

图6 车体振动位移响应标准差随观测响应放大系数d1变化

4 结语

本文研究了具有观测噪声的斜杆支承车辆系统受随机路激励的非线性随机振动控制，发展了该部分可观车辆系统的非线性随机控制新策略。考虑车体与车轮的垂直耦合运动及斜支承杆的转动，建立了部分可观车辆控制系统模型的非线性随机振动方程与包含测量噪声的系统观测方程，建立了该部分可观车辆系统的非线性随机最优控制模型。根据推广的Kalman滤波方法得到了关于估计状态的非线性随机系统方程，从而将部分可观车辆系统的非线性随机最优控制问题转化为完全可观的非线性随机最优控制问题。根据随机动态规划原理建立了完全可观系统的动态规划方程，并结合控制力的有界性，得到了基于系统估计状态的最优有界控制律，实现了主动控制，同时对于磁流变阻尼器实现了相应的半主动控制。数值结果说明了该控制策略可有效地降低具有观测噪声的斜杆支承与控制车辆系统在随机路激励下的非线性随机振动，并对于不同观测系数具有一定的鲁棒性。