浅谈空间向量与立体几何
2018-02-19云南省文山州广南县第一中学
云南省文山州广南县第一中学 王 龙
高考对立体几何平行与垂直的考查是高考的热点和重点,可以考查线面垂直的判定与性质、面面垂直的判定与性质,也可以考查线面平行的判定与性质、面面平行的判定与性质,解题思路有几何法和向量法两种.对空间角的考查重点考查异面直线所成角、线面角、二面角,思路也有两种,几何法与坐标法,几何法运算量小,但辅助线不易做,坐标法思路明晰,但运算量大,容易出错。利用空间向量解决立体几何问题,考查空间向量能力和运算求解能力和转化与化归思想。
一、刻画直线与平面方向的向量
1.直线
用直线的方向向量刻画直线的方向问题,而方向向量可由直线上的两个点来确定。
2.平面
用平面的法向量来刻画平面的倾斜程度,何为法向量?与平面垂直的直线称为平面α的法线,法线的方向向量就是平面的法向量,如何求出指定平面的法向量呢?
(1)所需条件:平面上的两条相交的直线。
二、空间向量可解决的立体几何问题
1.判定类
2.计算类:
(2)线面角:
(3)二面角:
(4)点到平面距离:设A为平面α外一点,P为平面α上任意一点,则A到平面α的距离为即在法向量上投影的绝对值。
三、点的存在性问题
立体几何在高考解答题中,最后一问往往涉及点的存在性问题,即是否在某条线上存在一点,使之满足某个条件,主要介绍使用空间向量解决该问题时的方法与技巧。
解答此类题目,以2016全国卷Ⅲ,以第19题为例:
例1、如图,四棱锥P⊥ABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M线段AD上一点,AM=2MD,N为PC的中点.(I)证明MN∥平面PAB;(II)求直线AN与平面PMN所成角的正弦值。
试题分析:
试题解析:
(II)取BC的中点E,连结AE.由AB=AC得AE⊥BC,从而AE⊥AD,且以A为坐标原点,的方向为x轴正方向,建立如图所示的空间直角坐标系A-xyz.由题意知P(0,0,4),M(0,2,0),

设n=(x,y,z)为平面PMN的一个法向量,则即
可取n=(0,2,1).于是
考点:空间线面间的平行关系,空间向量法求线面角.
技巧点拨:
(1)证明立体几何中的平行关系,常常是通过线线平行来实现,而线线平行常常利用三角形的中位线、平行四边形与梯形的平行关系来推证。
(2)求解空间中的角和距离常常可通过建立空间直角坐标系,利用空间向量中的夹角与距离来处理。
四、向量法解决二面角问题
解答本此类题目,以2017全国卷Ⅲ,理19第二问为例:
例2、如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.

(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D-AE-C的余弦值.
试题解析:由题设及(1)知,OA,OB,OD两两垂直,以O为坐标原点,的方向为x轴正方向,为单位长,建立如图所示的空间直角坐标系O-xyz.则A( 1 , 0,0),B( 0,0),C( - 1,0,0),D(0 , 0,1).

设n=(x,y,z)是平面DAE的法向量,则
考点:二面角的平面角;二面角的向量求法
技巧点拔:
(1)求解本题要注意两点:一是两平面的法向量的夹角不一定是所求的二面角,二是利用方程思想进行向量运算时,要认真细心,准确计算。
五、量法解决立体几何探索性问题
解答本类题目,以2016北京,理17 第三问为例:
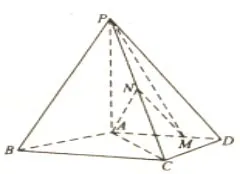
例3、如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=.

(I)求证:PD⊥平面PAB;
(II)求直线PB与平面PCD所成角的正弦值;
(III)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求的值;若不存在,说明理由.
试题解析:
(I)、略
(II)如图建立空间直角坐标系O-xyz,由题意得,A(0,1,0),B(1,1,0),C(2,0,0),D(0,-1,0),P(0,0,1)

考点:空间线面垂直的判定定理与性质定理;线面角的计算;空间想象能力,推理论证能力。
技巧点拔:
平面与平面垂直的性质定理的应用:当两个平面垂直时,常作的辅助线是在其中一个平面内作交线的垂线,把面面垂直转化为线面垂直,进而可以证明线线垂直(必要时可以通过平面几何的知识证明垂直关系),构造(寻找)二面角的平面角或得到点到面的距离等。
高考对本部分内容的考查以能力为主,重点考查空间想象能力,线面关系、面面关系、数形结合的思想等。
高考试题对该部分内容考查的主要角度有两种:一种是利用立体几何的知识证明线面关系、面面关系;一种是考查学生利用空间向量解决立体几何的能力.重点对该部分内容的考查仍将以能力考查为主,要求学生有良好的空间想象能力和立体几何素养。
