基于高阶有限元法的均匀流中物体二阶波辐射问题研究
2018-02-15王玉红王赤忠
刘 源,王玉红,王赤忠*
(1.陆军军事交通学院 镇江校区,镇江 212003) (2.浙江大学 海洋学院,舟山 316021)
波-流-体相互作用是船舶与海洋工程中最具挑战性的课题之一.流的存在会显著改变波浪参数,如波高、频率等.船舶和钻井平台等海洋结构物在波-流联合作用下,其受力和运动发生显著变化,甚至会导致结构物的破坏从而影响其安全性.因此,对波-流-体相互作用研究在海洋工程领域备受关注.
文献[1]中 基于时域线性理论,研究了位于均匀流中半圆柱的二维辐射和绕射问题,分析了均匀流对漂浮物体处的波浪爬高及作用在物体上的水动力的影响.随后,将此方法拓展到了三维垂直圆柱绕射问题[2].文献[3]中也作了类似的研究,研究表明:当入射波传播方向和水流方向相同时,上游处的波浪爬高会显著增大,同时水流对作用在结构物上的水动力载荷有明显的影响,特别是对二阶平均力的影响尤为显著.文献[4-5]中采用时域二阶理论,计算了三维垂直圆柱处的波浪爬高及其所受水动力.国内学者也作了类似的工作[6-7].目前完全非线性理论的波-流和结构物相互作用方法已经建立并得到应用[8-13].相比较线性或二阶理论而言,基于非线性理论的数值计算需要更多的计算资源.
以上波-流-体相互作用研究主要是关于绕射问题,而对于波-流-体辐射问题的研究则很少,主要工作基于线性理论,如文献[1].文中基于时域二阶理论,采用高阶有限元法研究均匀流中半圆柱的辐射问题,将文献[1]中的位于均匀流中的线性辐射问题扩展到二阶,计算自由表面波和半圆柱所受到的波浪力,分析水流对一、二阶波及作用在半圆柱上的一、二阶水动力的影响,同时讨论波和水动力在不同流速下的非线性特性.
1 控制方程
定义坐标系oxy(图1),x轴和静水面重合,y轴垂直向上,在无波动时水深为h.Sf为瞬时自由表面,Sb为半圆柱表面(物面),其单位外方向矢量为N=(Nx,Ny).水底表面Sbot位置为y=-h,Sc为流体域∀的人工截断边界.假设流体为均匀、不可压缩和无粘性的理想流体,且流体的运动为无旋.半圆柱运动时流场速度势φ满足Laplace方程:
2φ=0 in ∀
(1)
若流场内存在大小为U0并沿x轴正方向的稳态流,则流场总的速度势为:
Φ=U0x+φ
(2)
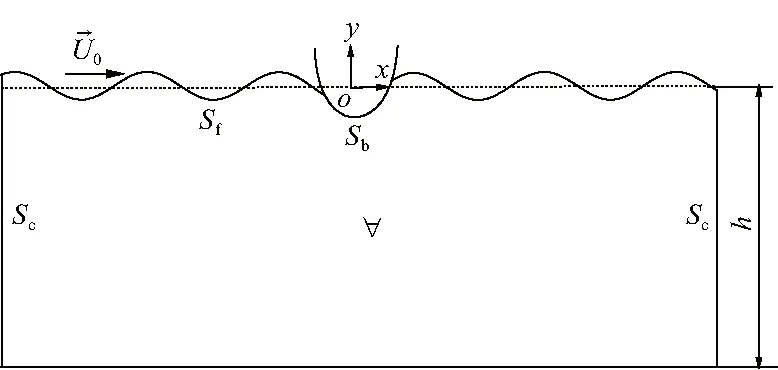
图1 坐标系Fig.1 Coordinate system
Φ在流场内也满足拉普拉斯方程以及边界条件:
ηt+Φxηx-Φy=0 onSf
(3)
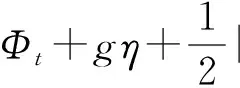
(4)
ΦN=φN+U0NxonSb
(5)
ΦN=0 ony=-h
(6)
以及在Sc上满足辐射条件.方程中t、g和η分别为时间、重力加速度和波高,下标表示对其的导数.将方程式(2)代入式(3)~(6)并将φ和η进行摄动,展开到二阶:
φ=φ(0)1+εφ(1)+ε2φ(2)+…
(7)
η=εη(1)+ε2η(2)+…
(8)
式中:ε为小量(一般可取为波陡);φ(0)为由水流作用引起的扰动势,而由其造成的波高忽略不计.φ(k)、η(k)(k=1,2)分别表示第k阶速度势和波高.同时,将水平位移X和角位移Θ也展开到二阶,在求解给定简谐运动的辐射问题时X和Θ只取到一阶,即X=εX(1),Θ=εΘ(1).将方程式(7~8)代入方程式(1~6)可得各阶(k=0, 1, 2)定解问题:
2φ(k)=0 in ∀(0)
(9)
(10)
(11)
(12)
(13)
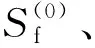
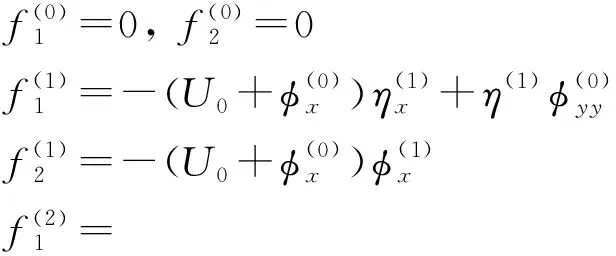
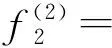
g(0)=-U0nx
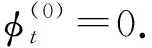
(14)
式中,p为压力,由Bernoulli方程有:
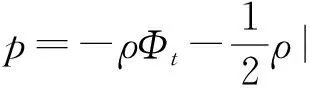
(15)
将式(2)代入式(15)再代入式(14)中并进行摄动,展开得:


2 数值方法与计算分析
混合边值问题式(9~13)通过有限元法求解:
Kφ(k)=F(k)(k=0,1,2)
(16)
式中:K为有限元系数矩阵;F(k)为右端向量,其元素表达式分别为:

式中,Ni为单元插值函数,文中采用12节点等参单元.由于该类单元形函数为三次插值,对其二次求导后仍保持连续,故可以方便而精确地计算出二阶导数,如方程式(10、11、12)中的φxx、φyy和φxy.
由于在时域内计算,每一时刻自由面上的波高和速度势必须知道,文中采用四阶Adams-Bashforth格式计算(t+Δt)时步自由表面波高和速度势.同时,采用人工阻尼区(图1)来吸收反射波[14],保证外传波条件.
对均匀流中半径为a的半圆柱绕射问题进行计算, 水深h=10a.半圆柱做水平或垂直运动:
Y=Asinωt
(17)
式中:A为运动幅值;ω为运动频率;t为时间.

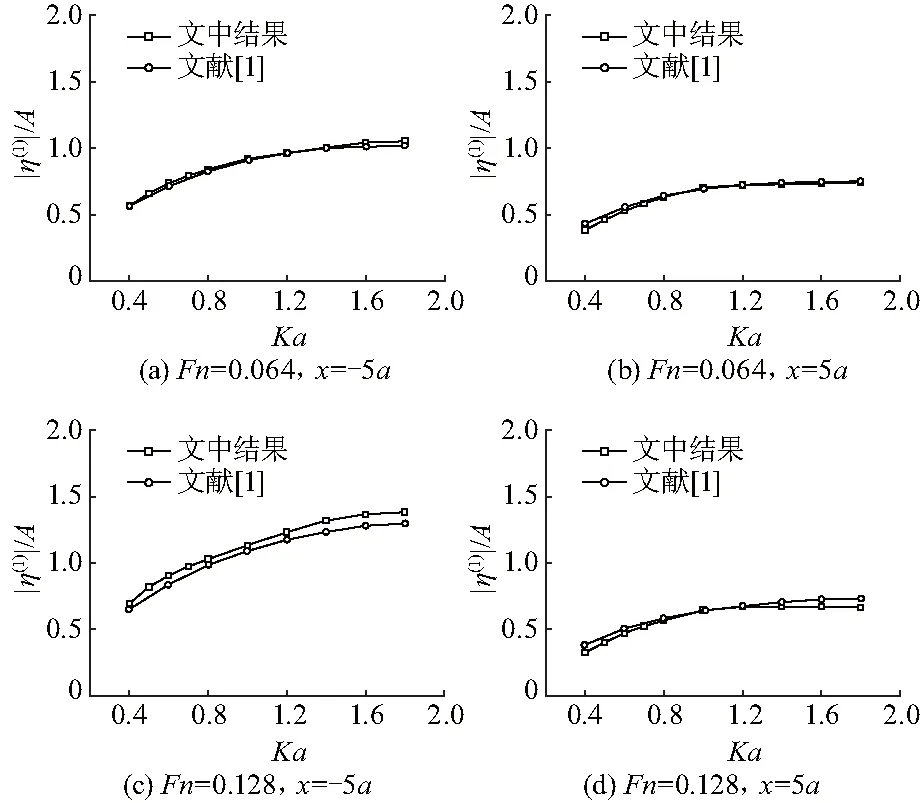
图2 一阶波幅值随Ka变化关系比较Fig.2 Comparisons of amplitudes of firstorder waves versus Ka
图3给出了Ka=1.0时半圆柱左右端(x=±a)线性(一阶)波和二阶波时间历程.3种不同付氏数Fn=0、0.064和0.128的计算结果在图中同时给出.从图中可以看出,半圆柱左端(x=-a处)线性波和二阶波均随付氏数增大而增大,而右端(x=a处)的情况正好相反.左端波变化更明显.这是因为半圆柱左端波向负x轴方向传播,而流的速度朝正x轴方向,两者相反;而在右端,波向正x轴方向传播,和流的方向相同,即多普勒效应.图4给出了Ka=1.0时两种付氏数Fn=0.064和0.128下线性与线性和二阶的合成波的对比.两者在波峰和波谷处均差异较大,这也表明在不同付氏数下波的非线性效应均较明显.
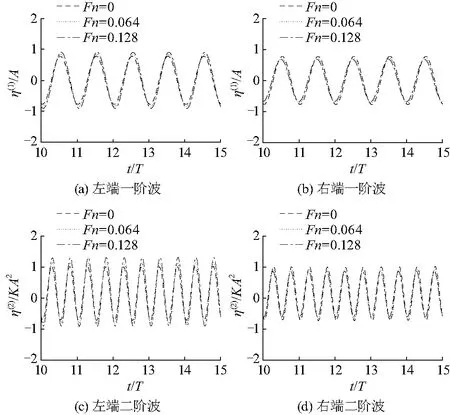
图3 Ka=1.0时一阶波和二阶波时间历程Fig.3 First-and second-order wave histories at Ka=1.0
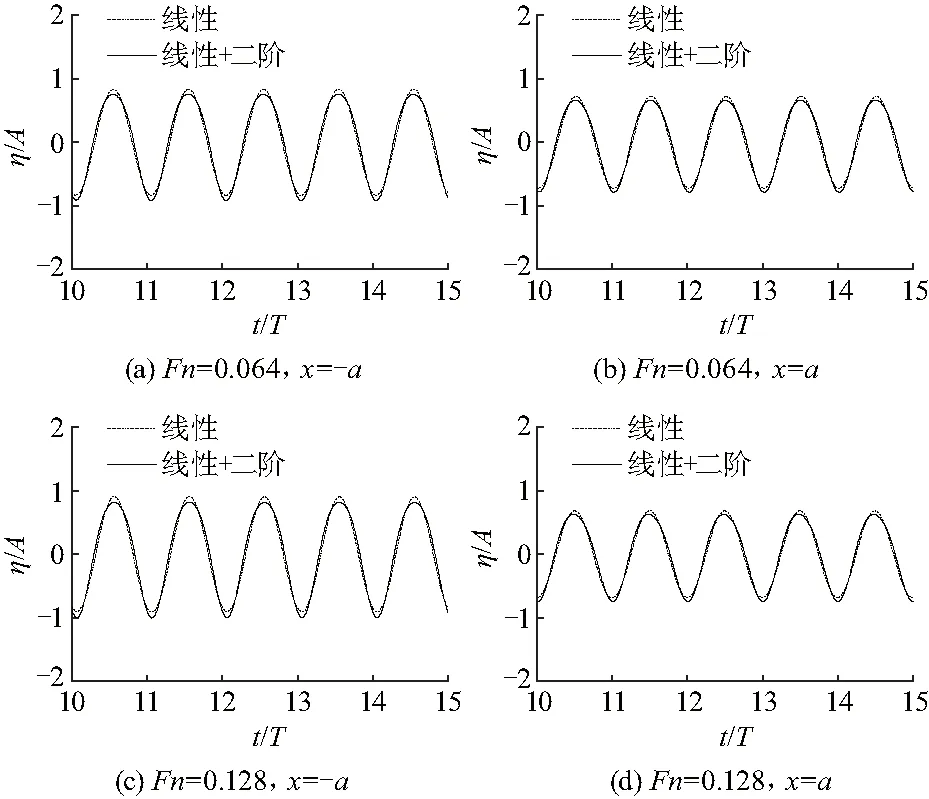
图4 波浪时间历程Fig.4 Histories of waves
图5、6给出半圆柱左右两端线性波和二阶波幅值随无因次波数Ka的变化关系.
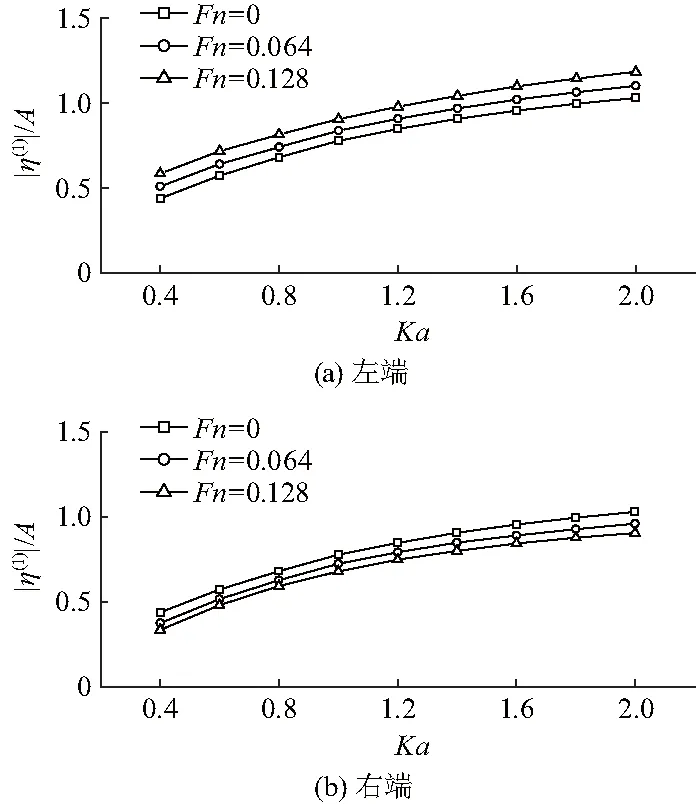
图5 一阶波幅值随Ka变化关系Fig.5 Amplitudes of first order waves versus Ka
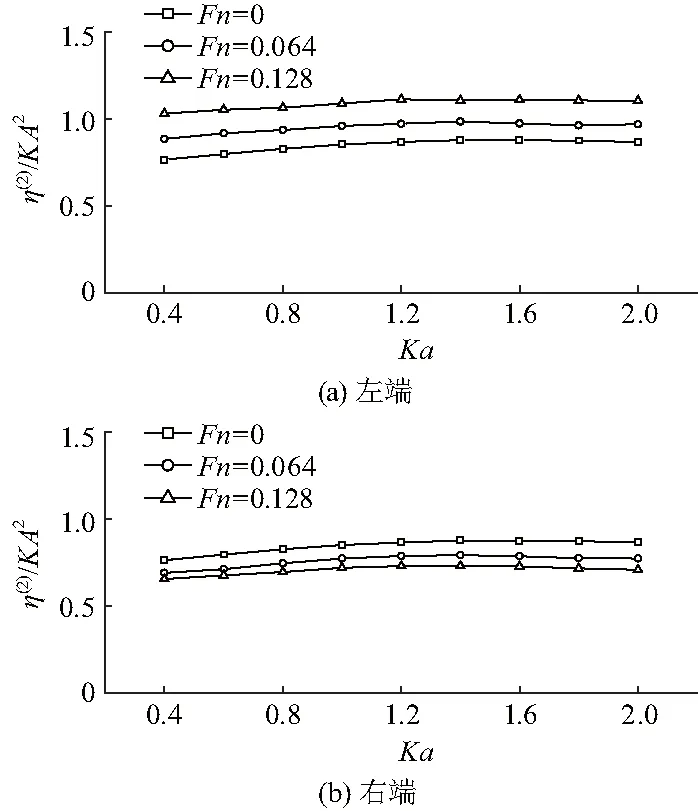
图6 二阶波幅值随Ka变化关系Fig.6 Amplitudes of second order waves versus Ka
从图5中可以看出,在同一付氏数下,左、右两端线性波幅值随Ka增大而稳定增大;而在同一无因次波数Ka下,左端线性波幅值随付氏数增大而增大,而右端情况相反.而二阶波(图6),其在同一Ka下随付氏数变化情况和一阶波类似,但在同一付氏数下随Ka增大而缓慢增加,随后近似趋于常数.
图7为时间t从4T到8T(T为线性波周期)时间内的线性波以及线性和二阶合成波的自由表面轮廓.从图中可以看出,半圆柱左端自由表面波的幅值较大而波长较短,而右端波幅值较小而波长较长,即多普勒效应.从图中可以看出,由于二阶波的影响,半圆柱左、右两端区域特别是半圆柱附近的波形存在一定的差异.

图7 A/a=0.1、Ka=2.0、Fn=0.128时从t=4T到8T时间内的波形轮廓Fig.7 Wave profiles at A=0.1a, Ka=2.0 and Fn=0.128for t=4T to 8T with time interval Δt=0.1T
图8给出了线性力(一阶力)和二阶力幅值在Fn=0、0.064和0.128时随Ka变化关系.
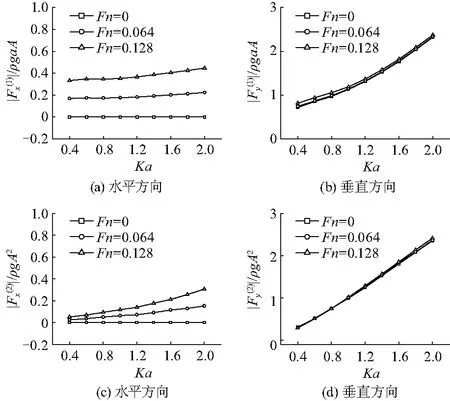
图8 线性和二阶力幅值随Ka变化关系Fig.8 Amplitudes of first and second orderforce components versus Ka
在Fn=0时,水平方向的线性力和二阶力因为对称性为零.在Fn=0.064和0.128时,水平方向的线性力和二阶力均随Ka增大而缓慢增大.这主要是因为水流的存在导致流场内的速度势不再关于y轴对称,进而在半圆柱表面上的速度分布也不再左右对称;而在垂直方向,在同一付氏数下线性力和二阶力随Ka增加较快.同时,3种不同付氏数下线性力和二阶力差别很小.图9为二阶平均力在3种不同付氏数下随Ka变化关系.在付氏数大于零时,在无因次频率0.4~2.0范围内,水平和垂直方向的平均力均为负值,且随着付氏数的增大而变小.
现在考虑半圆柱做水平运动时的情况.运动幅值仍取A/a=0.1.图10给出x=±5a处线性波幅值和文献[1]中的对比,在两种不同付氏数Fn=0.064和0.128下其对比结果均符合较好.图11给出了线性力以及线性和二阶的合成力的对比.在两种不同付氏数Fn=0.064和0.128下水平力几乎没有差别,而垂直力,在两种付氏数下其形态虽有所不同(图12(b,d)),但两者的非线性特性均非常明显.图13为一阶力和二阶力随Ka变化关系.3种不同付氏数下的水平一阶力差异较小并最终趋近于一常数.而垂直力有明显的差异.与一阶力相反,二阶力在水平方向差异明显,而在垂直方向则几乎没有区别.
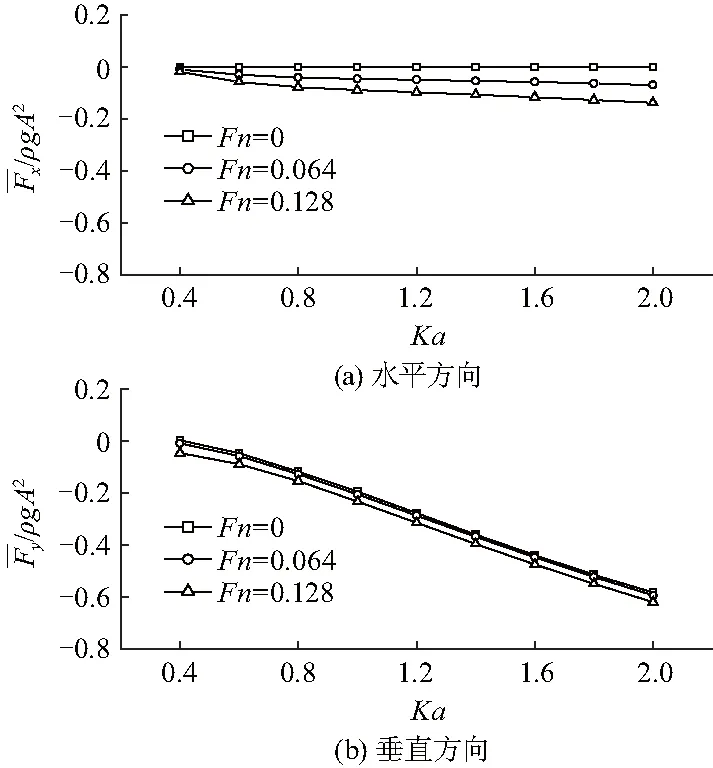
图9 二阶平均力随Ka变化关系Fig.9 Second order mean force components versus Ka

图10 比较一阶波随Ka变化关系Fig.10 Comparisons of amplitudes offirst order waves versus Ka

图11 Ka=1.0时水动力时间历程Fig.11 Histories of forces at Ka=1.0
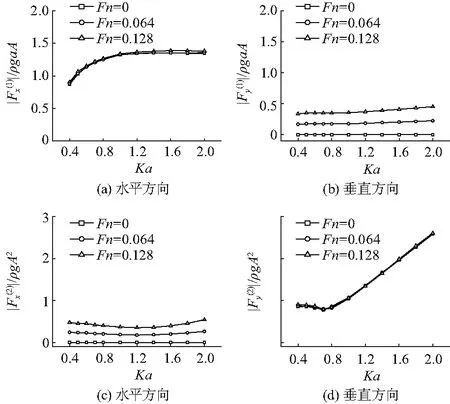
图12 一阶力和二阶力幅值随Ka变化关系Fig.12 Amplitudes of first-and second-orderforce components versus Ka
平均二阶力(图13)在水平方向变化较复杂.在Ka<1.3时小于零,其后随着Ka的增加其值增加为正值;而垂直方向的二阶平均力则均为负,而随着Fn的增大略微减小.

图13 二阶平均力幅值随Ka变化关系Fig.13 Second order mean force components versus Ka
3 结论
(1) 半圆柱上游区域(左端)和下游区域(右端)的一阶波和二阶波随付氏数的增大而增大,而下游波随付氏数变化情况则正好相反,而上游波在不同付氏数下非线性特性均较明显.
(2) 在做垂直运动时,水平力随付氏数不同而变化明显,而垂直力差异很小;在水平运动时,垂直线性力和水平二阶力随付氏数变化而明显不同,但水平线性力和垂直二阶力的差异很小.
