立足素养培育体验建构过程

2018-02-13王荣根于正华

物理教学探讨 2018年1期

关键词：建构主义规律概念

王荣根+于正华

摘要：本文以《圆周运动》相关概念及规律的教学设计为例，根据建构主义学习理论，说明学生的学习应该如何经历知识的发生、发现过程，以达到有效培育学生的物理核心素养。

关键词：建构主义；核心素养；概念；规律

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2018）1-0078-3

圆周运动是继平抛运动之后又一种比较特殊的曲线运动。对于平抛运动的研究，是根据运动的合成与分解“化曲为直”；而圆周运动是直接针对合运动的研究，故必须用特有的物理量来反映其特征，概括其规律。

从教学内容看，《圆周运动》一节的教学重点是对描述匀速圆周运动快慢的物理量的理解，难点是比较匀速圆周运动快慢的方法，是一节比较典型的物理概念教学课。

建构主义理论认为，人类的学习过程是一种主动建构的过程，是在已有知识的基础上不断地同化新的知识，或者是用已有的知识经验去顺应新知识的过程。圆周运动是典型的曲线运动，曲线运动是直线运动的延伸。研究曲线运动的方法与直线运动相比，有相似也有区别。基于建构主义的学习就是在相似和区别的分析和理解中进行的。

1 圆周运动的概念

圆周运动的定义内容很简单。从运动轨迹的角度看，我们把质点运动轨迹是直线的运动叫做直线运动；质点运动轨迹不是直线（曲线）的运动叫做曲线运动；质点运动轨迹是圆（或圆弧）的运动叫做圆周运动。但在实际教学中，有的老师是这样安排的，在一开始就展示电风扇的运动（图1）、钟表指针的运动（图2）、摩天轮的转动（图3）等，说它们的运动就是圆周运动。这种教学，学生不容易抓住圆周运动的本质。这实际上是混淆了圆周运动与转动的概念，一个看似简单的概念可能把学生搞得糊里糊涂。

物理学中的圆周运动指的是质点的运动；如果物体上的各点都在绕同一点（这一点可以在物体上，也可以不在物体上）做圆周运动，这样的运动叫转动。可见圆周运动与转动的最大区别在于对象是质点还是物体。

我们可以用一根细线，一端固定，另一端栓一个小球，让小球绕固定端做轨迹是圆的运动（如图4所示）；接着，说明地球（或其他行星）绕太阳的运动轨迹（如图5所示），可以近似看成是圆周运动；最后，说明转动的电风扇扇叶上任意一点的运动、表针转动时任意一点的运动……它们的共同特点是轨迹为圆，质点的这种运动就叫做圆周运动。转动的物体上各点都在做圆周运动。

2 线速度的概念

部分教材中，关于线速度概念的建立过程是：先说明最简单的圆周运动是匀速圆周运动，做匀速圆周运动的质点在任何相等的时间内通过的路程相等；接着，说明质点通过弧长与所用时间的比值可以描绘质点做圆周运动的快慢，这个比值就是线速度。这种设计容易让学生误认为线速度是一个全新的概念，没有考虑学生头脑中已有的关于速度的知识，纯粹是一种注入式教学。

直线运动，为了描述运动的快慢，建立了平均速度和瞬时速度的概念。这种描述运动快慢的方法完全适合曲线运动。这种观点在平抛运动中已渗透给学生，学生也比较容易接受。因此，对于用线速度描述质点做圆周运动的快慢，“另起炉灶”是不明智的，最合理的途径是“乘势而上”。

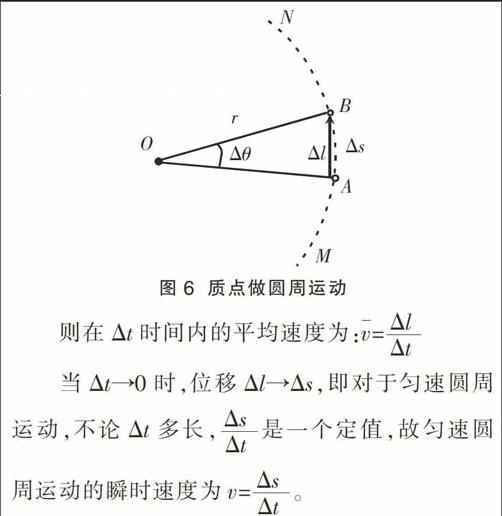
如图6所示，做圆周运动的质点在Δt时间内，从A点沿圆弧运动到B点，运动的位移是Δl，通过的弧长是Δs。

需要说明的是，跟直线运动一样，匀速圆周运动的平均速度跟哪段时间（或哪段位移）有关；匀速圆周运动的瞬时速度大小是不变的。为了跟后面学习的一种速度区别开来，我们把匀速圆周运动的瞬时速度称之为线速度。由此可见，线速度是瞬时速度概念在匀速圆周运动中的具体表现，而不是一种新的定义方法。

用同样的方法可说明匀速圆周运动线速度方向就是该点的切线方向，实验也能证明这个结论。

上述设计主要参考了赵凯华、张维善编撰的《新概念高中物理读本》。笔者认为，这是一种有利于学生顺利建构线速度概念的合理方案。

3 角速度的概念

3.1 角速度概念引入的必要性

学生在学习《圆周运动》这一节时，经常有这样的疑问：“描述圆周运动的快慢时，有了线速度，为什么还要再引入角速度呢？”

质点绕圆心做圆周运动时，总有一条有形或无形的“半径”在同时发生转动，运动的快慢与转动的快慢并不完全一致。例如，相同时间内，图7中质点A沿着大圆运动到A'，质点B沿着小圆运动一周，质点A的线速度大于B的线速度，但动画显示，这段时间内，连接质点B的半径转过了360°，而连接质点A的半径只转过了180°，明显看出质点B的半径转动得较快。由此可见质点运动（做圆周运动）的快慢与转动（质点与半径的连线）快慢具有不同的特征。物理学上为了描述转动的快慢，引入了角速度的概念（线速度描述了做圆周运动的物体通过弧长的快慢；角速度描述了物体与圆心连线扫过角度的快慢。）。

在图6中，做圆周运动的质点在Δt时间内，从A点沿圆弧运动到B点，半径OA在这段时间内转过的角为Δθ，它与所用时间Δt的比值，就描述了半径OA绕圆心转动的快慢，这个比值叫做角速度，用ω表示。

3.2 角速度与线速度的数量关系

还是在图6中，设质点做圆周运动的半径为r，当Δθ以弧度为单位时，即Δs=rΔθ，代入相应公式可得v=ωr。这表明在匀速圆周运动中，线速度的大小等于角速度大小与半径的乘积。

上述推导过程具有一般性。因此，这个结论不仅适用于匀速圆周运动，而且适用于一般圆周运动。

4 常见的两种传动模型

皮带傳动与同轴传动是两种常见的传动模型，关于这两种传动模型的特点，教师往往在教学中是直接告诉，学生也只能是死记硬背。

要研究传动模型的特点，必须建立在线速度和角速度概念的基础上，分析在传动的过程中，相同时间内通过的弧长或圆心角的大小关系。

如图8所示，皮带传动是通过摩擦进行的传动。设在时间Δt内，主动轮边缘上的某一点A转到A'，转过的弧长为Δs，在不打滑的情况下，从动轮边缘上的任一点（如B点）所转过的弧长一定也是Δs。由此可见，跟皮带接触的轮缘上各点，线速度大小相等。同理可证，齿轮传动具有同样的特点（如图9所示）。

对于同轴传动装置（如图10、11所示），装置上面的各点，在相同的时间内转过相等的角度，故这些点的角速度是相等的。

教学中可以借助模拟动画，让学生直观感受到这些特点，经历模型建构过程，从而加深理解。

对于《圆周运动》的教学，就知识而言结论比较简单，但是结论的建构过程蕴涵丰富的教育原理，而且只有通过学生主动建构的知识才是最牢靠的。从核心素养的培育角度出发，着眼学生的可持续发展，让学生经历知识的发现过程跟知识本身相比是同等重要的。

参考文献：