一种基于对角加载的特征子空间抗干扰算法

2018-02-13徐少波

无线电工程 2018年11期

夏辉，徐少波，徐如

(1.中国人民解放军92728部队，上海 200436； 2.中国电子科技集团公司第五十四研究所，河北石家庄 050081)

0 引言

北斗卫星导航系统[1]是我国自主研制的卫星导航系统，能够提供全天候、全方位的导航、定位、授时[2]和短报文服务，在国防和经济建设中发挥了重要作用。近年来，全球卫星导航系统更是在世界各个国家得到迅速的普及和应用。但是由于卫星信号功率很低，军事上经常存在敌方的有意电磁波干扰以及卫星导航应用电磁波环境的日益复杂[3]，导航终端很容易受到干扰信号的影响而无法正常工作。因此，目前各国都很重视卫星导航系统抗干扰技术[4]的研究。在此背景下，研究导航接收机抗干扰技术具有非常重要的意义。

在卫星导航自适应调零天线[5]抗干扰领域中，功率倒置(PI)[6]算法应用最为广泛，该算法的本质是一种空域滤波抗干扰技术。PI算法不需要预先知道有用信号的特性和干扰入射方向等先验信息，对强干扰环境中微弱信号的接收非常有效[7]，能使卫星导航接收机的抗干扰能力提高50 dB以上，具有很高的工程应用价值。然而在实际环境下，会存在各种非理想因素，如各通道之间幅相不一致[8]、过强期望信号[9]、干扰扰动和导向矢量失配[10]都会带来PI算法性能的严重下降[11]。针对上述问题，本文提出一种基于对角加载[12]的特征子空间[13]抗干扰算法，以改善PI算法的稳健性。

首先给出了PI算法的自适应调零抗干扰技术数学模型，并对基于对角加载的特征子空间抗干扰算法进行了详细分析，通过仿真试验，对比分析了传统PI算法与DL-ESB-PI算法，相对于传统PI算法，DL-ESB-PI算法在小快拍[14]、强期望信号等非理想环境下依然保持了优异的性能，为自适应调零抗干扰天线的算法研究及工程实现提供了理论支撑。

1 功率倒置抗干扰算法模型

考虑M元等距线阵，阵元间距为d，并且假设阵元均为各向同性阵元。远场处一个期望信号和P个互不相关的远场窄带干扰信号[15]入射到阵列上，设到达角分别为θ0和θk(k=1，2，…P)，阵列接收的快拍数据表示为：

X(t)=AS(t)+N(t)，

(1)

阵列的协方差定义为：

(2)

然而，实际处理中，阵列协方差矩阵无法得到，通常用有限次快拍计算得到其最最大似然估计[16]为：

(3)

式中，

X=[Xi+n(nK+1),Xi+n(nK+2),...,Xi+n(nK+K)]为第n个快拍数据块，每个块含K个快拍。

功率倒置抗干扰算法是在特定阵列通道的增益为常数的条件下，最小化阵列输出功率。可以描述为：

(4)

式中，a0是只有一个元素为1、其余元素全为0的列向量，若a0=[1,0,0,...,0]T，表示约束天线阵列的第一通道加权值始终为1；Rxx为输入数据的协方差矩阵；W为待求解的权向量。通过拉格朗日乘子法可以得到功率倒置权向量[17]为：

(5)

进一步化简，省去常数因子α，得

(6)

功率倒置抗干扰算法模型如图1所示。

图1 卫星与观测点的关系

2 基于对角加载的特征子空间抗干扰算法

2.1 对角加载

在复杂的电磁环境中，由于通道误差、阵列位置误差及互耦[18]等因素的存在，使得功率倒置抗干扰(PI)算法的性能大幅下降。为了提高波束形成算法的稳健性，对协方差矩阵做对角加载处理，

RDL-PI=Rxx+εI，

(7)

式中，Rxx为上节计算得到的协方差矩阵；I为M×M维的单位阵；ε为对角加载量；RDL-PI为经过对角加载的新协方差矩阵。对角加载ε通常很难确定[19]。当加载量过大时，会影响干扰抑制效果；而当加载量过小时，对于传统PI算法稳健性改善不明显。针对这种情况，采用一种动态地确定加载量ε的方法。理想情况下，真实协方差矩阵中的对角元素相同，但是估计的协方差矩阵中每个元素都存在一定的误差。因此可通过利用采样协方差矩阵Res的对角元素求平均得到真实的协方差矩阵Rxx的对角元素；估计误差可通过利用Res的对角元素的标准偏差求得[20]。则对角加载因子ε满足

std(diag(Res))≤ε≤trace(Res)/M，

(8)

式中，std表示标准偏差；trace表示矩阵的迹；diag表示取矩阵的对角元素。

2.2 特征子空间抗干扰算法

在实际应用环境中，某些情况下会存在期望信号功率较强的场景，此时，传统PI算法会将期望信号也当成干扰信号抑制掉，导致输出信干噪比降低，接收机无法定位。针对这种情况，本文采用特征子空间抗干扰(ESB)方法来提高算法稳健性。

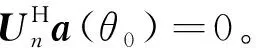
设阵列协方差矩阵Rxx的特征分解[22]为：

式中，Us表示信号特征向量，包含P个干扰及1个期望信号；Λs为对应的大特征值组成的对角阵；Un表示噪声特征向量，代表噪声信号，其维数为M-P-1；Λn为小特征值组成的对角阵。ESB算法在传统PI算法的基础上，舍弃噪声子空间对抗干扰权值的贡献，即

(9)

2.3 基于对角加载的特征子空间抗干扰算法

本文将对角加载与特征子空间算法结合，进一步提高PI算法的稳健性，并且适用于强期望信号的场景。基于对角加载的特征子空间抗干扰算法即使在小快拍数据、存在阵列误差等非理想环境下，依然可以保持优异的性能。

下面给出基于基于对角加载的特征子空间抗干扰算法的计算公式：

(10)

式中，UDL-S为经过对角加载处理后的信号特征向量。

基于对角加载的特征子空间抗干扰算法模型如图2所示。

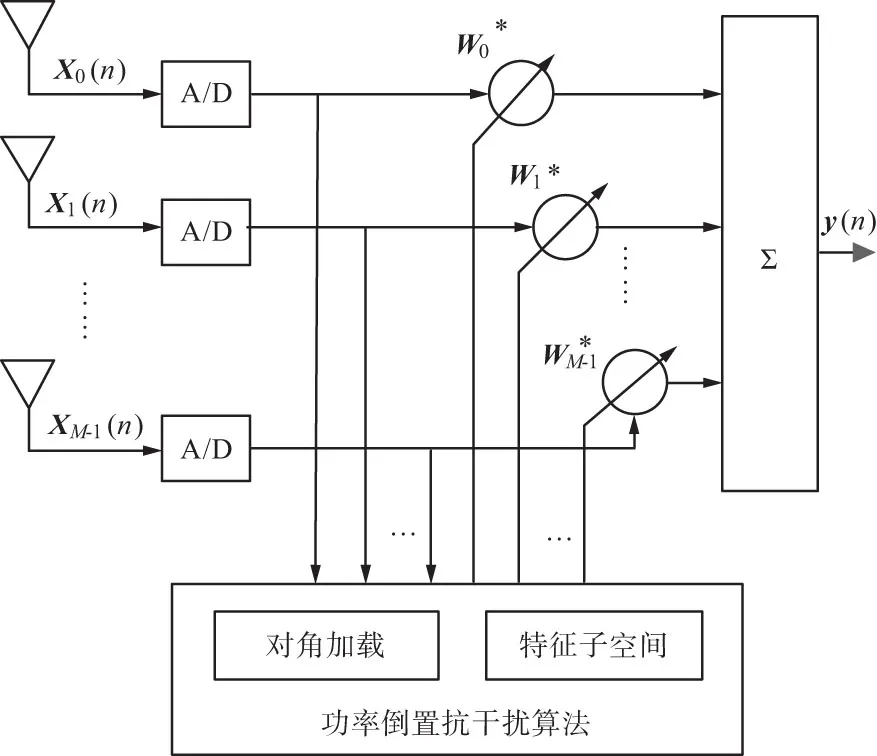
图2 基于对角加载的特征子空间抗干扰算法

3 仿真分析

仿真实验1：采用20阵元线阵，阵元间距为0.5λ，载波频率为f1=1 268.52 MHz，接收机接收到的北斗信号经过下变频处理以后中频信号频率fc=46.52 MHz，信号带宽为20.46 MHz，采样频率fs=62 MHz。噪声功率为-101 dBm。期望信号入射角度为0°，信噪比(SNR)为-30 dB，干扰信号入射角度为30°，干噪比(INR)为80 dB。协方差计算快拍数为40时，传统PI算法与本文给出的DL-ESB-PI算法的方向图对比如图3所示。随快拍数变化，2种算法的输出信干噪比变化曲线如图4所示。

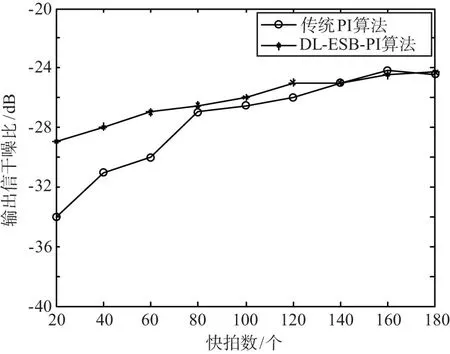
图3 快拍数为40的PI与DL-ESB-PI算法对比

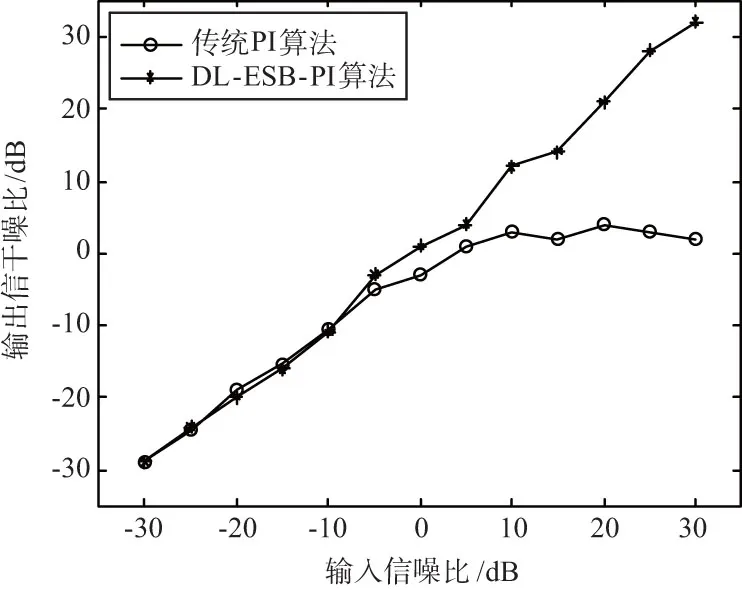
图4 随快拍数变化2种算法输出信干噪比对比

由图3可以看出，当计算协方差快拍数为40时，PI算法与DL-ESB-PI算法均能够在干扰位置形成零陷，而PI算法在除干扰位置外，多个角度形成了深浅不一的零陷，DL-ESB-PI算法的副瓣则更加平滑，对期望信号的损失更小，稳健性更高。

由图4可以看出，当快拍数较少时，DL-ESB-PI算法的输出信干噪比明显高于PI算法，直到快拍数达到140左右，2种算法的输出信干噪比才基本一致，进一步体现了DL-ESB-PI算法在小快拍数下的稳健性。

仿真实验2：采用20阵元线阵，阵元间距为0.5λ，载波频率f1=1 268.52 MHz，接收机接收到的北斗信号经过下变频处理以后中频信号频率fc=46.52 MHz，信号带宽为20.46 MHz，采样频率fs=62 MHz。噪声功率为-101 dBm。期望信号入射角度为0°，信噪比(SNR)为10 dB，干扰信号入射角度为30°，干噪比(INR)为80 dB。当输入信噪比为10 dB时传统PI算法与本文给出的DL-ESB-PI算法的方向图对比如图5所示。随输入信噪比变化，2种算法的输出信干噪比变化曲线如图6所示。

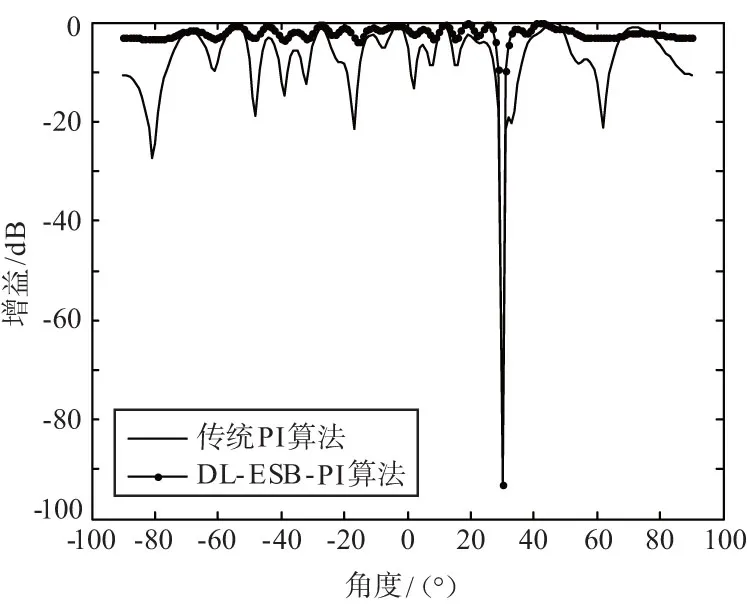
图5 PI算法与DL-ESB-PI算法方向图对比

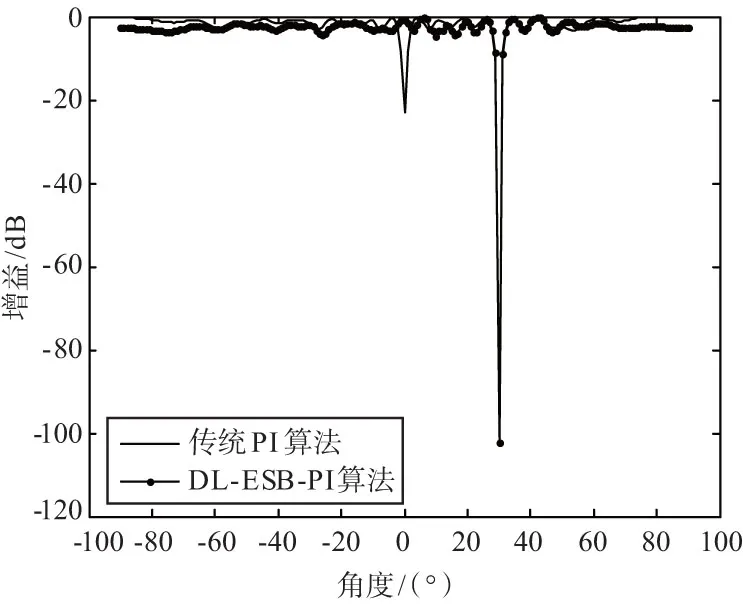
图6 输入信噪比变化时2种算法的输出信干噪比对比

由图5可以看出，当期望信号较强，即输入信噪比较强时，PI算法不能分辨强信号为期望信号还是干扰信号，因此在期望信号位置与干扰位置均形成了零陷，区别仅是零陷的深浅有所差异；而DL-ESB-PI算法的信号子空间包含期望信号特征矢量，因此生成的权值不会对期望信号进行抑制，不会在期望信号位置形成零陷，仅抑制干扰，稳健性更高。

由图6可以看出，当输入信噪比较低时，2种算法的输出信干噪比非常接近，随着输入信噪比加强，当输入信噪比达到0 dB或更强时，DL-ESB-PI算法的输出信干噪比明显高于PI算法，这就是因为PI算法对期望信号也进行了抑制，而DL-ESB-PI算法则对期望信号无损失。

通过上述2个仿真实验可以看出，DL-ESB-PI算法相比传统PI算法在小快拍及强期望信号场景下具有更加优秀的性能，稳健性更高。

值得一提的是，本文提出的DL-ESB-PI算法在期望信号较强且存在强干扰环境下保持了优异的性能，但当仅存在强期望信号或强干扰时，需要对特征空间做进一步处理，以避免期望信号被抑制。