基于量子衍生的遥感图像边缘检测方法

柯余仙，毕思文

(中国科学院遥感与数字地球研究所，北京 100101)

0 引言

一副图像的边缘包含了图像的大部分信息，在实际应用中尤其是遥感图像，其边缘的提取，对后续的图像分割、特征提取和目标地物识别等起到了至关重要的作用。经典的边缘提取算法有Prewitt算子、Sobel算子和Canny算子等，Prewitt算子和Sobel算子是基于领域间隔为2的差分运算[1]，忽略了中心像素自身的灰度值，边缘检测效果不太理想。Canny算子[2]仍然是现在应用最广泛的边缘检测算子，虽然其检测精度和抗噪性能要远远优于Prewitt算子和Sobel算子，但需要人工干预，选取最佳阈值，实时性较差。近些年来，基于这些经典的边缘检测方法，也有许多学者提出了新的算法，如数学形态学边缘检测算法[3]、人工神经网络边缘检测算法[4]、人工鱼群算法[5]和遗传算法[6]等。

量子衍生思想是受人工神经网络、遗传算法等自然规律衍生出来的算法的启发，然后利用量子力学的概念、原理以及公理化数学体系改进已有的算法或者开发新算法，应用在经典计算机上[7]。2007年，谢可夫等人[8]基于量子力学、量子信息等理论与概念，提出了量子衍生形态学边缘检测，该方法具有检测噪声污染图像的优点，但不如普通图像边缘检测优越。2016年，S.Abdel-Khalek[9]等人提出基于量子熵的图像边缘检测算法，通过计算图像的量子熵，来确定图像分割阈值，提取图像边缘。

2001年初，遥感地球所毕思文院士首次提出了量子遥感[10]的概念，经过17年多的研究，创建了量子遥感理论与技术体系框架[11]。在此基础上，毕思文院士带领其团队在2014年提出了量子遥感图像处理的概念，实现了量子遥感图像去噪、量子遥感图像增强和量子遥感图像分割等量子遥感图像处理技术[12]。本文借鉴量子叠加态的三量子位态矢正反跳变特性，并结合边缘的多方向性，构造出3×3的12方向模板边缘检测算子对遥感图像进行边缘提取，进一步完善了量子遥感图像处理体系。

1 量子理论

1.1 量子比特

比特是经典计算机的基本储存单位，其状态处于0或1。经典计算机的一比特等价于量子物体的2种不同的组态或状态，称为量子比特[13]。与经典比特不同的是，由于量子叠加态的原理，一个量子系统可以同时处于|0>和|1>之间，即

|φ>=a|0>+b|1>，

(1)

式中，a和b是复系数，分别表示出现0态矢和1态矢的概率，若|0>和|1>是相互正交的，则a和b满足归一化条件，即

a2+b2=1。

(2)

一个系统|φ>由n个子系统构成，子系统的状态为{φ1，φ2，φ3，......，φn}，根据量子力学的第四假设[14]，该复合系统的状态为：

|φ>= |φ1>⊗|φ2>⊗|φ3>⊗......⊗|φn>=

(3)

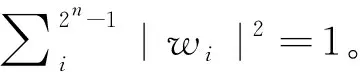
1.2 量子Hadamard变换

根据量子力学的第三和第四假设[14]，利用单比特量子门Hadamard(简记为H)作用于式(1)，得

H|φ>=H(a|0>+b|1>)=

(4)

式中，

(5)

2 灰度图像的量子比特表示与像素的叠加态关联

2.1 经典图像的量子比特表示

设f(m，n)为一副数字图像，(m，n)∈z2。f(m，n)是归一化处理后的图像，其像素值大小范围为[0，1]，f(m，n)表示图像在(m，n)处的灰度值。根据式(1)以及文献[15-16]，可以将灰度图像表示为量子比特的形式：

(6)

这里，|0>和|1>分别对应着经典图像的黑点与白点，即二值化图像的像素值取“0”或“1”。1-f(m，n)表示在位置(m，n)处图像的像素值取0的概率，f(m，n)表示在位置(m，n)处图像的像素值取1的概率，显然它们满足归一化条件。

2.2 图像像素的叠加态关联分解

在3×3窗口中，设中间像素(m，n)的值为fm，n，邻近像素值为fi，j，m-1≤i≤m+1，n-1≤j≤n+1，如图1所示。

fm-1,n-1fm-1,nfm-1,n+1fm,n-1fm,nfm,n+1fm+1,n-1fm+1,n-1fm+1,n+1

图13×3像素关联

以水平方向为例，按照式(3)，可得如下三量子位的复合系统：

|fm，n-1fm，nfm，n+1>= |fm，n-1>⊗|fm，n>⊗|fm，n+1>=

(7)

图2 lena分解子图

3 量子衍生边缘检测算法

常见的经典边缘检测算子有一阶微分算子Prewitt，Sobel，Robert；二阶微分算子LOG，Canny。Canny算子的构成基本分为4步[17]：先用高斯滤波器平滑图像；再用一阶偏导的有限差分来计算梯度的幅值和方向；接着用非极大值抑制的方法增强梯度图像；最后设置高低阈值来检测和连接边缘。在量子理论的基础上，受Canny算子的启发，本文研究了基于量子衍生的边缘检测算子，具体步骤如图3所示。

图3 量子衍生边缘检测流程

3.1 量子衍生中值滤波

利用式(4)和式(5)对式(6)进行量子Hadamard门操作，得

(8)

根据量子系统的测量和坍缩原理[18]，若对图像中某点经过Hadamard变换后的新态矢H|fm，n>进行测量，则得到|0>的概率为：

(9)

由式(9)可以看出，当图像中该点为黑点或者白点(即“0”或“1”)时，此式的等号才能成立。在0和1之间的任何一个数值都会使此式的值大于0.5。而噪声中典型的椒盐噪声正好符合这一特性，可以利用此式并结合条件中值滤波[19]去除遥感图像中的椒盐噪声。

3.2 量子衍生边缘检测算子的构成

分析图2中的各个子图可以看出，态矢|110>，|011>，|100>和|001>对应的4幅子图图2(d)、图2(h)、图2(g)和图2(e)存在着灰度边缘的变化，并且在态矢|110>和|100>中，对于中间的量子位来说发生了跳变情况，由图像的量子比特定义可知，此现象正好对应灰度图像3个相邻像素中，中间像素值发生了跳变。由此，是定义|110>和|100>两个态矢表示图像灰度值的反跳变，|011>和|001>两个态矢表示图像灰度值的正跳变。在此，将构成提跳变的2个量子位进行取反操作，则得到对应态矢的反态矢，如态矢|110>的反态矢是|101>，它们的概率差正好反映了该处发生灰度跳变的可能性大小，即是图像边缘的可能性大小。水平方向的4个态矢正反跳变的概率分别为：

正跳变：

|w011|2-|w101|2=(fm，n-fm，n-1)*fm，n+1，

|w001|2-|w010|2=(fm，n+1-fm，n)*(1-fm，n-1)。

(10)

负跳变：

|w110|2-|w101|2=(fm，n-fm，n+1)*fm，n-1，

|w100|2-|w010|2=(fm，n-1-fm，n)*(1-fm，n+1)。

(11)

为了得到更加精确的边缘检测模型，本文提出用2个正态矢或者2个反态矢的算术平均值作为灰度的跳变概率，即

(12)

(13)

(14)

(15)

其他方向上的算子由此类推。6个方向，一共12组算子，其中6个水平模板构成了水平方向上的边缘检测算子，6个垂直模板构成了垂直方向上的边缘检测算子。本文提出，在水平方向上分别取正负2个方向算子的平均值的最大值作为水平检测分量Gx，在垂直方向上分别取正负2个方向算子的平均值的最大值作为垂直检测分量Gy，即

(16)

(17)

最后，取水平检测分量与垂直检测分量的梯度绝对值之和作为最终的边缘检测结果，即

G(m，n)=|GX|+|Gy|。

(18)

3.3 边缘二值化提取

本文采用单一阈值，并根据Canny算法的非极大值抑制思想对3.2节得到的灰度边缘图G进行二值化提取，得到二值化边缘图E，具体算法步骤如下：

① 单一阈值为边缘梯度图像的均值，即t=mean(G(：))；

② 对边缘梯度图G进行非极大值抑制二值化，若

(G(m，n)>t)&&{[(Gx(m，n)>Gy(m，n))&&(G(m，n)>

G(m，n-1)&&(G(m，n)>G(m，n+1)]

||[(Gy(m，n)>Gx(m，n))&&(G(m，n)>

G(m-1，n)&&(G(m，n)>G(m+1，n)]}，

则E(m，n)=1，否则E(m，n)=0；

③ 输出边缘二值化图E。

3.4 量子衍生边缘检测函数

本文将量子衍生中值滤波，量子衍生边缘检测算子封装在一个量子衍生边缘检测函数中，即

functionE=Qedge(f)，

式中，f为对原灰度图I进行归一化之后的灰度图，将像素值归一化到[0，1]之间；E为最终的二值化边缘检测图像。

4 实验结果分析

利用3.4节提出的量子衍生边缘检测函数Qedge()，可以有效地检测出结构复杂并含有椒盐噪声的遥感图像边缘图。在Matlab2016的环境下分别对复杂的街景图和航拍遥感图进行了仿真实验，在此基础上对加噪的航拍遥感图片(加上噪声强度为0.03的椒盐噪声)也进行了仿真实验，并将这些结果与经典的Sobel算法和目前较优的Canny算法进行的比较，效果如图4、图5和图6所示。

图4 街景图

图5 遥感航拍图

图6 加噪遥感航拍图

4.1 主观评价

根据3组实验，对比各种算法的仿真实验结果，可以看出本文提出的量子衍生边缘检测算法对于复杂的图像边缘定位更加准确，优于Sobel算法与Canny算法。如图4的4幅图右上角的屋檐瓦片和右下角的树木，Sobel算法和Canny算法都没有检测出来，而本文提出的算法，对于这些微小的精细结构的边缘检测定位精确，检测效果更优。在图6中，可以看出，对于含有椒盐噪声的复杂遥感图像，Sobel算法基本丧失了能力，Canny算法产生了轻微的通心粉效应，去噪不彻底，而本文提出的边缘检测算法几乎不受噪声的影响，边缘检测定位精确，去噪能力彻底。

4.2 客观评价

为了更直观地反映出各个算法的性能，采用一种基于连通域的边缘评价方法[20]来客观地评价图像边缘检测效果。即统计一幅图像的边缘点个数E，4-连通域个数(C4)与8-连通域个数(C8)以及它们之间的比值(C8/C4)，比值越小，则说明边缘的线性连接度越好，漏检、错检的概率就越小。街景边缘图统计结果如表1和表2所示。

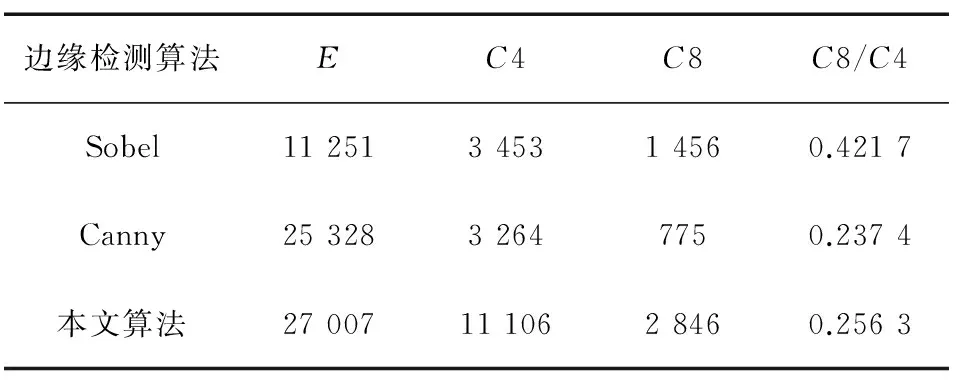
表1 第1组街景边缘图统计结果

表2 第2组遥感航拍边缘图统计结果

分析表1和表2可知，Sobel算子检测到的边缘数最少，Canny算子其次，而本文检测到的边缘数最多，这说明了本文边缘检测算法精度较高，能检测到精细结构的边缘，这与主观评价结果一致。不足的是，本文算法的C8/C4较小于Canny算法，说明本文算法在边缘连接性上没有Canny算法优越，但大大优于Sobel算法，这一结论与图片视觉效果相吻合。

5 结束语

基于量子比特与量子叠加态的理论，构造了基于量子衍生的边缘检测算法，并将其应用于复杂的遥感图像。仿真实验结果表明，提出的边缘检测函数不仅能检测出结构精细复杂的遥感图像边缘，而且还能从受椒盐噪声污染的遥感图像中有效地检测出其边缘信息。在后续工作中，可以将本文量子衍生边缘检测思想与频域相结合，利用频域的优势进一步加强提高遥感图像边缘检测的精确度与信噪比，以及边缘的连接性。