OQAM/OFDM系统中快速时变信道和CFO联合估计

刘晓鹏，陈西宏，肖 军

(1.中国人民解放军93636部队，天津 301611； 2.空军工程大学 防空反导学院，陕西 西安 710051)

0 引言

偏移正交幅度调制的正交频分复用(Offset Quadrature Amplitude Modulation/Orthogonal Frequency Division Multiplexing，OQAM/OFDM)[1-2]利用正交多载波技术和原型滤波器良好的时频聚焦特性，能够提升系统传输容量和抗符号间和载波间干扰的性能。OQAM/OFDM相比于单载波系统更容易受到载波频率偏移的影响[3-4]。载波频率偏移(Carrier Frequency Offset，CFO)往往还会和非理想的弥散信道相互影响[5-6]，一起对系统的解调信号产生影响，难以将二者分开进行估计。同时将二者进行联合估计能够获得更优的估计性能[7-8]。目前现有文献提出的联合估计方法都是在信道为慢衰落呈现慢时变特性时的基础上实现的[9-10]，没有考虑信道呈现快速时变特性时的估计。当信道快衰落速率增大时，快时变特性使得估计信道频率响应不能满足实时估计的需求。目前还没有相关文献针对快速时变信道和频偏的联合估计提出相应方法。

因此本文主要研究OQAM/OFDM系统在快速时变条件下的信道和CFO联合估计方法。在无线传输系统中，虽然信道的多径的复增益是不断变化的，但是信道的各径时延在几个数据块内可以看作是准时不变的，可以利用这种特性，采用基扩展(Basis Expansion Model，BEM)模型可以将时变信道拟合为几个固定基函数表示时不变信道，使得待估计的信道参数数量减少，可以很方便地对信道进行分析[11-12]。针对双选信道下OQAM/OFDM系统的CFO和信道进行联合估计，为了减少信道的估计复杂度采用了BEM信道模型，进而利用期望最大化(Expectation Maximum，EM)算法实现CFO和信道的联合估计。在EM算法中，将CFO作为待估计的参数，信道BEM参数作为隐藏变量，通过EM算法的迭代过程提升估计精度。

1 OQAM/OFDM系统及其信道估计

OQAM/OFDM系统发送端发送的信号[13-14]可以表示为：

(1)

式中，am，n表示n时刻、m子载波上的OQAM实值符号，是由复数符号的实部符号与虚部符号分离后引入一个时间偏移的得到的；M为子载波个数；gm，n(t)为原型滤波器的时频变换形式，可以表示为：

gm，n(t)=g(t-nτ0)ej2πmv0tejφm，n，

(2)

式中，g(t)表示原型滤波器；τ0为符号间的时间间隔，即实部和虚部符号之间的时间偏移；v0为子载波间隔，满足v0τ0=1/2。φm，n=(π/2)(m+n)+φ0是由于OQAM符号正交偏移特性产生的相位，φ0可以任意选择，本文中采用φ0=-mnπ。

调制符号经过脉冲响应为h(t，τ)无线多径信道，引入频偏Δf=θv0后，接收端接收到的信号可以表示为：

(3)

式中，θ为相比于系统子载波间隔的归一化频偏；Δ为多径信道的最大传播时延；n(t)为零均值、方差为σ2的加性高斯白噪声。

若τ∈(0，Δ)，由于原型滤波器的聚焦特性可以做如下假设[15]：

g(t-τ-nτ0)≈g(t-nτ0)。

(4)

在接收端对接收信号进行解调，时频格点(m0，n0)处的解调符号可以表示为：

(5)

当信道为快速时变时，若每一个采样信号的信道参数都是不一样的，并且存在归一化频偏，则第q时刻的OQAM/OFDM解调符号向量可以表示为：

yq=HqXq+ηq，

(6)

式中，

yq=[y0，q，y1，q，…，yM-1，q]T；

ηq=[η0，q，η1，q，…，ηM-1，q]T；

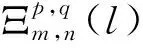
(7)

或者还可以采用物理信道参数(包括各径的时延τl和信道复增益αl，q(kTs))表示：

(8)

式中，L′为信道抽头个数；L为信道多径数目；τl为采用周期Ts归一化时延。信道的复增益中的L个元素是互不相关的，而hl，q(kTs)中的L′个元素是互相关的，并且信道抽头和信道复增益都是广义平稳的。在下述分析中，采用物理信道参数对信道进行建模。

2 BEM信道模型

在快速时变信道中，每一个OQAM/OFDM符号需要对信道每条径的复增益估计M个样本。若信道的径数有L个，则在每一个数据块内总共需要估计LM个参数。为了降低估计复杂度，考虑使用BEM信道模型，利用BEM模型对时变的信道复增益αl，q(kTs)进行建模。采用BEM模型的目的是将αl，q(kTs)构建成一组基函数的权值和：

αl，q=αBEMl，q+ξl，q=B×cl，q+ξl，q，

(9)

式中，αl，q表示信道第l径在第q个OQAM/OFDM符号时间内的复增益向量；B=[b0，b1，…，bNc]表示包含Nc个基函数bd的矩阵，其维度为M×Nc；cl，q=[cl，q[0]，cl，q[1]，…，cl，q[Nc-1]]T表示第q个信道第l径复增益的BEM参数向量；ξl，q表示相应的模型误差，一般假设为MSE最小化的误差。此时，最优BEM参数以及相应的模型误差为：

(10)

式中，S=B(BHB)-1BH为M×M矩阵。

现有的BEM模型包括Karhuen-Loeve BEM模型(KL-BEM)[16]、多项式BEM模型(Polynomial-BEM，P-BEM)[17]以及复指数BEM模型(Complex Exponential BEM，CE-BEM)[18]。

3 基于EM方法的CFO和BEM信道联合估计

期望最大化(Expectation Maximum，EM)算法[19-20]是一种用于解决不完备数据估计的最大似然估计算法，具有实现简单、迭代过程收敛性好的特点，长期以来在信道估计等多个研究领域都得到了广泛的应用。

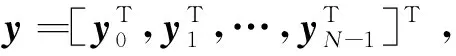
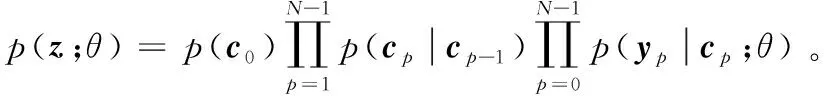
(11)

完备数据的对数似然函数可以表示为：

(12)

式中，C为常数。

下面采用EM算法对CFO和信道参数进行联合估计。首先构建期望函数，对于接收符号和上一次迭代的结果可得：

(13)

代入式(11)，并移除与θ无关的项后可以得到：

(yp-Ωq(θ)cq)H]}。

(14)

从式(14)中可以得到：

(15)

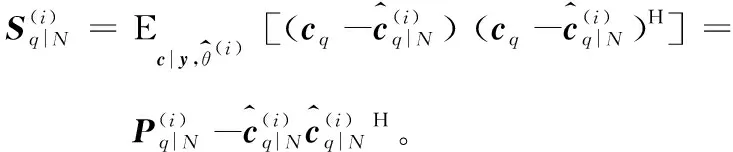
(16)

M步中对期望函数求最大，得到第i+1次迭代的频偏估计：

(17)

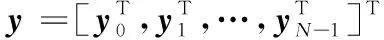
(18)

混合待估计参数向量为κ=[αT，θ]T中包含确定性的参数CFO以及随机参数，因此可以采用混合CRB(hybrid CRB，HCRB)来衡量本节所提方法的性能，HCRB矩阵可以表示为：

(19)

并且可以分解为：

(20)

式中，HCRBα为NLM×NLM的矩阵；HCRBθ为常量，二者分别表示α和θ的MSE下界。通过求取混合信息矩阵(Hybrid Information Matrix，HIM)的逆就可以得到HCRB，HIM可以表示为：

(21)

式中，p(α|θ)为先验分布；Γ(α，θ)为FIM，可以表示为：

(22)

α和θ是非相关的，因此p(α|θ)=p(α)，则Λ(θ)中的第2项可以表示为：

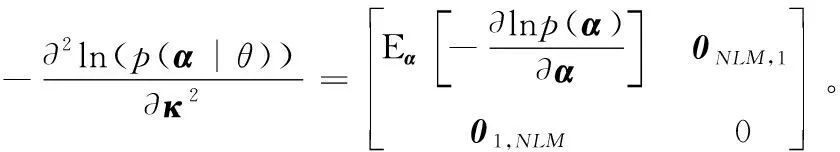
(23)

4 仿真分析

下面对所提方法进行仿真分析，并与传统的信道估计方法进行了对比。BEM模型基函数的个数为6，仿真参数如表1所示。CFO在传输数据块内是假设不变的，归一化CFO数值设为0.3。考察对本文所提方法在不同导频数量条件下的归一化均方误差(Normalized Mean Square Error，NMSE)和误比特率(Bit Error Rate，BER)性能。

表1 仿真参数

CFO和信道估计的NMSE随SNR的变化情况如图1所示。

图1 参数估计NMSE随SNR的变化曲线

由图1可以看出，CFO和信道估计的NMSE随着SNR的增大而降低。由于在计算HCRB时采用的是基于信道统计数据的HIM，因此CFO估计的NMSE没有十分接近HCRB。采用本文方法的系统BER性能如图2所示，当SNR合适时，完全可以满足系统通信需求。可见所提方法能够有效提升估计性能，并且BEM模型中待估计的基数量也远远小于估计信道各径增益的数量，能够降低运算的复杂度。

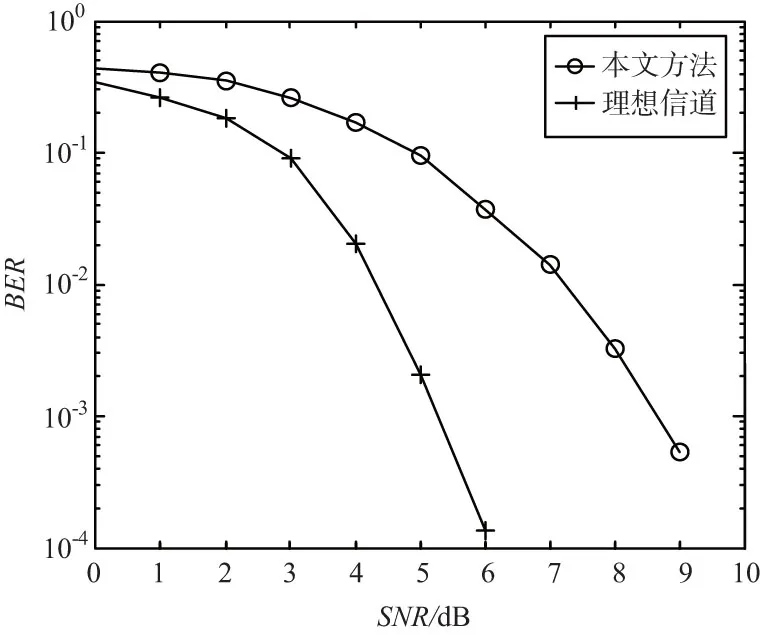
图2 系统BER随SNR的变化曲线

5 结束语

本文针对快速时变信道条件下的OQAM/OFDM中CFO和信道联合估计问题，为了避免快速时变信道中待估计参数过多，将物理信道参数建模为BEM模型，利用EM算法对频偏和快速时变的信道进行了联合估计，并分析了估计方法的HCRB。本文方法能够减少计算复杂度，提升估计精度，通过仿真实验验证了所提方法的优越性。针对不同信道条件下的联合估计问题，将是下一步研究的重点。