机械工程控制基础与MATLAB的融合

王秀玲 何秀媛 卜玮晶

摘 要：機械工程控制基础这门课程对于学生来说，比较难学、难懂，在课程教学中结合MATLAB进行融合，可以使计算容易化、框图运算通用化、时域分析直观化、频域分析通俗化、稳定性判定数字化。

关键词：机械工程控制基础;MATLAB;融合

《机械工程控制基础》是机械各专业的一门比较重要的专业基础课程，本课程主要讲述系统、输入、输出三者之间的动态关系，对已知的系统输入已知的信号，求出输出，通过输入来评定系统的稳定性、快速性、准确性。在该门课程的教学中，如果只单单结合课本，结合PPT进行讲解，学生难以理解，难于学会。因此在该课程的教学中，与MATLAB深入的融入，使得计算容易化、框图运算通用化、时域分析直观化、频域分析通俗化、稳定性判定数字化。

一、计算容易化

该课程中通过建立系统、输入、输出三者之间关系微分方程的数学模型，求出输出，通过输出来评定系统特性。对于微分方程的求解，尤其高阶微分方程求解更是困难。在此引入了拉普拉斯变换和拉普拉斯反变换，使得微分方程的求解变得比较容易。对于比较简单的拉氏变换和反变换通过常用的变换定理可以计算出来，对于比较复杂的就难于计算。与MATLAB结合后，此部分就变得非常简单，常用拉氏变换的函数命令格式：F=laplace（f）;拉氏反变换的函数命令格式 f=ilaplace（F） 。

二、框图运算通用化

系统方框图的结合MATLAB求解，更加通俗例如：

syms G1 G2 H

A=[ 0，-G1，0;G2，0，-G2;0，H，0];

b=[ G1;G2;0];c=[0，1，0];

Y2Ua=c*（（eye（size（A））-A）＼b）

得出结果如下：

Y2Ua =

（G2*（G1 + 1））/（G1*G2 + G2*H + 1）

三、时域分析直观化

在时域分析中，就是对于已经的系统输入已知的信号，求出输出，通过输出研究系统特性，结合MATLAB很容易地画出输出曲线，使得分析直观化。

例如：已知系统传递函数为G（S）=2/（s^2+s+2），求单位脉冲信号作用下的输出。

>> num=;den=[1，1，2];

Gs=tf（num，den）;

impulse（Gs）

四、频域分析通俗化

本课程在频域分析方面就是通过频率特性曲线，判断闭环系统的稳定性和

稳定裕量。本部分难点就是绘制Bode图和nyquist图，与MATLAB结合后，频域分析中绘图就更加简单更加通俗化，很容易实现。

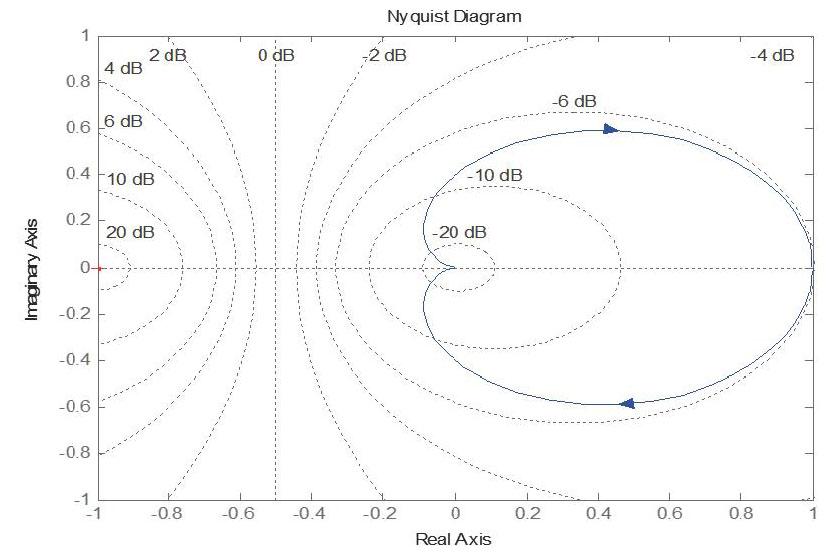
例如：试绘制G（s）=1/（8s+1）（2s+1）的Nyquist曲线。

num=;den=conv（[8 1]，[21]）;

nyquist（num，den）

五、稳定性判定数字化

系统稳定的充分必要条件是：闭环系统的特征方程的全部根具有负实部。关键在于求出特征方程的根。

例如：已知系统的传递函数为

试判定系统的稳定性。

MATLAB 程序如下：

>> num=[1];den=[2，3，1，5，4];

G=tf（num，den）;[p，z]=pzmap（G）

p =

0.4764 + 1.1405i

0.4764- 1.1405i

-1.6679 + 0.0000i

-0.7849 + 0.0000i

z =

Empty matrix：0-by-1

从上面结果可以看出特征方程具有正实部的根，因此系统不稳定

参考文献

[1] 董玉红.机械控制工程基础[M].机械工业出版社，2013，5.

[2] 刘超.自动控制原理的MATLAB仿真与实践[M].机械工业出版社，2015.4.