SV波斜入射形成的动应力路径及影响因素分析
2018-02-10李琪群凌道盛
黄 博, 李琪群,3, 凌道盛, 王 宇
(1.浙江大学 建筑工程学院岩土工程研究所,杭州 310058; 2.浙江大学 软弱土与环境土工教育部重点实验室,杭州 310058;3.中交第四航务工程勘察设计院有限公司,广州 510230)
场地土体是地震灾变传播的媒介和承灾体。一般认为,地震的破坏作用主要是由基岩竖直向上传播的剪切波引起的。基于这种认识,对土体在地震作用下动力响应的研究,多采用Seed等[1-4]提出的简化方法,通过动单剪或动三轴仪在试样上施加等效振次的正弦波,模拟垂直入射时SV波在土单元体上产生的水平往复剪应力作用。
随着土工仪器功能的进步,研究地震波的随机性、多向性等特征下的土体动力响应特性成为可能。Ishihara等[5]将不规则地震波分为冲击型波和振动型波,通过动三轴试验证实两种类型地震波对饱和砂土液化特性影响显著;袁晓铭等[6-7]进一步通过室内动力试验、有限元数值方法研究了地震波加载次序、不对称性、加载方向、地震波类型、加载维数等,发现这些因素对土体动力变形的影响非常显著。在较早研究地震多向性对土体动力特性影响的学者中,Ishihara等[8]利用动单剪仪对饱和砂土进行了不同相位差下的双向动剪切试验,试验显示双向振动时砂土的动强度更低;Pyke等[9]进行的干砂单、双及三向振动试验表明多向振动的震陷量更大;谷川等[10]利用变围压动三轴试验模拟了垂直入射的P波和SV波的耦合作用。研究表明多向振动下土体的动强度要比单向振动时下降20%~30%,超静孔压的累积速率明显加快,变形增大,更易发生液化。
上述研究着重考虑的影响因素虽有所不同,但均基于地震波垂直入射假定。实际上,在大多数情况下地震为斜入射。Jin等[11]通过1933~1980年美国214个地震动记录,分析得出一般基岩场地的地震波入射角大致为45°~75°,平均入射角和标准差为56.78°±6.77°;Takahiro等[16]根据日本24个强震记录反演得出地震波近地表处的入射角平均值为38°,变化范围为12.4°~54.1°。
土的动力特性与其动应力路径有关。通过针对饱和砂土的动力空心圆柱扭剪试验,丁浩等[12]指出圆形、椭圆形应力路径下的不排水动强度低于循环扭剪和循环三轴。交通[14]与波浪荷载[15]等动载形成的复杂应力路径对土体动力特性影响也非常显著。

对SV波斜入射下动应力路径变化规律的研究,是进行地震作用下土体动力特性研究的基础,对深入了解土体动应变、动孔压、动强度的变化发展规律具有重要意义。基于弹性波动理论,本文分析了SV波斜入射在场地中形成的动应力路径形式,特别讨论了SV波入射角大于临界角的特殊情况。在此基础上,分析了入射角、土体泊松比、单位波长深度等因素对动应力路径形状和大小的影响;并将本文方法与Seed给出的SV波垂直入射时产生的地震剪应力进行了对比。
1 斜入射SV波形成的应力路径
1.1 入射角小于临界角情况
基于弹性波动理论,P波和SV波斜入射在半无限空间的自由表面形成反射,地基土中任一点地震波引起的动应力是入射和反射波场的叠加。但不同的是,SV波斜入射存在一个临界入射角,临界角γc可由下式计算:
(1)
式中:vs为SV波波速;vp为P波波速;μ为土体泊松比。
当γ<γc时,入射SV波将产生反射SV波和反射P波。建立平面直角坐标系xoz,如图1(a)所示,与P波斜入射时情况类似,入射和反射SV波的势函数可表示为式(2)、(3)形式:
ψ-=B-exp[ik1(xsinγ-zcosγ-vst)]
(2)
ψ+=B+exp[ik2(xsinβ+zcosβ-vst)]
(3)
反射P波的势函数表示为:
φ+=A+exp[ik(xsinα+zcosα-vpt)]
(4)


(a) γ<γc

(b) γ >γc图1 斜入射地震波在自由表面的反射Fig.1 Reflection of obliquely incident seismic waves on free surface
根据Snell定律,各参数的关系可由视波数k0、视波速vo和反射介质常数K表达为:
(5)
B-、B+、A+为波幅,其相互间的比例关系可由半空间边界条件:
(6)
确定为:
(7)


图2 斜椭圆应力路径示意图Fig.2 Typical oblique elliptic stress path
1.2 入射角大于临界角情况
当SV波入射角大于临界角时,如图1(b)所示,不存在通常意义上的反射P波,即反射角α不再是一实数角。因此将入射角γ和P波反射角α的大小定义为:

(8)
式中:i为虚数单位,
(9)
(10)
将式(8)代入式(4),反射P波势函数表示为:
φ+=A+exp(-rk0z)exp[ik0(x-v0t)]
(11)
式中:反射P波的波幅A+exp(-rk0z)是随深度z呈指数减小的函数,这反映了反射P波的面波特性。
类似地,将式(8)分别代入式(2)、(3),整理得入射、反射SV波的势函数:
ψ-=B-exp[ik0(x-v0t)-ik0sz]
(12)
ψ+=B+exp[ik0(x-v0t)+ik0sz]
(13)
根据边界条件(6),推得反射P波、反射SV波与入射SV波的幅值比表达式为:
(14)
式中:
(15)
(16)

(17)
式中: 系数M1、M2、N1、N2均与ξ无关,分别为:
(18)
若将式(17)视为ξ的参数方程,且有M1N1+M2N2≡0,利用消去法与三角函数关系sin2ξ+cos2ξ=1可推得:
(19)

至此,从数学上证明了斜入射角γ>γc的SV波产生的动应力路径在无量纲双剪应力平面内的轨迹亦为斜椭圆。以rx、ry分别表示椭圆在双剪应力X,Y方向上的半径长:
(20)

图3 γ>γc时形成的正椭圆应力路径Fig.3 Induced positive elliptic stress path when γ>γc


(21)
描述椭圆的形状。该比值可以直观反映两个剪应力分量的比例。图4给出了ry/rx<1、ry/rx=1、ry/rx>1三种情况下的椭圆形状。取椭圆中较大的半径max{rx,ry}描述椭圆的大小,可以反映地震动应力水平。

图4 不同ry/rx下应力路径形状Fig.4 Ellipse stress paths under different ry/rx
2 动应力路径形状分析
对式(20)、(21)以及式A-Ⅱ-(12)~ (14)的进一步分析可以发现,影响SV波斜入射产生的斜椭圆形动应力路径的参量有入射角γ、泊松比μ和单位波长深度zf/vs。根据Yang等[20]对土体饱和度与泊松比的分析,本文泊松比μ考虑0.3,0.4,0.48三种情况,分别代表土体中等饱和、近似饱和完全饱和三种状态。取浅层地基为研究对象,单位波长深度zf/vs变化范围为0~0.5。
2.1 入射角小于临界角情况
图5给出了根据式(1)绘制的SV波临界角与土体泊松比的关系曲线,土体越接近饱和,临界角越小。当μ为0.3,0.4,0.48时,对应临界角分别为11.31°、24.09°和32.30°。

图5 SV波临界角随泊松比变化曲线Fig.5 Curve of SV-waves critical angle versus Poisson’s ratio
图6给出μ=0.4,γ= 10°时斜椭圆路径倾角θ和短长轴比δ随zf/vs的变化曲线以及代表性点对应的应力路径形状示意。图中曲线可分为三个变化阶段。第Ⅰ段θ从0急剧增大到接近90°,δ从0呈线性增大到接近1,表明斜椭圆由扁平状逐渐向正圆形变化,如图中A到B点。第Ⅱ段占整条曲线的绝大部分,θ保持或接近90°,而δ经历了从极大值(B点)降低到0(D点) 再逐渐增大至另一个极值(F点)的变化,这表明Ⅱ段应力路径是长轴在Y轴附近而扁平率不断变化的椭圆,如B~F点的应力路径形状变化。图中D点δ为0,表示动应力仅有水平剪应力分量,没有偏差正应力分量。第Ⅲ段斜椭圆变化趋势则与第Ⅰ段相反,如F~G点应力路径所示。
图7给出了入射角γ=10°时,不同泊松比下椭圆路径θ和δ随zf/vs的变化曲线,图8给出了μ=0.4时,不同入射角下椭圆路径θ和δ随zf/vs的变化。可见,小于临界角时,θ或δ随zf/vs的变化仍呈三个发展阶段。随入射角从1° 增大至20°,Ⅱ区间范围缩小了36.6%,倾角θ的最大值有一定降低,但变化很小,仅3.8°;当泊松比从0.3变化至0.48,对Ⅱ区间范围和倾角最大值均影响不大。在更接近地表的Ⅰ区间,入射角和泊松比的增大均使得斜椭圆形状向水平剪应力分量占比减小的方向发展。
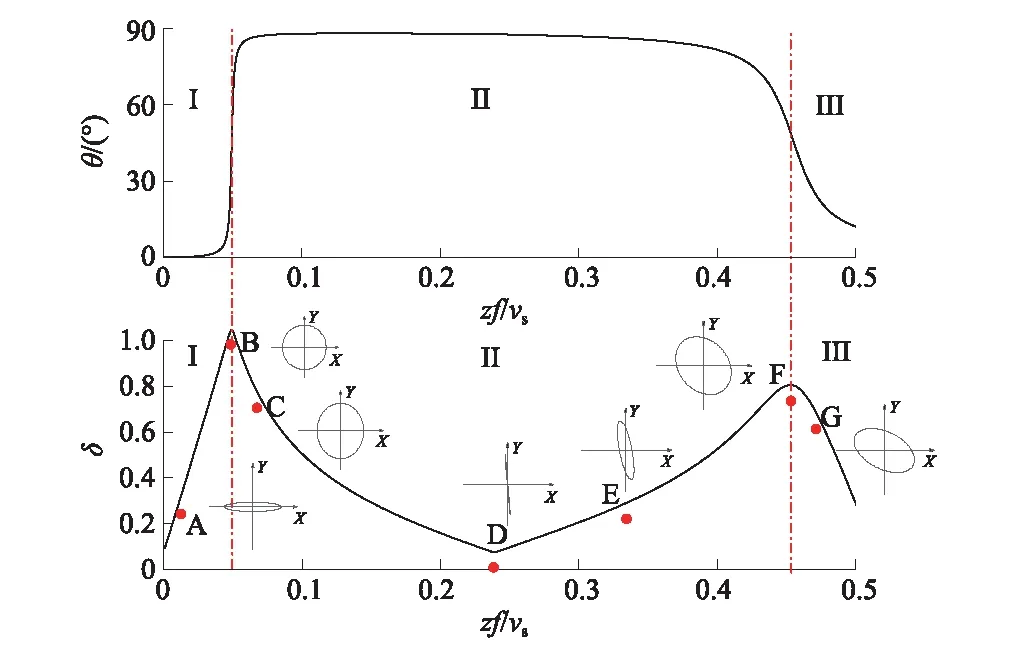
图6 当γ=10°且μ=0.4时,θ和δ随z f/vs变化曲线Fig.6 θ and δ develop with z f/vs when γ=10° and μ= 0.4

图7 当γ=10°时,不同泊松比下θ和δ随z f/vs变化曲线Fig.7 θ and δ develop with z f/vs varying at different Poisson’s ratio when γ=10°
2.2 入射角大于临界角情况
γ>γc时,形成的动应力路径均为正椭圆,仅需考察ry/rx的变化即可确定椭圆形状。图9给出了ry/rx随zf/vs的典型变化模式(γ=10°,μ=0.4)。曲线的变化趋势可大致分为两段,第Ⅰ段ry/rx从0单调急剧增大至∞,由扁平椭圆变为竖直椭圆,如图中A、B点,剪应力中偏差正应力分量所占比例不断减小,而水平剪应力分量比例逐步增大;第Ⅱ段ry/rx从∞减小至0,椭圆路径经历了如图B,C,D点的形状变化,剪应力中两个分量的占比变化恰与第Ⅰ段相反。其中,C点应力路径为圆形、D点应力路径为直线,可视为椭圆的特殊情况。在D点之后,ry/rx的变化周期性重复第Ⅰ、Ⅱ段的变化模式,此处不作赘述。

图8 当μ=0.4时,不同入射角下θ和δ随z f/vs变化曲线Fig.8 θ and δ develop with z f/vs varying at different incident angle when μ= 0.4

图9 当γ=60°且μ=0.4时,ry /rx随z f/vs变化曲线Fig.9 ry/rx develops with z f/vs when γ=60° and μ= 0.4
图10给出了μ=0.4时,不同入射角下ry/rx随zf/vs的变化。不同入射角下椭圆路径也如图9所示分成典型的两阶段变化。在μ=0.4下,随入射角度从50°增大至89°,Ⅰ、Ⅱ段的横坐标分界点zf/vs从0.031增大至0.106,ry/rx=0对应的D点出现位置也随之增大了0.247。以入射角45°为界,45°以下至临界角也有上述类似的规律,但其曲线段Ⅰ相比入射角50°以上时占据范围更大。以30°为例,在本文考虑的zf/vs变化范围0~0.5,几乎均为区段Ⅰ占据。宏观上,入射角增大使得处于区段Ⅰ的椭圆路径朝水平剪应力分量占比减小的方向发展,区段Ⅱ反之。

图10 当μ=0.4时,不同入射角下ry/rx随z f/vs变化曲线Fig.10 ry /rx develops with z f/vs varying at different incident angle when μ= 0.4
入射角为45°是一特殊情况,如图11(a)所示,此时半空间中不发生波型的转换,即不产生反射P波,与此对应的rx、ry变化如图11(b)所示,ry恒为0,即剪应力中只存在偏差正应力分量,其应力路径与图9中D点一致。

(a) 45°入射角在半空间中的反射情况

(b) 剪应力分量变化曲线图11 45°入射角在半空间中特殊反射情况下的剪应力分量Fig.11 Special reflection and shear stress components with 45° incident angle in semi-infinite space
以γ= 60°为参考,图12中给出了不同泊松比时ry/rx随zf/vs的变化曲线。在本文的zf/vs考察范围内,泊松比μ对应力路径形状影响很小,对Ⅰ区段无影响,在Ⅱ区段,随μ增大ry/rx稍有增加,即水平剪应力分量占比有一定增大。

图12 当γ=60°时,不同泊松比下ry/rx随z f /vs变化曲线Fig.12 ry/rx develops with z f/vs varying at different Poisson’s ratio when γ= 60°
3 动偏应力幅分析
在多向振动时,通常以偏应力来衡量动应力的大小[21],定义如下:
(22)

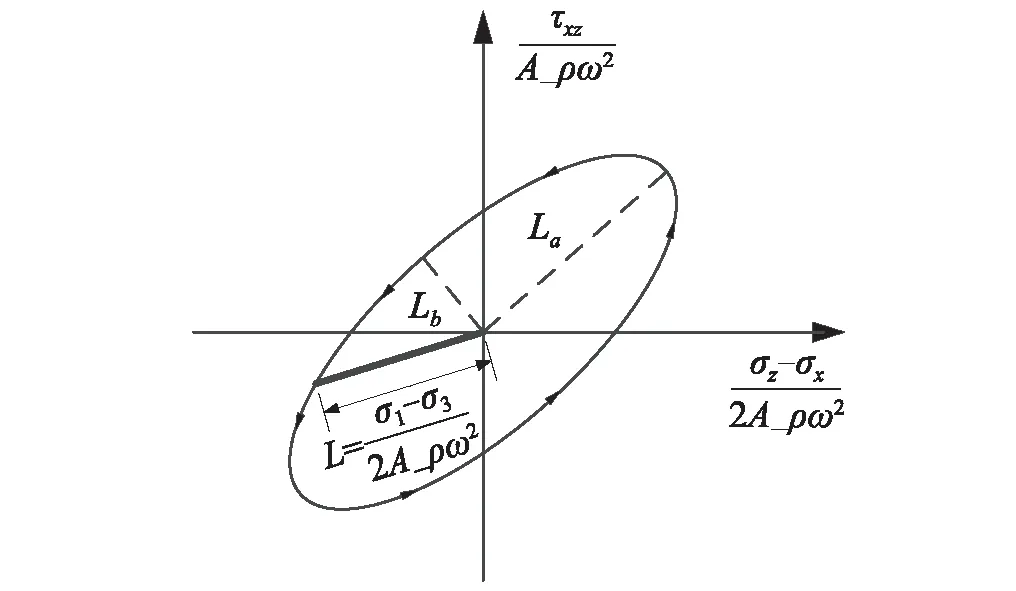
图13 斜椭圆应力路径的偏应力Fig.13 Deviator stress of obliquely elliptic stress path
3.1 入射角小于临界角情况
如图14所示,μ=0.4时,γ<γc下斜椭圆路径长半轴长La随zf/vs的变化可概括为“稳-抛-稳”,即中间段类似抛物线形,在本文的所取参数变化范围内,La最大值为2左右。无量纲量zf/vs也可视为无量纲频率,图14中La达到峰值对应的最小zf/vs值为土体一阶固有频率,大致为0.25。由于土体阻尼的存在,相比于二阶及其后的高阶固有频率,一阶固有频率对应的动应力幅值通常最大。结合图7,一阶固频内的动应力主要是水平剪应力分量。随入射角增大,一阶固有频率略有增加,而最大动应力水平稍有降低。μ对动偏应力幅影响普遍较小,曲线差别不大,不再一一给出图形。
值得指出的是,在曲线起始段La并未从0开始,而是存在幅值几乎不变的稳定区,在该区域内La变化很小。结合图7,地表浅层平稳段对应于δ曲线的第Ⅰ段,动应力以偏差正应力分量为主。说明偏差正应力受zf/vs影响较小。但该段随入射角增加La提升明显,是近垂直入射的十数倍。在曲线末段同样也存在类似的幅值稳定区,考虑到半波长深度土体自重应力也随之增大,同样的动应力水平下,地表浅层区域动应力比更大,因此更为危险。

图14 当μ=0.4时,不同入射角下La随z f /vs变化曲线(γ<γc)Fig.14 La develops with z f/vs varying at different incident angle when μ= 0.4
3.2 入射角大于临界角情况
图15给出了μ=0.4时,γ>γc下max{rx,ry}随zf/vs的变化。在本文研究的参数变化范围内,曲线表现为明显的“降-稳-抛”三段式,即起始段随zf/vs增大呈线性下降,中间段随zf/vs稍有增大,这两段仅占整条曲线的很小部分。起始段max{rx,ry}减小是由于近地表处P波波幅的迅速衰减所致,结合图10,此时的动应力以偏差正应力分量为主。说明偏差正应力反而受zf/vs影响明显,不同于γ<γc的情况。第三段呈抛物线,不仅占整条曲线的绝大部分,且max{rx,ry}变化幅度也最大,同样的,在本文的所取参数变化范围内max{rx,ry}峰值在2左右。随着入射角度增大max{rx,ry}峰值下降,当入射角度为80°~90°,即近水平入射时,在半波长深度范围内max{rx,ry}不超过0.5,动应力水平整体较低。
入射角为45°的特殊情况,从图11(b)的rx,ry曲线变化表明此时仅有剪应力分量τxz,即max{rx,ry}=ry,其随无量纲深度呈抛物线变化如ry曲线。相近角度下具有类似的特性,如40°情况下的曲线与γ<γc情况相似,泊松比的变化对动剪应力水平影响很小。限于篇幅,不一一给出相应曲线。

图15 当μ=0.4时,不同入射角下La随z f/vs变化曲线(γ>γc)Fig.15 La develops with z f/vs varying at different incident angle when μ= 0.4
3.3 与Seed方法计算的地震剪应力比较
Seed-Idriss[4]对垂直向入射SV波采用下式计算地震峰值动剪应力:
(23)
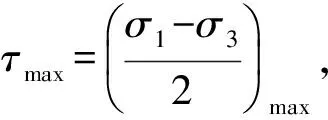
黄博等[17]将入射波频率1 Hz,泊松比0.42等参数值代入,比较了7度地震(地表峰值加速度0.1 g)时,采用本文方法和Seed方法计算的SV波垂直入射产生的地震动剪应力。结果表明:对于密度1 800 kg/m3的土体,将剪切波速取300 m/s以上便可视为Seed-Idriss假定的刚性地基,将剪切波速取80 m/s左右便与刚度修正结果基本吻合,能反映浅层土体的平均刚度。这也从侧面说明本文方法的正确性。
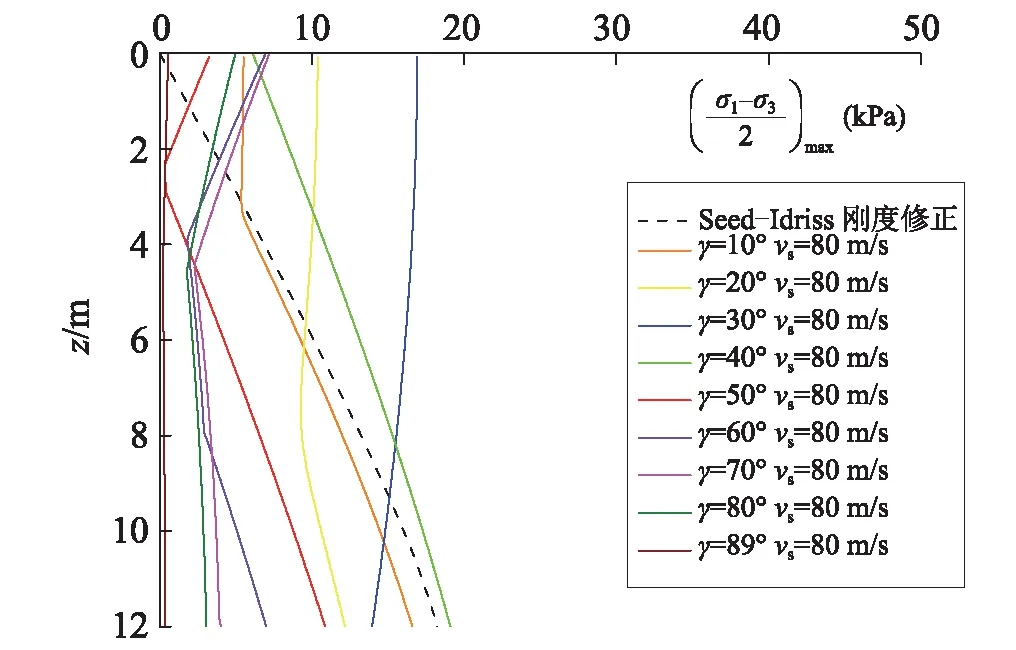
为比较斜入射SV波引起的地震动应力大小,图16给出了土体泊松比为0.3、0.4、0.48,质量密度1 800 kg/m3、剪切波速80 m/s时,SV波不同角度入射时峰值动偏应力幅随深度的关系曲线,其中斜入射波的波幅、波频同黄博等研究保持一致。图中,Seed-Idriss修正刚度法足够将大部分工况下的最大动偏应力包括在内,但在入射角度20°~40°之间,12 m深度以内的浅层地基出现无法包络在内的更不利情况,动应力大于其它情况,是危险的入射角范围。当泊松比取值为0.4时,30°入射角产生的动偏应力最大,分别是泊松比0.3、0.48时的1.3倍~1.9倍和1.04倍~1.15倍。基于上述结果可初步推断,近似饱和的地基在SV波30°左右斜入射工况下最为危险。
(a) μ= 0.3

(b) μ= 0.4
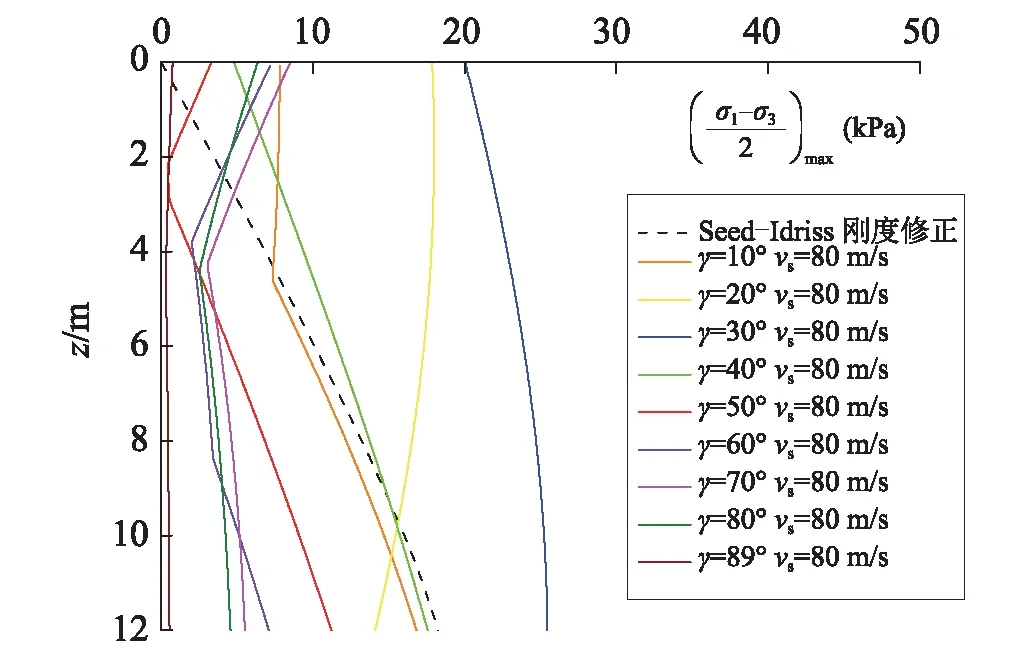
(c) μ= 0.48图16 不同入射角度、泊松比下动偏应力幅值随深度的变化Fig.16 Dynamic deviatoric stress amplitude varies with depth under different incident angle and Poisson’s ratio
4 结 论
SV波存在一个临界角,这使得斜入射SV波形成的应力路径在入射角大于和小于临界角时具有不同特征。当入射角小于临界角时,单位波长深度范围内应力路径以竖直扁椭圆形式为主,水平剪应力分量是主要的剪应力形式,当入射角大于临界角时,则多为以偏差正应力为主的水平扁椭圆形式。
椭圆路径的长半轴长La或max{rx,ry} 是SV波产生的动偏应力幅,代表了地震波引起的动应力水平,受泊松比的影响较小。当入射角小于临界角时,0.25的单位波长深度下应力水平最高,长半轴达到2左右。入射角大于临界角后,由于反射P波以面波形式存在,浅层区域延深度方向有明显的动应力衰减迹象。至近水平入射,长半轴的值普遍低于0.5。近饱和的地基在斜入射角为20°~40°之间产生的动应力最大,且此时斜入射形成的动应力比传统的Seed-Idriss计算方法得到的结果更大,最为危险。
可见,斜入射条件下,SV波引起的动应力路径形式多变,动应力水平有可能更高。仅考虑地震波垂直入射还不足以涵盖最危险的震灾工况,对SV波斜入射条件下土体的动应力响应研究很有必要。
[ 1 ] SEED H B, LEE K L. Liquefaction of saturated sands during cyclic loading[J]. Journal of Soil Mechanics and Foundations Division, ASCE, 1966, 92(6): 105-134.
[ 2 ] THIERS G R, SEED H B. Cyclic stress-strain characteristics of clays[J]. Journal of Soil Mechanics and Foundations, 1968, 94(2): 555-569.
[ 3 ] SEED H B, PEACOCK W H. Test procedures for measuring soil liquefaction characteristics[J]. Journal of the Soil Mechanics and Foundation Division, ASCE, 1971, 97(8): 1099-1119.
[ 4 ] SEED H B, IDRISS I M. Simplified procedure for evaluating soil liquefaction potential[J]. Journal of Soil Mechanics and Foundation Division, ASCE, 1971, 97(9): 1249-1273.
[ 5 ] ISHIHARA K, YASUDA S. Sand liquefaction under random earthquake loading condition[C]∥Proceedings of the 5th World Conference on Earthquake Engineering. Rome: ASCE. 1973: 329-338.
[ 6 ] 袁晓铭, 孙锐, 孟上九. 土体地震大变形分析中 Seed 有效循环次数方法的局限性[J]. 岩土工程学报, 2004, 26(2): 207-211.
YUAN Xiaoming, SUN Rui, MENG Shangjiu. Limitation of the Seed’s method of significant cyclic number in analyzing large deformation of soils during earthquake[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(2): 207-211.
[ 7 ] 陈青生, 高广运, 何俊锋. 地震荷载不规则性对砂土震陷的影响[J]. 岩土力学, 2011, 32(12): 3713-3720.
CHEN Qingsheng, GAO Guangyun, HE Junfeng. Effect of irregularity of earthquake loading on seismic compression of sand[J]. Rock and Soil Mechanics, 2011, 32(12): 3713-3720.
[ 8 ] ISHIHARA K, YAMAZAKI F. Cyclic simple shear tests on saturated sand in multi-directional loading[J].Soils and Foundatinos,1980, 20(1):45-59.
[ 9 ] PYKE R M, CHAN C K, SEED H B. Settlement of sands under multidirectional shaking[J]. Journal of the Geotechnical Engineering Division, 1975, 101(4): 379-398.
[10] 谷川, 蔡袁强, 王军. 地震 P 波和 S 波耦合的变围压动三轴试验模拟[J]. 岩土工程学报, 2012, 34(10): 1903-1909.
GU Chuan, CAI Yuanqiang, WANG Jun. Coupling effects of P-waves and S-waves based on cyclic triaxial tests with cyclic confining pressure[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(10): 1903-1909.
[11] JIN X, LIAO Z. Statistical research on S-wave incident angle[J]. Earthquake Research in China,1994, 8(1): 121-131.
[12] 丁浩. 地震波作用下饱和砂土动力特性试验研究[D]. 杭州: 浙江大学, 2010.
[13] 李男, 黄博, 凌道盛, 等. 斜椭圆应力路径下饱和松砂动力特性试验研究[J]. 岩土力学, 2015, 36(1): 156-170.
LI Nan, HUANG Bo, LING Daosheng, et al. Experimental research on behaviors of saturated loose sand subjected to oblique ellipse stress path[J]. Roch and Soil Mechanics, 2015, 36(1): 156-170.
[14] 钱建固, 王永刚, 张甲峰, 等. 交通动载下饱和软黏土累计变形的不排水循环扭剪试验[J]. 岩土工程学报, 2013, 35(10): 1790-1798.
QIAN Jiangu, WANG Yonggang, ZHANG Jiafeng, et al. Undrained cyclic torsion shear tests on permanent deformation responses of soft saturated clay to traffic loadings[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1790-1798.
[15] 栾茂田, 聂影, 杨庆, 等. 不同应力路径下饱和黏土耦合循环剪切特性[J]. 岩土力学, 2009, 30(7): 1927-1932.
LUAN Maotian, NIE Ying, YANG Qing, et al. Study of coupling cyclic test of saturated clay under different stress paths[J]. Rock and Soil Mechanics, 2009, 30(7): 1927-1932.
[16] TAKAHIRO S, KAZUHIKO K, et al. Estimation of earthquake motion incident angle at rock site[C]∥ Proceedings of 12th World Conference on Earthquake Engineering.[S.l.]:[s.n.], 2000, 0956.
[17] 黄博, 凌道盛, 丁浩, 等. 斜入射地震波在土体中产生的动应力路径及试验模拟[J]. 岩土工程学报, 2013, 35(2): 276-283.
HUANG Bo, LING Daosheng, DING hao, et al. Seismic stress path induced by obliquely incident waves and its simulation [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 276-283.
[18] 徐仲达. 地震波理论[M]. 上海: 同济大学出版社, 1997.
[19] PUJOL J. Elastic wave propagation and generation in seismology[M]. Cambridge University Press, 2003.
[20] YANF J, SATO T. Interpretation of seismic vertical amplification observed at an array site[J]. Bulletin of the Seismological Society of America, 2000, 90(2): 275-285.
[21] ISHIHARA K J. Soil behaviour in earthquake geotechnics[M]. Oxford University Press, 1996.
[22] ISHIHARA K, TOWHATA I. Sand response to cyclic rotation of principal stress directions as induced by wave loads [J]. Soils & Foundations, 1983, 23(4): 11-26.
附录
Ⅰ单一SV波小于临界角斜入射产生的地震动应力路径形式


A-1-(1)
式中:M1、M2、N1、N2具体表达式如下,
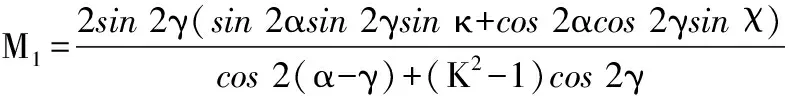
A-Ⅰ-(2)
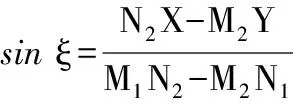

A-Ⅰ-(3)
对比斜椭圆方程的一般形式及条件:
Ax2+By2+2Cxy=1(C2-AB<0)
A-Ⅰ-(4)

Ⅱ小于临界角动应力路径特征参数解析表达式
数学上,斜椭圆的解析表达式可表示成由几何参数构成的形式:
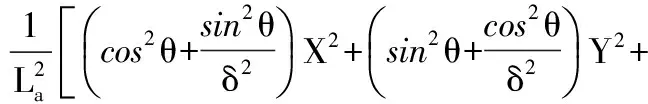
A-Ⅱ-(1)
如图2所示,2La表示斜椭圆长轴长,2Lb表示斜椭圆短轴长。θ表示斜椭圆的倾斜角(长轴与X正半轴夹角,逆时针为正),反映了椭圆的倾斜程度。短长轴之比δ=Lb/La也称为椭圆率,反映椭圆扁平程度。A-Ⅱ-(1)式中中括号内的式子代表长半轴长为 1 的单位斜椭圆。因此θ、δ和La三个参数是斜椭圆的特征参数。
将式A-Ⅰ-(3)整理为式A-Ⅱ-(1)形式,从而得到SV波斜入射形成的无量纲斜椭圆应力路径的特征参数表达式。该特征参数的表达式和具体推导过程如下:
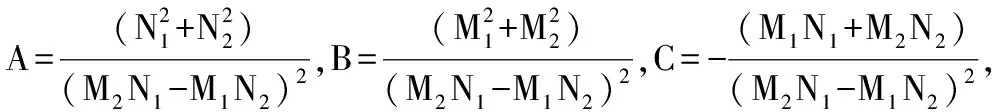
AX2+BY2+2CXY=1
A-Ⅱ-(2)


A-Ⅱ-(3)
A-Ⅱ-(4a)
A-Ⅱ-(4b)
A-Ⅱ-(4c)
分析并联立上述结果得:
A-Ⅱ-(5a)
A-Ⅱ-(5b)
A-Ⅱ-(6)
A-Ⅱ-(7)
A-Ⅱ-(8)
得到上述参数关系后,利用式A-Ⅰ-(2)继而推导A,B,C的解析表达式如下:

A-Ⅱ-(9)

A-Ⅱ-(10)

A-Ⅱ-(11)
再利用A-Ⅱ-(5)~A-Ⅱ-(8)的关系式,可以最终推导出斜椭圆特征参数的解析表达式如下:

A-Ⅱ-(12a)
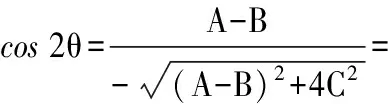
A-Ⅱ-(12b)

A-Ⅱ-(13)

A-Ⅱ-(14)
Ⅲ符号表
x为半空间中水平坐标,
z为半空间中竖向坐标(深度),
σx为水平动正应力,
σz为竖向动正应力,
τxz为水平动剪应力,
τmax为峰值水平动剪应力,
(σ1-σ3)/2为动偏应力,

X= (σz-σx)/(2A-ρω2)为无量纲偏差正应力,
Y=τxz/(A-ρω2)为无量纲水平剪应力,
α为P波反射角,
γ为SV波入(反)射角,
γc为SV波临界角,
ψ+、ψ-为SV波势函数,下标“-”指入射波,“+”指反射波,下同。
φ+为P波势函数,
B-、B+为SV波波幅,
A+为P波波幅,
k0为视波数,
k、k1、k2为波数,分别对应于反射P波、入(反)射SV波,
ω、ω1、ω2为圆频率,与波数下标相对应,
f为波频,
vp为P波波速(或压缩波波速),
vs为SV波波速(或剪切波波速),
zf/vs为单位波长深度(或无量纲频率),
ux为坐标x方向(水平向)的位移,
uz为坐标z方向(竖直向)的位移,
amax为水平向地表加速度,
g为重力加速度,
λ为拉梅常数,
G为土体剪切模量,
ρ为土体质量密度,
γs为土体容重,
μ为土体泊松比,
M1、M2、N1、N2为斜椭圆参数方程系数,
A,B,C为斜椭圆一般方程系数,
La为长半轴,
Lb为短半轴,
θ为斜椭圆倾角,
δ=Lb/La为斜椭圆短长轴比,
ry为Y方向斜椭圆半径,
rx为X方向斜椭圆半径。
