高动态下导频辅助的GNSS信号比特同步方法
2018-02-07李文刚王屹伟
李文刚, 王屹伟
(西安电子科技大学通信工程学院, 陕西 西安 710071)
0 引 言
高动态条件下,全球卫星导航系统(global navigation satellite system, GNSS)的信号将会带有较大的多频勒频率偏移,如果载体的运动具有加速度,其多普勒频率偏移也将会处于变化之中,这对于GNSS信号的处理十分不利[1-2]。在GNSS信号被捕获之后,需要对GNSS信号进行导航数据的比特同步,才能够对GNSS信号进行跟踪和解调等后续处理[3]。以北斗B1频点为例,其扩频码的周期为1 ms,中低轨道的北斗卫星数据传送速率为50 bit/s,因而每一个导航电文持续的时间为20 ms,如果捕获过程中相干累加时间为1 ms,那么存在20个可能的导航数据的比特跳变位置[4]。现代GNSS接收机比特同步过程如图1所示,将一个数据比特周期即20 ms的扩频码分为20个1 ms,即20个候选比特跳变位置,比较候选位置是否发生比特跳变,如果在该候选位置处发生比特跳变,则直方图计数加1。经过若干个数据比特周期的检测,如果直方图的峰值超过门限值,则判断该候选位置为比特跳变位置。目前的研究成果主要是基于这种方法提高其在低信噪比条件下的性能[5-7],而在高动态条件下,GNSS信号的频率会产生实时的变化,其变化的规律和载体运动的状态有关,依照传统比特同步方法和相关的改进方法,GNSS接收机无法进行稳定而可靠地进行比特同步。
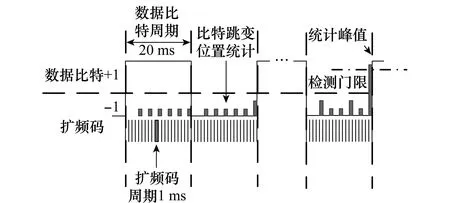
图1 传统比特同步方法Fig.1 Conventional bit synchronization method
新一代的GNSS民用信号普遍添加了正交或同向的导频信号,并将导频信号和数据信号进行了分离[8]:全球定位系统(global positioning system, GPS)的L1C、L2C、L5频点,伽利略导航系统(Galileo satellite navigation system)的E1、E5频点均采用这导频信号与数据信号分离并同步播发的形式。我国北斗导航系统的B1C、B2频点也将采用这种结构[4,6]。导频信号和数据信号的同时出现改变了GNSS接收机的结构,同时也使得GNSS信号处理的方式更加多样化:导频信号和数据信号可以以多种方式实现联合捕获[9],对导频信号和数据信号可以进行联合跟踪[10]。由于导频信号没有调制导航数据,因而不存在比特跳变,因而可以进行任意时间长度的相干累加,GNSS接收机对信号的检测方式更加灵活,对高动态和弱信号的检测更加灵敏[11]。在研究新一代GNSS信号时发现:导频信号不存在比特跳变的特性不仅仅能够延长对GNSS信号的相干累加时间,提高GNSS接收机的捕获灵敏度,这一特性同时可以用于GNSS数据信号的比特同步,尤其是在高动态条件下这一特性显得尤为重要。参考文献[12]提出并总结了“差分相干累加”的比特同步方法,然而该方法在高动态条件下不能够克服多普勒速率的影响。结合新一代GNSS信号的结构,提出一种导频辅助下的比特同步方法:将当前时刻的数据信号相干累加结果和导频信号相干累加的结果进行共轭相乘以复现当前的导航数据比特,并对结果进行相干累加和非相干累加,对可能的数据比特跳变位置处的非相干累加结果进行比较,判断比特跳变的实际位置。
1 导频辅助下的比特同步方法
新一代GNSS信号一般按照数据信号和导频信号功率1∶1或1∶3正交或同相调制而成,射频信号经过下变频成为中频信号后,对中频信号经过捕获后进行比特同步和跟踪等后续处理。
1.1 高动态条件下的中频信号捕获模型
以新体制北斗B2频点为例分析,B2频点的参数如表1所示,整个北斗B2频点属于两路交替二进制偏移载波(alternate binary offset carrier, AltBOC)[13],B2频点可以分为B2a和B2b两个信号,每一个信号可以看作正交相移键控(quadrature phase shift keying,QPSK)调制[14]。B2a以功率比为1∶1在QPSK两个正交的相位上调制数据信号和导频信号,其扩频码长度为10 230 chip、速率为10.23 Mcps、周期为1 ms。

表1 北斗B2频点调制方式
当接收机对接收到的B2a信号下变频,得到含有数据分量和导频分量的中频信号为
rIF(n)=AndncD(n-τ)cos(2π(fIF+fd)n+φn)+
AncP(n-τ)sin(2π(fIF+fd)n+φn)+ηIF(n)
(1)
式中,An为当前时刻信号幅度;dn=±1为当前时刻数据比特符号;τ为信号时延;cD(n)为数据通道扩频码和副载波乘积;fIF为中频载波频率;fd为中频载波的多普勒频偏;φn为载波相位;cP(n-τ)为导频通道扩频码和副载波乘积;ηIF(n)是均值为0的高斯白噪声。对接收信号的数据信号进行捕获,设相干累加时间为Tc=1 ms,忽略自相关函数和频率偏移对相关累加值幅度的影响,捕获后相关器输出的1 ms相干累加值为
(2)
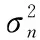
(3)
式中,f0为初始多普勒频偏,由接收机载体相对于卫星的速度引起;α为多普勒频偏速率,由接收机载体相对于卫星的加速度引起,忽略自相关函数和频率偏移对相关累加值幅度的影响,假设An=A恒定,R(Δτ)≈1,将式(3)代入式(2),得到
(4)
同理,在相同条件下,对接收信号的导频信号进行相同处理,相关器输出的1 ms相干累加值为
(5)
1.2 导频辅助下的比特同步方法
由式(4)可以看出,由载体加速度多普勒频偏速率α会导致多普勒频偏时刻变化,另外接收机载体运动状态往往具有不确定性,尤其是载体具有较大加速度情况下,此时α较大,比特同步的性能会受到严重影响。不能仅考虑消除初始速度引起的多普勒初始频偏f0对比特同步造成的影响[12]。注意到导频信号没有调制导航电文,提出利用导频信号1 ms相干累加值与数据信号1 ms的相干累加值进行实时差分的方法,即
(6)
共轭相乘的结果中第一项为信号项,其余3项为噪声项。可见第一项信号项完全不受频率偏移影响,说明共轭相乘的结果完全消除了相干累加值中频率偏移的影响,反映了当前时刻数据比特符号dn的值。设m为n之后20个可能的比特跳变位置中的某一个候选位置,分别以每一个候选位置为起点,按照式(6)对每一时刻相关器输出的1 ms输出进行处理,并将结果进行20 ms的相干累加得
(7)
当m为比特跳变位置,dn+m+l(l=0,1,2,…,19)必然同号,但是相隔20 ms的数据比特不一定变号,即m+20不一定是下一个比特跳变位置,因而有必要根据实际情况对N个比特(N×20 ms)相干累加的结果进行非相干累加得
(8)
按照式(8)经过N个比特的非相干累加,求出Rn+m,m=0,1,2,…,19中的最大值,即可估算出数据比特跳变的位置
(9)
在实际中由于噪声功率的不确定性,不能判断经过N个比特的非相干累加能够准确判断比特跳变的位置,可以定义检测量ρ,并根据ρ是否超过某一判决门限ρthres用来判断该次非相干累加后是否进行判决。定义检测量ρ为
(10)
即根据式(9)检测的出的最大相干累加结果与相邻1个候选位置处的相干累加结果进行比较,若在某次非相干累加结束后,检验出ρ≥ρthres,则对数据比特跳变位置进行判决。所提方法的示意图如图2所示。
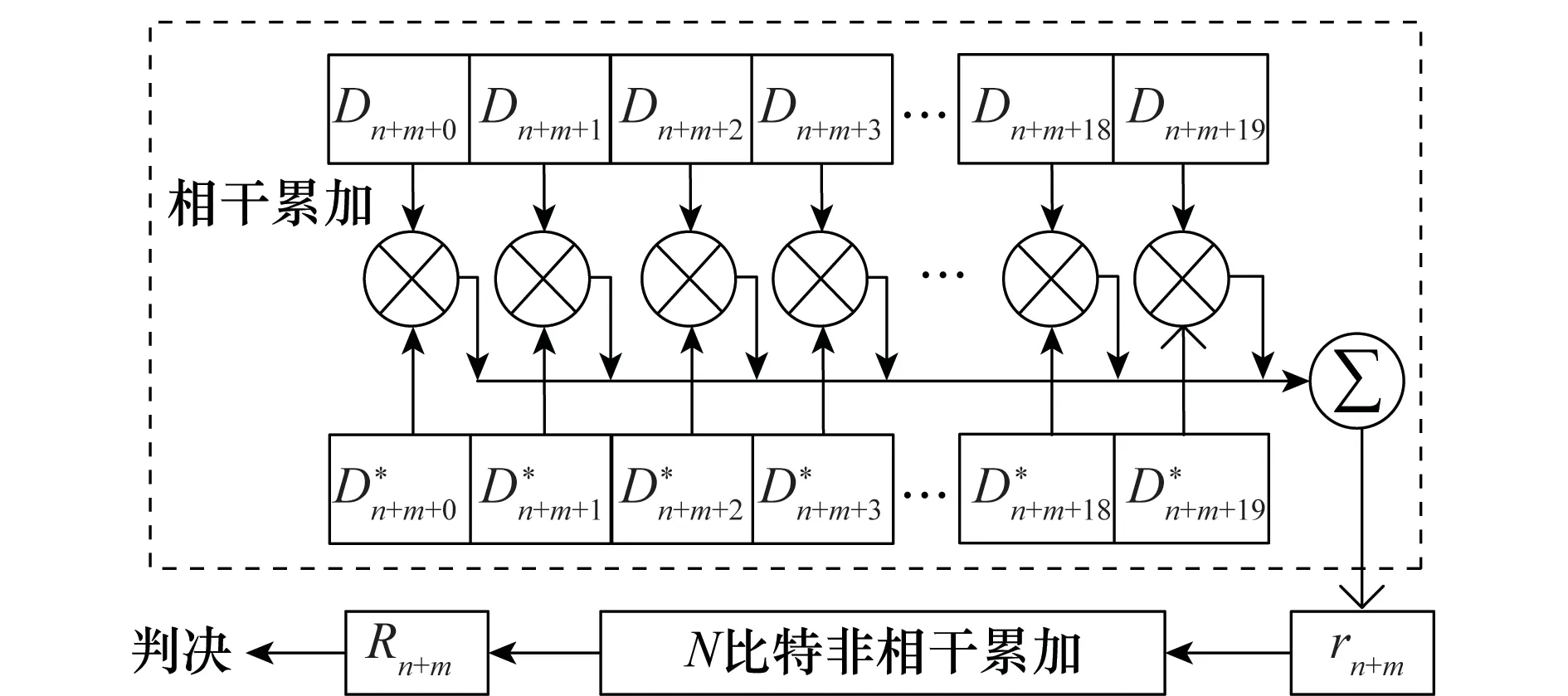
图2 所提方法示意图Fig.2 Schematic diagram of the proposed method
1.3 检测量概率分布分析
假设m为比特跳变位置,m+20亦为比特跳变时,按照式(7)进行20 ms的相干累加后即对n之后20个候选位置进行判决(即N=1的情况),注意到式(6)中前两个噪声项的二阶矩为
(11)
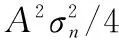
(12)
(13)
式中,K0(·)为第二类零阶修正的Bessel级数。在一定的载噪比条件下,信号的幅度和噪声功率的关系为
(14)
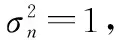
由于高斯分布的和仍然是高斯分布,高斯分布项与常量项之和包络服从莱斯分布,因而式(7)的包络近似为莱斯分布,其概率密度函数为
(15)
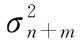
(16)
由于m为比特跳变的位置,m+20亦为比特跳变时,因而dn+m+l(l=0,1,2,…,19)同号,此时
(17)
对于m+m′(m′=1,2,3,…,19)这些不是比特跳变的位置的候选位置,由于m+20位置发生比特跳变,dn+m+m′+l(l=0,1,2,…,19)不同号,此时
(18)
根据概率密度函数(17),对其进行积分,可以求出概率分布函数
(19)
其中
(20)
称之为一阶Marcum-Q分布函数[17]。对于任何候选位置,其检测概率均服从莱斯分布,与候选位置距离实际比特跳变位置的距离md有关。
1.4 正确检测概率与错误检测概率分析
为分析所提方法的检测概率,在相隔20 ms的两个数据比特发生跳变,且对每一个比特跳变位置进行20 ms时长的相干累加的前提下,对当前检测的候选位置m进行如下对立假设:
(1) 假设H0:m是实际比特跳变的位置,m+20为下一个比特跳变的位置;
(2) 假设H1:m不是实际比特跳变的位置,实际比特跳变的位置为m+md,m+md+20为下一个比特跳变的位置。
在H0条件下判断m为实际比特跳变位置即为正确检测的概率,由于rn+m(m=0,1,2,…,19)之间相互独立,因而计算正确检测概率可以得到:
Pd=P{rn+m>rn+m+m′,m=1,2,…,19|H0}=
(21)
在H0条件下没有判断m为实际比特跳变位置为即漏检概率:
Pm=1-Pd
(22)
在H1条件下判断m为实际比特跳变位置即为虚警概率,虚警概率可以计算得到:
Pfa=P{rn+m>rn+m+m′,m=1,2,…,19|H1,md}=
(23)
对于虚警概率Pfa,其大小的不仅取决于载噪比的大小,还与该候选位置距离实际比特跳变位置的距离md有关,md越小则虚警概率越大。
2 性能测试与分析
2.1 工作特征曲线分析
在一定条件下以虚警概率为自变量、正确检测概率为因变量所绘制的曲线称为接收机的工作特征曲线,工作特征曲线能够用来评价接收机在一定条件下的工作性能。令接收机处于相对静止的情况下,载噪比C/N0分别等于35 dBHz、40 dBHz和45 dBHz,对N=1个即20 ms的数据进行观测,进行5 000次实验并统计在虚警概率Pfa一定的情况下的平均正确检测概率Pd。虚警概率与候选位置到实际比特跳变位置的距离md有关,折中考虑,仿真中取md=11。
如图3是本文所提方法的工作特征曲线。由于本文第1.4节对于所提方法性能的理论分析是近似的,因而当载噪比为35 dBHz时,理论性能与实际仿真得出的性能具有差异。当载噪比上升至40 dBHz、45 dBHz时,理论性能与实际性能的差异已经可以忽略不计,说明而理论性能与实际性能的差异随着载噪比的上升而减小,实验因而证明了本文对接收机性能的理论分析的合理性。
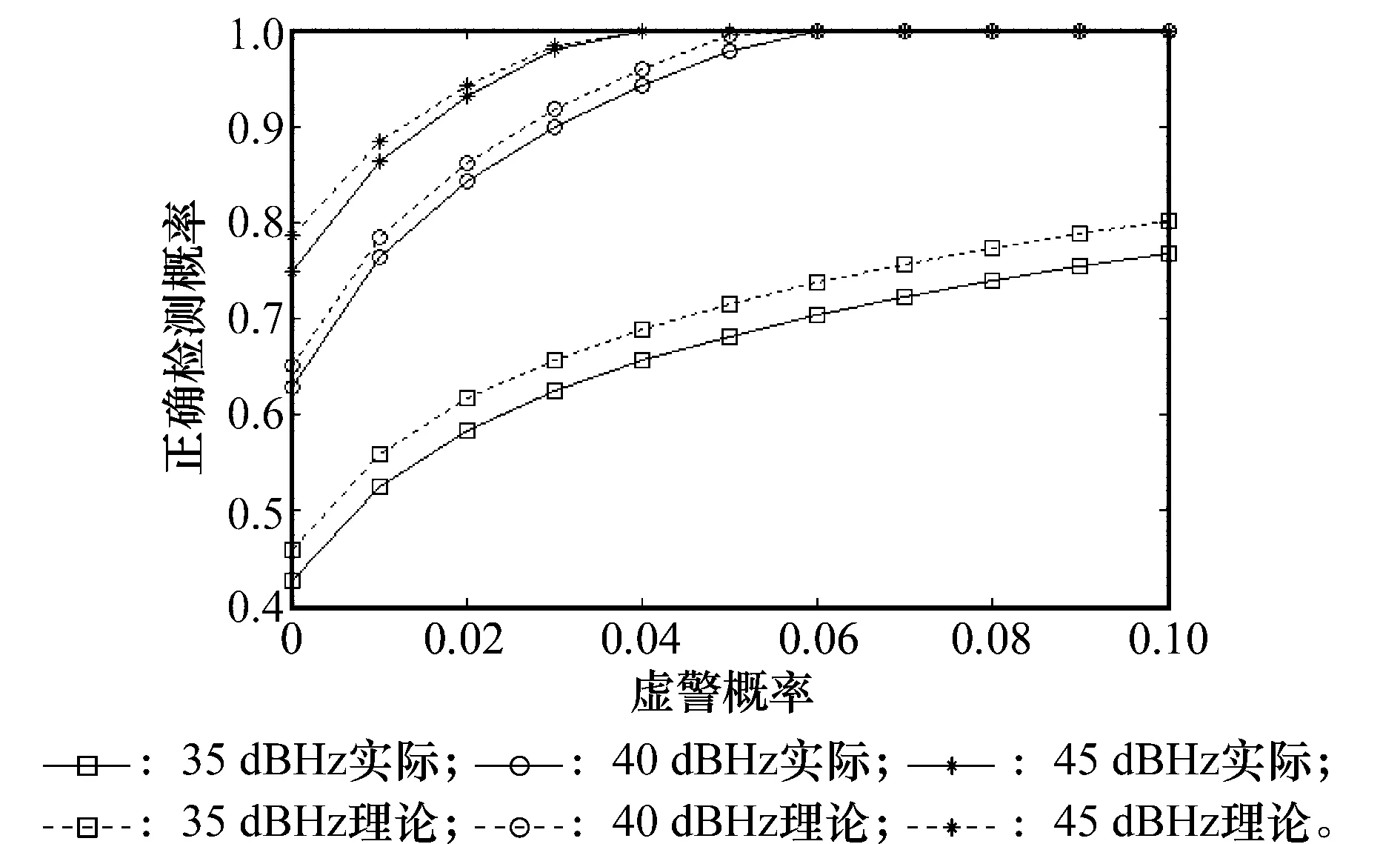
图3 工作特征曲线图Fig.3 Receiver operating characteristic curve
2.2 高动态条件下的比特同步性能分析
为了验证所提方法在高动态条件下的比特同步性能,对相同条件下对传统比特同步方法、参考文献[12]中的方法、本文所提方法进行仿真,并对数据进行100 ms的观测后进行判决。仿真考虑的3种动态情形如表2所示。

表2 仿真参数设置
对于情形1,当载噪比为35 dBHz时,其检测示意图如图4。传统直方图法的检测示意图如图4所示。由于噪声和初始多普勒频偏的干扰,传统方法经过N=5即100 ms的检测与统计,无法根据检测的结果从候选比特跳变位置中判断出比特跳变的实际位置,而所提方法如图5所示。经过5个导航数据比特的检测,其检测峰值处于第11个候选位置。其余候选位置随着远离第11个候选位置其检测结果也逐渐递减,其检测结果具有一定的规律性。
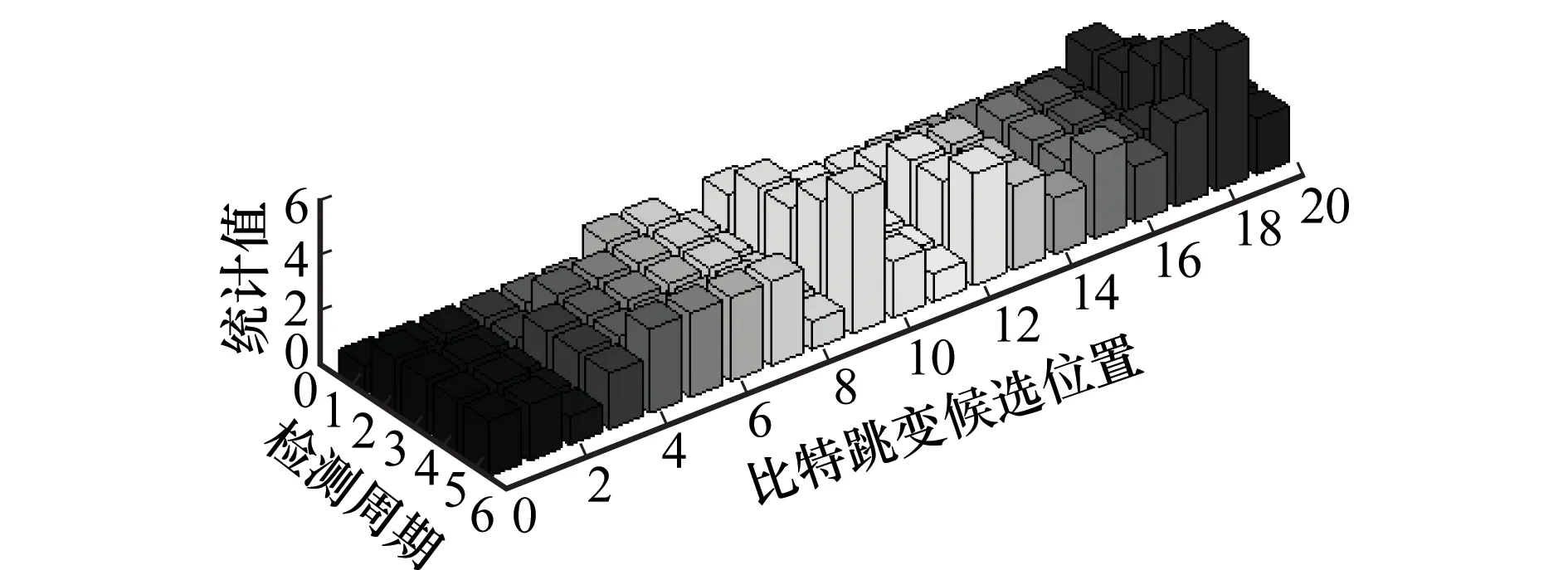
图4 传统方法检测结果Fig.4 Detection result of traditional method
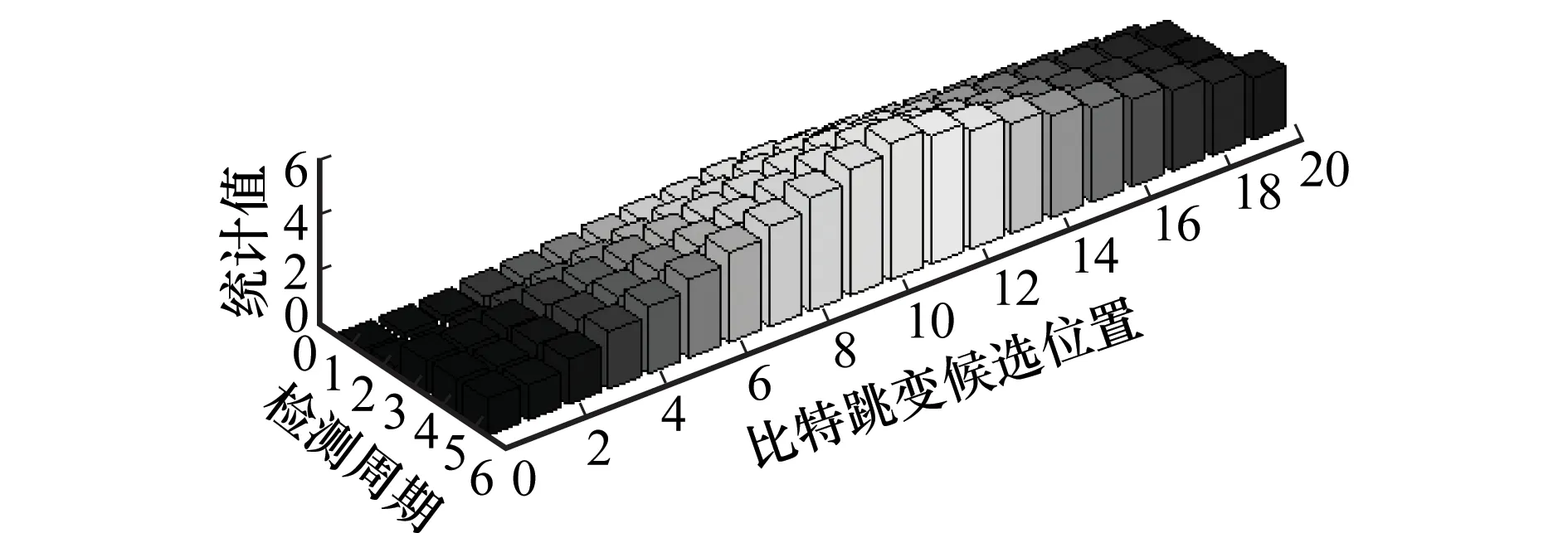
图5 所提方法检测结果Fig.5 Detection result of proposed method
由图6~图8的仿真结果可以看出,在高动态环境下,初始多普勒频和多普勒频偏速率均会严重影响传统比特同步的性能,在3种情景下,传统方法均处于失效状态,其比特同步的正确检测概率也不随信噪比明显变化,且低于0.2,此时传统检测方法基本失效。由仿真的结果同时可以看出,参考文献[12]中的方法(对照方法)具有在高动态条件下比特同步的能力,当多普勒频偏速率增大时,其性能会受到一定的影响。所提的导频辅助下的比特同步方法不仅能够在3种动态情形下正常工作,且在3种情景下变化趋势和性能也基本相同:当载噪比增大,正确检测概率趋近于100%,载噪比由48 dBHz降低到24 dBHz的条件下,所提算法的正确检测概率大约下降0.40~0.43。说明载体的速度和加速度引起的初始多普勒频和多普勒频偏速率的改变对所提方法的影响较低,影响所提方法的主要因素为载噪比的大小,所提方法在高动态条件具有较为可靠的比特同步性能。
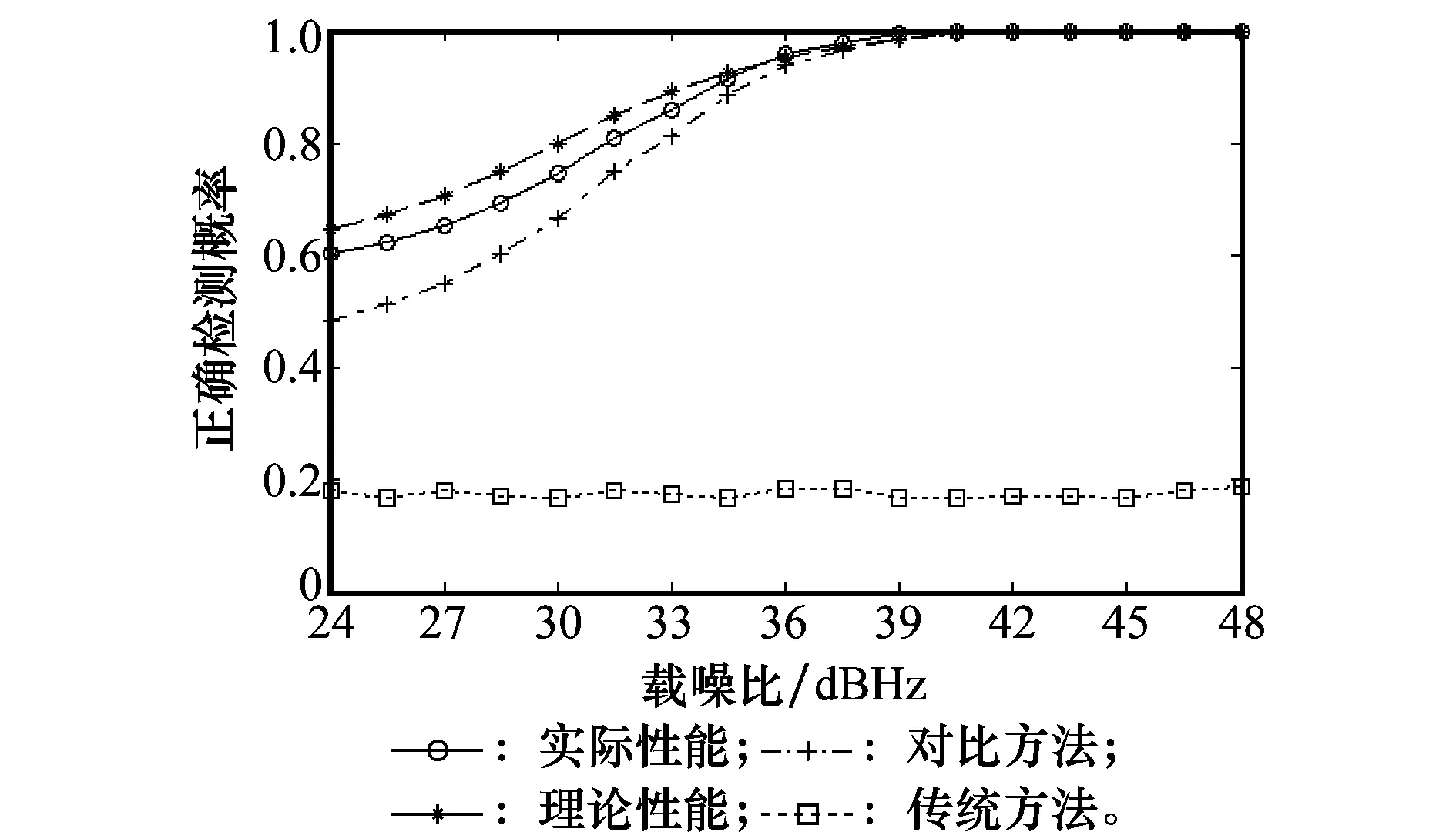
图6 情景1方法性能Fig.6 Method performance in scene 1
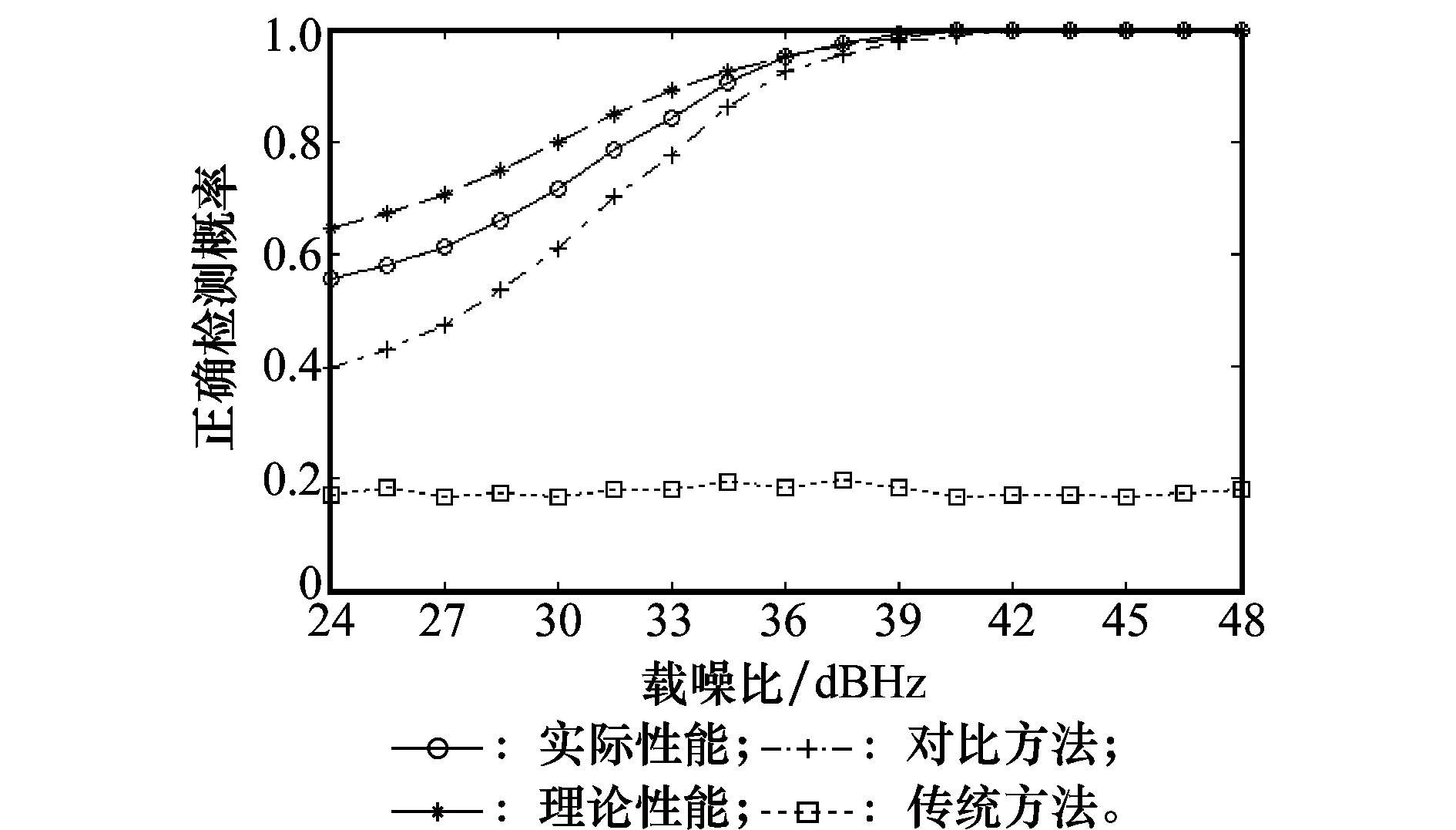
图7 情景2方法性能Fig.7 Method performance in scene 2
图8 情景3方法性能Fig.8 Method performance in scene 3
2.3 检测时间分析
文中第2.1节和第2.2节对信号进行100 ms观测后进行判决。实际情况中不知道载噪比的大小,需要按照式(10)进行若干数据比特的非相干累加后,按照判决门限进行判决。改变判决门限ρthres的大小,同时改变载噪比,统计此时所提算法需要的判决时间,结果如图9所示:判决时间与载噪比和所设判决门限有关,当载噪比较低时而判决门限设置较高时,检测时间会骤增到800 ms以上。实际中应根据载噪比的大小合理设置判决门限,以免造成漏检或虚警。
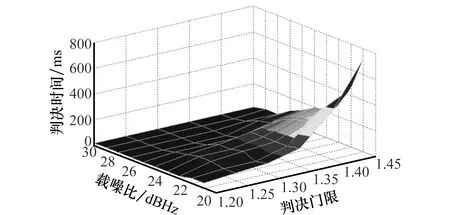
图9 检测时间仿真结果Fig.9 Detection time simulation result
3 结 论
提出一种导频辅助的比特同步方法。由理论推导和仿真实验可以证明,该方法能够非常有效的降低高动态条件下的初始多普勒频偏和多普勒频偏速率对接收机造成的影响,其在高动态条件下的比特同步的性能是传统比特同步方法无法达到的。相比于传统方法,其运算复杂度会有一定程度的增加,但该方法具有工程利用的价值,且易于实现。该方法可以推广到数据信号和导频信号功率按照1∶1正交调制的GNSS频点(北斗B1C频点),也可以应用到数据信号和导频信号同相调制的GNSS频点。
[1] 赵琳,高帅和,丁继成.基于FFT的高动态GPS信号捕获方法优化[J].系统工程与电子技术,2011,33(1):151-156.
ZHAO L, GAO X H, DING J C.Improved acquisition for high dynamic GPS signals based on FFT[J]. Systems Engineering and Electronics, 2011, 33(1):151-156.
[2] 马永奎, 张一, 张中兆,等. 改进的高动态高灵敏度GPS信号捕获算法[J]. 系统工程与电子技术, 2009, 31(2):265-269.
MA Y K, ZHANG Y, ZHANG Z Z, et al. Modified method of high dynamic and high sensitivity GPS signal acquisition[J]. Systems Engineering and Electronics, 2009, 31(2):265-269.
[3] MIAO Z Y, LÜ Y L, XU D J, et al. Analysis of a variational Bayesian adaptive cubature Kalman filter tracking loop for high dynamic conditions[J]. GPS Solutions, 2016, 21(1):1-12.
[4] BETZ J W. Engineering satellite-based navigation and timing: Global navigation satellite systems, signals, and receivers[M].New Jersey: Wiley, 2016:157-405.
[5] LEI D, LU W, ZHANG Y, et al. Balance differential coherent bit synchronization algorithm for GNSS receiver[J]. IEICE Trans.on Communications, 2015, E98.B(6):1133-1140.
[6] SOKOLOVIC V S, MARKOVIC G B, DIKIC G D. Improvement of signal synchronization in GPS software receiver[J]. Military Technical Courier, 2015, 63(4):11-24.
[7] QI J, SONG P. Research on the bit synchronization algorithm and multiplexing technology in GNSS receiver[J].China Communications(English version), 2014,11(s2):30-36.
[8] QUAN Y, LAU L, ROBERTS G W, et al. Measurement signal quality assessment on all available and new signals of multi-GNSS (GPS, GLONASS, Galileo, BDS, and QZSS) with real data[J]. Journal of Navigation, 2015, 69(2):313-334.
[9] 田丰,唐小妹,欧钢.数据和导频通道的功率加权联合捕获算法[J].国防科技大学学报,2016,38(2):112-116.
TIAN F,TANG X M,OU G. Power-weighted combining acquisition algorithm with data and pilot signals[J].Journal of National University of Defense Technology,2016,38(2):112-116.
[10] WARD P W, FUCHSER T D. Stability criteria for GNSS receiver tracking loops[J]. Navigation, 2015, 61(4):293-309.
[11] ELMOWAFY A. Pilot evaluation of integrating GLONASS, Galileo and BeiDou with GPS in Araim[J]. Artificial Satellites, 2016, 51(1):31-44.
[12] 李新山.基于差分相干的微弱GPS信号捕获与比特同步研[D]. 成都:电子科技大学, 2014.
LI X S. Research on weak GPS signal acqucistion and bit synchronization based on differential coherent[D]. Chengdu: University of Electronic Science and Technology of China,2014.
[13] HUANG X M, ZHU X W, TANG X M, et al. Asymmetric AltBOC modulation and its generalised form for BeiDou B2 signals[J]. Electronics Letters, 2016, 52(2):146-148.
[14] ZHU Y, CUI X, LU M. Dual binary phase-shift keying tracking method for Galileo E5 AltBOC(15,10) signal and its thermal noise performance[J]. IET Radar, Sonar & Navigation, 2015, 9(6):669-680.
[15] YANG C, NGUYEN T, BLASCH E, et al. Post-correlation semi-coherent integration for high-dynamic and weak GPS signal acquisition[C]∥Proc.of the IEEE/ION position, location and navigation symposium, 2008:1341-1349.
[16] PAGOT J B, THEVENON P, JULIEN O. Signal quality monitoring for new GNSS signals[C]∥Proc.of the 29th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2016), 2016:1750-1763.
[17] SIMON M K. Probability distributions involving Gaussian random variables[M]. US: Springer, 2006:1-16.
