基于物理光学法的船舶某装置RCS分析∗

张彤 王立 熊勇

（中国舰船研究设计中心 武汉 430064）

1 引言

随着信息化技术的突飞猛进，军事科技得到了日新月异的发展，各个国家的军事探测与攻击能力日益提高。为了增强战争中武器系统的防御能力，越来越多的国家将目光投向隐身技术的研究。雷达是迄今为止最为重要的远程电子探测设备之一，各系统设备只有具有良好的雷达隐身性能，从而在战争中有效规避雷达探测，才能够可靠执行作战任务。

雷达散射截面（RCS）是一个定量描述目标物体对雷达波散射能力的物理量，是衡量其被雷达探测程度的重要因素。现如今，采用新结构新材料降低目标的雷达散射截面（RCS）已成为雷达波隐身技术发展的重要分支。本文针对船舶某装置的RCS展开了仿真分析，探究了在不同频率下装置的几个形状参数对于整体RCS的影响规律，旨在得到最佳的参数设置方案，提高该装置的雷达隐身性能。

2 FEKO软件进行RCS计算的主要算法

FEKO是一种被广泛应用于电磁仿真计算的软件，该软件以矩量法（MOM）为基础，内部集成了多层快速多极子法（MLFMA）、有限元法（FEM）、物理光学法（PO）等多种算法［3］。

矩量法（MOM）是采用FEKO软件进行RCS计算时精确度最高的算法，该算法基于积分方程法［1］，在硬件条件满足的前提下，可对任意复杂目标进行RCS分析。但当采用矩量法分析电大尺寸物体时，剖分合适的网格后将占用巨大的内存［2］。多层快速多极子法（MLFMA）是一种基于分层的数组算法，相较于矩量法，能够更快地解决复杂高频问题，在满足一定精度的条件下提高了运行速度。有限元法（FEM）在非均匀结构的电磁计算中比矩量法占用更小的内存空间。物理光学法（PO）是一种基于麦克斯韦方程组的近似算法，需在目标物体每个面上被激活，该方法广泛应用于电大尺寸物体的电磁计算当中，尤其对于表面光滑的目标具有与精确算法吻合良好的准确度。

3 船舶某装置的RCS仿真分析

3.1 建模情况

为探究该装置的RCS情况，首先在FEKO软件中建立了装置模型：该装置原型为筒形结构，长约1.4m，由三部分构成：上方圆柱、中部圆台、下方圆柱；上方圆柱半径约为0.14m，下方圆柱半径约为0.12m。

图1 装置外形图

本装置的研究频段为8～12GHz，以8GHz为例，可得该频点下的波长为

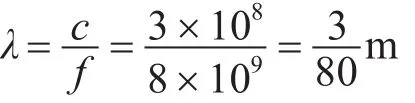
再由装置的最大尺度：

h=1.4m≈37.33λ

因此该装置属于电大尺寸物体。由于FEKO中采用矩量法和快速多极子法仿真时，为了达到较好的准确度都要求剖分网格的尺寸小于λ8，而对于该装置的尺寸情况，必将导致占用巨大的硬件内存和仿真时间。为了提高仿真效率，在综合各种因素后决定将采用物理光学法进行本文的仿真分析。

由于该装置是安装于某船舶的固定位置，故装置尺寸必将受安装空间及周围其他相关设备的限制。经勘测，该装置安装位置的纵向尺寸须固定为1.4m，横向尺寸 ≤0.3m。因此，本文主要探究该装置的径向形状因素对装置整体RCS的影响情况。

为便于研究过程中改变形状参数，这里将装置原型中上方圆柱的上半径设为R、下半径设为R1；下方圆柱的上半径设为R2、下半径设为R3。参数位置如图2所示。

3.2 上方圆台母线倾角α对RCS的影响

改变上方圆柱的上半径R，也即改变其母线倾角α，从而将上方圆柱变为锥度不同的圆台，研究该倾角对装置的周向RCS均值的影响。由于规定该装置的横向尺寸≤0.3m，故要求，也即α需满足：

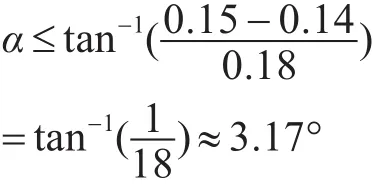
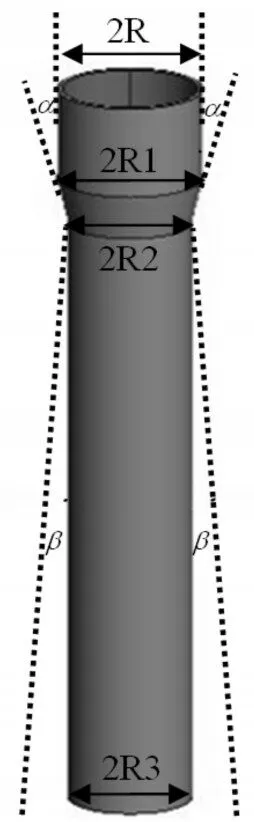
图2 装置形状参数示意图

为留有余量，此处研究的角度范围设定为 -3°＜α＜3°。这里规定 R＞R1时，倾角 α为正；R＜R1时，倾角 α为负，如下图所示分别为 α=3°及α=-3°时的装置建模情况。

图3 上方圆台母线倾角α=3°及α=-3°

在8GHz的频点下，多次改变α的数值，分别仿真计算得到每个α值作对应的周向RCS均值，将结果汇总于下图。

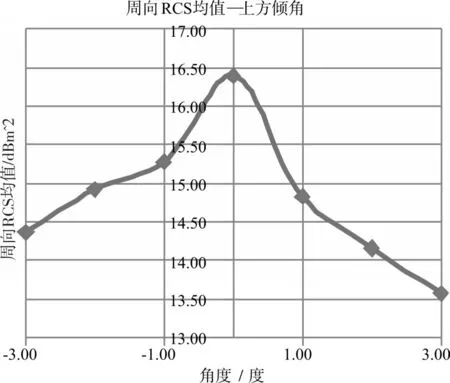
图4 周向RCS均值与上方圆台母线倾角α的关系图线（8GHz）

通过上图结果可知，在8GHz的频点下，当改变α数值时，装置的周向RCS均值随之发生变化，α与周向RCS均值呈现抛物线型相关。当α=0°时，也即装置上面部分为圆柱时，装置的周向RCS均值取得最大值；而当α以0°为中心，向正、负方向变化时，周向RCS均值随之降低。

为了探究在其他频率下周向RCS均值与上方倾角的关系，继续进行9GHz、10GHz、11GHz、12GHz频率下的仿真分析，将所有结果汇总于下图。

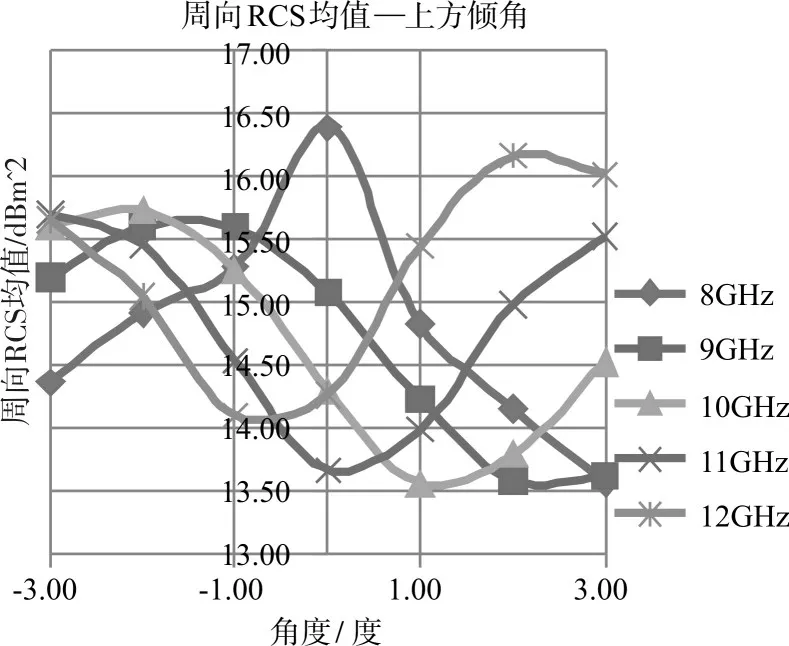
图5 周向RCS均值与上方圆台母线倾角α的关系（8～12GHz）

通过以上汇总结果可知，在不同频率下，装置的周向RCS均值均与上方圆台母线倾角α呈现类抛物线型相关，该相关关系与频率有关，但各频率下的曲线趋势相似。

由于本装置的使用频段为8～12GHz，为了选择一个在整个频段综合性能最好的参数值，将每个α角度对应的五个频点下的周向RCS均值结果再取平均，得到周向RCS均值的频段内均值与上方圆台母线倾角α的关系图线。

图6 周向RCS均值的频段内均值与上方圆台母线倾角α的关系

由以上结果可知，当只考虑装置上方圆台母线倾角α的改变对装置周向RCS均值的影响时，α=1°时对应的周向RCS均值频段内均值最小，意味着该角度下装置的雷达隐身性能最佳。因此，α=1°即为该参数的最佳设置点。

3.3 下方圆台母线倾角β对RCS的影响

改变下方圆柱的下半径R3，也即改变其母线倾角β，从而将下方圆柱变为锥度不同的圆台，研究该倾角对装置的周向RCS均值的影响。由于规定该装置的径向尺寸≤0.3m，故要求=0.15m，也即β需满足：

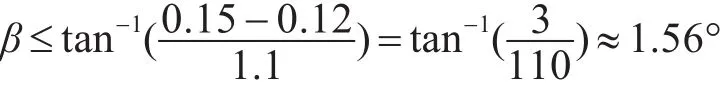
为留有余量，此处研究的角度范围设定为-1.5°＜β＜1.5°。这里规定 R3＞R2时，倾角 β为正；R3＜R2时，倾角 β为负，如下图所示分别为β=1°及 β=-1°时的装置建模情况。

图7 下方圆台母线倾角 β=1°及 β=-1°

在8GHz的频点下，多次改变 β的数值，分别仿真计算得到每个β值作对应的周向RCS均值，将结果汇总于下表。

图8 周向RCS均值与下方圆台母线倾角β的关系图线

通过以上结果图线可知，在8GHz的频点下，当改变β数值时，装置的周向RCS均值随之发生变化，β与周向RCS均值呈现曲线型相关。当β=0°时，也即装置下面部分为圆柱时，周向RCS均值取最大值；而当 β以0°为中心，向正、负方向变化时，周向RCS均值呈现有波动的降低趋势；当β=-0.75°时，取得最小值，此时装置周向RCS均值比原型结果压低约21.6dB。

为了探究在其他频率下周向RCS均值与下方倾角的关系，继续进行9GHz、10GHz、11GHz、12GHz频率下的仿真分析，将所有结果汇总于下图。

图9 周向RCS均值与下方圆台母线倾角β的关系图线（8～12GHz）

通过以上汇总结果可知，在不同频率下，装置的周向RCS均值均与下方圆台母线倾角β呈现曲线型相关，该相关关系与频率有关，但各频率下的曲线趋势相似。

由于本装置的使用频段为8～12GHz，为了选择一个在整个频段综合性能最好的参数值，将每个β角度对应的五个频点下的周向RCS均值结果再取平均，得到周向RCS均值的频段内均值与下方圆台母线倾角的关系图线。

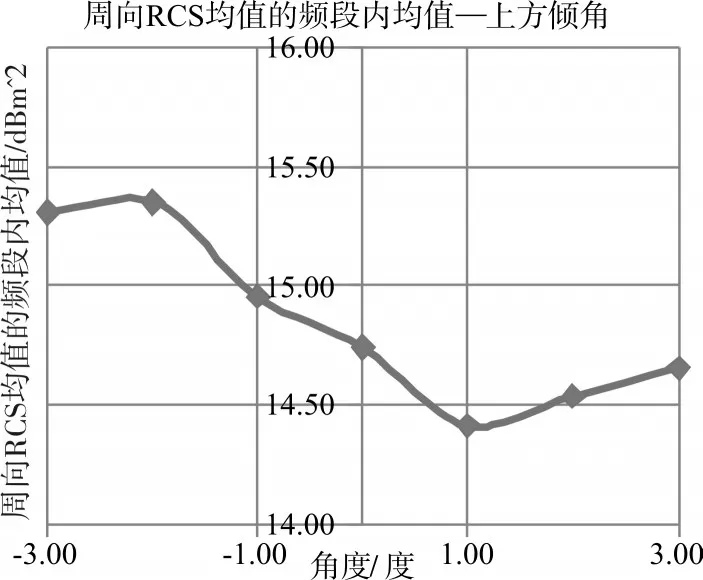
图10 周向RCS均值的各频点均值与下方圆台母线倾角β的关系

由以上结果可知，当只考虑装置下方圆台母线倾角 β的改变对装置周向RCS均值的影响时，β=-0.75°时对应的周向RCS均值频段内均值最小，意味着该角度下装置的雷达隐身性能最佳。因此，β=-0.75°为该参数的最佳设置点。

4 结语

为了提高船舶某装置的雷达波隐身性能，本文主要探究了改变装置的上方圆台母线倾角α和下方圆台母线倾角β对装置整体RCS产生的影响。经仿真分析可知，这两个角度与装置周向RCS均值都呈现曲线型相关，可通过调节两个参数值实现对于装置整体的RCS优化。通过对每个角度对应的多个频点仿真结果进行均值计算，分别得到了装置上方倾角α和下方倾角β的最佳设置点。

本文的分析结果对未来该装置的改装设计具有指导意义，同时也为其他装置的RCS分析提供了可以借鉴的研究方法，有助于实现后期船舶整体雷达波隐身性能的优化。

［1］陈德喜，颜俐，王海婴.FEKO软件的RCS仿真应用［J］.舰船电子工程，2008，28（9）：125-128.

［2］顾俊，王晓冰，梁子长.Feko在复杂目标RCS仿真计算中的应用［C］//安世亚太用户年会论文，2006，11：13.

［3］赵雷鸣，李德银，刘昊.基于FEKO软件仿真计算战斗机的RCS［J］. 计算技术与自动化，2010，29（4）：93-96.

［4］陈武燕.浅谈现代舰船电磁干扰及干扰抑制［J］.船舶，2003（4）：32-34.

［5］朱英富.舰船隐身技术［M］.哈尔滨：哈尔滨工程大学出版社，2015.

［6］孙健，孙剑平，陶熹.舰载电子设备电磁干扰及干扰抑制研究［J］.舰船电子工程，2008（9）.

［7］邱东明，周国军.电磁干扰对舰艇的危害与抑制［J］.辽宁石油化工大学学报，1999（S1）：86-88.

［8］蔡仁钢.电磁兼容原理，设计和预测技术［M］.北京：北京航空航天大学出版社，1997.

［9］张京国，梁晓庚.基于物理光学法和面元法的目标近场 RCS 计算［J］. 探测与控制学报，2008，30（6）：42-45.

［10］陈博韬，雷振亚，谢拥军，等.基于改进物理光学法的电大目标双站RCS的预估［J］.电波科学学报，2010（5）：960-965.

［11］Cown B J，Ryan C E.Near-field scattering measure⁃ments for determining complex target RCS［J］.IEEE Transactions on antennas and propagation，1989，37（5）：576-585.

［12］ Knott E F.Radar cross section measurements［M］.Springer Science&Business Media，2012.