基于阴影法的超声驻波成像和声速测量
2018-02-05张博一李朝荣
胡 斌 夏 珣 熊 畅 张博一 唐 芳 李朝荣
(北京航空航天大学 1电子信息工程学院,2高等理工学院,3物理科学与核能工程学院,4自动化科学与电气工程学院,北京 100191)
超声波是一种纵向机械应力波,当超声波在透明介质中传播时,将引起介质在时间和空间上的周期性弹性应变,导致介质的折射率出现相应的变化。当光波通过这一超声光栅时就会发生衍射现象,其衍射光的强度、频率和方向等都随着超声场的变化而变化,这种现象称为声光效应[1-4]。利用激光通过声光晶体产生的衍射现象测量晶体内部的折射率分布周期,进而得到超声波在晶体中的传播速度,是大学基础物理实验之一,有助于了解声光效应与声光调制的工作原理。
超声场在介质中引起的折射率周期性变化,可以等效为一个光学的“相位光栅”,光栅的周期等于超声波的波长,当光波通过此介质时,就会产生光的衍射。若在晶体后适当位置增加一个凸透镜或凹面镜进行聚焦,在焦点后方用一个长焦距的凸透镜将光线聚焦到测微目镜,则可通过测微目镜观察到晶体内部的超声波波场。由于本实验使用的超声晶体内产生的是超声驻波,所以可观察到超声驻波场像。此方法所利用的阴影法在显示声场、观察流场等领域有较多的应用[5,6]。本文对以上两种方法进行了对比,两种方法获得的测量结果具有基本相同的精确度,衍射方法计算较为简单,而利用阴影法观察现象比较直观,并且仪器更为简单。
1 声光衍射原理
在带有反射面的声光介质中,超声波经过反射叠加后,形成驻波,位移a可以表示为[7-9]
a=2AsinΩt·cosKx
(1)
式中,A为振幅;Ω为角频率;K表示波数;x为波传播方向上的距离。由此得出,在x=nπ/2上的点位移a恒等于零,每隔T/2振动完全消失(T为入射超声波的周期)。
在超声驻波的作用下,声光介质的折射率n(x,t)由下式表示,即
n(x,t)=n0+ΔnsinΩt·cosKx
(2)
式中,n0为未加超声波时声光介质的折射率;Δn为声致折射率改变幅值。当一束波长λ=650nm的激光通过时,就会有类似于光栅产生的衍射现象。在垂直入射情况下,各衍射极大的方位角为
(3)
各级衍射光的强度为
(4)
式中,C为一简单常数,与实际光强振幅有关;q为入射光束宽度;Jm表示m阶Bessel函数;Δφ0为不存在超声波时光波在介质前后两点的相位差。
根据以上结果,使激光垂直入射到经过超声波调制的声光介质中,即可产生拉曼-纳斯衍射,观察到多级衍射光。
声光衍射光路如图1所示。
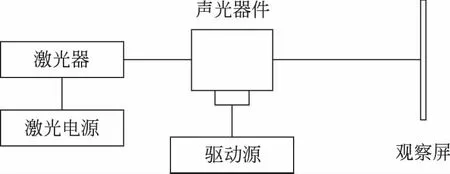
图1 超声驻波场中衍射光路图
2 阴影法观察驻波像原理
将图1中的激光器更换为一束平行光,在声光器件和观察屏之间适当位置处放置两个不同焦距的凸透镜,即构成了阴影法光路。
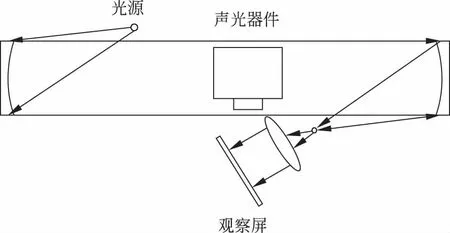
图2 阴影法光路图
因为凸透镜与凹面镜等效,而凹面镜又有色差小等凸透镜不具有的特点,图2所示阴影法光路中采用凹面镜作为产生平行光以及聚焦的光学器件。凸透镜放置在第二个凹面镜焦点后方用于成像,移动观察屏,可找到一个位置使得声光器件在光屏上生成最清晰的像,将光屏换为测微目镜,便可用于观察晶体内部的超声驻波场。晶体内部会出现周期性的明暗相间条纹,相邻明条纹或者暗条纹的间距d对应于半个超声波周长λs/2。这是由于稳定驻波中两个相邻的波节处分别对应介质的疏密分布,而介质的疏密排列对应折射率的大小分布,介质疏密的周期为一个波长。每经过半个超声信号驱动周期,同一波节位置处稠密与稀疏交替变化,即全部稠密变成稀疏或者与此相反,但是由于超声波频率高,变化速度快,视觉暂留效果使得实际观察到的驻波像是两个时刻的驻波像的叠加,因此出现周期为超声波半个波长的明暗相间条纹。测得超声波驻波像中相邻两明纹/暗纹的间距d,即可得到超声波的波长为λs=2d,利用下式即可计算声光介质中的超声波传播速度v,即
v=λsf=k·2d·f
(5)
式中,f为超声波的频率,可从频率计中直接读出;k为缩放比例系数,由于实验中加了透镜成像,故实际观察到的超声驻波像的周期相对于晶体中传播的超声波的波长有一定的放大比例关系,可由声光晶体与透镜的位置关系确定。本实验中通过测量实际晶体宽度D0和晶体像的宽度D得到,即
(6)
3 实验结果
3.1 衍射方法[10]
当激光垂直入射到经声光调制的晶体表面时,将会产生拉曼-纳斯衍射。在远处的光屏上产生如图3所示的关于中央零级对称的多级衍射斑点。

图3 声光拉曼—纳斯衍射产生的衍射斑
由于实际实验中衍射角较小,并且激光不宜用眼睛直接观察,故采用线阵CCD连接示波器代替光屏,通过观察示波器中的波峰位置确定各级衍射之间的距离,实物光路及示波器波形如图4所示。图4(a)为标定总长度的波形,图4(b)为放大2倍后衍射斑间距的波形。
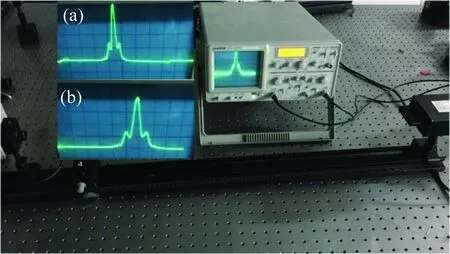
图4 衍射方法测超声波波速实物光路图
在示波器上读出±1级衍射点间的距离,即示波器横轴上的间格数,根据比例关系换算为实际的±1级衍射点与零级衍射点的间距s,在本实验中,s换算方法如下:
(7)
式中,x1为示波器上±1级衍射斑之间的格数,x2为CCD同步信号一个周期所占的格数,并且读取x1时示波器的横向放大倍数是读x2时的两倍;M和w分别表示CCD感光元总数和每个感光元对应的宽度。
再从光具座上读出晶体与CCD之间的距离l,便可得到衍射角
(8)
将θ代入式(3)中(式中,取m=1)算出超声波波长λs,再将λs代入式(5)中,即可算得超声波在晶体中的传播速度。
实验结果如表1所示。

表1 波长的测量
v=λs·f=3804.43(m/s)
(9)

以上各式中用u(x)表示变量x的不确定度,下同。
实验中所用到的声光晶体内超声波速度标准值为3864m/s,计算相对误差为1.7%。
3.2 阴影法
如前所述,将光源更换为点光源,按图2所示阴影法光路搭建实验装置(图5)。在测微目镜中可直接观察到晶体内部的由超声驻波造成的周期性的明暗条纹分布。图6为在测微目镜中观察到的声光晶体中的超声驻波像。

图5 阴影法实验装置图

图6 声光晶体中的驻波像
实际实验中,由于驻波场存在的位置与晶体表面不重合,故当测微目镜位于驻波场最清晰的位置时,晶体边界会产生模糊。在驻波像最清晰的位置处,利用测微目镜测量相邻两明条纹的间距,再将测微目镜移动到边界最清晰处,测量晶体宽度D。实验中使用的凹面镜焦距较大,故略微移动测微目镜造成的缩放比例变化可以忽略不计。
利用测微目镜测量明纹位置的结果如表2所示。
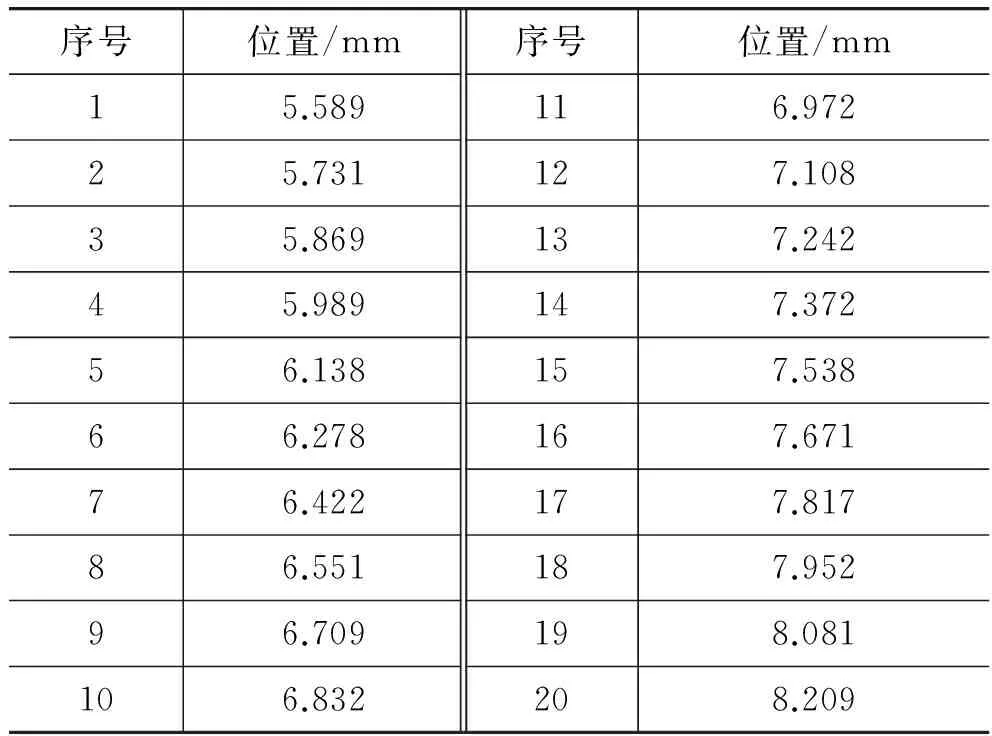
表2 明纹位置的测量
利用逐差法计算得到相邻两明条纹间距的平均值为d=0.13854mm。
使用游标卡尺测量实际晶体的宽度D0见表3。目镜中晶体宽度D=3.806mm。超声波频率f=10.3314MHz。
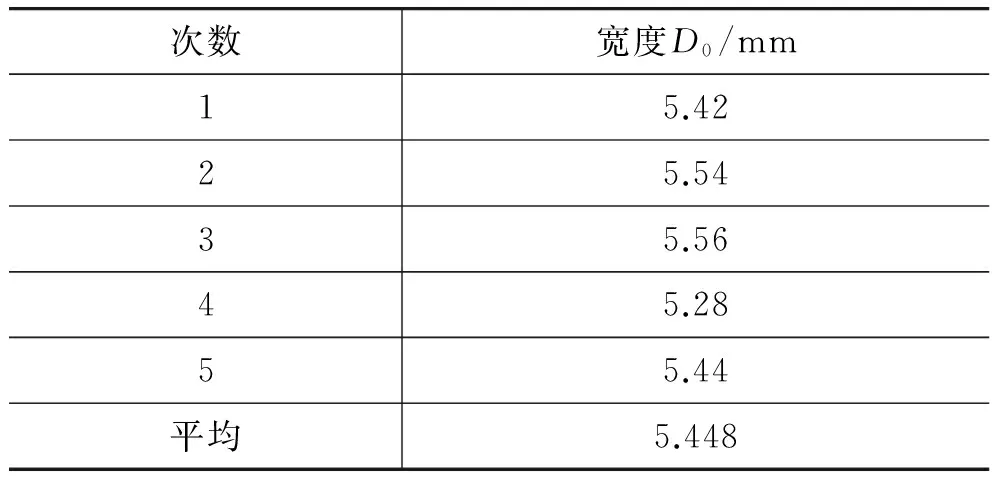
表3 晶体宽度测量
将以上结果代入式(5)中,得到
(17)
计算不确定度:
于是得
u(v)=41m/s
(24)
最终有
v=(4.10±0.04)×103m/s
(25)
与标准理论值比较得到相对误差为6.0%。
3.3 实验对比
从以上两种实验结果可以看出,衍射方法相对误差更小,但在实验设备方面要求更高;而利用阴影法得到的结果不确定度更小,并且可以直接观察晶体内部超声驻波像,使实验者对声光效应以及超声驻波有更直接形象的认识,并且光路可以由简单的凸透镜或凹面镜组合搭建,不需要CCD等贵重仪器。
4 结语
本文从物理实验中观察到的利用阴影法可以看到晶体内部的驻波像这一现象出发,对比了利用光栅衍射规律测量声光介质中超声波传播速度的方法和直接测量介质内部折射率分布周期进而计算超声波波速的方法,分析了两种方法各自的优缺点。使用衍射方法可以较精确地测得声光介质内的超声波传播速度,而使用阴影法有利于深入理解超声驻波在晶体内部的传播现象,并对实验器材的要求更低。
[1] 曹跃祖.声光效应原理及应用[J].物理与工程,2000,10(5):46-47,52.CAOYaozu.Principleandapplicationsofacoustoopticeffect[J].PhysicsandEngineering, 2000,10(5): 45-47,52. (inChinese)
[2] 李明,李冠成.声光效应实验研究[J]. 应用光学,2005,26(6):23-27.LIMing,LIGuancheng.Experimentalinvestigationofacousto-opticeffect[J].JournalofAppliedOptics, 2005, 26(6): 23-27. (inChinese)
[3] 阮立锋,唐志列,刘雪凌. 基于傅里叶分析的拉曼-奈斯声光衍射光强分布的研究[J]. 光学学报, 2013, 33(3):90-95.RUANLifeng,TANGZhilie,LIUXueling.InvestigationonlightintensitydistributionofRaman-Nathacousto-opticdiffractionbasedonFourieranalysis[J].ActaOpticaSinica, 2013, 33(3): 90-95. (inChinese)
[4] 徐介平. 声光器件的原理、设计和应用[M]. 北京:科学出版社, 1982.
[5] 诸国桢,杨旭辉,傅德永. 用阴影法观察水声模型的声场[J].应用声学,2001,20(1):11-14.ZHUGuozhen,YANGXuhui,FUDeyong.Visualizationoftheacousticfieldofseabedmodelbyashadowgraph[J].AppliedAcoustics, 2001, 20(1): 11-14. (inChinese)
[6]DAVIDHAZYA.Introductiontoshadowgraphandschlierenimaging[EB/OL]. 2006.http://scholarworks.rit.edu/article/478.
[7] 李朝荣, 徐平, 唐芳, 等. 基础物理实验[M]. 北京:北京航空航天大学出版社, 2010.
[8] 李武军, 王晓颖. 声光Naman-Nath衍射特性的研究[J]. 大学物理, 2009, 28(9):25-27.LIWujun,WANGXiaoying.Studyoftheacoustic-opticNaman-Nathdiffractivecharacteristic[J].CollegePhysics, 2009, 28(9): 25-27. (inChinese)
[9] 刘海霞, 盖磊, 刘光娟,等. 声光衍射及实验研究[J]. 实验室研究与探索, 2009, 28(1):62-65.LIUHaixia,GAILei,LIUGuangjuan,etal.Theprincipleofacousto-opticdiffractionandexperimentalresearch[J].ResearchandExplorationinLaboratory, 2009, 28(1): 62-65. (inChinese)
[10] 于艳春, 李冠成, 王秉坤,等. 声光效应实验装置及实验研究[J]. 光学仪器, 2004, 26(6):52-57.YUYanchun,LIGuancheng,WANGBinkun,etal.Studiesontheexperimentandexperimentinstallationofacoustoopticeffect[J].OpticalInstruments, 2004, 26(6): 52-57. (inChinese)
