统计物理教学中引入Jarzynski等式的必要性
2018-02-05覃莉
覃 莉
(西北农林科技大学理学院应用物理系,陕西 杨凌 712100)
热力学与统计物理是高等院校物理学专业本科学生必修的基础理论课之一,按照1980年编写的教学大纲,出版了很多相应的教材,如汪志诚编著《热力学·统计物理》[1]、梁希侠、班士良编著《统计热力学》[2]、包景东编著《热力学与统计物理学简明教程》[3]等。但正如Reichal所说:“近年来统计物理领域中出现了许多鼓舞人心的发展,……,使这门学科发生了革命性的变化。”这些变化在教材或教学的讨论课程中应该有所体现,比如已经被理论和实验证明了的具有普适性的一个等式——Jarzynski等式。
1 Jarzynski等式
20世纪90年代以来,统计物理学界最重要的成果之一是Jarzynski在1997年得到的一个令人振奋和惊奇的远离平衡态等式,称为Jarzynski等式[4]。根据该等式可以由非平衡物理过程中功的测量来计算两个平衡态之间的Helmholtz自由能的差,这与传统的热力学观念截然相反。考虑一个处于温度为T的热浴中的系统,其状态由控制参量λ决定。初始时使系统处于平衡态A,参量为λA。改变λ,使其随时间变化,则平衡被破坏。经过有限时间τ,变化到λB。一般地,由于过程不一定是可逆过程,在操作的末端,系统仍处于非平衡态,但是如果此时让参量保持λB演化一段时间,则系统最后弛豫到新的平衡态B。这个过程如图1所示[5,6]。
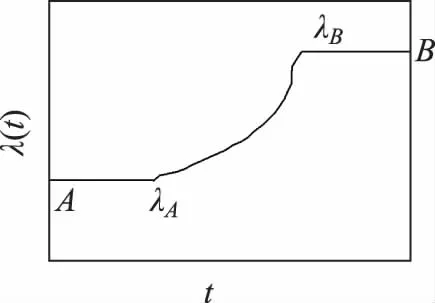
图1 Jarzynski等式所描述的非平衡过程
Jarzynski等式是关于图1过程中的功和自由能的关系为
(1)
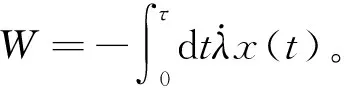
W的大小与两个因素有关:一是系统经历的具体微观态,二是环境对这些微观态的影响。为了确定W的大小,要多次重复这个过程然后求平均,式(1)右边的尖括号即表示对这些过程的系综平均[7]。
2 Jarzynski等式的普适性
自从Jarzynski等式在1997年被发现之后,该等式的广泛适用性就一直是一个很有意义的研究课题。物理学者希望可以找到该等式严格成立的物理条件,越广泛越好。比如钱敏等以非时齐马氏链和多维扩散过程为模型,第一次给出了Jarzynski等式的比较完整的数学理论[8];Hatano和Sasa把Jarzynski等式推广到非平衡定态的情形[9];王向斌等运用量子态耗散方法(QSD)轨迹,第一次推导出非平衡体系在量子非马尔可夫下的Jarzynski等式[10];Deffner和Saxena讨论了宇称时间对称量子力学中的Jarzynski等式问题等[11]。这些年来的研究表明,Jarzynski等式可以在确定性力学体系中得到,在一般的采用随机描述的体系中也可以得到[4,12];在Jarzynski等式中,系统可以是经典的或者量子的[4,10,13];所考虑的随机过程可以是马尔科夫或者非马尔科夫的[14-16];在初末状态是非平衡定态甚至是任意的状态时,Jarzynski等式也可以推广[9,17]。总之,Jarzynski等式具有广泛的适用性。
3 Jarzynski等式的实验验证
单分子实验技术的快速发展,使得在实验中追踪单个的分子成为可能。Hummer和 Szabo注意到Jarzynski等式的生物物理关联,指出如何从非平衡条件下的单分子实验中得到自由能[18]。随后,Liphardt和Bustanmante等人通过著名的生物单分子实验证明了Jarzynski等式,其实验新颖之处在于成功地使用光镊控制单个生物小分子,进行关于细胞单分子的力、位移和能量的测量。他们发现,利用平均功、涨落耗散定理、Jarzynski等式这3种方法估算自由能,Jarzynski等式给出的结果与十分缓慢的拉伸过程中算出的可逆功最为接近,且误差在热运动能量范围内[19,20]。2006年,Blickle等人用非简谐势场中的胶体微粒验证了Jarzynski等式[21];2007年,Sylvain等人用简谐振子证明了Jarzynski等式[22]。2015年清华大学交叉信息研究院量子信息中心金奇奂带领的离子阱实验小组,在试验中验证了量子Jarzynski等式[23]。
4 结语
用Jarzynski等式可以计算两平衡态间Helmholz自由能的变化,由有限时间的非平衡过程的功给出。而在传统的热力学里,为了计算两个平衡态之间的自由能差,我们必须在这两平衡态之间构造一个无穷慢的准静态过程,通过测量这个过程中系统所做的功来计算。
Jarzynski等式还可以写成另一种形式:
〈e-Wdiss/kBT〉=1
其中Wdiss=W-ΔF为进入到外界环境之中的耗散功。该式暗含了〈Wdiss〉≥0。对于宏观系统,这即为热力学第二定律的自由能和功的表述。由该等式还可以得到一个重要的推论:虽然〈Wdiss〉≥0,但是只有在有部分轨道Wdiss<0的情况下等号才能成立。这些轨道违反了热力学第二定律,以保证微观运动方程是时间可逆的。也就是说,对于宏观系统,Jarzynski等式和热力学第二定律是一致的;对于微观系统,物理量的统计平均仍然满足热力学第二定律,但是Jarzynski等式包含了更为丰富的信息。应用Jarzynski等式,可以从系统对非平衡过程的响应得到平衡态的信息,还可以把与热力学第二定律有关的不等式写成等式。Jarzynski等式揭示了热力学第二定律在微观尺度是如何起作用的,从而能够加深对热力学第二定律的理解[7]。Jarzynski等式的证明,基本上使用初等数学的方法就可以了。这从另一个侧面,表明Jarzynski等式是物理世界中一个非常本质的规律。正因为如此,我们认为,Jarzynski等式应该引入到统计物理的教材或教学的讨论课程中。
[1] 汪志诚. 热力学·统计物理[M]. 北京: 高等教育出版社, 1996.
[2] 梁希侠, 班士良. 统计热力学[M]. 北京: 科学出版社, 2008.
[3] 包景东. 热力学与统计物理简明教程[M]. 北京: 高等教育出版社, 2011.
[4] JARZYNSKI C. Nonequilibrium equality for free energy differences [J]. Phys. Rev. Lett., 1997, 78(14): 2690-2693.
[5] 覃莉. 小系统涨落定理及各态历经行为的研究[D]. 北京: 北京师范大学, 2009. QIN Li. Studies on fluctuation theorems and nonergodic behavior of small systems [D]. Beijing: Beijing Normal University, 2009. (in Chinese)
[6] BUSTAMANTE C, LIPHARDT J, RITORT F. The nonequilibrium thermodynamics of small systems [J]. Phys. Today, 2005, 58(7): 43-48.
[7] 怀小鹏. 涨落定理和不可逆性[D]. 杭州: 浙江大学, 2012. HUAI Xiaopeng. Fluctuation theorems and irreversibility [D]. Hangzhou: Zhejiang University, 2012. (in Chinese)
[8] 葛颢. 随机过程在非平衡态统计物理和系统生物学建模中的应用[D]. 北京: 北京大学, 2008. GE Hao. Applications of stochastic processes into nonequilibrium statistical physics and systems biology[D]. Beijing: Peking University, 2008. (in Chinese)
[9] HATANO T, SASA S. Steady-states thermodynamics of Langevin systems [J]. Phys. Rev. Lett., 2001, 86(16): 3463-3466.
[10] 陈天. 量子体系的能量操控以及微观器件的研究[D]. 北京: 清华大学, 2015. CHEN Tian. Manipulation of thermal flux in quantum systems and study of microscopic Devices[D]. Beijing: Tsinghua University, 2015. (in Chinese)
[11] DEFFNER S, SAXENA A. Jarzynski equality in PT-symmetric quantum mechanics [J]. Phys. Rev. Lett., 2015, 114(15): 150601.
[12] CHERNYAK V Y, CHERTKOV M, JARZYNSKI C. Path-integral analysis of fluctuation theorems for general Langevin processes[J]. J. Stat. Mech., 2006, P08001.
[13] ANDRIEUX D, GASPARD P. Quantum work relations and response theory [J]. Phys. Rev. Lett., 2008. 100(23): 230404.
[14] SPECK T, SEIFERT U. The Jarzynski relation, fluctuation theorems, and stochastic thermodynamics for non-Markovian processes [J]. J. Stat. Mech.-Theory E., 2007, L09002.
[15] OHKUMA T, OHTA T. Fluctuation theorems for non-linear generalized Langevin systems [J]. J. Stat. Mech.-Theory E., 2007, P10010.
[16] 江惠军. 介观统计力学规律与方法的研究[D]. 合肥: 中国科学技术大学, 2011. JIANG Huijun. Studies of mechanism and method on mesoscopic statistical mechanics[D]. Hefei: University of Science and Technology of China, 2011. (in Chinese)
[17] GONG Z P, QUAN H T. Jarzynski equality, Crooks fluctuation theorem, and the fluctuation theorems of heat for arbitrary initial states [J]. Phys. Rev. E, 2015, 92(1): 012131.
[18] HUMMER G, SZABO A. Free energy reconstruction from nonequilibrium single-molecule pulling experiments [J]. Proc. Natl. Acad. Sci. USA, 2001,98(7): 3658-3661.
[19] LIPHARDT J, DUMONT S, SMITH S B, et al. Equilibrium information from nonequilibrium measurements in an experimental test of Jarzynski’s equality [J]. Science, 296(5574), 2002: 1832-1835.
[20] 涂展春. 小系统的非平衡统计力学与随机热力学[J]. 物理, 2014, 43(7): 453-459. TU Zhanchun. Nonequilibrium statistical mechanics and stochastic thermodynamics of small systems[J]. Physics, 2014, 43(7): 453-459.(in Chinese)
[21] BLICKLE V, SPECK T, HELDEN L, et al. Thermodynamics of a colloidal particle in a time-dependent nonharmonic potential [J]. Phys. Rev. Lett., 2006, 96(7): 070603.
[22] JOUBAUD S, GARNIER N B, DOUARCHE F, et al. Experimental study of work fluctuations in a harmonic oscillator [J]. C. R. Physigue, 2007, 8(5-6): 518-527.
[23] AN S M, ZHANG J N, UM M, et al. Experimental test of the quantum Jarzynski equality with a trapped-ion system [J]. Nature Phys., 2015, 11(2): 193-199.
