基于遗传算法的AR谱极点频率优化方法及应用

明廷锋， 张 帅

(海军工程大学 动力工程学院， 湖北 武汉 430033)

提取故障特征频率是机械故障诊断过程中的关键步骤， 也是故障诊断领域的研究热点之一. 例如对于滚动轴承的故障诊断， 相关研究已经有二十多年了， 最常用的方法就是对轴承的故障信号进行分析和处理从而得出相关的故障特征， 具体包括时频分析、 能量谱分析等[1-11]， 这些方法已经能够成功地对很多机械进行故障检测. 近年来， Suguna提出了一种基于自回归模型(Autoregressive model, AR)和相关极点谱分解技术的故障检测方法[12]， 它能直接对有用的频率进行分析， 从而避免了对整个频谱进行计算， 很大程度上提高了检测效率和自动化水平. 从信号的AR谱中分解出的几个极点与信号能量谱中的极点是相对应的[13]. 利用AR谱进行故障检测不需要获得整个谱， 只要对几个靠近故障频率的极点进行检测即可. AR谱的极点值只需通过估计出AR系数就能很容易得到. 较小阶数的AR模型就能够很有效地对相关故障频率对应的极点进行估计. AR谱估计需要的信号长度短， 但却可以达到较好的分辨率， 即便是样本的采样频率比奈奎斯特采样频率略高， 也能表现出不错的分辨率. 但是AR模型的准确性受模型阶数和样本大小的影响， 如果阶数和样本大小选择得不适宜会导致AR谱极点对应的频率较大地偏离对应的故障频率， 从而导致在检测过程中对故障种类产生误判， 最终造成对故障严重程度的判断失误. 而且AR谱极点对应的故障频率本身就会有偏差， 所以选择一个较好的阶数和样本大小是使用AR谱的关键.

目前， 针对AR谱的阶数问题已有很多研究[14]， 但大多都是用一般的定阶准则来确定模型阶数的. 虽然一般的定阶准则在一定程度上能够使模型变得相对准确， 但是这些定阶准则算出的阶数并不是最优阶数. 而且这些阶数很不稳定， 有时也会让AR谱中极点与其对应的故障频率产生很大的偏差. 为了能够得到相对更为准确的阶数和相适应的样本大小， 本文提出了一种基于遗传算法[15]的AR谱极点频率优化方法： 首先对故障信号进行预处理(共振解调、 平方包络等)， 得出轴承的故障频率， 然后利用遗传算法和相关故障频率对预处理后的故障信号AR谱极点进行优化， 使AR谱极点与对应的故障频率相接近， 让故障检测更为准确. 本文对轴承内圈故障信号数据进行了实验验证， 取得了较好的效果， 并得出了较优的模型阶数和样本点数， 为AR谱的定阶和样本点数选择提供了可靠的依据.

1 基于AR谱的故障检测技术

AR谱技术是一种现代谱分析技术， 它同时兼顾了较高的分辨率和较小的计算量， 既高效又简单， 其表达式如式(1)所示.

(1)

式中：ak为自回归系数；e[t]为白噪声序列. 式(1)经过z变换之后得到

(2)

(3)

将式(3)中的分母写成零点式得到

(4)

式中：pk可以通过对式(3)的分母求根得到. 再由式(4)可以推导出

(5)

式中：σ2为白噪声的方差； Δt为信号的采样周期. 从式(4)～(5)中可以看出， 式(4)中的每一个极点pk在式(5)中都有一个频率f相对应. 一般情况下， 这些极点pk所对应的f就是我们要关注的故障频率. 与这些f对应的p[z]就可以作为轴承的健康指标， 通过实时检测这些f对应的p[z]就可以知道轴承的状态. 为了方便进行故障检测， 把f和p[z]反映到极坐标图中， 换算公式如下

ρ=p[z],

(6)

(7)

式中： 用极半径ρ长度表示p[z]； 极角θ为故障频率f在极坐标中的分布；fs为信号采样频率；ω用来调整极径分布的密集程度， 以方便进行检测， 具体的取值根据实际需要而定. 检测流程如图 1 所示. 利用极坐标图进行检测前需要先把轴承的各理论故障频率标注在极坐标上， 然后在检测的过程中把AR谱中的极点转换到极坐标中， 在各理论故障频率极径上设定最大故障值λn， 就可以进行实时检测了.

本文的实验数据均来自凯斯西储大学轴承数据中心网站(http:∥csegroups.case.edu/bearingdatacenter). 实验选取的具体轴承型号是6205-2RS JEM SKF， 深沟球轴承： 滚子 9个， 滚子直径7.9 mm， 中径39 mm. 电机转速为1 730 rpm， 理论故障频率经计算可得： 内圈故障156 Hz， 外圈故障103 Hz， 滚子故障67 Hz， 保持架故障11 Hz. 采样频率为12 000 Hz， 故障信号样本点数是5 000， 图中AR谱的定阶方法都采用AIC定阶方法和Yule-Walker估计法. 图 2(a) 是内圈故障轴承振动信号时域图， 图 2(b) 是经过平方包络处理后的振动信号， 图3是平方包络谱的AR谱和FFT频谱， 可见AR谱的最大极点与FFT的故障频率是相对应的. 利用式(6)作出理论故障频率的极径，ω取值设为20， 对应的故障极角为： 内圈故障93.6°， 外圈故障61.8°， 滚子故障40.2°， 保持架故障6.6°. 图 3 中的检测样本点是取自此故障轴承的一段点数为240 000的信号， 将此信号平均截成100组信号， 每组长度为2 400点数. 对每组信号按照流程图 1 进行故障检测， 得到检测图如图 4 所示. 可见， 当利用AR谱进行故障检测时， 如果最大极值点对应的频率介于两故障频率之间会引起故障类型的误判. 由于每种故障的最大故障值λn是不一样的， 因此会导致对最大故

障值的误判， 最终影响故障检测. 为了能够让AR谱中最大极值点对应的频率与故障频率的偏差尽量小， 就必须选择一个较好的阶数和样本点数.

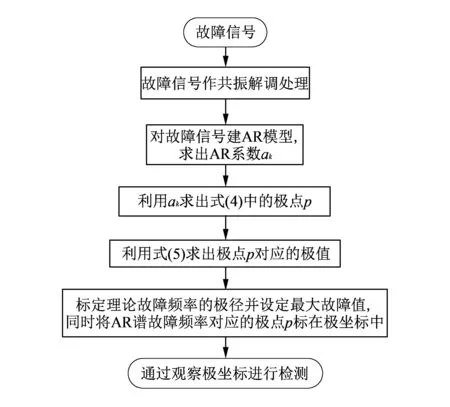
图 1 故障检测流程图Fig.1 Fault detection flowchart

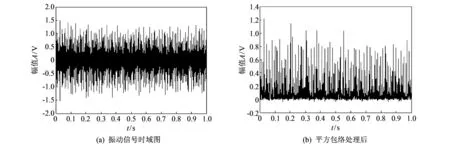
图 2 内圈故障轴承振动信号Fig.2 Vibration signals of bearing inner race fault

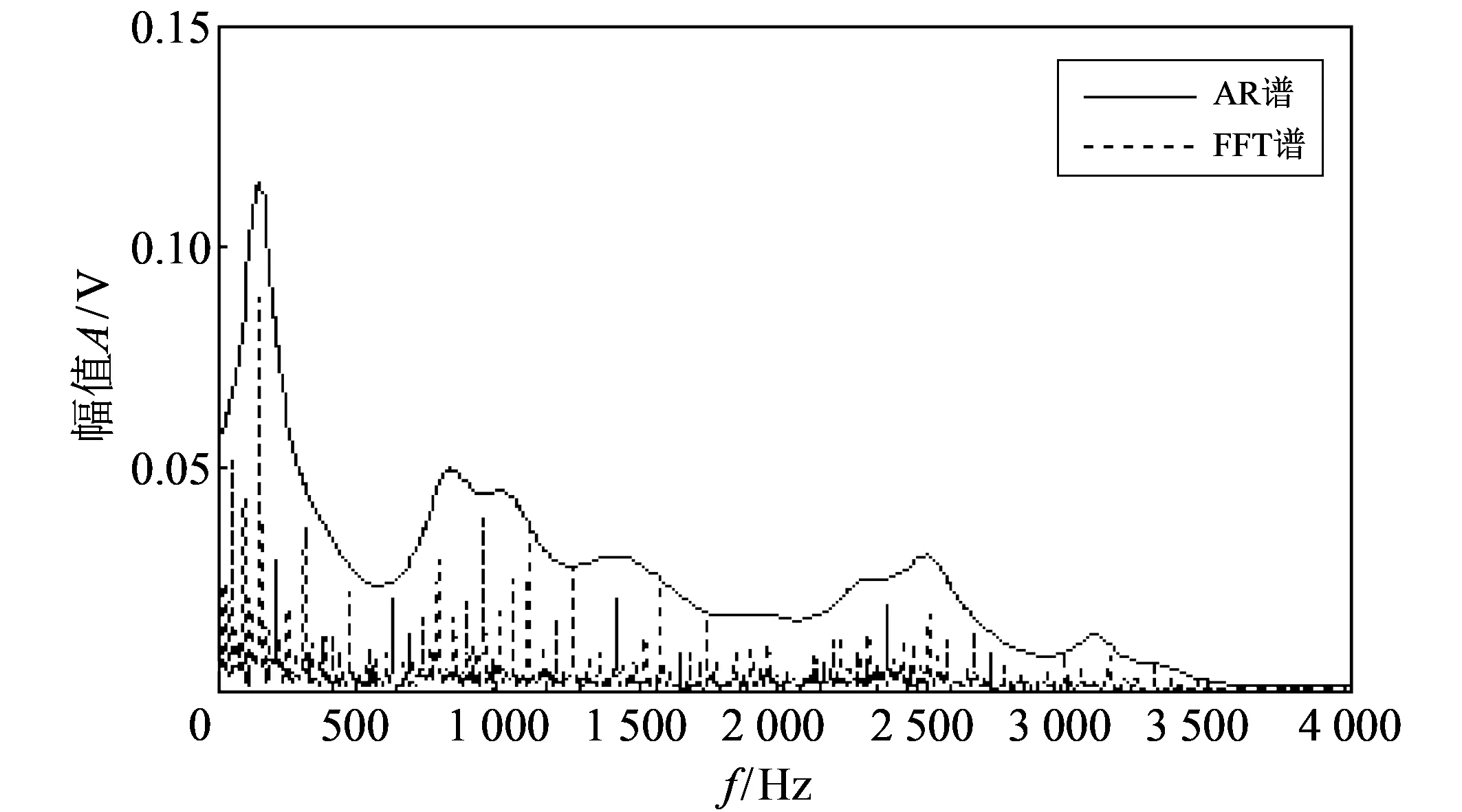
图 3 平方包络信号的AR谱和FFT频谱Fig.3 AR spectrum and FFT spectrum of squared envelope signals

图 4 故障检测极坐标图Fig.4 Fault detection polar coordinates

2 基于遗传算法的AR谱优化算法

目前， 时间序列中常用的定阶方法有很多， 如FPE， AIC， MDL， CAT等. 但这些定阶方法不能很好地满足基于AR谱的故障检测的需要， 有时会产生很大的偏差， 如上节所述. 实际应用时， 可以将这些定阶准则当作一定的参考. 一些研究得出了模型阶数和样本大小的一般取值范围[8]. 本文利用遗传算法对AR谱进行优化， 使AR谱的最大值极点与故障频率更接近， 同时得到了对应的模型阶数和样本点数， 从而更好地实现故障检测.

2.1 遗传算法编码

本算法中的编码采用二进制编码， 共需要2段编码， 每段编码位数是10位. 第一段为AR模型阶数K的偏码， 第二段为样本数为N的编码. 具体如图 5 所示， *代表二进制编码0或1. 编码的换算如式(8)～(9). AR模型的阶数取值一般为25～45， 样本点数的取值范围可以根据需要进行设置， 不同的点数都会对应一个较优的阶数. 一般的定阶准则在4 000时能呈现出较好的效果， 所以本文将其范围定为2 000～6 000以便设置初始种群.

图 5 二进制编码图Fig.5 Binary coded

(8)

(9)

2.2 遗传算法操作步骤

编码完成后就可以进行遗传运算， 具体过程如下：

1) 设置起始种群. 遗传算法起始种群的编码是随机产生的. 它们的取值范围是在阶数和样本大小的一般取值范围内随机选择的， 当然也可以按照对样本大小和阶数的需求设置编码取值范围. 种群的起始数量按照经验进行判断， 从实验中发现40～100较为合适， 文中设为60.

2) 种群的适应性. 为了让AR谱的极点对应的频率与故障频率更接近， 选择故障频率作为比较对像. 把AR谱的极点频率与轴承故障频率的误差作为适应度， 误差越小， 适应性越强. 为了方便适应度的比较， 具体公式如下

S(f)=ft-|f-ft|,

(10)

式中：f为极点频率；ft为轴承的故障频率， 并由共振解调等信号处理方法预先算出， 或根据需要换成理论故障频率；S为适应度，S的值越大， 表示适应性越强.

3) 复制. 复制操作能够决定适应性较强的个体进入下一代， 本文采用的是赌轮盘选择法. 当适应性概率大于复制概率时， 部分子代就可以复制并继承父代的编码. 适应性概率计算如下

(11)

(12)

4) 交叉. 群体中的每个个体之间都以一定的概率pc交叉， 即两个个体从各自字符串的某一位置开始互相交换， 这类似生物进化过程中的基因分裂与重组. 概率pc按照经验进行选取.

图 6 基于遗传算法的优化的流程图Fig.6 Optimization based on genetic algorithm flowchart

5) 变异. 基因的突变普遍存在于生物的进化过程中. 变异是指父代中的每个个体的每一位都以概率pm翻转， 即由“1”变为“0”， 或由“0”变为“1”. 遗传算法的变异特性可以使求解过程随机地搜索到解可能存在的整个空间， 因此可以在一定程度上求得全局最优解.

6) 运算结束. 当出现以下情况时可以结束运算： ① 当个体的适应度发生了收敛， 即在进行了相当次数的迭代后， 适应度的最大值没有明显的变化； ② 当迭代的次数达到了设定的迭代次数. 本算法的流程图如图 6 所示.

3 实验验证

实验验证仍然利用前文所述的实验平台. 信号采样长度为500 000， 均分为100组信号， 每组5 000个. 设置的阶数范围为25～45， 样本点数范围为2 000～6 000. 基于遗传算法优化的故障检测结果图 7 所示.

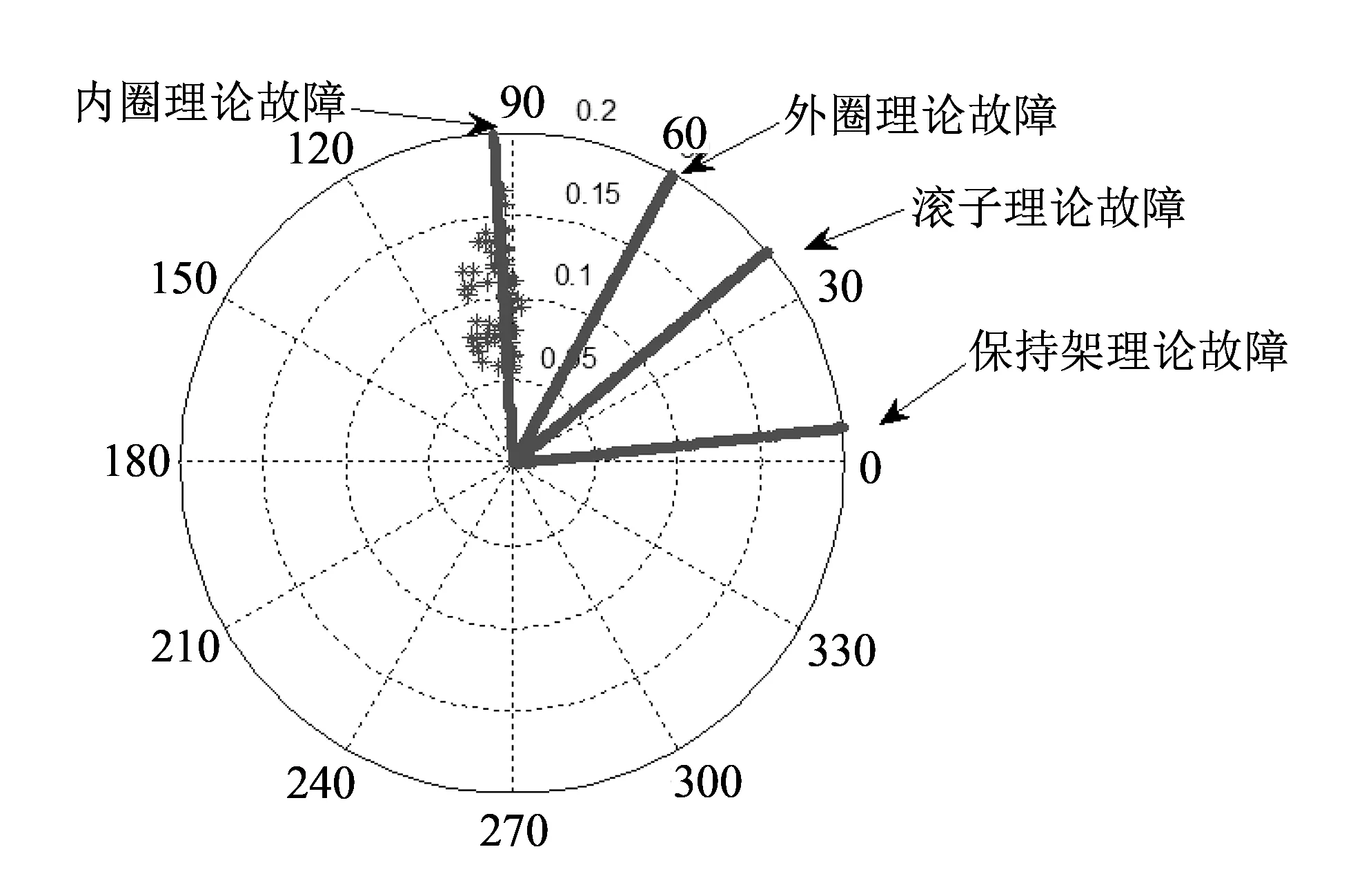
图 7 基于遗传算法的故障检测极坐标图 Fig.7 Fault detection polar coordinates based on genetic algorithm

与图4比较， 易看出优化后的图7的极坐标图很清晰， 故障基本上都集中在内圈故障附近， 与相临的故障极径区域没有重叠的部分， 那么就可以只针对内圈故障进行检测和判断， 而不需要考虑与其相邻的理论故障的检测. 而图4中的检测值则分布在内圈和外圈的理论故障之间的区域， 无法进行精确故障诊断. 图8(a)是经过遗传优化后的AR谱和FFT谱， 图8(b)是用AIC定阶准则直接得出的AR谱. 从图8(a)中可以看出最大的极点对应的频率更接近故障频率， 而图8(b)中有较明显的偏差. 对其它的样本进行优化后， 也得到同样的结果. 因此， 本算法较一般的定阶准则有明显的改进.

图 8 信号的AR谱和FFT谱图Fig.8 AR spectrum and FFT spectrum of the signals

表 1 所示为100个信号样本进行阶数和样本点数优化后的部分数据. 从表1中可以看出， 同一机械系统中同一类型轴承在一定的故障时间段的AR谱阶数基本上是很稳定的， 与之对应的样本点数总体上也是比较稳定的. 因此， 在应用AR谱进行故障检测时， 只需在整个故障检测周期的某几个阶段进行基于遗传算法的AR谱优化， 就可以得出适用于这几个故障检测周期所需的最优模型阶数和点数.

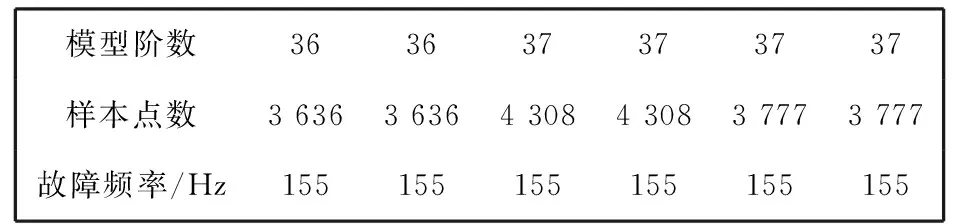
表 1 优化阶数和样本点数

4 结 论

1) 针对基于AR谱中的故障频率与相关极点的偏差问题， 提出了一种基于遗传算法的AR谱故障频率极点优化方法， 使AR谱极点与其对应的故障频率更接近， 从而实现了精确故障检测， 并通过实验数据验证取得了较好的结果.

2) 影响AR模型的因素中除了阶数和样本点数外， 还有估计法的影响， 本文只考虑了采用Yule-Walker估计法， 而最小二乘法、 Burg估计法等也可以应用文中提出的方法进行频谱频率估计， 可在后续研究工作中开展.

[1]McInerny S A， Dai Y. Basic vibration signal processing for bearing fault detection[J]. IEEE Transactions on Education, 2003, 46(1)： 149-156.

[2]Wang W, Wong W K. Some new signal processing approaches for gear fault diagnosis[C]. Proceedings of the Fifth International Symposium on Signal Processing and Its Applications, IEEE, 1999： 587-590.

[3]Tandon N, Choudhury A. A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings[J]. Tribology International, 1999, 32(8)： 469-480.

[4]Stack J R, Habetler T G, Harley R G. Fault classification and fault signature production for rolling element bearings in electric machines[C]. Proceedings of the IEEE International Symposium on Diagnostics for Electric Machines, IEEE, 2003： 172-176.

[5]唐贵基, 庞彬. ITT变换在风电机组滚动轴承故障诊断中的应用[EB/OL]. (2017-09-10)[2017-09-04]. http:∥kns.cnki.net/kcms/detail/32.1318.TM.20170904.1345.023.html.

[6]胡爱军, 马万里, 唐贵基. 基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J]. 中国电机工程学报, 2012, 32(11): 106-112. Hu Aijun, Ma Wanli, Tang Guiji. Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and Kurtosis criterion[J]. Proceedings of the CSEE, 2012, 32(11): 106-112. (in Chinese)

[7]王建国, 李健, 万旭东. 基于奇异值分解和局域均值分解的滚动轴承故障特征提取方法[J]. 机械工程学报, 2015, 51(3)： 104-110. Wang Jianguo, Li Jian, Wan Xudong. Fault feature extraction method of rolling bearings based on singular value decomposition and local mean decomposition[J]. Journal of Mechanical Engineering, 2015, 51(3): 104-110. (in Chinese)

[8]侯新国, 牛超, 杨忠林. 基于最优Morlet小波自适应包络解调的弱故障特征提取方法[J]. 电机与控制学报, 2016, 20(10)： 88-93. Hou Xinguo, Niu Chao, Yang Zhonglin. Method to extract weak fault feature based on optimal Morlet wavelet adaptive envelope demodulation[J]. Electric Machines and Control, 2016, 20(10): 88-93. (in Chinese)

[9]张菀, 贾民平, 朱林. 一种自适应Morlet小波滤波方法及其在滚动轴承早期故障特征提取中的应用[J]. 东南大学学报(自然科学版), 2016, 46(3)： 457-463. Zhang Wan, Jia Minping, Zhu Lin. An adaptive Morlet wavelet filter method and its application in detecting early fault feature of ball bearings[J]. Journal of Southeast University (Natural Science Editions), 2016, 46(3): 457-463. (in Chinese)

[10]唐贵基, 王晓龙. 可调品质因子小波变换在滚动轴承微弱故障特征提取中的应用[J]. 中国电机工程学报, 2016, 36(3)： 746-754. Tang Guiji, Wang Xiaolong. Application of tunable Q-factor wavelet transform to feature extraction of weak fault for rolling bearing[J]. Proceedings of the CSEE, 2016, 36(3): 746-754. (in Chinese)

[11]贺王鹏, 訾艳阳, 陈彬强. 周期稀疏导向超小波在风力发电设备发电机轴承故障诊断中的应用[J]. 机械工程学报， 2016, 52(3)： 41-48. He Wangpeng, Zi Yanyang, Chen Binqiang. Periodic sparsity oriented super-wavelet Analysis with application to motor bearing fault detection of wind turbine[J]. Journal of Mechanical Engineering, 2016, 52(3): 41-48. (in Chinese)

[12] Thanagasundram S, Spurgeon S, Schlindwein F S. A fault detection tool using analysis from an autoregressive model pole trajectory[J]. Journal of Sound and Vibration, 2008, 317(3)： 975-993.

[13]Mainardi L T, Bianchi A M, Baselli G, et al. Pole-tracking algorithms for the extraction of time-variant heart rate variability spectral parameters[J]. IEEE Transactions on Biomedical Engineering,1995, 42(3)： 250-259.

[14] Thanagasundram S, Feng Y H, Schlindwein F S. A case study of autoregressive modelling and order selection for a dry vacuum pump[C]. Twelfth International Congress on Sound and Vibration, 2005： 1-10.

[15]Zhang Y X, Randall R B. Rolling element bearing fault diagnosis based on the combination of genetic algorithms and fast kurtogram[J]. Mechanical Systems and Signal Processing, 2009, 23(5)： 1509-1517.