一个(3+1)维非线性演化方程的周期波解
2018-02-05郭婷婷
郭婷婷
(山西大学 商务学院, 山西 太原 030031)
0 引 言
求解非线性偏微分方程的精确解是研究非线性物理科学的重要组成部分, 现阶段已经求出的精确解有孤立波解, 有理解, 周期波解, negaton解, peakon解, complexiton解等[1-3]. 这些解的获得对非线性物理现象的研究意义重大, 譬如, 精确解中的钟状孤波解可以用来模拟流体动力学中所观测到的波动现象. 这些不同类型的精确解之间也有一定的关系, 可以通过研究解的一致性进而构造新的精确解. 文中涉足高维非线性演化方程, 针对一个非线性(3+1)维演化方程[4]进行研究, 给出其1-周期波解和2-周期波解, 结合该方程的1-孤波解和2-孤波解来研究这两种解的关系, 并进行解的渐近性分析.
M维黎曼theta函数[5]以傅里叶级数的形式定义如下:
式中:β=(β1,β2,…,βM)T∈CM为M维复位移向量;v为M维正定实值对称矩阵;p=(p1,p2,…,PM)T∈ZM为M维整数向量. 其中两个向量的内积运算定义如下: 如果a=(a1,a2,…,aM)T,b=(b1,b2,…,bM)T为2个向量, 那么向量a与b的内积为〈a,b〉=a1b1+a2b2+…+aMbM. 黎曼theta函数具有周期性[6]
L(β+1+v,v)=e-iπv-2πiβL(β,v).
(1)
关于Dx1,Dx2,…,DxM,Dt的双线性算子[7]给出如下
由算子定义可以得出以下运算性质[8]: 假设αj=pjx1+qjx2+…+rjxM+sjt+wj,j=1,2, 则
(p1-p2)a(q1-q2)b…(r1-r2)c(s1-s2)deα1+α2,
(2)
式中:pj,qj…,rj,sj,wj为常数. 这个性质在获取方程的周期波解和双线性表示的构造过程中都起到很重要的作用.
对于(3+1)维非线性演化方程
3ψyy+3ψzz+(ψ3x+6ψψx+ψt)x=0,
(3)
我们可以作对数变换ψ=(2lnH)xx, 并结合双线性算子的关系式[9]
把非线性方程双线性化为
H(x,y,z,t)=0,
(4)
式中:C为积分常数. 根据Hirota双线性方法[10], 如果将H(x,y,z,t)取为δ的幂级数形式H(x,y,z,t)=1+δH1+δ2H2+o(δ2), 代入式(4)中整理关于δ的幂次项, 假设H1=eα,α=ax+by+cz+dt+e, 取δ=1可得出非线性(3+1)维演化方程式(3)的1-孤子解
ψ=2[ln(1+eα)]xx,
α=ax+by+cz+dt+e.
(5)
假设H1=eα1+eα2,αj=ajx+bjy+cjz+djt+ej,j=1,2. 经过一系列代数运算, 可得出非线性(3+1)维演化方程式(3)的2-孤子解

(6)
1 (3+1)维非线性演化方程的1-周期波解
假设一维黎曼theta函数
(7)
是该双线性方程的解, 其中β=fx+gy+hz+lt+m, 那么
由Hirota算子的运算性质式(2), 上式可化为
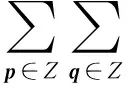


4π2[2q′-(p′-2)]2fl+C}eiπv{q′2+[q′-(p′-2)]2}e2πi(p′-1)v=R(p′-2)e2πi(p′-1)v=0.
当p′为奇数时,R(p′)=R(1)eπi(p′+1)v, 当p′为偶数时,R(p′)=R(0)eπip′v, 那么要使一维黎曼theta函数式(7)是双线性(3+1)维方程式(4)的解, 就要使R(p′)为0, 即
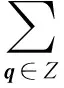
(8)

4π2(2q-1)2fl+C]eiπv·(2q2-2q+1)=0.
(9)
为简单起见, 将式(8)~(9)转化为线性系统
(10)
16π4(2q-1)4f4]η2q2-2q+1,eiπv=η.
为求解以上线性方程组来确定黎曼theta函数中的参数l和积分常量C, 先将线性系统式(10)中的系数矩阵与常数项矩阵的所有元素展开成η的幂级数形式
r11=-32π2fη2-128π2fη8+o(η8),
r12=1+2η2+2η8+o(η8),
(11)
r21=-8π2fη-72π2fη5+o(η5),
r22=2η+2η5+o(η5),
(12)
S1=32π2(3h2+3g2-16π2f4)η2-
128π2(3h2+3g2-64π2f4)η8+o(η8),
(13)
S2=[24π2(h2+g2)-32π4f4]η+
[216π2(h2+g2)-2 592π4f4]η5+o(η5),
(14)
于是线性系统式(10)的各项将可以变形为等价形式
将展开式(11)~(14)代入R(l,C)T=S中, 其中R=(rij)2×2,S=(S1,S2)T, 整理η的相同幂次项得
l1=0, C2=192π2(h2+g2)-640π4f4,
即
C=[192π2(h2+g2)-640π4f4]η2+o(η2),
(15)
于是一维黎曼theta函数式(7)是双线性方程式(4)的解, 其中l和积分常量C由式(15)确定, 而f,g,h,m,v为自由变量. 由黎曼theta函数的周期性式(1)得
β=fx+gy+hz+lt+m,
(16)
是(3+1)维非线性演化方程式(3)的1-周期波解.
2 (3+1)维非线性发展方程的2-周期波解
假设二维黎曼函数
βj=fjx+gjy+hjz+ljt+mj,j=1,2,
(17)
是双线性(3+1)维演化方程(4)的解, 由双线性算子的运算性质式(2)得
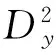
12π2〈p-q,h〉2+16π4〈p-q,a〉4-4π2〈p-q,f〉〈p-q,l〉+C]e2πi〈β,q+p〉+πi(〈vq,q〉+〈vp,p〉)·



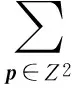
4π2〈2p-η1,f〉〈2p-η1,l〉+C)eπi(〈vp,p〉+〈v(p-η1),(p-η1)〉)=0,
(18)

4π2〈2p-η2,f〉〈2p-η2,l〉+C)eπi(〈vp,p〉+〈v(p-η2),(p-η2)〉)=0,
(19)

4π2〈2p-η3,f〉〈2p-η3,l〉+C)eπi(〈vp,p〉+〈v(p-η3),(p-η3)〉)=0,
(20)

4π2〈2p-η4,f〉〈2p-η4,l〉+C)eπi(〈vp,p〉+〈v(p-η4),(p-η4)〉)=0,
(21)

〈vp,p〉+〈v(p-ηk),(p-ηk)〉=

(12π2〈2p-η1,g〉2+12π2〈2p-η1,h〉2-16π4〈2p-η1,f〉4)ε1(p),
(22)

(23)

(24)

(25)
为求解的方便, 将较复杂的式(22)~(25)转化为线性系统
R(l1,l2,0,C)T=S,
(26)
式中:
R=(rij)4×4,S=(S1,S2,S3,S4)T,


这里ϖ为任意常数. 这样, 可以通过求解线性系统确定积分常量C和黎曼theta函数中参数l1,l2的值, 以确保式(17)是该双线性(3+1)维方程式(4)的解. 分析系数矩阵R, 常数项矩阵S中各个
元素, 注意到η1=(0,0)T,η2=(1,0)T,η3=(0,1)T,η4=(1,1)T, 结合式(22)~(25), 将线性系统式(26)中的各部分记为关于ε1,ε2的幂级数, 形式如下
将以上的3个展开式代入线性系统式(26)并整理关于ε1,ε2的各项系数, 得
C0=C1=C2=C12=0,
那么
w+v≥2,
(27)
(28)
于是二维黎曼theta函数式(17)是双线性方程式(4)的解, 这里积分常量C和lj,j=1,2, 由式(27)~(28)确定,fj,gj,hj,mj为自由变量,v为自由实对称矩阵. 由黎曼theta函数的周期性式(1)并结合对数变换可以得出j=1,2时
βj=fjx+gjy+hjz+ljt+mj,
(29)
是非线性(3+1)维演化方程式(3)的2-周期波解.
3 解的一致性讨论

如果将波的振幅做如下限制, 当εj→0时,j=1,2,

1+(e2πiβ1+e-2πiβ1)eπiv11+(e2πiβ2+e-2πiβ2)eπiv22+[e2πi(β1+β2)+e-2πi(β1+β2)]eπi(v11+2v12+v22)+…=
因此当参数ε1,ε2趋近于0时, (3+1)维非线性方程式(3)的2-周期波解式(29)将趋近于2-孤子解式(6).
综上, 对(3+1)维非线性发展方程式(3)进行分析, 给出其相应的双线性表示式(4), 1-孤子解式(5)和2-孤子解式(6). 结合黎曼theta函数的周期性质, 给出方程(3)的1-周期波解(16)式和2-周期波解(29)式, 并在限制波的振幅条件时, 对周期波解进行了渐近性的分析, 得出当参数η趋于0时, 该方程的1-周期波解式(16)将趋于1-孤子解式(5), 当参数ε1, ε2趋近于0时, 该非线性方程的2-周期波解式(29)将趋于2-孤子解式(6).
[1]陈登远. 孤子引论[M]. 北京: 科学出版社, 2006.
[2]GuoFK,FengBL,GuoTT.Afewnotesonlaxintegrability,integrablecouplingsandcomputingformulaoftheconstantr[J].JournalofAppliedNonlinesrDynamics, 2012, 1(4): 401-406.
[3]ZhangYF,HonYC.Someevolutionhierarchiesderivedfromself-dualYang-millsequations[J].CommunicationsinTheoreticalPhysics, 2011, 56(5): 856-872.
[4]郭冠平.(3+1)维非线性方程新的精确解[J].四川师范大学学报, 2002, 25(2): 159-163.GuoGuanping.Thenewexactsolutionsof(3+1)dimensionsnonlinearequations[J].JournalofSichuanNormalUniversity, 2002, 25(2): 159-163. (inChinese)
[5]FanEG,HonYC.QuasiperiodicwavesandasymptoticbehaviorforBogoyavlenskii’sbreakingsolitonequationin(2+1)dimensions[J].PhysicalReviewE, 2008, 78(3): 036607(13).
[6]TianSF,ZhangHQ.Riemannthetafunctionsperiodicwavesolutionsandrationalcharacteristicsforthenonlinearequations[J].JournalofMathematicalAnalysisandApplications, 2010, 371(2): 585-608.
[7]HirotaR.Thedirectmethodinsolitontheory[M].NewYork:CambridgeUniversityPress, 2004.
[8]ZhangYF.Liealgebrasforconstructingnonlinearintegrablecouplings[J].CommunicationsinTheoreticalPhysics, 2011, 56(5): 805-812.
[9]郭婷婷. (2+1)维KdV方程的Bäcklund变换和无穷守恒律[J]. 中北大学学报(自然科学版), 2017, 38(3): 277-281.GuoTingting.TheBäcklundtransformationandinfiniteconservationlawsofthe(2+1)dimensionalKdVequation[J].JournalofNorthUniversityofChina(NaturalScienceEdition), 2017, 38(3): 277-281. (inChinese)
[10]郭婷婷. (2+1)维KdV方程的孤子解和新行列式解[J]. 中北大学学报(自然科学版), 2015, 36(2): 118-121.GuoTingting.Thesolitonsolutionsandthenewwronskiandeterminantsolutionsofthe(2+1)dimensionalKdVequation[J].JournalofNorthUniversityofChina(NaturalScienceEdition), 2015, 36(2): 118-121. (inChinese)
