火箭武器发射箱结构优化方法及应用
2018-02-05杨翠东鄢章渝
杨翠东, 鄢章渝, 韩 磊, 赵 鑫, 李 军
(1. 南京理工大学 机械工程学院, 江苏 南京 210094; 2. 中国兵器工业导航与控制技术研究所, 北京 100089)
0 引 言
发射箱是火箭武器系统的重要组成部分, 它与起落架相连, 箱中的导轨用作滑移导引部, 火箭弹平时固定在其上. 火箭武器通过使用发射箱可以使多种火箭弹或火箭弹和导弹共架发射, 实现一箱多用、 一架多用的目标[1]. 在发射和装填等状态下, 发射箱承受着火箭弹重力对它的动态作用和燃气射流压强对它的冲击, 故其需要有较好的刚度和足够的强度以保障发射的安全和精度, 同时其质量还需尽可能小.
发射箱的结构大多是在借鉴现有类似结构和工程设计经验的基础上设计出来的, 它遵循的是设计、 工程分析、 再设计(或称优化)、 加工装配和试验验证等流程. 如文献[2]采用经验设计方法对发射箱各个部分进行了详细设计; 宋时浩[3]对某型(储)运发射箱不同工况下的性能表现进行了分析. 实际工程设计中, 发射箱结构往往比较保守, 造成结构的冗余和材料的浪费. 特别地, 当发射箱需承载大质量(达到数吨)火箭弹时, 其刚强度等设计问题的难度比较大, 因此对发射箱的结构优化有着重要的工程意义.
目前, 很多学者和工程师从实践出发解决了许多领域的结构优化问题, 如王国春等[4]在考虑弯曲、 扭转、 顶压、 正碰和侧碰等多种工况下, 对某型车白车身进行了拓扑优化, 提出了基于渐进空间的白车身传力路径规划方法; 胡朝辉等[5]提出了基于区间分隔的车架拓扑优化方法和流程; 张明等[6]提出了优化驱动的飞机起落架结构设计方法; 文献[7]对重型压力机机架采取分阶段的拓扑优化方法, 成功得到了更轻的结构. 但在火箭武器领域, 发射箱的结构优化还没有完整的方法和步骤可循, 有待进一步探索.
本文研究的发射箱搭载的火箭弹弹重大, 利用适配器以同时离轨方式发射, 这导致发射箱滑轨分成高度不同的两部分. 低轨变形对火箭弹装填和发射影响较大, 因此需在保证箱体强度的同时, 保证低轨的刚度. 为解决该问题, 本文提出了基于结构优化理论和有限元分析方法的火箭炮发射箱设计方法和思路.
1 发射箱拓扑优化
1.1 发射箱初始几何模型
根据已知的滑轨长度、 火箭弹尺寸、 定向钮导槽和插拔机构安装槽尺寸、 适配器滑轨以及发射箱最大外形限制尺寸建立某火箭炮发射箱的初始几何模型, 具体组成和方位如图 1 所示. 其中, 锁紧孔和连接板为发射箱与火箭炮起落架连接定位的辅助构件, 高轨和低轨合称为下轨.

图 1 带弹发射箱装配模型Fig.1 Missile launcher assembly model
1.2 发射箱有限元模型
在HyperMesh中采用六面体单元对各部件进行网格划分, 除配重火箭弹外, 平均网格尺寸约为20 mm. 配重火箭弹质量为3 t, 质心位置、 转动惯量等参数与实际近似; 实际中有后、 中、 前定心部且前定心部在适配器上方, 在此略去前定心部. 为了更好地传递载荷, 在特定区域设置了网格过渡, 整个模型共608 166个单元和679 929个节点. 图 2 所示为带弹发射箱有限元网格模型.

图 2 带弹发射箱网格模型Fig.2 Mesh model of missile launcher
优化计算所使用的材料模型均为线弹性, 适配器材料为铝, 密度为2.70×10-9t/mm3, 弹性模量为68 000 MPa, 泊松比为0.34; 其它部分采用钢材料, 密度为7.83×10-9t/mm3, 弹性模量为208 000 MPa, 泊松比为0.28, 配重火箭弹密度为1.64×10-9t/mm3.
1.3 工况处理
发射箱在实际条件下主要有5种工况: 行军工况、 发射工况、 吊装工况、 装填工况和堆放工况. 在拓扑优化前无法预知带弹整箱的重量, 故不考虑堆放工况; 火箭弹平放(0°射角)时重力分量最大, 装填(或推弹)对发射箱刚度要求最高, 故考虑火箭弹装填工况; 实际火箭弹发射时弹尾喷管产生的燃气射流会对发射箱有严重的冲击, 发射箱内壁要受到燃气压强的作用, 故发射工况须考虑在内; 除此之外, 还考虑了吊装工况.
选取7个位置模拟火箭弹运动过程中对发射箱的作用, 7个位置的火箭弹、 适配器与下轨的相对关系如图 3 所示.

图 3 7个位置火箭弹与发射箱相对关系Fig.3 The seven relative positions betweenthe rocket and launching canister
发射箱下轨可简化认为由后、 中、 前3段梁构成, 在两锁紧孔处隔开. 火箭弹的重力主要通过后定心部、 适配器传递给下轨, 火箭弹质心位于后定心部和适配器之间, 后定心部到质心的距离为适配器到质心的距离的2倍. 在位置1处简化认为低轨悬臂长度最大, 对低轨的刚度要求最高; 位置5为中定心部与高轨前端对齐的状态, 在实际装填和不同射角的发射状态下存在中定心部与高轨碰撞的可能; 火箭弹在位置7处装填到位, 高轨后端可简化认为处于悬臂状态, 此位置对高轨后端刚度要求较大. 为了更好地捕捉到低轨和高轨的材料布局形式, 在位置1和位置5之间间隔近似相等距离选取了3个位置, 即位置2~4; 为了捕捉低轨根部靠近锁紧孔处的材料分布, 在位置5和7之间选取了位置6.
位置1~6的边界条件均为锁紧孔下端面固定, 位置7处边界条件为固定发射箱顶端与锁紧孔在同一轴向(X方向)位置处的4个吊点, 用于模拟吊装工况, 两种不同的边界条件如图 4 所示. 重力加速度大小为9 803 mm/s2, 方向为负Z方向.

图 4 工况边界条件Fig.4 Boundary conditions
火箭弹发射过程中, 喷管以外燃气射流流场的压强分布(压强场构型)不随火箭弹的运动变化, 即分布相对喷管是保持不变的. 这样, 火箭弹在发射箱内运动时, 燃气射流流场就像一个火箭弹带着一条尾巴, 这条尾巴的外边界滑过箱子内壁, 那么壁面上感受到的压强分布也可以想象成运动的. 压强场分布由流体力学Fluent计算得出, 靠近箱口处的值较大. 图 5 所示为火箭弹弹尾离开发射箱低轨时的燃气压强分布, 压强幅值为0.15 MPa.
弹尾离开低轨时燃气压强作用在发射箱内壁上的面积最大, 火箭弹已离轨, 其重力对下轨无作用, 但经过试算, 仅压强作用下所得拓扑优化结果的材料分布不清晰, 为获得清晰结果, 虚拟地让火箭弹在位置5处, 如图 5 所示. 而发射过程中, 弹在位置1时压强对箱体作用开始凸显, 如图 6 所示. 这两种压强作用下的边界条件均为锁紧孔下端面固定.

图 5 弹尾离开发射箱时内壁压强分布(情况一)Fig.5 The distribution of pressure on the inner wall for missile away from launching canister (condition one)
适配器和火箭弹、 适配器和低轨、 后定心部和高轨、 连接板和发射箱下端、 锁紧孔和连接板均为绑定(TIE)关系.

图 6 位置1发射箱内壁压强分布(情况二)Fig.6 The pressure of the inner wall on position 1 (condition two)
1.4 发射箱拓扑优化控制参数
拓扑优化实质是在给定的设计区域内寻求最优的材料分布, 即材料的去留问题(0~1分布). 对于连续结构拓扑优化问题, 最常用的方法为密度法[8], 其将单元密度定义为0和1, 优化过程中采用密度斜率控制法, 引入惩罚因子p来抑制中间密度产生.p的选取与原材料的泊松比有关, 只要p值足够大(一般μ=0.3时, 要求p≥3), 中间密度值就能被惩罚趋于0或1[9]. 对于三维结构, 具体表达如下
(1)
OptiStruct优化软件采用可分离凸近似对偶算法求解拓扑优化问题. 本文定义了17个设计区域体积分数约束条件, 其下限值均为0.1, 上限值均为0.3. 设定下限值是希望各个区域都能有材料保留且使载荷在设计区域内传递顺畅, 而设定上限值则可使每个区域的材料不过多. 9个拓扑优化模型的约束条件均相同, 目标函数均定义为设计区域应变能之和最小(刚度最大化).
拓扑优化数学模型[10]如下
(2)
式中:C为应变能;U和F分别为节点位移和力向量;K为全局刚度矩阵;ke和k0分别为第e个单元的刚度和材料的初始刚度;ρe为第e个单元的相对密度;p为惩罚因子;Vni,Vn0分别为编号为n的设计区域第i个迭代和初始迭代时的体积.
为了得到预期的拓扑优化结果, 以高轨、 低轨过渡处为分界将发射箱分为17个设计区域. 火箭弹、 适配器、 锁紧孔和连接板、 起导引作用的单元为非设计区域. 设计区域编号和非设计区域如图 7 所示. 为得到清晰且利于加工制造的结果, 对各设计区域定义了制造约束, 如表 1 所示. 挤压约束利于得到贯穿挤压路径的支撑板或梁结构几何特征, 模式重复约束使发射箱拓扑优化结果左右(关于XOZ面)对称.

图 7 设计区域编号和非设计区域Fig.7 Number of design domains and non design domains

区域编号最小成员尺寸/mm最大成员尺寸/mm挤压约束路径方向模式重复备注160120Z方向主域从域为2360120Z方向主域从域为4560120Y方向主域从域为6760120Y方向主域从域为8960120Y方向主域从域为101160120Y方向主域从域为121360120Z方向--1460120Z方向主域从域为161560120Z方向--1760120Z方向--
1.5 发射箱拓扑优化结果分析
拓扑优化结果可以帮助寻找最佳传力路径, 为发射箱结构设计提供概念性参考方案. 拓扑优化结果密度阈值均取为0.3, 即只保留相对密度大于0.3的单元. 此时, 去除了对承载无较大贡献的单元, 且保证结果中材料分布连续, 传力路径清晰, 利于发射箱几何重构的进行. 如图 8 所示, 为看清内部, 结果中未显示区域1、 3和配重火箭弹.


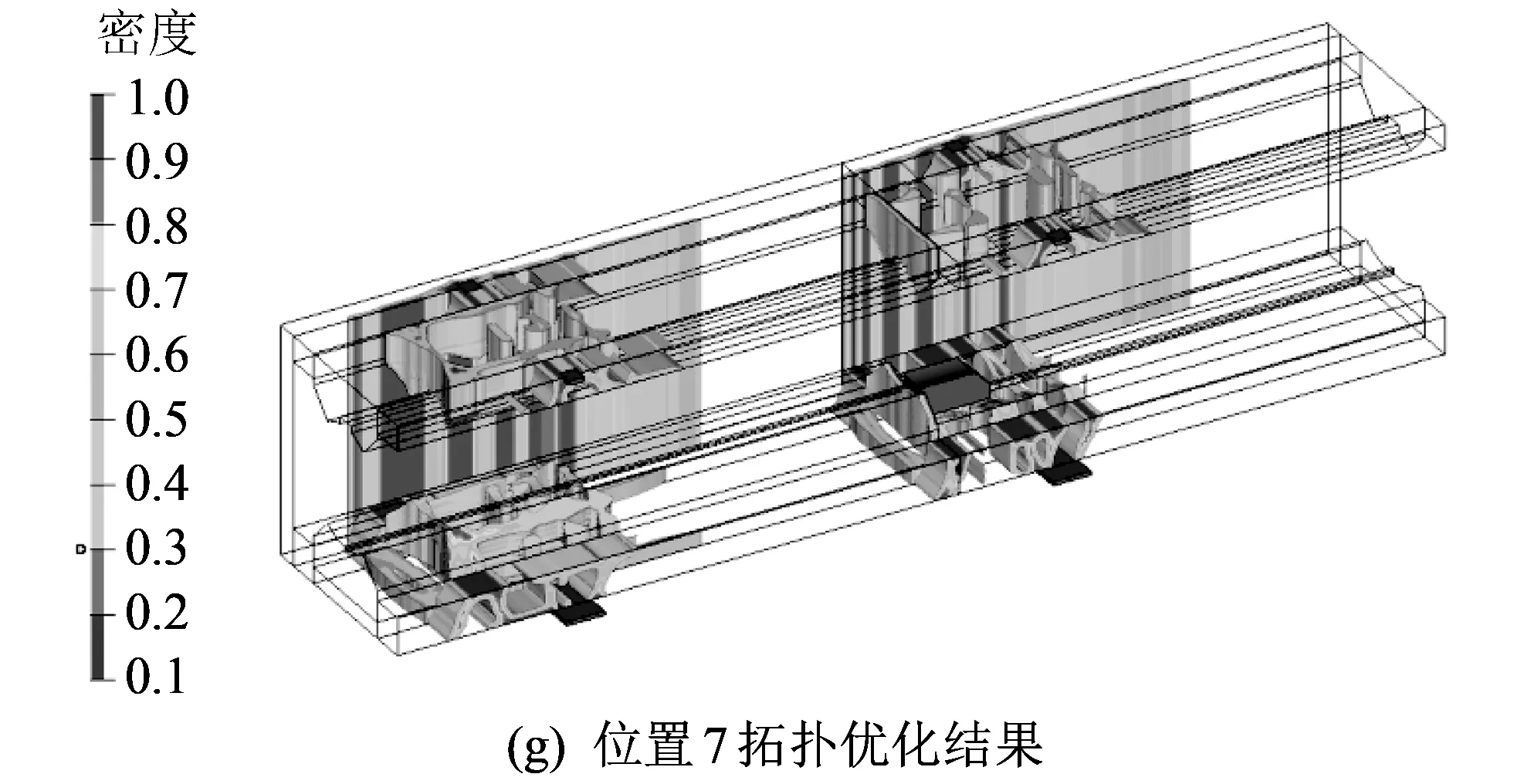
图 8 7个位置拓扑优化结果Fig.8 The topological optimization results of seven positions
可以看出7个位置下的区域1、 2、 3和4均为类似蒙皮的结构, 区域5、 6、 7和8在两处锁紧孔附近均有相似的梁结构特征. 适配器前端的材料被去除, 原因在于适配器下端及后定心部下方传递火箭弹重力的区域有足够材料支撑.
7个位置下的区域9、 10、 11和12材料都较少且基本保持不变, 说明这些区域在各位置下承载贡献小. 区域14、 16在后锁紧孔处变化不大, 靠近力作用位置渐出现规则的板状结构; 适配器在位置3、 4和5时, 力的作用位置在这些区域的中间, 这些区域的材料集中于后锁紧孔和后定心部附近, 此时区域14、 16有规则清晰的板状结构.
区域15在前锁紧孔附近均有相同的支撑板状结构, 其位于适配器下方的子区域也有支撑板结构, 其中间部分随适配器位置的变化有材料连接趋势. 区域17的材料承载贡献小且集中在前锁紧孔附近, 有零星板状结构. 吊装工况下, 位置7所有区域的材料基本上集中在两锁紧孔附近.
7个位置的叠加结果如图 9 所示, 得到了发射箱仅受火箭弹重力动态作用的材料基本布局, 但不能反映燃气射流压强作用下发射箱侧向材料分布. 1.3节所述两种压强下的拓扑优化结果如图 10 所示, 可以看出侧向区域1、 2、 3和4材料形式为梁结构.

图 9 7个位置叠加拓扑优化结果Fig.9 Superposed topological optimization result of seven positions

图 10 压强作用下拓扑优化结果(上为情况一、 下为二)Fig.10 The topological optimization result under the pressure
2 发射箱几何重构及验证
发射箱拓扑优化结果并非工程实际中能直接实现的设计方案, 须加以工程解读. 借助CAD软件重新构建发射箱几何模型, 如图 11 所示. 发射箱的焊接结构较多, 主要结构形式为板、 梁结构. 区域13、 14和15构成发射箱下轨, 依据优化结果中材料分布趋势, 确定该区域贯穿发射箱全长的两道纵梁, 区域13靠近前锁紧孔的位置增加45°斜梁; 这3个区域也有厚度为6 mm的等间距板结构, 斜梁附近板厚为16 mm, 锁紧孔附近板厚为10 mm. 区域2、 4为厚度3 mm蒙皮结构外加8道竖梁, 区域5、 7、 9、 11主要为矩形梁和斜板支撑结构, 矩形梁和竖梁位置对齐, 锁紧孔位置处建立锁紧梁, 起支撑纵梁和连接作用. 新发射箱总质量为3.25 t.
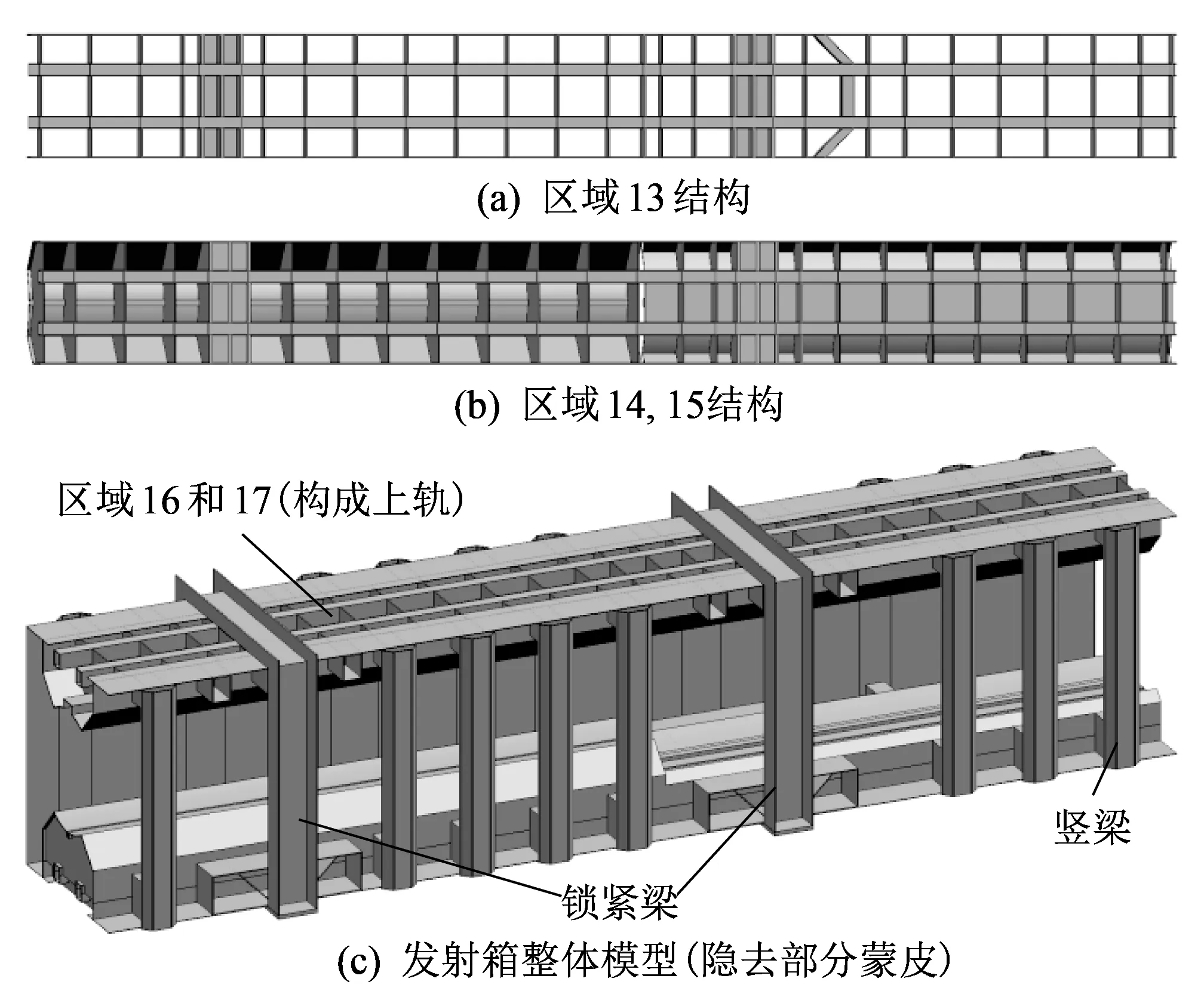
图 11 发射箱新几何模型Fig.11 New launching canister model
在发射箱几何重构过程中去除了与分析无关的细小特征, 并结合实际加工制造要求做了相应调整. 建立新发射箱有限元模型, 如图 12 所示.
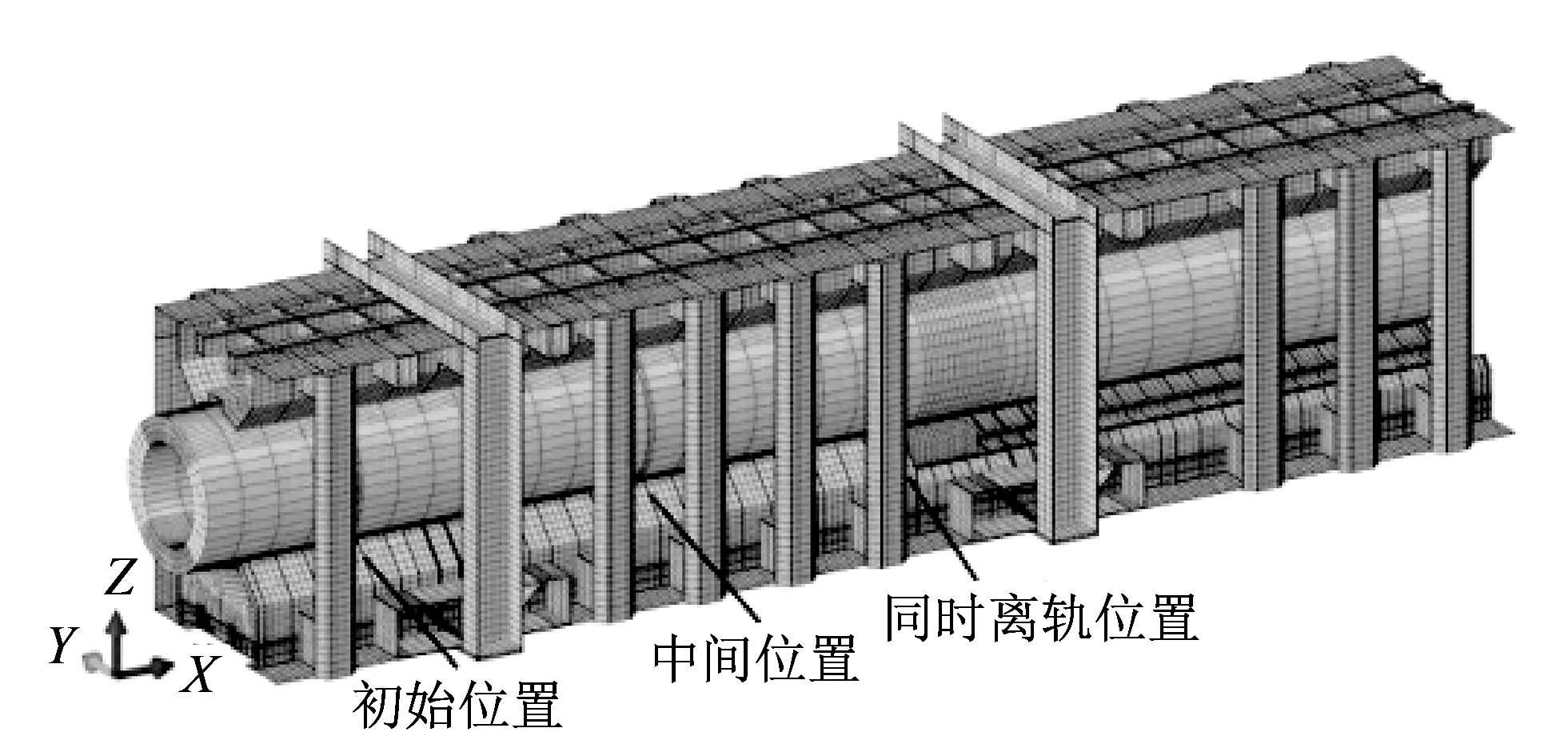
图 12 新发射箱有限元模型Fig.12 New finite element model of launching canister
图12中所指位置均为后定心部对应所在位置, 适配器随着后定心部位置的变动而变动到相应位置. 对其0°射角发射工况进行有限元动力学分析, 结果表明, 火箭弹运动到不同位置时, 位移较大的地方主要在后定心部下方、 支撑板跨度中心或适配器下方; 同时分析1.3节两种压强分布下发射箱侧向(Y方向)位移, 典型工况结果见表 2.

表 2 优化后发射箱新模型分析结果
发射箱采用的材料主要为具有良好焊接性能的HJ58钢(屈服强度为450 MPa)及510L钢板(屈服强度为345 MPa). 由分析结果可知, 主要危险工况下的应力、 位移结果都能满足工程要求, 且发射箱尺寸参数还存在优化空间.
3 发射箱形状优化
新结构中发射箱上轨、 下轨支撑板数量比较多, 除去锁紧孔附近支撑板, 总质量为0.44 t, 可进一步优化支撑板的厚度以减轻整个发射箱的重量.
考虑火箭弹重力的动态效应, 采用与1.3节类似的方法, 选取9个位置进行静态优化计算, 见图 13, 图中所指位置均为后定心部对应所在的位置, 其中, 位置9为火箭弹同时离轨位置. 由于燃气压强对发射箱横向(Y方向)变形影响大, 对发射箱垂向(Z方向)变形影响不大, 故在这9个位置处均忽略燃气压强作用, 仅考虑火箭弹重力作用.

图 13 计算位置示意Fig.13 Calculating positions
采用形状优化的方法将支撑板厚度转化为形状变量, 优化支撑板的边界节点位置. OptiStruct使用扰动向量法[10]来控制网格的变形, 将网格节点位置的扰动定义为形状变量, 实现支撑板厚度的变化. 14个形状设计变量如图 14 所示.
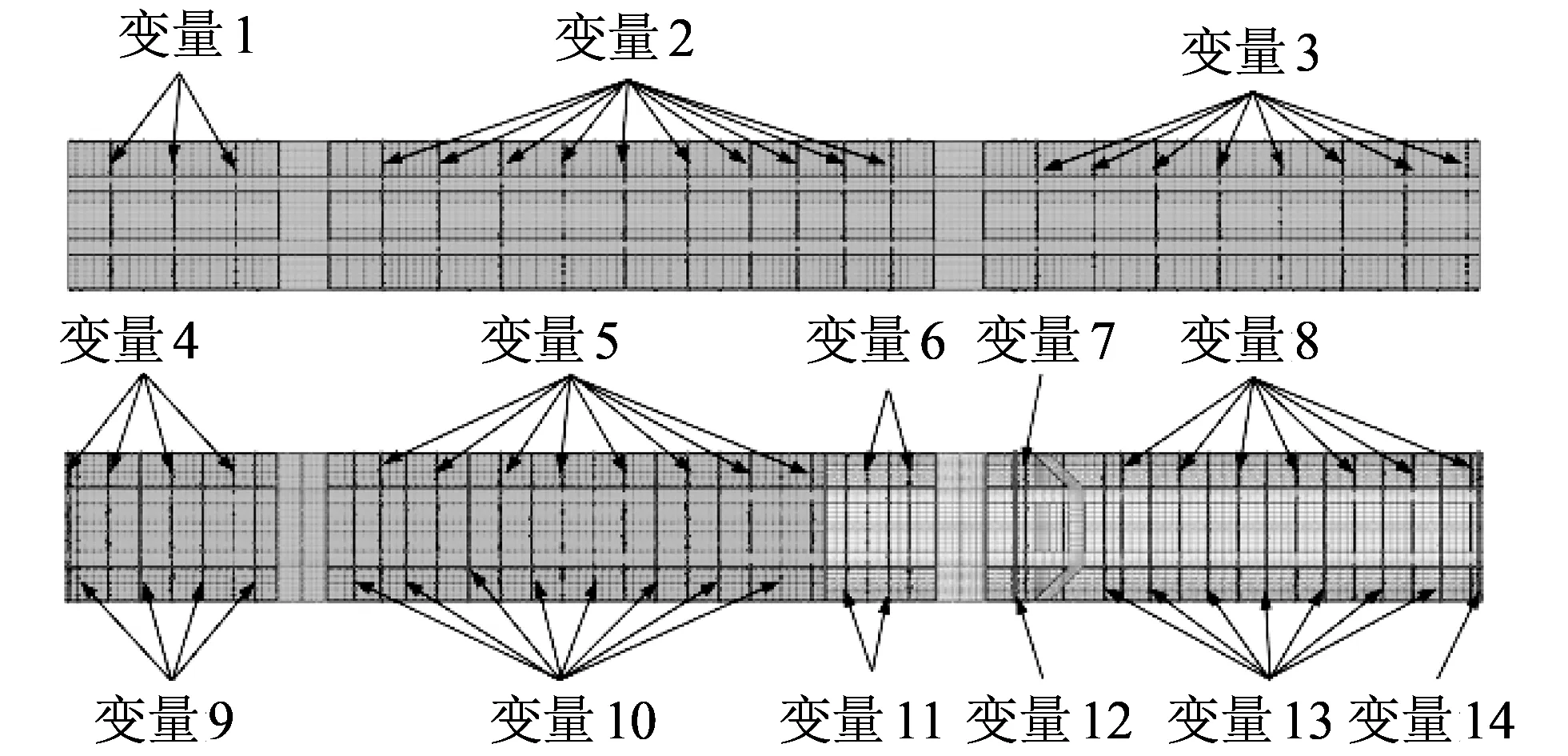
图 14 形状设计变量编号Fig.14 Shape design variable numbers
形状变量设计区间见表 3.

表 3 形状变量设计区间
以支撑板的质量之和最小为目标函数, 约束后定心部下方、 支撑板跨度中心位移下限值为-0.25 mm(负号代表Z负方向)及适配器下方位移下限值为-0.90 mm. 9个位置的计算结果都经过6个迭代步收敛, 支撑板质量之和由0.44 t降至0.29 t. 最终得到的支撑板厚度值为9个位置计算结果的交集, 见表 3.
支撑板形状优化设计后的有限元分析结果表明, 同时离轨位置最大应力为186 MPa, 最大位移为0.86 mm, 仍能满足工程要求, 达到了减重的目的.
4 结 论
本文针对火箭武器发射箱传统设计方法的不足, 结合现代结构优化设计技术, 实现了发射箱结构从无到有的设计. 通过以上研究可得出结论:
1) 发射箱所受工况较为复杂, 通过拓扑优化可有效模拟其载荷作用情况, 寻找最优传力结构, 从而减少了产品设计过程中的某些盲目性, 可大大缩短其设计研发周期.
2) 与传统设计方法所得原结构相比, 新结构质量2.96 t较原结构质量3.39 t减轻了12.7%, 且最大位移由1.87 mm减小至0.86 mm, 刚度显著提高.
3) 本文形成了基于结构优化理论和有限元分析方法的火箭炮发射箱设计方法和思路, 如图 15 所示. 其在理论和实践上阐述了发射箱结构优化设计方法和应用问题, 可为火箭武器领域相关部件设计及一般机械领域的结构设计提供参考.
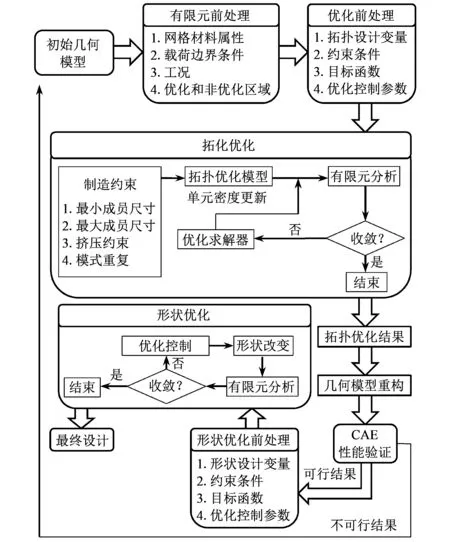
图 15 发射箱设计方法和思路Fig.15 Design method and idea of launching cansiter
[1]于存贵, 李志刚. 火箭发射系统分析[M]. 第1版. 北京: 国防工业出版社, 2012.
[2]吴媛. 贮运发射箱结构设计及有限元分析[D]. 成都: 电子科技大学, 2009.
[3]宋时浩. 某(储)运发箱安全性能分析[D]. 南京: 南京理工大学, 2014.
[4]王国春, 段利斌, 陈自凯, 等. 基于渐进空间拓扑优化技术的白车身传力路径规划方法[J]. 中国机械工程, 2015, 26(20): 2827-2834. Wang Guochun, Duan Libin, Chen Zikai, et al. A novel approach for vehicle body force path planning based on progressive spatial topology optimization[J]. Journal of Chinese Mechanical Engineering, 2015, 26(20): 2827-2834. (in Chinese)
[5]胡朝辉, 张健, 李光耀, 等. 基于区间分隔的卡车车架轻量化设计[J]. 中国机械工程, 2016, 27(8): 1130-1135. Hu Zhaohui, Zhang Jian, Li Guangyao, et al. Lightweight design of truck frame based on interval partition[J]. Journal of Chinese Mechanical Engineering, 2016, 27(8): 1130-1135.(in Chinese)
[6]张明, 刘文斌, 李闯, 等. 优化驱动的起落架结构设计方法[J]. 航空学报, 2015, 36(3): 857-864. Zhang Ming, Liu Wenbin, Li Chuang, et al. Structural design method of optimized driving landing gear[J]. Journal of Aeronautics, 2015, 36(3): 857-864.(in Chinese)
[7]Zhao X, Liu Y, Hua L, et al. Finite element analysis and topology optimization of a 12000KN fine blanking press frame[J]. Structural and Multidisciplinary Optimization, 2016, 54(2): 375-389.
[8]Bendsøe M P, Sigmund O. Material interpolation sch-emes in topology optimization[J]. Archive of Applied Mechanics, 1999, 69(9): 635-654.
[9]Zhou M, Shyy Y K, Thomas H L. Checkerboard and minimum member size control in topology optimization[J]. Structural & Multidisciplinary Optimization, 2014, 21(2): 152-158.
[10]苏胜伟. 基于Optistruct拓扑优化的应用研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.
[11]Li C, Kim I Y, Jeswiet J. Conceptual and detailed design of an automotive engine cradle by using topology, shape, and size optimization[J]. Structural and Multidisciplinary Optimization, 2015, 51(2): 547-564.
