降雨触发浅层坡体失稳的迟滞现象及其与土质参数的关联性

张建，李江腾，林杭，黄旻鹏，常瑞芹



降雨触发浅层坡体失稳的迟滞现象及其与土质参数的关联性

张建，李江腾，林杭，黄旻鹏，常瑞芹

(中南大学资源与安全工程学院，湖南 长沙，410083)

定义因降雨作用，坡体在降雨结束之后出现最不稳定状态(或滑坡)的现象为迟滞现象。根据雨水在土体中的入渗规律，给出2类降雨作用边坡的雨水入渗模型，以说明降雨触发边坡失稳迟滞现象的发生机理。定义临界时间概念。基于渗流−坡体稳定性耦合分析方法，采用数值分析手段研究迟滞现象与坡体土质参数的关联性。研究结果表明：迟滞现象与土体的渗透参数和强度参数均有关联；当渗透系数s大于1×10−4 m/s，且进气排水能力较强时，土质坡体倾向于在降雨过程中失稳，当s在1×10−7~1×10−6 m/s范围内取值时，坡体的临界时间通常在降雨结束后取得；当土体强度参数一定时，随土体渗透能力增强，坡体的临界时间呈现出不断减小并最终趋于平缓的变化趋势；当土体渗透性一定时，随着土体强度参数增大，坡体的临界时间呈现出不断增大并最终趋于平缓的变化趋势；土体渗透性对迟滞现象的产生有主导作用，在满足渗透性条件下，土体强度参数对迟滞现象产生的影响在土体强度较低时起主导作用。

边坡；降雨；迟滞现象；土体渗透性；土体强度

滑坡灾害发生频繁，降雨是触发边坡失稳的最主要因素[1−3]。根据降雨条件、地势环境、土质类别的不同，降雨产生的雨水有26%~60%入渗到土体中[4]。入渗的雨水将引起坡体浅层土体含水率、孔隙水压力、地下水位等参数发生变化，会导致潜在滑坡体抗滑力与下滑力失衡，进而导致边坡失稳[5−6]。在降雨触发滑坡过程中，从降雨入渗到土壤含水率及孔隙水压力的变化，再到土体强度降低，地下水位上升，整个过程随时间逐步发生。在特定的降雨环境及土质条件下，降雨发生时间与坡体失稳时间存在时间差[7]。在工程实际中，一些边坡通常在降雨结束一段时间后发生滑坡，意味着降雨对滑坡的作用有迟滞现象。降雨触发滑坡的迟滞现象较普遍，如铁路路基在遭受大雨后的第5天发生滑坡事故，造成火车出轨[8]；黄土质边坡在雨季通常较稳定，但在雨季过后可能发生滑坡事 故[9]。因降雨触发滑坡迟滞的时间不一样，使经历降雨后的边坡具有较大潜在危险性，对降雨触发边坡失稳迟滞现象进行分析，有助于进一步了解降雨触发滑坡的致灾机理及对该类灾害的预警控制。关于对降雨触发滑坡滞后现象的研究，RAHARDJO等[10]在研究降雨过程中地下水位及土质特性与边坡稳定性的关联性时发现特定的降雨条件及土质参数情况下，匀质土坡及分层土坡均会发生滑坡滞后于降雨过程的现象，但未进行进一步分析。DOU等[11]基于G-A入渗模型建立了匀质土坡雨水重分布模型，在此基础上从雨水入渗重分布角度阐释了滑坡失稳滞后的原因。DOU 等[12]提出考虑土壤饱和渗透系数空间变异性的边坡稳定分析方法，基于此方法研究了前期降雨持时、土壤饱和渗透系数变异性与降雨触发边坡失稳滞后时长的关联性。降雨触发滑坡滞后现象涉及多因素、多过程，不仅与降雨参数、边坡所处地势环境、雨水入渗过程、边坡失稳过程等相关联，而且与边坡自身的土质参数相关。对于相同降雨环境与地势环境，不同土质的边坡对于降雨触发边坡失稳滞后时长的表现也可能不尽相同。为此，本文作者对雨水入渗规律进行分析，给出简化的雨水入渗分布模型，研究因降雨导致的滑坡滞后于降雨过程的发生机理，再基于渗流−坡体稳定性耦合分析方法，分析土体渗透参数与土体强度参数及迟滞现象的关联性。

1 雨水入渗规律

在理想状态下，雨水入渗过程中浅层土体在竖直方向会呈现渐变特征，即干燥状态、非饱和状态、饱和状态(包含暂态饱和状态)交替出现。在降雨开始之前，表层土体处于干燥状态(初始含水率相对较低)，潜水位以下土体处于饱和状态，因土体毛细作用，潜水位以上小范围内的土体处于非饱和状态，该情形下土体的干湿状态如图1(a)所示。在降雨过程中，表层土体将处于暂态饱和状态，往下依次为非饱和区域、干土区域、非饱和区域及饱和区域(潜水位以下)，如图1(b)所示。当降雨结束一段时间后，表层土体会因入渗及蒸发作用变为干燥状态，潜水位会因雨水入渗而上升，在潜水位以上局部区域分布着非饱和土区域，如图1(c)所示。

(a) 降雨前；(b) 降雨过程中；(c) 降雨后

根据图1所示的土体状态分布规律，建立2类降雨作用边坡雨水入渗模型，用于说明降雨触发边坡失稳迟滞现象的发生机理。图2(a)所示为匀质土坡模型，图2(b)所示为覆土岩质坡体模型。图2中，B1，B2，B3和B4表示随降雨持续，雨水入渗产生的湿润锋向土体深部推移的轨迹(按时间先后顺序)；R1，R2，R3和R4表示降雨结束后浅层土体暂态饱和区域随时间推移逐渐消散的轨迹。降雨触发滑坡需要2个基本条件：1) 充足的降雨，以保证土体中暂态饱和区的产生及发展，降雨量通常用降雨强度与降雨持续时间2个指标来表征；2) 适宜的土壤渗透率，通常用饱和渗透系数及土水特性来表征。对于匀质坡体(见图2(a))，假设满足降雨触发滑坡的2个基本条件，滑坡滞后于降雨过程的现象倾向于在如下情形下发生：降雨结束前，湿润锋发展至轨迹B2或者B3处；降雨结束时，湿润锋发展至轨迹B4，浅层土体暂态饱和区域逐渐消散至轨迹R2或者R3处，此时，潜在滑移面位置处于暂态饱和状态。在雨水作用下，潜在滑移面附近土体含水率增大，孔隙水压力由负压状态变为正压状态，导致土体强度降低，坡体最不稳定状态(或者滑坡)将在此时发生。岩土混合质坡体(见图2(b))与匀质坡体略有不同，主要体现在：1) 地理结构不同，与匀质坡体情形相比较，覆土岩质坡体存在岩土接触界面；2) 雨水入渗路径不同，在降雨量充足情况下，入渗雨水可能沿岩土接触面向坡脚处集流，此时潜在滑移面将在岩土接触面产生。根据不同覆土类型，坡体破坏失稳的类型也不相同，若覆土为松软颗粒土，则岩土接触处的土体液化是剪切破坏所致坡体失稳的主要原因[13−14]。

2 渗流−坡体稳定性耦合分析方法

基于达西定律的二维渗流广义微分方程的表达式如下：

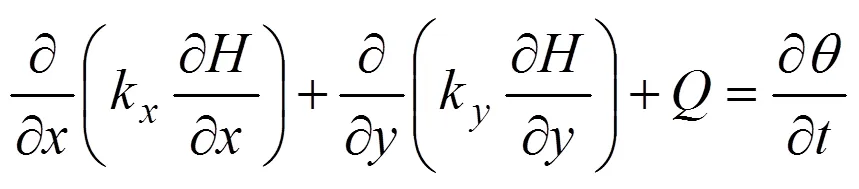
式中：k与k分别为水平方向与竖直方向的渗透率；为总压力水头；为额外施加的边界流量；为体积含水率；为时间。在静态条件下，土壤孔隙中的水处于非流动状态，式(1)等号右侧取0。在非静态条件下，孔隙水在净法向力(n−a)与基质吸力(a−w)作用下产生流动[15−16]。假设不考虑大气压力的变化及孔隙气压力(u)的变化，净法向力(n−a)可以视为常量，不会对土壤体积含水率的变化产生影响，仅有基质吸力(a−w)对土壤中水分运移产生影响，其中主导影响因素为孔隙水压力w。基于以上假设，土壤体积含水率的变化与土壤孔隙水压力的变化可用下式表征：

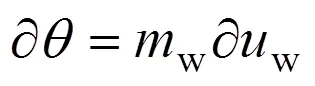
式中：w为土水特性曲线的斜率。孔隙水压力可以进步表示为

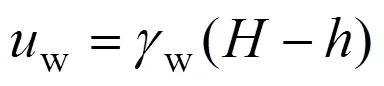
将式(4)代入式(1)得

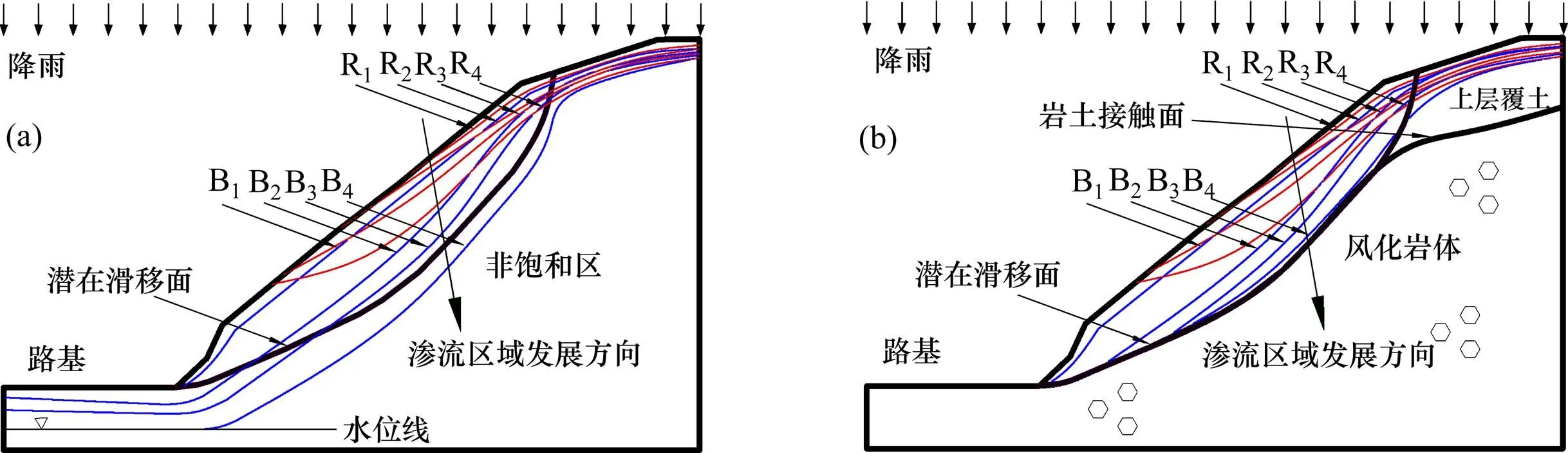
(a) 匀质土坡模型；(b) 覆土岩质坡体模型

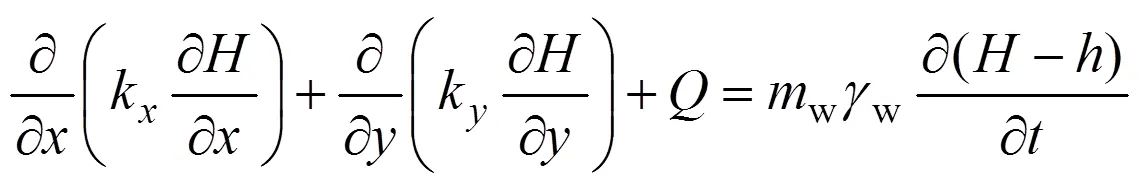
因式(5)中高程为常量，在求偏导过程中可以舍弃，进一步化简式(5)得

基于式(6)的二维渗流微分方程涉及土水特性曲线(SWCC)斜率，土水特性曲线通常以基质吸力(a−w)与标准化的体积含水率w之间的函数关系来表征，w的表达式如下：

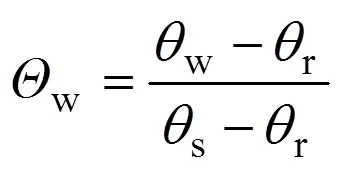
式中：w为特定基质吸力条件下土壤体积含水率；s为饱和体积含水率；r为残余体积含水率。基于下式拟合土水特性曲线[17]：

式中：()为相关系数，计算中取值为1；参数，和分别与土壤空气进入值、土水特性曲线斜率、残余含水量相关联，为自然常数。基于土水特性曲线，采用下式估算土壤渗透曲线[18]：

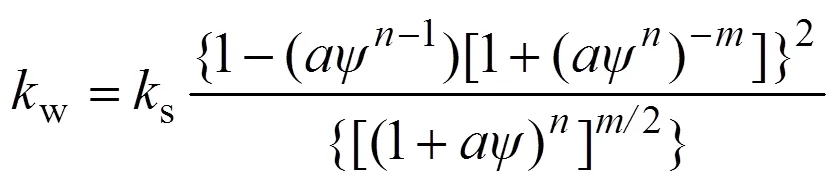
式中：w与s分别为土体渗透系数与饱和渗透系数；=1/(1−)。本次分析中不考虑土体渗透系数的各向异性，即式(6)中k=k=w。

基于式(6)计算设定边界条件下边坡土体中不同时间的渗流场，再基于下式计算非饱和土体抗剪强度：

3 计算模型及参数

3.1 计算模型

采用数值分析方法进行渗流−坡体稳定性耦合分析。渗流分析在SEEP/W中进行(不考虑坡面集流作用)，坡体稳定性在SLOPE/W中进行。将SEEP/W中获得的渗流场数据导入SLOPE/W中进行极限平衡法计算，获得不同降雨时间坡体的安全系数。基于文献[19]，分析过程中采用的数值模型及边界条件如图3所示(图3中，表示初始水位线位置)。有限元网格划分采用边长为1 m的矩形单元。

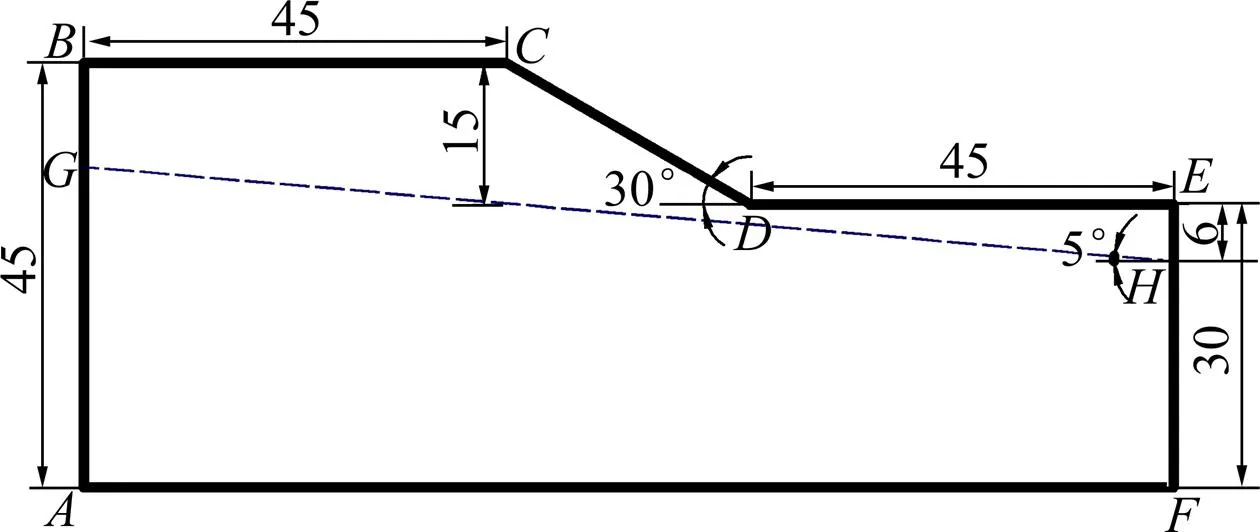
数据单位：m

3.2 计算参数

数值分析过程中控制降雨条件不变，根据文献[10]中的降雨量，本次分析中取降雨强度为22 mm/h(即6.1 μm/s)，降雨持时24 h。在分析过程中先控制土体强度参数不变，研究土体渗透系数对迟滞现象的影响。再控制土体渗透参数，研究土体强度参数与迟滞现象的关联性。

3.2.1 土体渗透性对迟滞现象的影响分析

根据文献[10，20−21]选取3组基本土质参数，分别命名为土质1组、土质2组、土质3组，其参数取值情况见表1。3组土质的土水特性曲线如图4所示。分别以这3组参数取值为基础，以等步长递增变换每组土质的饱和渗透系数取值，研究不同土体渗透系数与降雨触发边坡失稳迟滞现象的关联性，各组饱和渗透系数的取值见表2。

表1 3组土质基本参数取值

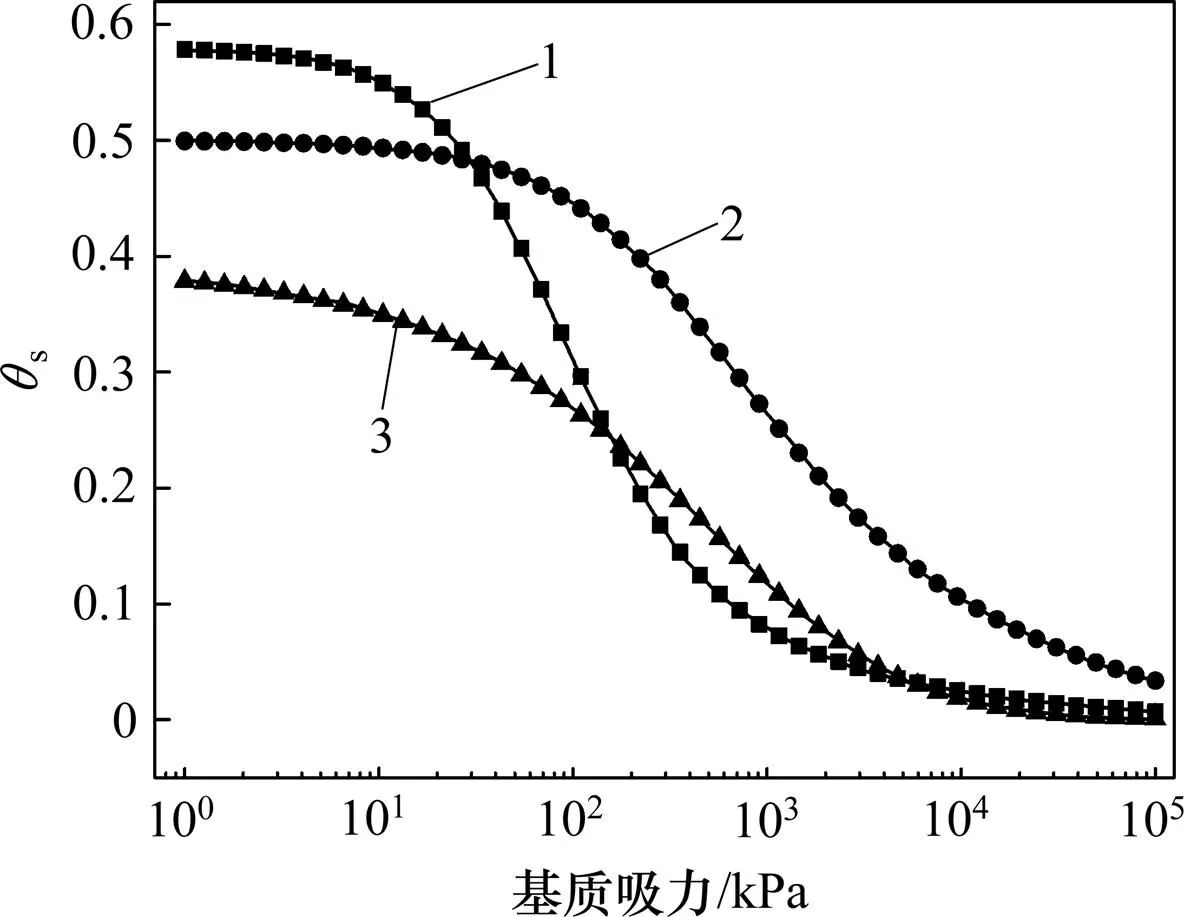
1—土质1组；2—土质2组；3—土质3组。

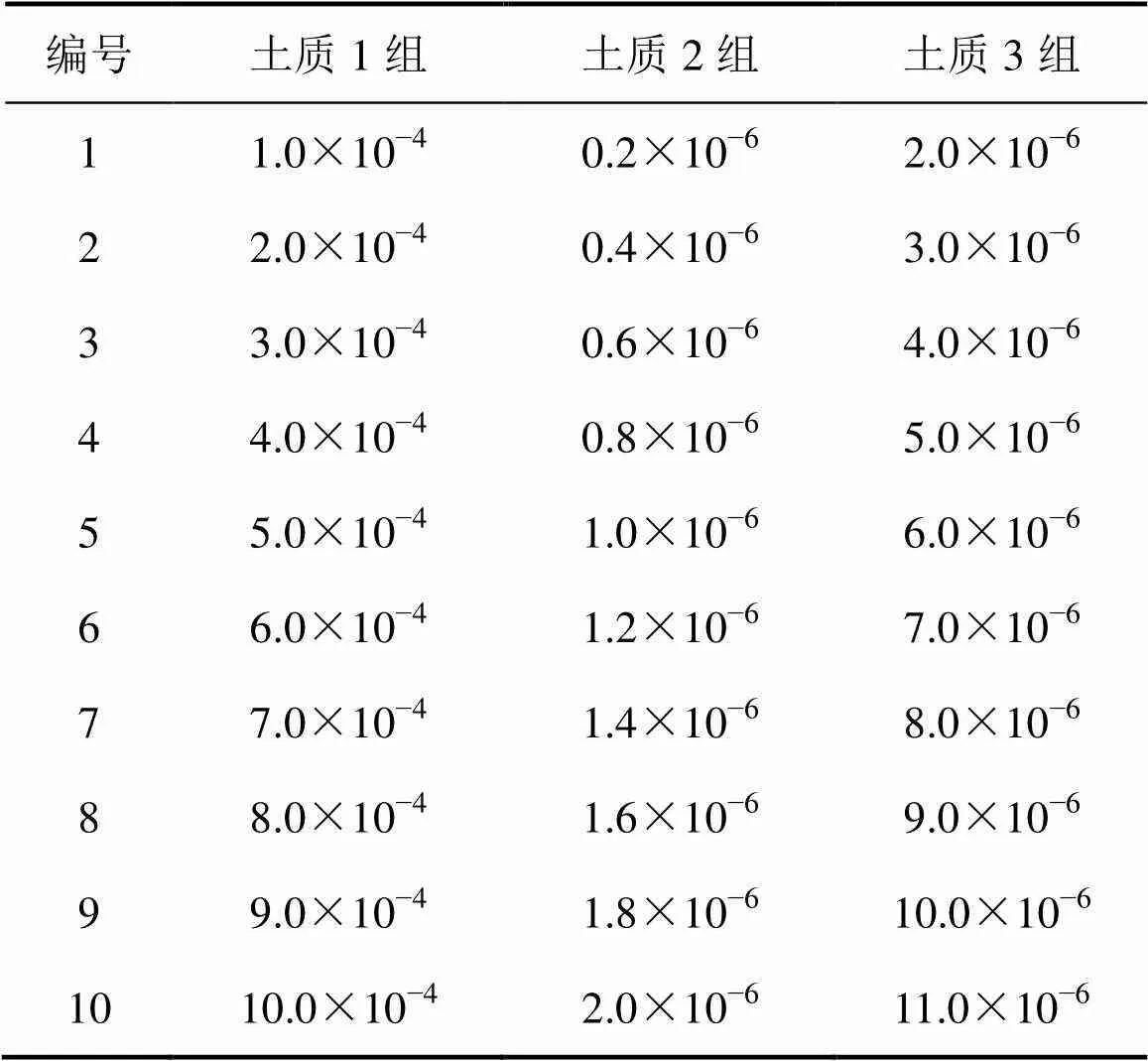
表2 3组土质饱和渗透系数ks

3.2.2 土体强度参数对迟滞现象的影响

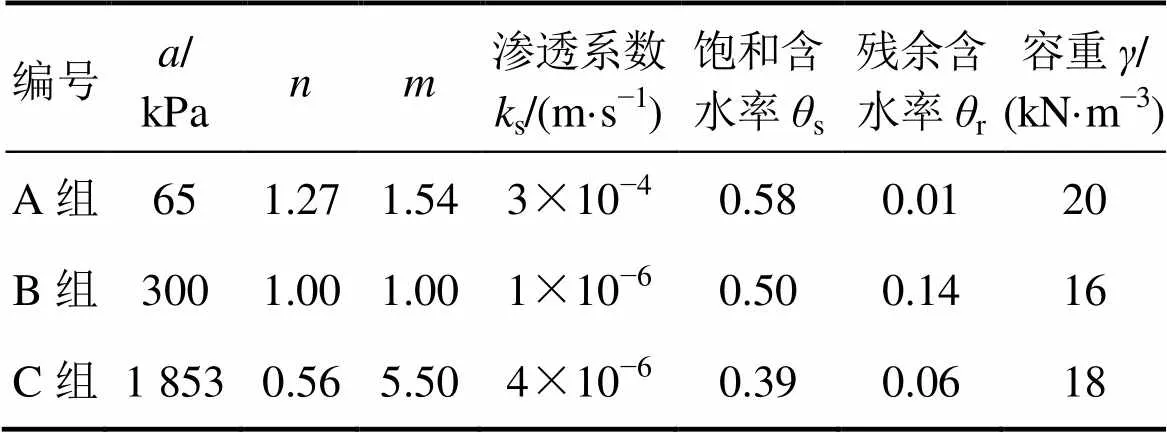
表3 3组土质基本参数取值

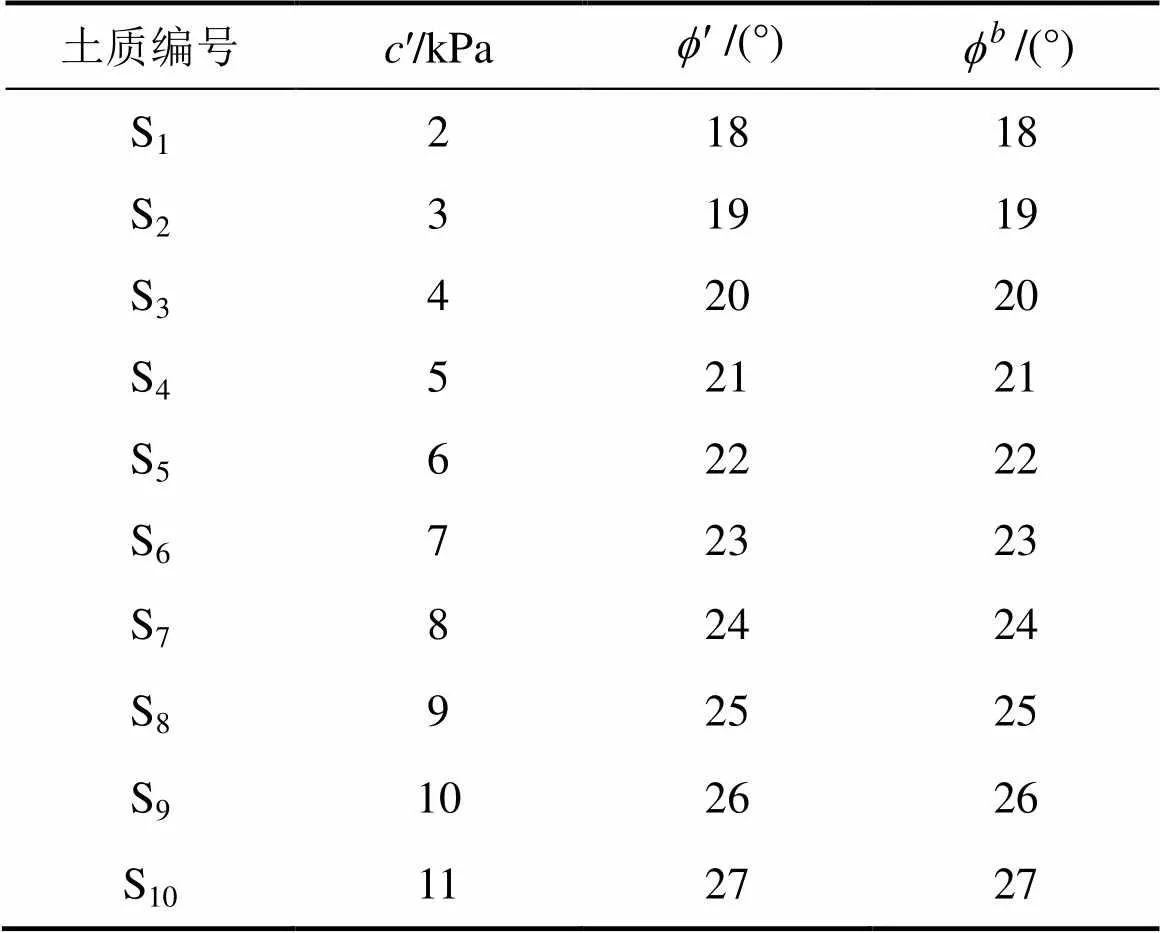
表4 土体强度参数取值

1—A组；2—B组；3—C组。

3.3 临界时间定义

临界时间定义如下：在降雨条件下，因雨水入渗导致坡体稳定性发生变化，这种变化体现在坡体安全系数在降雨过程中及降雨结束后的波动性上。因雨水作用导致的坡体稳定性变化有3种不同情况(如图6所示，以降雨开始时间为计时零点，0表示降雨结束时间)：曲线1表征降雨过程中坡体失稳，失稳时间点记为a；曲线2表征降雨结束一段时间后坡体失稳，即出现迟滞现象，失稳时间点记为b；曲线3表征降雨过程中坡体没有失稳，但因雨水作用出现了安全系数曲线的最小值，记最小安全系数取得时间点为c(点也可能出现在降雨结束之前)。在本次分析中，将a，b和c统一定义为临界时间。临界时间包含2层含义：既表征坡体的最不稳定时间，又表征从降雨开始到坡体最不稳定状态(包含安全系数为1的临界状态)所需要的时间。

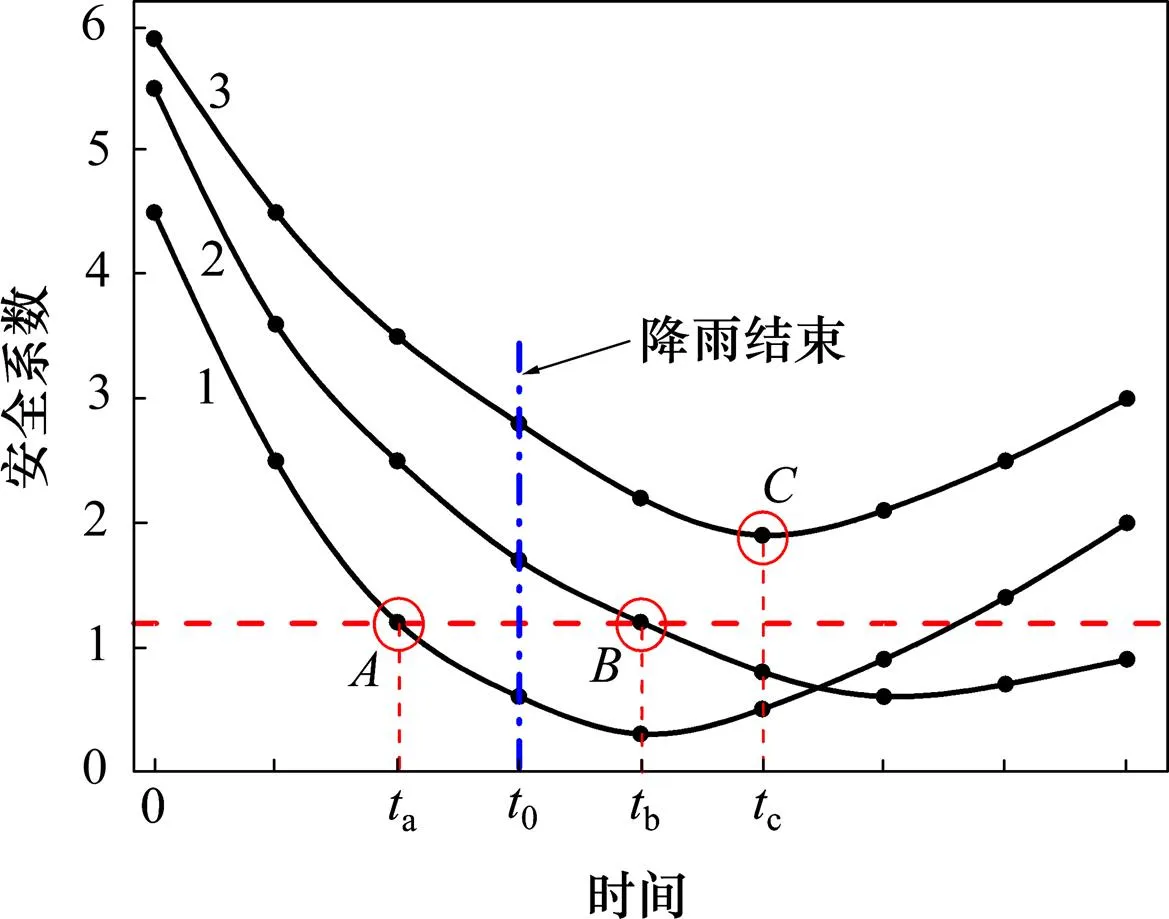
图6 临界时间定义

4 计算结果及分析

4.1 渗透性影响分析

土体渗透性对临界时间的影响如图7所示。从图7可见：在3类土质下，临界时间随渗透系数增大具有相似的变化趋势，即随渗透系数增大，临界时间逐渐变小；在图7(a)所示情况下，临界时间均在24 h以内，说明在降雨过程中坡体失稳，渗透性越好，发生失稳的时间越短；在图7(b)所示情况下，当饱和渗透系数小于1.2 μm/s时，临界时间均大于24 h，即坡体临界状态会在降雨结束后出现，其中A和B情形下均出现了明显的滑坡滞后失稳现象；当饱和渗透系数大于1.2 μm/s时，随饱和渗透系数的增大，临界时间逐渐变小，但变化趋势趋于平缓；对于图7(c)所示情况，随渗透系数增大，临界时间变化趋于平缓并接近24 h，说明该情形下坡体的最不稳定状态均趋于在降雨结束之后出现。综合比较这3种情形，土质2组与土质3组较容易产生滑坡失稳滞后情形，而土质1组则倾向于在降雨过程中发生滑坡，其主要是：1) 土质1组的饱和渗透系数(数量级为10−4 m/s)较土质2组与3组的饱和渗透系数(数量级为10−3m/s)高；2) 土水特性曲线(见图4)显示土质1组进气值点较低且进气值较小[22](主要体现在，和的取值上)，即对于土质1组土体而言易于进气排水。

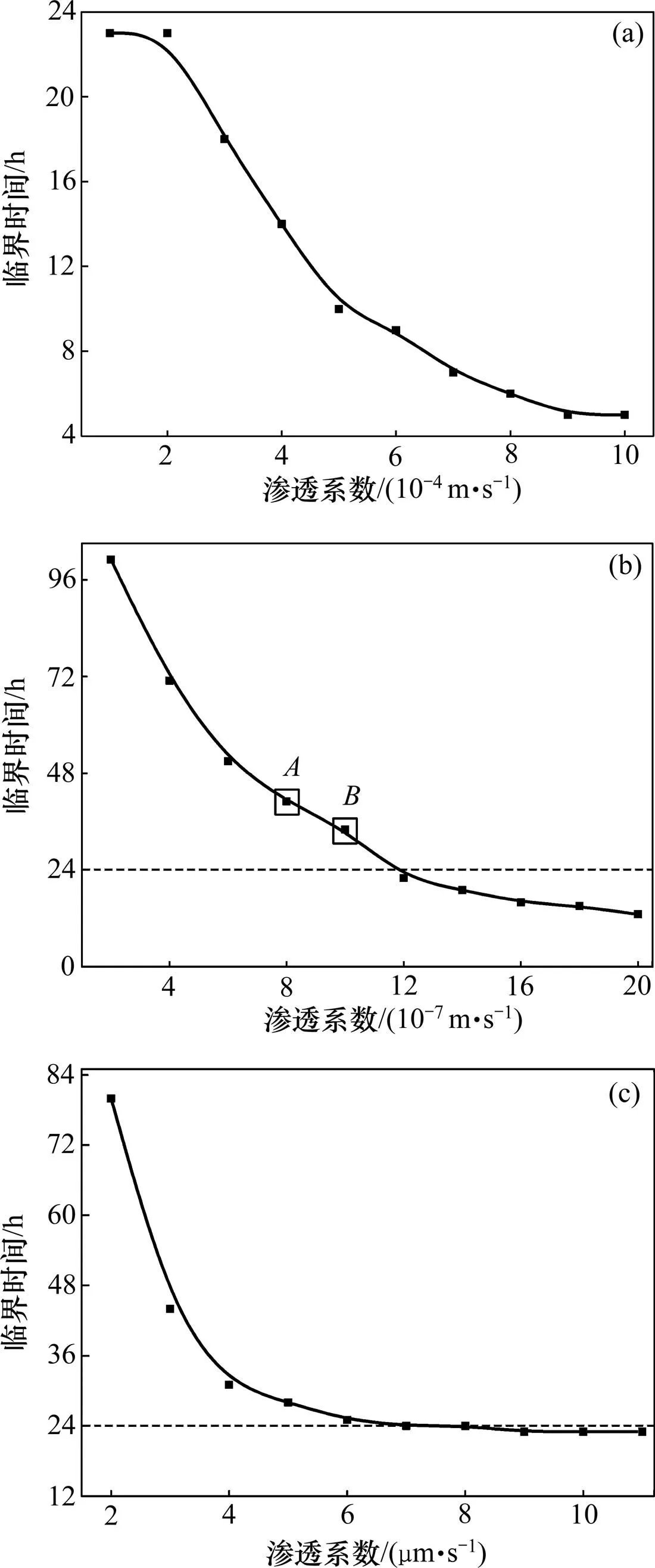
(a) 土质1组；(b) 土质2组；(c) 土质3组

4.2 土体强度影响分析

土体强度对临界时间的影响如图8所示。从图8可见：3组土质坡体的临界时间均随土体强度参数增大而呈现出不断增大并最终趋于平缓的变化趋势；A组土坡的临界时间均小于24 h，说明在该情形下，不论土体强度如何取值，边坡基本会在降雨过程中失稳，进一步表明土体渗透特性对降雨触发滑坡的发生时间具有决定性影响；B组土坡的临界时间对土质强度的变化较敏感，当土体强度较低时，坡体会在降雨过程中失稳；当土体强度进一步增大时，迟滞现象越来越明显，并最终趋于稳定。这说明土体强度对迟滞现象的发生有影响，在土体强度较小时坡体在降雨过程中失稳。C组土坡的临界时间对土质强度增加的变化趋势与B组的类似，只是较B组较平缓，说明土体强度对迟滞现象的影响受土体渗透特性的制约。

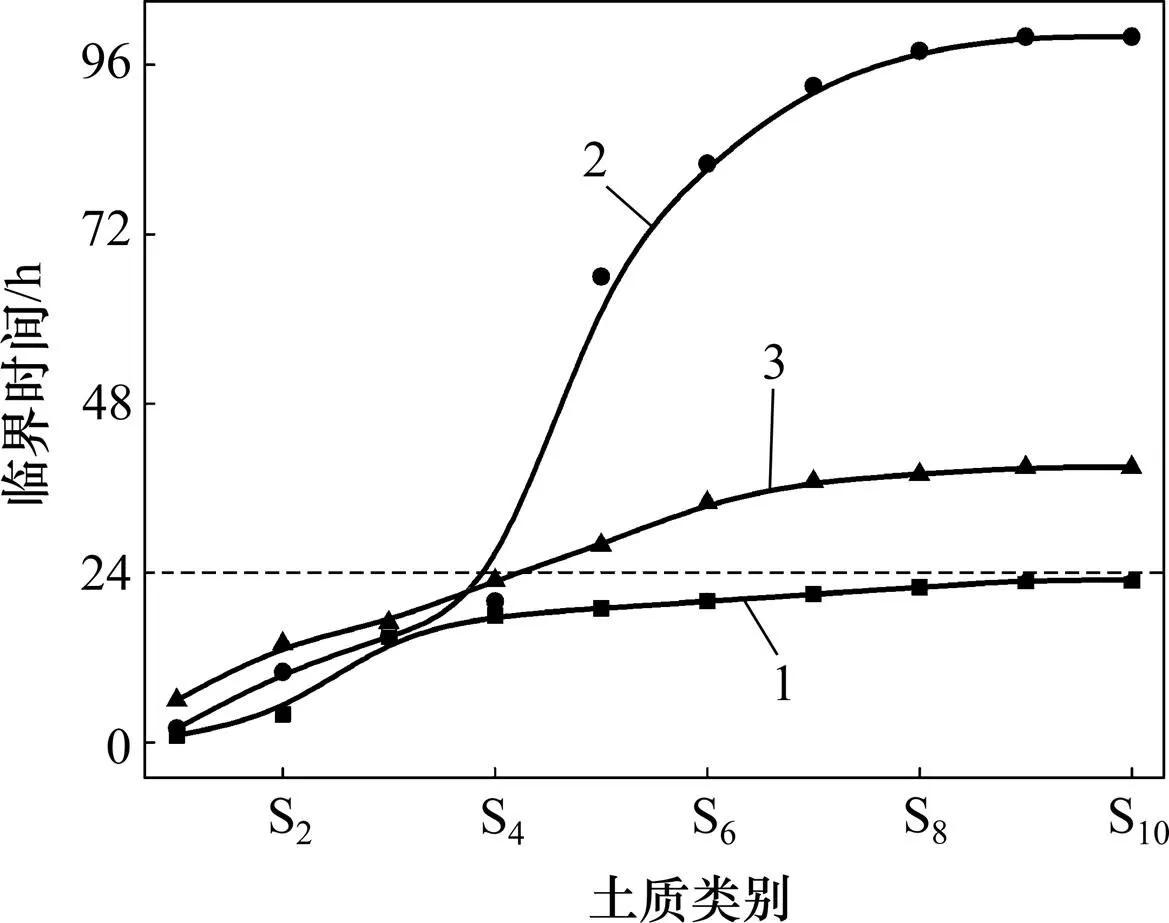
1—A组；2—B组；3—C组。

5 结论

1) 随土体渗透能力增强，坡体的临界时间呈现出不断减小并最终趋于平缓的变化趋势。在特定的土体强度下，渗透性较好(渗透系数s大于1×10−4 m/s)且进气排水能力较强的土质坡体倾向于在降雨过程中失稳。当渗透系数s在1×10−6~1×10−7 m/s范围内取值时，坡体的临界时间通常在降雨结束后取得。

2) 当土体渗透性一定时，随着土体强度增大，坡体的临界时间呈现出不断增大并最终趋于平缓的变化趋势。

3) 土体渗透性对迟滞现象的产生有主导作用，即渗透性较好的土坡倾向于在降雨过程中失稳，此时土体强度对该过程的影响较小。当土体渗透性适宜、坡体可能产生失稳迟滞现象时，土体强度对迟滞现象产生影响，且在土体强度较低时起主导作用，此时坡体倾向于在降雨过程中失稳。

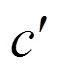
[1] CHANDRASEKARAN S S, OWAISE R S, ASHWIN S. Investigation on infrastructural damages by rainfall induced landslides during November 2009 in Nilgiris, India[J]. Nat Hazards, 2013, 65(3): 1535−1557.

[2] 田东方, 郑宏, 刘德富. 考虑径流影响的滑坡降雨入渗二维有限元模拟及应用[J]. 岩土力学, 2016, 37(4): 1179−1186. TIAN Dongfang, ZHENG Hong, LIU Defu. 2D FEM numerical simulation of rainfall infiltration for landslide with considering runoff effect and its application[J]. Rock and Soil Mechanics, 2016, 37(4): 1179−1186.

[3] 张群, 许强, 易靖松, 等. 南江红层地区缓倾角浅层土质滑坡降雨入渗深度与成因机理研究[J]. 岩土工程学报, 2016, 38(8): 1447−1455. ZHANG Qun, XU Qiang, YI Jingsong, et al. Rainfall infiltration depth and formation mechanison of low-inclination soil landslides in Nanjiang[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(8): 1447−1455.

[4] RAHARDJO H, LEE T T, LEONG E C, et al. A flume for assessing flux boundary characteristics in rainfall-induced slope failure studies[J]. Geotechnical Testing Journal, 2004, 27(2): 145−153.

[5] WU L Z, HUANG R Q, XU Q, et al. Analysis of physical testing of rainfall-induced soil slope failures[J]. Environ Earth Sci, 2015, 73(12): 8519−8531.

[6] SEBOONG O, LU N. Slope stability analysis under unsaturated conditions: case studies of rainfall induced failure of cut slopes[J]. Engineering Geology, 2015, 184: 96−103.

[7] TANG M G, XU Q G, HUANG R Q. Site monitoring of suction and temporary pore water pressure in an ancient landslide in the Three Gorges reservoir area, China[J]. Environ Earth Sci, 2015, 73(9): 5601−5609.

[8] XU Q J, ZHANG L M. The mechanism of a railway rainfall effect on slope[J]. Landslides, 2015, 7(2): 149−156.

[9] TU X B, KWONG A K L, DAI F C, et al. Field monitoring of rainfall infiltration in a loess slope and analysis of failure mechanism of rainfall-induced landslides[J]. Engineering Geology, 2009, 105(1): 134−150.

[10] RAHARDJO H, NIO A S, LEONG E C, et al. Effects of groundwater table position and soil properties on stability of slope during rainfall[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(11): 1555−1564.

[11] DOU H Q, HAN T C, GONG X N, et al. Probabilistic slope stability analysis considering the variability of hydraulic conductivity under rainfall infiltration redistribution conditions[J]. Engineering Geology, 2014, 183: 1−13.

[12] DOU H Q, HAN T C, GONG X N, et al. Effects of the spatial variability of permeability on rainfall induced landslides[J]. Engineering Geology, 2015, 192: 92−100.

[13] TAKE W A, BEDDOE R A. Base liquefaction: a mechanism for shear-induced failure of loose granular slopes[J]. Can Geotech J, 2014, 51(5): 496−507.

[14] TAKE W A, BEDDOE R A, ROYA D B, et al. Effect of antecedent groundwater conditions on the triggering of static liquefaction landslides[J]. Landslides, 2015, 12(3): 469−479.

[15] FREDLUND D G, MORGENSTERN N R. Constitutive relations for volume change in unsaturated soils[J]. Canadian Geotechnical Journal, 2011, 13(3): 261−276.

[16] FREDLUND D G, MORGENSTERN N R. Stress state variables for unsaturated soils[J]. ASCE, 1977, 103(5): 447−464.

[17] FREDLUND D G, XING Anqing. Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(4): 521−532.

[18] VAN GENUCHTEN, TH M. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(44): 892−898.

[19] RAHIMI A, RAHARDJO H, LEONG E C, et al. Effect of antecedent rainfall patterns on rainfall-induced slope failure[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(5): 483−491.

[20] 曹平, 张科, 汪亦显, 等. 多层边坡破坏机制数值模拟研究[J]. 岩土力学, 2011, 32(3): 872−878.CAO Ping, ZHANG Ke, WANG Yixian, et al. Numerical simulation of failure mechanism of multilayer slope[J]. Rock and Soil Mechanics, 2011, 32(3): 872−878.

[21] RAHIMI A, RAHARDJO H, LEONG E C, et al. Effect of antecedent rainfall patterns on rainfall-induced slope failure[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 137(5): 483−491.

[22] 李广信. 高等土力学[M]. 北京: 清华大学出版社, 2004: 193−194.LI Guangxin. Advanced soil mechanics[M]. Beijing: Tsinghua University Press, 2004: 193−194.

(编辑 陈灿华)

Delay phenomenon of shallow slope failure triggered by rainfall and its correlation with soil parameters

ZHANG Jian, LI Jiangteng, LIN Hang, HUANG Minpeng, CHANG Ruiqin

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

The effect of rainfall on the slope may continue and the most unstable state may occur after rainfall stops. This phenomenon was described as the delay phenomenon. According to the infiltration characteristics of rainwater in the soil, two representative models of landslides occurring after rainfall were set up to illustrate the mechanisms of the delay phenomenon. The concept of critical moment was defined. The relationship between the delay phenomenon and soil parameters was analyzed using numerical analysis method. The results show that the delay phenomenon has a direct relationship with soil permeability parameters and soil strength parameters. The soil slope tends to have failure during rainfall when the permeability coefficient is larger than 1×10 −4m/s and air intake and discharge capacity are strong. The slope tends to be in the most unstable state when the permeability coefficient is between 1×10−7m/s to 1×10−6m/s. When the soil strength parameters are determined, the critical moment of the slope decreases firstly and eventually becomes stable with the increase of the permeability coefficient. The critical moment of the slope increases firstly and tends to be stable with the increase of the soil strength parameters when the permeability coefficient is determined. Soil permeability is the major influencing factor of the delay phenomenon. When permeability is fitted, soil strength parameters have dominant efficient when the soil strength is low.

slope; rainfall; delay phenomenon; soil permeability; soil strength

TU443

A

1672−7207(2018)01−0150−08

10.11817/j.issn.1672-7207.2018.01.020

2017−03−10；

2017−05−21

长江科学院开放基金资助项目(CKWV2016390/KY)；湖南省研究生科研创新项目(CX2017B055)；长沙理工大学道路灾变防治及交通安全教育部工程研究中心开放基金资助项目(KFJ160403) (Project(CKWV2016390/KY) supported by the CRSRI Open Research Program; Project(CX2017B055) supported by Hunan Provincial Innovation Foundation for Postgraduate; Project(KFJ160403) supported by Open Fund of Engineering Research Center of Catastrophic Prophylaxis and Treatment of Rood & Traffic Safety of Ministry of Education (Changsha University of Science & Technology))

李江腾，博士，教授，从事岩土工程材料及岩土工程灾害研究；E-mail: ljtcsu@163.com