亚微米级运动平台结构优化及实现

徐聪，段吉安，唐皓，李帅

亚微米级运动平台结构优化及实现

徐聪1，段吉安1，唐皓1，李帅2

(1. 中南大学高性能复杂制造国家重点实验室，湖南长沙，410083；2. 中南大学信息工程学院，湖南长沙，410083)

为实现一种直流电机驱动的亚微米级运动平台的设计，并尽量减小其运动误差，采用Simulink−M文件混合仿真的方法，结合Stribeck摩擦模型，探讨运动平台丝杠、同步带的相关结构、精度参数对运动平台精度的影响。通过分析并针对实际使用的要求，进行平台最优结构设计。使用EMAC200控制器和XL-80激光干涉系统对运动平台进行实际测试。研究结果表明：运动平台误差主要受丝杠导程、同步带传动比及它们精度的影响；随着导程减小，传动比增大，精度提高，稳态误差呈减小趋势；当行程为1 mm时，稳态误差在±1.5 μm之内，并且可以达到50 nm的实际分辨率；通过Simulink−M文件混合仿真方法，可以实现精密运动平台这种复杂非线性系统的结构优化，提高系统实际的定位精度。

精密运动平台；Simulink−M混合仿真；结构优化；误差

随着超精密加工、半导体、微纳制造、光电子通讯技术的飞速发展，人们对精密运动平台的精度要求越来越高[1−3]。特别是随着新型大容量、多通道光电子器件的出现，人们对光电子耦合精度要求越来越高[4]。光电子器件耦合精度主要由搭载其运动的光学运动平台决定，作为光电子封装领域基础部件，提高运动平台运动精度是提高光电子耦合效率的基础。为获得更高的定位精度和分辨率，近年来精密运动平台出现了诸多新型的结构。直线电机、压电陶瓷、音圈电机等驱动方式结合柔性铰链、气浮导轨等导向机构将精密运动推向了一个新的阶段[5−8]。虽然这些新型结构具有分辨率高、零间隙、摩擦小等特点，但由于滚珠丝杆、滚动导轨结构简单、系统刚性好，对控制器要求较低，容易实现鲁棒控制，并且技术成熟、成本低廉，通过适当改进可以实现大部分极限定位[9−10]，因此，滚珠丝杠、滚动导轨在精密运动平台的使用中依然占据主导地位。为此，本文作者采用同步带、滚珠丝杠、交叉滚珠导轨结构，设计一款基于直流电机驱动的运动平台，以期实现亚微米级运动。精密运动平台主要技术难点在于如何减少误差。运动平台几何误差可以采用多体系统理论进行分析，用特征矩阵表示多体系统中个体间的相对位置及姿态，从而完成误差传递分 析[11−12]。但由于存在摩擦、反馈噪声、传动间隙等非线性因素[13]，运动平台还存在随机动态误差，它不仅与传动链上的各个零件精度有关，而且与各个零件的质量、刚性以及尺寸等有关。若将运动平台的动态误差与其结构参数结合，探讨它们之间的关系，则可以完成以误差最小为目标的运动平台结构的优化设计。本文作者采用Simulink−M文件混合仿真方法，对运动平台的动态误差与其结构参数之间的关系进行分析，从而实现运动平台结构优化。Simulink是MATLAB中框图式的仿真环境，可以快捷地建立系统的传递函数；M文件通过代码执行，可以快速实现循环和数据处理。混合仿真过程首先在Simulink中建立系统模型，并通过M文件中相关函数设置Simulink的相关参量，然后返回Simulink仿真得到稳态误差，并对不同结构参量所得到的误差进行分析，从而得到它们与运动平台误差之间的关系，达到运动平台结构优化的目的[4]。

1 基于DC驱动的亚微米级运动平台建模

1.1 平台结构

本文设计的平台采用直流电机驱动、同步带、滚珠丝杠传动、交叉滚珠导轨导向结构。丝杠和同步带传动结构具有较大的传动比，结合高分辨率的TONIC光栅尺以及直流测速机，使运动平台具有很高分辨率。采用直流电机驱动，运动平台不仅响应快，而且具有更好的低速稳定性、更小的震动。交叉滚珠导轨代替传统的直线导轨，由于减少了滚珠循环环节，因此，阻尼更小，导向精度和刚性更高。整体采用内嵌式布局，运动平台结构更加紧凑，有利于提高多维系统的整体精度。

1.2 运动平台控制方式

运动平台包含位置、速度、电流三环反馈，见图1。系统位置反馈采用5 nm分辨率的光栅尺；速度环反馈使用高分辨率的直流测速机，电流环则直接集成在电机驱动器内，由驱动器自行调整；使用EMAC200作为系统控制器，内置PID算法通过PWM对电机进行调速控制，从而完成运动平台的运动控制。

图1 运动平台控制和传动示意图

1.3 机电耦合数学模型

对于所研究的运动平台驱动机构，电机可以简化成电阻、电感组成的等效电路。同步带则可以简化成2个具有一定转动惯量、阻尼并通过弹簧连接的轮传动系统。滚珠丝杠的转子与螺母之间的连接可以等效为具有一定斜度的两锲块间的弹性阻尼环节，见图2。

图2 运动平台等效模型

图2中：d为电动机电枢电感；d为电枢电阻；d为电枢电流；为电动机输入电压；1为电动机转角；2为大同步带转角；1和2分别为小、大皮带轮直径；1为小带轮及电机转子转动惯量之和；2为大带轮转动惯量；3为丝杠的转动惯量；b为皮带的劲度系数；sd为丝杠的转动阻尼系数；为平台的质量；0为运动平台的摩擦力；s丝杠与螺母间的刚度；为平台位移；s为丝杠螺母螺杆间的阻尼系数。

1.3.1 直流电机数学模型

直流电机通过改变电枢电压进行转速调节。根据电动机回路电压方程、转速和电流方程以及系统动力学方程[14]，可得到直流电机的机电耦合方程，然后对其进行拉氏变换，得到直流电机旋转角度与电枢电压的传递函数为

式中：m为转矩常数；R为电机轴上的等效转动惯量；R为电机轴上等效阻尼。

1.3.2 同步带传动数学模型

同步带建模首先将同步带转动惯量等效到电机轴上，将其假设为2个具有一定预紧力的弹簧，并进行无质量化处理。根据简化的皮带模型可得到系统动力学模型，然后对其进行拉氏变换，可得皮带轮输出角度和输入角度的传递函数为

1.3.3 滚珠丝杠传动数学模型建立

式中：­f为滚珠丝杠的输入力矩。

2 基于Simulink−M混合仿真过程

2.1 Simulink−M混合仿真介绍

Simulink是Matlab中框图式仿真模块，具有结构清晰、建模迅速等优点，但实现循环和寻优等操作复杂，执行效率低。M文件编程环境代码执行，对数据处理较方便，但程序结构复杂，对复杂模型建模较困难[16]。将这两者结合起来，首先通过M文件set_param( )函数设置Simulink模型中的参数、sim( )函数运行Simulink函数仿真，并运用Simulink中OUT输出模块将稳态误差输出到workspace中，运用M文件中meshgrid( )函数生成网格采样点、surf( )函数进行绘图，完成稳态误差与结构参数的关系分析，达到优化系统结构的目的。基于Simulink−M混合仿真示意图见图3。

图3 基于Simulink−M混合仿真示意图

2.2 STRIBECK摩擦模型

当克服静摩擦力之后，在低速下摩擦力随着速度的增加而减小[17]，如图4(a)所示。该模型很好地描述了低速、微动摩擦行为。由于Stribeck效应的存在，摩擦力将产生不稳定效应，能够较好地模拟运动平台微行程时的摩擦情况。

在Simulink中，设计了1个基于Stribeck摩擦模型的反馈模块，通过仿真分析得到的摩擦曲线可以很大程度地模拟Stribeck摩擦曲线，如图4(b)所示。

2.3 丝杠摆动误差和同步带传动误差模型

丝杆与同步带属于旋转零件，导程和传动比误均具有一定周期性，其中丝杆的导程误差由累计误差和在丝杆旋转周内周期性变化的摆动误差组成，见图5；同步带传动比误差与同步带轮节距误差相关，也是1个周期性误差。

(a) Stribeck摩擦模型；(b) Simulink仿真曲线

在Simulink内，使用1个常数模块和正弦模块之和模拟实际的丝杆导程、同步带传动比的误差。

图5 丝杠导程误差

2.4 系统Simulink模型

图6所示为系统的闭环Simulink框图，包含PID控制、式(1)所得到的直流电机传递函数(电机参数由使用条件已经确定)、式(2)所得到同步带传递函数、式(5)所得到丝杆传递函数，结合误差干扰、Stribeck摩擦模型等，采用Step模块模拟系统输入，Backlash模块模拟丝杆、同步带反向间隙。其中，相关系统结构参数如丝杠导程、直径、精度a、同步带传动比倒数、同步带宽度、同步带精度a，其值通过M文件设置(模型中忽略了极小项参数)。图7所示为Simulink单次阶跃仿真结果，其中，s为稳态误差，通过M文件计算稳定时间内(100~200 ms)最大位移与最小位移之差而得(在实际过程中，只通过M文件计算s，不进行阶跃响应绘图)。

联合仿真过程，首先通过M文件设置相关参数(丝杠导程、直径、精度a、同步带传动比倒数、同步带宽度、同步带精度a)，然后将每次仿真生成的误差通过Simulink中的out模块输出到workspace中，最后通过M文件分析数据。仿真初始设定PID参数和Stribeck模块中相关摩擦参数。在仿真过程中，丝杠导程从1~5 min，直径从4~8 mm，丝杠精度a从0.001~0.01 mm，同步带传动比倒数从0.2~1.0，同步带宽度从1~10 mm，同步带精度a从0.002~0.010 mm进行线性变化。

图6 系统Simulink框图

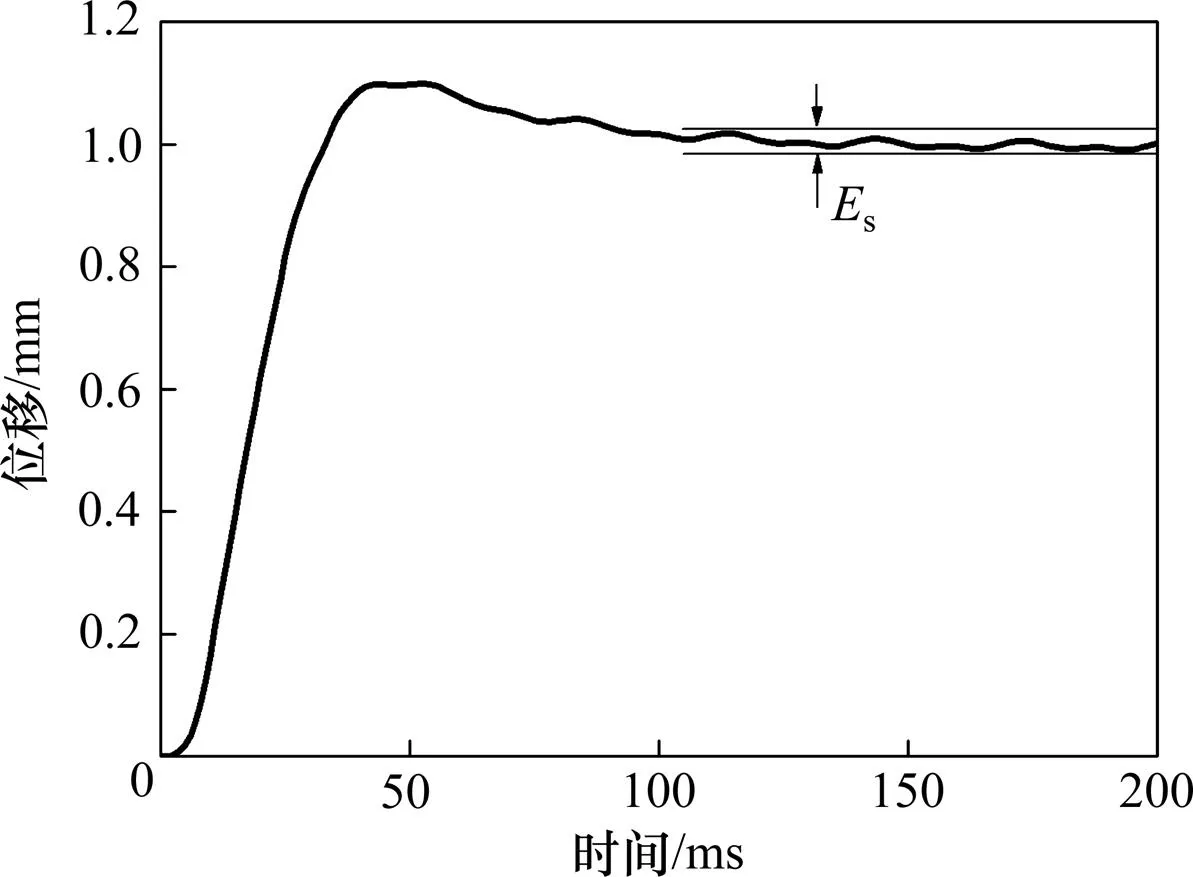
图7 运动平台时域响应曲线

3 仿真结果分析

3.1 稳态误差与传动链参数的关系

通过Simulink−M文件的混合仿真，经过多次循环后分别得到运动平台1 mm响应下的误差s与丝杆导程、同步带传动比倒数、丝杆精度a、同步带精度a、丝杆直径、同步带宽度的关系，见图8。

通过仿真发现：当同步带传动比倒数在0.8以上、丝杆导程在3 mm以上时，系统稳态误差s基本保持不变；而当丝杠导程从3 mm、传动比倒数从0.8不断减小时，稳态误差s呈现急剧减小趋势(图8(a))。

在传动精度影响方面，随着同步带精度a、丝杠精度a不断提高，稳态误差s不断减小，但稳态误差s在丝杠、同步带为某些特定组合时有突变，在设计时应避免这些区域(图8(b))。

通过研究丝杠直径、同步带宽度时发现：2个结构对稳态误差s影响趋势一致，均是随着结构的增大，稳态误差s先增加后减小，在中间处达到极值。从稳态误差a的变化可以发现这2个结构变化引起的误差变化非常小(图8(c))。

(a) 稳态误差Es与丝杠导程L同步带传动比倒数R的关系；(b) 稳态误差Es与同步带传动精度Ra、丝杠精度La的关系；(c) 稳态误差Es与丝杠直径D、同步带宽度B的关系

3.2 运动平台误差敏感性分析

传动链误差敏感性是分析传动链误差来源的重要依据。优化敏感性较高的零件，可以减小系统的整体误差。选择合适的结构参数作为基值，以一定的误差变化量考察，从而得到结构参数的变化。定义参数为误差敏感性因子，即基值与结构参数的变化量的比值。通过分析仿真，以2 mm，0.5，0.003 μm，0.005 μm，5 mm和6 mm分别作为丝杆导程、同步带传动比倒数、丝杆精度a、同步带精度a、同步带宽度、丝杠直径的基值，以系统1 μm误差作为变化，得到基值与各结构参数变化量的比例，见图9。从图9可见：同步带、丝杆的精度对系统整体影响最大，其次是它们的传动比及导程，而丝杆直径、同步带宽度对误差影响最小。因此，采用较大的同步带传动比、较小的丝杆导程并提高它们的传动精度可以有效地减小运动平台系统的整体误差。

图9 误差敏感性因子

4 实验测试

通过仿真分析，并结合结构设计要求，最终选择导程为1 mm、直径为8 mm、精度等级为C3的滚珠丝杆，传动比为2、宽度为5 mm的高精度同步带作为运动平台传动部件的最优结构，并选择EMAC200控制器作为运动平台控制器，完成运动平台的样机研制，见图10。

图10 运动平台测试图

实验测试使用雷尼绍XL-80激光干涉系统。系统由XL-80激光头、反射分光镜组、XC-80温度补偿器组成，通过PC机处理测试，测试结果如图11所示。从图11可见：当行程为1 mm时，定位误差在±1.5 μm以内(图11(a))；在进行50 nm最小行程运动时，定位误差稳定在±10 nm以内(图11(b))，满足实际需要。通过对运动平台进行1.0 μm和0.1 μm阶梯定位测试后发现，运动平台在微小行程运动时具备较好的定位性能，运动平台实现了亚微米级运动的能力(图11(c)和图11(d))。

(a) 1 mm位移测试结果；(b) 50 nm位移测试结果；(c) 1 μm阶梯定位测试结果；(d) 0.1 μm阶梯定位测试结果

实验测试结果表明：通过优化运动平台的结构，基于DC驱动的光学精密运动平台可以达到50 nm的运动分辨率；系统超调量明显偏大，不利于实际应用，后期将结合轨迹规划、模糊PID控制策略等方式实现无超调系统设计。

5 结论

1) 基于Simulink−M文件混合仿真的方法，可以方便地得到基于直流电机驱动的运动平台误差与传动环节的零件误差、传动比、结构的关系，从而实现这种复杂非线性系统的优化设计。

2) 同步带、丝杆的精度对系统整体影响最大，其次是传动比及导程，而丝杆直径、同步带宽度对误差影响最小。采用较大的同步带传动比、较小的丝杆导程并提高它们的传动精度可以有效地减小运动平台运动误差。

3) 使用滚珠丝杠、同步带驱动方式，结合高分辨率光栅尺、高响应直流电机可以实现亚微米光学运动平台的设计，而采用Simulink−M文件混合仿真的方法可以实现基于误差最小为目标的优化设计。

[1] 陈兴林, 刘川, 耿长青, 等. 光刻机工件台直线电机的完全跟踪控制[J]. 中南大学学报(自然科学版), 2015, 46(9): 3238−3244. CHEN Xinglin, LIU Chuan, GENG Changqing, et al. Perfect tracking control for linear motor in wafer stage of lithography[J]. Journal of Central South University (Science and Technology), 2015, 46(9): 3238−3244.

[2] TEO T J, CHEN I M, YANG G. A large deflection and high payload flexure-based parallel manipulator for UV nanoimprint lithography. Part I: modeling and analyses[J]. Precision Engineering, 2014, 38(4): 861−871.

[3] 阳波, 段吉安. 光电子封装超精密运动平台末端姿态调整[J]. 中南大学学报(自然科学版), 2011, 42(5): 1290−1295. YANG Bo, DUAN Jian. Opto-electronics packaging platform for ra-precision position and attitude adjustment[J]. Journal of Central South University (Science and Technology), 2011, 42(5): 1290−1295.

[4] 王兴军, 苏昭棠, 周治平. 硅基光电子学的最新进展[J]. 中国科学: 物理学力学天文学, 2015, 45(1): 014201. WANG Xingjun, SU Zhaotang, ZHOU Zhiping. Recent progress of silicon photonics[J]. Scientia Sinica (Physica, Mechanica & Astronomica), 2015, 45(1): 014201.

[5] 张刚, 刘品宽, 张波, 等. 直线电机精密运动平台轨迹跟踪控制器设计[J]. 光学精密工程, 2013, 21(2): 371−379. ZHANG Gang, LIU Pinkuang, ZHANG Bo, et al. Design of trajectory tracking controller for precision position table driven by linear motor[J]. Optics and Precision Engineering, 2013, 21(2): 371−379.

[6] CHU C L, FAN S H. A novel long-travel piezoelectric-driven linear nanopositioning stage[J]. Precision Engineering, 2006, 30(1): 85−95.

[7] CHEN Qiming, LI Liyi, WANG Mingyi, et al. The precise modeling and active disturbance rejection control of voice coil motor in high precision motion control system[J]. Applied Mathematical Modelling, 2015, 39(19): 5936−5948.

[8] ZHANG Deyuang, LÜ Jianlu, JIANG Y, et al. A piezoelectric microvalve with a flexure-hinged driving frame and micro fabricated silicon sealing pair[J]. Mechatronics, 2014, 24(5): 511−518.

[9] FUKADA S, FANG B, SHIGENO A. Experimental analysis and simulation of nonlinear microscopic behavior of ball screw mechanism for ultra-precision positioning[J]. Precision Engineering, 2011, 35(4): 650−668.

[10] PAWEŁKO P, BERCZYŃSKI S, GRZĄDZIEL Z. Modeling roller guides of preload[J]. Archives of Civil and Mechanical Engineering, 2014, 14(4): 691−699.

[11] TIAN Wenjie, GAO Weiguo, ZHANG Dawei, et al. A general approach for error modeling of machine tools[J]. International Journal of Machine Tools & Manufacture, 2014, 79(4): 17−23.

[12] SRIVASTAVA A K, VELDHUIS S C, ELBESTAWIT M A. Modeling geometric and thermal errors in a five-axis cnc machine tool[J].International Journal of Machine Tools and Manufacture, 1995, 35(9):1321-1337.

[13] FUTAMI S, FURUTANI A, YOSHIDA S. Nanometer positioning and its micro-dynamics[J]. Nanotechnology, 1998, 1(1): 31−37.

[14] ZEINA B, SAMIH A J, IMAD K. Modeling and simulation of series DC Motors in electric car[J]. Energy Procedia, 2014, 50: 460−470.

[15] MAEDA G J, SATO K. Practical control method for ultra-precision positioning using a ball screw mechanism[J]. Precise Engineering, 2008, 32(4): 309−318.

[16] 王玥, 王小旭, 吴石雨, 等. 基于Simulink−M文件混合编程方法的飞行器推力方案优化[J]. 北京理工大学学报, 2009, 29(10): 847−849. WANG Yue, WANG Xiaoxu, WU Shiyu, et al. Aircraft thrust scheme optimization hybrid program based on Simulink−M[J]. Transactions of Beijing Institute of Technology, 2009, 29(10): 847−849.

[17] DE WIT C C, OLSSON H, ASTROM K J, et al. A new model for control of system with fiction[J]. IEEE Transactions on Automatic Control, 1995, 40(3): 419−425.

(编辑 陈灿华)

Structure optimization and achievement of sub-micron optical motion platform

XU Cong1, DUAN Jian1, TANG Hao1, LI Shuai2

(1. State Key Laboratory of High Performance and Complex Manufacturing, Central South University, Changsha 410083, China; 2. School of Information Science and Engineering, Central South University, Changsha 410083, China)

In order to design a sub-micro platform driven by DC motor and reduce its motion errors as much as possible, an method which was based on hybrid simulation by Simulink−M and a stribeck friction model, the impact of ball screw and synchronous belt on the motion error was analyzed. The structure was optimized based on the analysis results and the demand. The motion platform was tested with the EMAC 200 controller and XL-80 laser interferometer system. The results show that the motion error is mainly affected by the ball screw’s lead, synchronous belt’s transmission ratio and their accuracy. Error will reduce when the lead decreases, ratio increases as well as their accuracy is improved. The error is within ±1.5 μm when the displacement is 1 mm and a 50 nm actual resolution can be achieved for this platform. The high-precision motion platform, as a complex nonlinear system, can be optimized based on hybrid simulation by Simulink−M.

precision motion platform; hybrid simulation by Simulink−M; structure optimization; error

TN252

A

1672−7207(2018)01−0080−07

10.11817/j.issn.1672-7207.2018.01.011

2017−03−10；

2017−05−21

国家自然科学基金资助项目(50975293)；中南大学研究生自主探索创新项目(2016zzts290) (Project(50975293) supported by the National Natural Science Foundation of China; Project(2016zzts290) supported by the Postgraduate Exploratory and Innovative Program of Central South University)

段吉安，教授，博士生导师，从事光电子器件制造技术与装备、机械设计理论与方法、精密运动控制研究；E-mail: duanjian@csu.edu.cn