燃爆类应急离机门作动器冲击强度分析

付春艳，曹立帅

(庆安集团有限公司 航空设备研究所，西安 710077)

0 引 言

应急离机门作动器结构简单、体积小，是飞机上应对紧急状况时的离机门安全开启设备，其性能的可靠程度对飞行员人身安全至关重要。因此，对应急离机门作动器可靠性的测试及强度分析显得尤为重要。

国内关于应急离机门作动器冲击强度分析的研究鲜有报道，只有少数关于应急离机轨迹和应急离机试飞的文献资料。其中刘洋等[1]对某型客机试飞员空中应急离机轨迹进行风洞试验研究，得出飞行速度、飞行高度、姿态角、离机初始速度对离机轨迹影响显著；孙庆元[2]对军用运输机空中应急离机试飞验证方法进行了探讨；赵晓军等[3]对飞机试飞中的应急离机安全措施进行了探讨。虽然美国以及欧洲飞机发展水平处于世界领先地位，但是关于应急离机门作动器冲击强度分析相关文献资料未有公开。综上所述，开展飞机应急离机门作动器冲击强度分析具有重要意义，对飞机空中离机系统的设计具有较高的价值。

柴象海等[4]采用LS-DYNA显式动力学有限元计算模型对空心瓦伦结构的冲击性能进行了数值模拟；田相克[5]基于MSC.Patran和MSC.Dytran对机电产品元件的抗冲击性能进行了分析，通过仿真对结构强度进行验证。LS-DYNA显式动力学适用于高速、超高速冲击问题，不易收敛。通过MSC.Patran前处理建模后，在MSC.Dytran中分析计算，计算结果再导入MSC.Patran系统进行结果分析，工作量大，不易操作。上述两种算法只适用于明确的冲击载荷条件下，对冲击过程的简单模拟。

本文基于气体平衡方程，引入气体膨胀做功的算法及功能转化的思想，将燃爆气压作功转换为活塞的初始冲击速度，然后采用瞬态动力学分析方法对活塞冲击外筒的过程进行模拟，并对某燃爆类应急离机门作动器冲击强度进行分析，并给出动强度的评判标准。

1 载荷转化

根据理想气体状态方程PV=nRT计算出应急离机门作动器活塞腔充满燃爆气体后的平衡气压。两腔气体平衡方程为

(1)

式中：P1为燃爆室峰值压力；P2为活塞腔充满气体后的平衡气压；V1为燃爆室体积；V2为活塞腔体积；T1为燃爆室气体温度；T2为活塞腔气体温度。

计算过程中气体温度变化忽略不计。应急离机门作动器结构如图1所示。

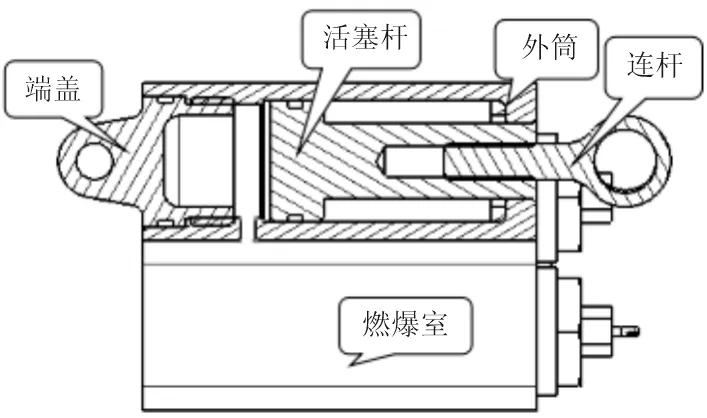
图1 应急离机门作动器结构示意图Fig.1 Structural diagram of actuator for emergency gate

燃爆气压进入活塞腔后推动活塞做功：

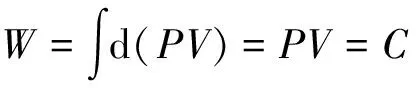
(2)

则

(3)

(4)

气体推动活塞做功介于C1与C2之间，取两者平均值作为活塞杆初始动能，根据功能转换原理(式(5))得出活塞杆与外筒碰撞瞬间的初始速度v0。采用瞬态动力学分析方法对活塞杆以初始速度v0撞击外筒的冲击过程进行模拟分析。

(5)

2 瞬态分析理论

2.1 大变形基本理论

大变形理论为瞬态分析的核心理论，其基本迭代过程如图2所示。

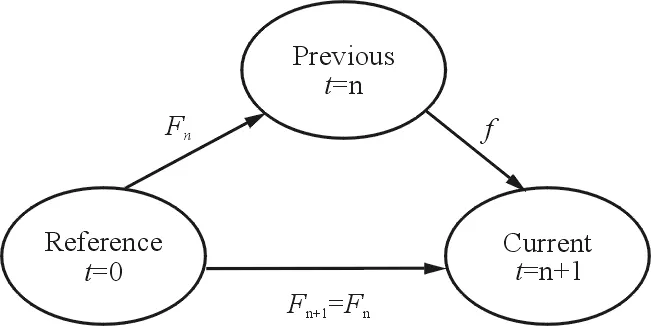
图2 大变形理论迭代示意图Fig.2 Iteration diagram of large deformation theory

拉格朗日方法中虚功原理方程为[6-7]

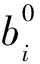
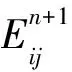
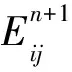
(6)

(7)

(8)

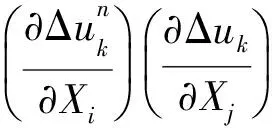
(9)

2.2 接触界面模拟

瞬态动力学方法对撞击物体和被撞物体分别建立有限元模型。通过位移协调条件与动量方程求解撞击载荷，本文在定义活塞杆-外筒之间的接触时采用罚函数法，其原理如下[8]：首先在每一个时间步前检查各从节点是否穿透主面，如果没有穿透，不做任何处理；如果穿透，则在该从节点与被穿透主面间引入一个较大的界面接触力，其大小与穿透深度、主面的刚度成正比。这在物理上相当于在两者之间放置一个法向弹簧，以限制从节点对主面的穿透，接触力称为罚函数值。“对称罚函数法”则是同时对每个主节点也作类似上述处理。

3 材料断裂强度计算公式

对于材料断裂强度的估算[9-10]如式(10)～式(15)所示。

对于高塑性材料，有

εf=-ln(1-Ψ)

(10)

σf=σb(1+Ψ)

(11)

对于低塑性材料，有

εf=ln(1+δ)

(12)

σf=σb(1+δ)

(13)

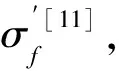
(14)

式中：R为颈缩处试件的半径；a为颈缩底部的曲率半径。

a/R之值可用下式估算：

a/R=0.76-0.94(1-εf)

另一种简单的修正函数[12]：

(15)

当0.15≤εf≤3.0时，式(15)有效；当εf≤0.15时，无需进行修正。

4 仿真计算

4.1 初始速度计算

某应急离机门作动器燃爆室最大峰值压力P1=15.34 MPa；根据式(1)求得平衡气压P2=11.42 MPa；继而由式(2)～式(4)可得气体推动活塞做功为860.89～1 155.64 J。取两者平均值作为活塞杆初始动能，根据功能转换原理即公式(5)得v0=15 m/s，采用瞬态动力学分析方法对活塞杆以v0=15 m/s的初始速度冲击外筒的过程进行模拟仿真。

4.2 有限元模型

瞬态动力学计算占用资源较多，因此需要对模型进行简化。根据模型对称性取四分之一进行计算，并采用六面体单元对几何模型进行网格划分，将各零件倒圆角处网格加密以提高计算精度。有限元模型如图3所示。

图3 有限元模型Fig.3 Finite element model

4.3 瞬态动力学计算

对称面施加对称约束,如图4(a)所示；对外筒一端压印面施加固定约束，如图4(b)所示；活塞杆圆柱面施加无摩擦约束(Frictionless Support)，如图4(c)所示。冲击过程中，外筒和活塞杆等效应力分布分别如图5和图6所示。

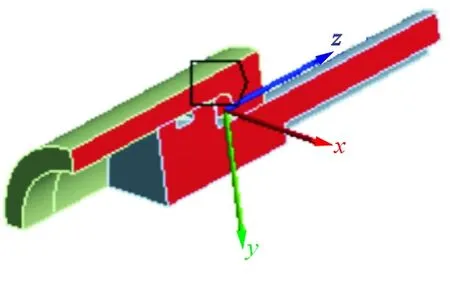
(a) 对称约束

(b) 固定约束

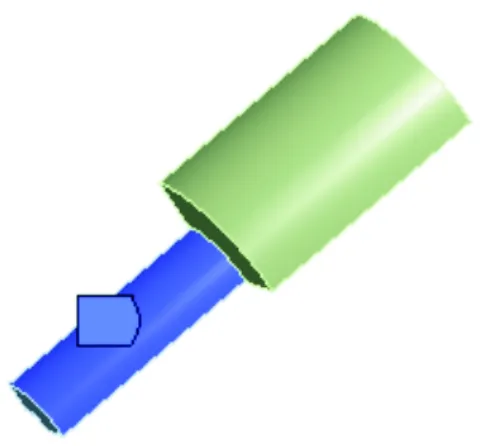
(c) 无摩擦约束图4 约束方式Fig.4 Constraint mode

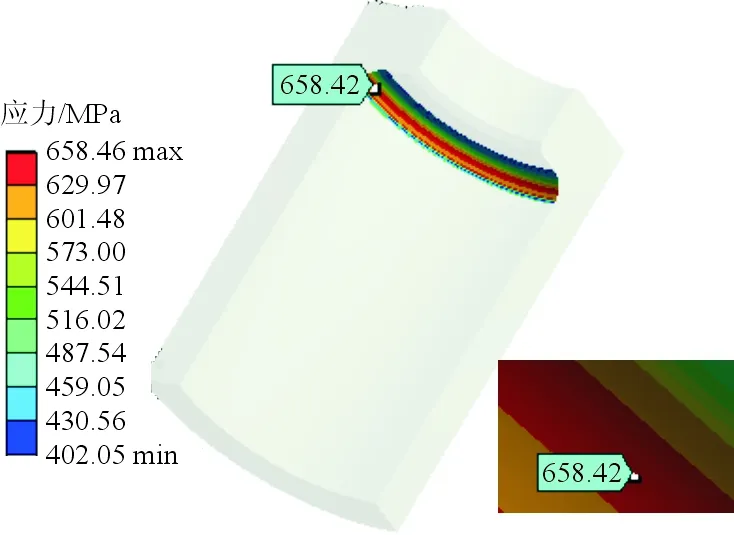
图5 外筒等效应力分布图(t= 0.000 041 s)Fig.5 equivalent stress distribution diagram of external cylinder(t= 0.000 041 s)

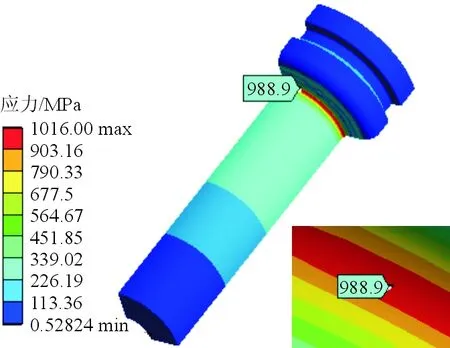
图6 活塞杆等效应力分布图(t= 0.000 031 s)Fig.6 Equivalent stress distribution diagram of piston rod(t= 0.000 031 s)

从图5～图6可以看出：外筒与活塞杆分别在0.000 041 s和0.000 031 s时刻出现最大等效应力，最大等效应力分别为658.42 MPa、988.90 MPa。

4.4 材料断裂强度仿真计算

外筒和活塞杆的材料均为0Cr17Ni4Cu4Nb，属于高塑性材料。根据式(10)和式(11)得：

εf=-ln(1-Ψ)=-ln(1-0.45)=0.597 8

σf=σb(1+Ψ)=1 080×(1+0.45)=1 566 MPa

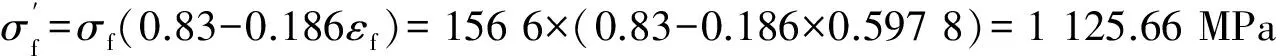
4.5 计算结果

某应急离机门作动器外筒和活塞杆冲击强度的计算结果如表1所示。

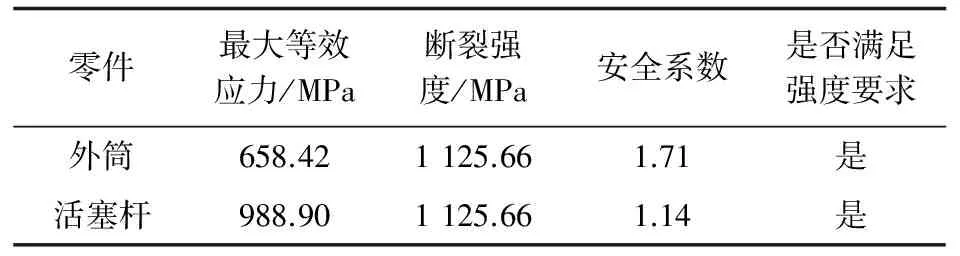
表1 某应急离机门作动器冲击强度计算结果Table 1 Calculation results of impact strength of an emergency gate actuator

从表1可以看出：某应急离机门作动器外筒和活塞杆最大等效应力均小于材料断裂强度，即安全系数均大于1，满足动强度要求。

5 结 论

(1) 本文基于功能转换原理将初始燃爆气压转换为初始冲击速度，适用于所有燃爆类作动筒初始冲击载荷的获取。

(2) 采用结构对称原理对作动器结构进行简化，易使用六面体单元对模型进行网格划分，可以简单准确地获取应力集中位置。

(3) 燃爆类应急离机门作动器活塞杆与外筒冲击部位附近的倒圆角处应力集中，为产品的危险部位，应尽可能避免或增大倒圆角半径。

[1] 刘洋, 周星. 民用飞机试飞员空中应急离机轨迹风洞实验研究[J]. 实验流体力学, 2015, 29(6): 54-58.

Liu Yang, Zhou Xing. Wind tunnel test study of air emergency escape trajectory for civil aircraft testpilots[J]. Experimental Fluid Mechanics, 2015, 29(6): 54-58.(in Chinese)

[2] 孙庆元. 军用运输机空中应急离机试飞验证方法探讨[J]. 飞行试验, 2004, 20(1): 37-41.

Sun Qingyuan. Discussion on flight test validation method of military aircraft in air emergency departure[J]. Flight Test, 2004, 20(1): 37-41.(in Chinese)

[3] 赵晓军, 史继斌, 许梦丽. 运输类飞机试飞安全保障技术研

究-ARJ21-700飞机适航审定试飞空中应急离机系统[J]. 中国科技信息, 2015(15): 49-51.

Zhao Xiaojun, Shi Jibin, Xu Mengli. Research on safety support technology for test flight of transport aircraft-ARJ21-700 airworthiness test flight test flight system[J]. China Science and Technology Information, 2015(15): 49-51.(in Chinese)

[4] 柴象海, 王志强, 冯锦璋. 扩散连接空心瓦伦结构抗冲击强度分析[J]. 航空科学技术, 2012(5): 18-21.

Chai Xianghai, Wang Zhiqiang, Feng Jinzhang. Impact strength analysis of hollow Valen steucture with diffusion connection[J]. Aeronautical Science and Technology, 2012(5): 18-21.(in Chinese)

[5] 田相克. 产品抗冲击强度分析的有限元建模及落球冲击试验仿真[J]. 机械强度, 2010, 32(6): 1022-1025.

Tian Xiangke. Finite element modeling of impact strength analysis of products and Simulation of drop impact test[J]. Mechanical Strength, 2010, 32(6): 1022-1025.(in Chinese)

[6] 赵海鸥. LS-DYNA动力分析指南[M]. 北京: 兵器工业出版社, 2003.

Zhao Haiou. LS-DYNA dynamic analysis guide[M]. Beijing: Ordnance Industry Press, 2003.(in Chinese)

[7] 白金泽. LS-DYNA3D理论基础与实例分析[M]. 北京: 科学出版社, 2005.

Bai Jinze. Theoretical basis and case study of LS-DYNA3D[M]. Beijing: Science Press, 2005.(in Chinese)

[8] 段成材. 谐波齿轮传动的瞬态动力学特性研究[D]. 重庆: 重庆大学, 2012.

Duan Chencai. Study on transient dynamic characteristics of harmonic gear drive[D]. Chongqing: Chongqing University, 2012.(in Chinese)

[9] 郑修麟. 材料的力学性能[M]. 2版. 西安: 西北工业大学出版社, 2000.

Zheng Xiulin. Mechanical properties of materials[M]. 2nd ed. Xi’an: Northwestern Polytechnical University Press, 2000.(in Chinese)

[10] 郑修麟. 切口件的断裂力学[M]. 西安: 西北工业大学出版社, 2005.

Zheng Xiulin. Fracture mechanics of notched parts[M]. Xi’an: Northwestern Polytechnical University Press, 2005.(in Chinese)

[11] Dieter G E Jr. Mechanical metallurgy[M]. New York: Mc-Graw-Hill Company, Inc, 1963.

[12] Dowling N E. Mechanical behavior of materials[M]. 2nd ed. USA: Prentice Hall, Upper Saddle River, New Jersey, 1999.