半环上线性方程的一些研究进展
2018-02-02王学平
王 学 平
(四川师范大学数学与软件科学学院, 四川 成都 610066)
1 问题的产生
所谓半环[1-2],就是指带有2个运算的代数系统L=(L,+,·,0,1),它满足:1)(L,+,0)是交换幺半群;2)(L,·,1)是幺半群;3)∀r,s,t∈L,r·(s+t)=r·s+r·t与(s+t)·r=s·r+t·r成立;4)∀r∈L,0·r=r·0=0成立;5)0≠1。如果半环的乘法还是交换的,则称该半环为交换半环。如果半环L满足对任意a,b∈L,a+b=0蕴含a=0与b=0,则称该半环为zerosumfree半环。半环这样的代数系统是大量存在的,我们熟知的代数系统环与域显然是半环的特例。如果定义∨=+,∧=·,则容易验证有界分配格是半环。如果定义max=+,把普通的加法定义为乘法,则易验证(R∪{-∞},+,·,-∞)也是半环,通常我们称该半环为max-plus代数或schedule代数[3-5]。显然,前面2个半环均为交换的zerosumfree半环。
如果半环L的元a满足:存在b∈L使得ab=ba=1,则称a是乘法可逆的,记U(L)={a:a是半环L上乘法可逆元},称b为a的可逆元,易见,a的可逆元b是唯一的,记为a-1。如果半环L的元a满足对任意b,c∈L,a+b=a+c蕴含b=c,则称元a是可消的。如果半环L的每个元都是可消的,则称半环L是可消的(cancellative semiring)。如果半环L的元a满足:对任意b,c∈L,ab=ac蕴含b=c,则称元a是乘法左可消的。类似可定义乘法右可消元。如果元a既是乘法左可消的又是乘法右可消的,则称a是乘法可消的。如果对任意a,b∈L,存在元r∈L使得a+r=b或a=b+r,则称半环L是yoked的(yoked semiring),称无零因子半环为整半环(entire semiring)[2]。如果半环L的元r满足:对任意a,b∈L,r=a+b蕴含r=a或r=b,则称元r是可加既约元[6]。
为描述如医疗诊断等复杂系统,1976年,Sanchez开始了完备Brouwer格上模糊关系方程的研究[7],给出了模糊关系方程有解的充要条件,并在有解时给出了模糊关系方程最大解的表述公式。从本质上来说,完备Brouwer格上的模糊关系方程就是有界分配格上线性方程,即方程A⊙x=b或
(1)
其中,A=(aij)m×n与b=(b1,b2,…,bm)T为已知的,而x=(x1,x2,…,xn)T是未知的。
1960年,为解决调度以及分离事件等问题,R.A.Cuninghame-Green开始研究max-plus代数上线性系统A⊙x=b或
(2)
其中,A=(aij)m×n与b=(b1,b2,…,bm)T为己知的,而x=(x1,x2,…,xn)T是未知的。max-plus代数上线性代数理论提供了用线性方法求解非线性问题的数学理论和方法,被广泛应用于生产问题、运输问题、资源分配及信息处理等[4-5],最典型的例子就是飞机的起飞时间问题的求解。
由于有界分配格和max-plus代数都是半环的特例,因此完备Brouwer格上模糊关系方程与max-plus代数上线性系统方程都是半环上线性方程的特例。因为域及有单位元的环也是特殊半环,所以大家熟知的经典线性方程也是半环上线性方程的特例。于是一个自然的问题就是:能否在半环上统一完备Brouwer格上模糊关系方程理论、max-plus代数上线性系统方程理论及大家熟知的经典线性方程理论等?也就是说, 我们能否建立半环上求解线性方程Ax=b或
(3)
的理论?其中,A=(aij)m×n与b=(b1,b2,…,bm)T为己知的,而x=(x1,x2,…,xn)T是未知的
以下分半线性空间、 矩阵的McCoy秩、 广义Cramer法则进行讨论, 未交代的概念及符号参见文献 [8]。
2 半线性空间
对经典线性方程组来说, 要刻画其解集,核心的问题就是寻找解空间的基,即方程组对应齐次组的基础解系。对max-plus代数上线性方程组的研究也揭示了这一规律。因此,要研究半环上线性方程(3)的解,我们首先来建立半环上线性空间,我们称半环上的线性空间为L-半线性空间(L-semilinear space)。其定义如下:
定义2.1[1-2]设L=〈L,+,·,0,1〉为半环,A=〈A,+A,0A〉为交换幺半群。如果外积*:L×A→A满足∀r,r′∈L,a,a′∈A,
1)(r·r′)*a=r*(r′*a),
2)r*(a+Aa′)=r*a+Ar*a′,
3)(r+r′)*a=r*a+Ar′*a,
4)1*a=a,
5)0*a=r*0A=0A,
则称〈L,+,·,0,1;*;A,+A,0A〉为左L-半模。类似可给出右L-半模的定义。
易见,如果(L,+,·,0,1)是有单位元的环且A是Albel群,则定义2.1是模的定义[9]。特别地,如果(L,+,·,0,1)还是域,则定义2.1退化为线性空间的定义[10-11]。
称半环L上的半模为L-半线性空间。这里的半模或是左L-半模,或是右L-半模。
例2.1 (a)设L=〈L,+,·,0,1〉是半环。对n≥1,令
其中(a1,a2,…,an)T表示(a1,a2,…,an)的转置。对任意的x=(x1,x2,…,xn)T,y=(y1,y2,…,yn)T∈Vn(L)和r∈L,定义
x+y=(x1+y1,x2+y2,…,xn+yn)T,r*x=(r·x1,r·x2,…,r·xn)T,
则Vn=〈L,+,·,0,1;*;Vn(L),+,0n×1〉是L-半线性空间。其中,0n×1=(0,0,…,0)T。设
类似地,按照以上方法定义运算“+”和“*”,则Vn=〈L,+,·,0,1;*;Vn(L),+,01×n〉是L-半线性空间,其中,01×n=(0,0,…,0)。
(b)设X≠∅,L=〈L,+,·,0,1〉是半环。令A=LX={f:f:X→L},对任意的f,g∈A及r∈R,定义
f(x)+Ag(x)=f(x)+g(x)及r*f(x)=r·f(x)对任意x∈X成立。
又设0A:X→L满足:对任意x∈X,0A(x)=0,则A=(L,+,·,0,1;*;A,+A,0A)是L-半线性空间。
以下在不会引起混淆的情况下,在L-半线性空间〈L,+,·,0,1;*;A,+A,0A〉中,对任意的r∈L,a∈A,我们将用ra代替r*a。我们引入线性相关、线性无关及基的概念。
定义2.2[12]设〈L,+,·,0,1;*;A,+A,0A〉为L-半线性空间,称表达式λ1a1+A…+Aλnan为A中向量组a1,…,an的线性组合。其中,λ1,λ2,…,λn∈L为标量(也称系数)。若向量x能表示为向量组a1,…,an的线性组合,则称向量x能被向量组a1,…,an线性表出(或线性表示)。
定义2.3[12]在L-半线性空间中,单个向量a是线性无关的。若向量组a1,…,an(n≥2)中的任意向量都不能被其余向量线性表出,则称该向量组是线性无关的。否则,称向量组a1,…,an是线性相关的。如果有无限个向量的向量组中任意有限个向量都是线性无关的,则称该向量组是线性无关的。
值得指出的是,按照定义2.3,单个的零向量也是线性无关的,这与经典线性代数很不相同。事实上,我们仅需注意到在经典线性代数中,对零空间没定义维数这一事实即可[11]。另一方面,由于半环中元关于乘法不一定可逆;因此,即使λi≠0,λj≠0(1≤i≠j≤n),我们也不能由λiai=λjaj推出向量组a1,…,an线性相关。为此,我们引入如下定义。

定义2.5[8]称非半线性相关的线性无关向量组a1,…,an(n≥2)为强线性无关向量组(a set of strongly linearly independent vectors)。
注2.1 半环上向量组线性相关或无关的定义[1,4,13-15]有很多。特别地,Celchlarova等在文献[15]中给出了bottleneck代数(一类特殊半环)上向量组线性相关的3组9种不同的定义方式,它们一般不是等价的[16]。
设G是L-半线性空间A的非空子集,如果L-半线性空间A中任意向量都能由集合G中向量线性表出,则称G是L-半线性空间A的生成集[13]。如果L-半线性空间A的元至多能被非空子集G中元以一种方式表出,则称G是自由的。显然,自由集一定是线性无关的。
定义2.6[2,17]称L-半线性空间A中线性无关的生成集为A的基。特别地,称L-半线性空间A的自由生成集为自由基(a free basis),称有自由基的L-半线性空间A为自由的。
易见,Vn与Vn都是自由的L-半线性空间。
与经典线性空间不同的是,半环上构成L-半线性空间的基的基数一般不唯一[12]。

因此,一个有趣的问题是:在什么样的条件下,L-半线性空间的基的基数一定唯一?
可以证明,定义在模糊代数{[0,1],max,min}及max-plus代数上的L-半线性空间的基的基数一定唯一[12,18]。2010年,赵姗和王学平给出了定义在交换的zerosumfree半环上L-半线性空间Vn的基的基数唯一的一个充分条件[6]。特别地,他们在2011年证明了:定义在完备并半环上的L-半线性空间Vn的基的基数是n的充要条件是1是并既约元[19]。这一结论被舒乾宇和王学平推广到了交换的zerosumfree半环上,进一步,舒乾宇和王学平还证明了:定义在交换的zerosumfree半环上L-半线性空间Vn的基的基数是相等的充要条件是Vn的每个向量能被基唯一表出[20]。该充要条件被谭宜家推广为如下定理[17]:
定理2.1 设A为交换半环L上有限生成的自由L-半线性空间,则A的基有相同基数的充要条件是每个基都是自由的。
设K(L)=max{t∈N:L-半线性空间V1有t个元的基}。谭宜家还证明了下面定理[17]:
定理2.2 设L为交换半环,则下面条件等价:
1)K(L)=1;
2)对任意u,v∈U(L),1=u+v蕴含u∈U(L)或v∈U(L);
3)有限生成的自由L-半线性空间A的任意两个基有相同的基数。
由于Vn是有限生成的自由L-半线性空间,因此由定理2.2易得下面推论。
推论2.1[17]设L为交换半环,则K(L)=1的充要条件是L-半线性空间Vn的基的基数是n。
2013年,在交换的zerosumfree半环L上,Kanan等[21]证明了:L-半线性空间Vn的基的基数是n的充要条件是L-半线性空间V1的基的基数是1。2014年,该结论被推广到了交换半环上:
定理2.3[22]设L为交换半环,则L-半线性空间Vn的每个基有相同基数的充要条件是Vn的每个向量可被基惟一线性表出。
定理2.4[22]设L为交换半环,则L-半线性空间Vn的每个基的基数是n的充要条件是V1的基的基数是1。
由推论2.1与定理2.4易证下面推论成立。
推论2.2 设L为交换半环,则K(L)=1的充要条件是V1的基的基数是1。
值得指出的是,Kim等1980年研究半环上L-半线性空间Vn时把空间的极小生成集(a minimal spanning set)定义为Vn的基(注:这里所说的极小,是从集合包含来说的),由此证明了定义在模糊代数{[0,1],max,min}上有限生成空间的任意2个基的基数是相等的[13]。
3 矩阵的McCoy秩
与经典线性代数一样,矩阵的秩对判别线性方程组(3)是否有解特别重要。对半环上矩阵的秩进行研究的论文较早见于Kim等[13],他们用矩阵的行空间与列空间的最小生成集(the smallest possible size of a spanning set)来定义矩阵的秩。即,如果该2个空间的最小生成集的基数相等就定义这个基数为矩阵的秩,否则分别称为矩阵的行秩与列秩。2010年,借助于双行列式,Perfilieva等[26]给出了矩阵秩的另一种定义方式。为叙述方便,先给出下面定义。
定义3.1[23]设L为半环,对任意b,c∈L,如果b=c,则定义(b,c)≡0。设半环L是可消的,对任意a∈L,如果存在a+,a-∈L使a+a-=a+,则定义a≡(a+,a-)。
定义3.2[8]设(a,b),(c,d)∈V2(L)。定义:
1)(a,b)≈(c,d)当且仅当存在r∈L使a+r=c,b+r=d或a=r+c,b=r+d成立;
2)(a,b)(c,d)=(a(c,d),b(c,d))=((ac,ad),(bc,bd))=(ac+bd,ad+bc)。
以下设L为半环,记Mm×n(L)={(aij)m×n:aij∈L}。特别,记Mn(L)=Mn×n(L),用In表示n×n单位矩阵。矩阵的乘法、加法及数乘与经典线性代数中一样,不再赘述。
定义3.3[24]设A∈Mm×n(L),用P与Q分别表示{1,2,…,n}的偶置换与奇置换之集。定义矩阵A的双行列式det(A)为序对
det(A)=(det1(A),det2(A))。
其中,
由定义3.1易见,det(A)≢0当且仅当det1(A)≠det2(A)。
注3.1 在文献[25]中,|A|+=det1(A),|A|-=det2(A),因此,det(A)=(|A|+,|A|-)。
设A∈Mm×n(L),B为A的s×s子矩阵,1≤s≤min{m,n},称det(B)为矩阵A的s阶子式。
下面是Perfilieva与Kupka给出的矩阵秩的定义[26]。
定义3.4 设A∈Mm×n(L),称A的不为零的最大子式的阶s为矩阵A的秩,记矩阵A的秩为r(A)。
用Ab表示线性方程组(3)系数矩阵A的增广矩阵,其中b=(b1,b2,…,bm)T。于是基于定义3.4,我们有下面判定半环上线性方程组(3)有解的Kronecker-capelli定理。
定理3.1[26]在交换半环L上,如果线性方程组(3)有解,则r(A)=r(Ab)。
文献[26]中例2.1告诉我们,定理3.1的逆一般不成立,也就是说,定理3.1仅能用于判别线性方程组(3)无解的情况。为此,舒乾宇和王学平[27]对定义3.4进行了如下改造。
定义3.5[20]如果L-半线性空间A的每个基的基数相等,则称基的基数为A的秩或维数,记为dimA。
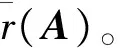
应该指出的是,定义3.4与定义3.6本质上是不一样的。


(x,y)=x1y1+x2y2+…+xnyn。
易见,对任意的x,y∈Vn及k∈L,(x,y)=(y,x),k(x,y)=(kx,y)=(x,ky)。
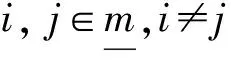
于是,我们有下面判定半环上线性方程组(3)有解的Kronecker-capelli定理。
定理3.2[27]在交换半环L上,如果U(L)=L
虽然定理3.2是充分必要的,但遗憾的是,在定理的条件下,如果线性方程组有解,则仅有唯一解,这显然与客观事实不符,因为我们容易找到有若干解的线性方程组。为此,我们引入矩阵的McCoy秩,以期获得更符合实际的判定半环上线性方程组有解的Kronecker-capelli定理。
用A≡0表示A={(a,b)∈V2(L):a=b}。
定义3.8[23]设A是半环L上m×n矩阵。矩阵A的McCoy秩是最大的t,它满足:任意y∈V2(L),如果y∈AnnihV2(L)(Ft(A)),则y≡0。其中,Ft(A)是A的所有t×t子阵的双行列式之集,AnnihV2(L)(Ft(A))={r∈V2(L):rFt(A)≡0}。
易见,矩阵的McCoy秩是环上矩阵McCoy秩的推广。由定义3.8容易证明A与AT的McCoy秩是相等的。
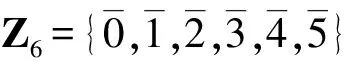
考虑半环L上线性代数系统

于是有下面两个定理[23]:
定理3.3 设L为交换的可消半环,A∈Mn(L),则矩阵A的McCoy秩小于n的充要条件是方程组Ax≡0有非平凡解。
定理3.4 在交换的可消的yoked整半环L中,设A∈Mn(L),且n≥2,则下面结论等价:
1)矩阵A的列向量或是线性相关的或是半线性相关的;
2)方程组Ax≡0有非平凡解;
3)矩阵A的McCoy秩小于n;
4)det(A)≡0。
值得指出的是,上面定理3.4除了使用McCoy秩外,与经典线性代数中结论是一致的。不过,其对半环的要求太强。另外,目前还没有用McCoy秩描述判别半环上线性方程组有解的Kronecker-capelli定理的报道。
4 广义Cramer法则
为叙述方便,以下先回忆可逆矩阵的概念[28]。
定义4.1 设A∈Mn(L),如果存在矩阵B∈Mn(L)使得AB=In,则称矩阵A是右可逆的;类似地,可定义左可逆矩阵。如果矩阵A既是左可逆的又是右可逆的,则称A是可逆矩阵。
1984年,Reurenauer等[28]证明了如下定理。
定理4.1 在交换半环L上,设A,B∈Mn(L),如果AB=In,则BA=In。
定理4.2[25]在交换半环L上,设A,B∈Mn(L),如果AB=In,则
1+|A|+|B|-+|A|-|B|+=|A|+|B|++|A|-|B|-。
由行列式的定义3.3及定理4.1及4.2知下面推论成立。
推论4.1 在交换的可消半环L上,如果A是可逆矩阵,则det(A)≢0。
由定理4.1即知,右(左)可逆矩阵一定是可逆矩阵。记可逆矩阵A的逆矩阵为A-1,设V(L)={a∈L:如果存在b∈L使得a+b=0},则有下面定理。
定理4.3[22]在交换半环L上,如果A是可逆矩阵,则|A|+∈V(L)或|A|-∈V(L)。
在经典线性代数中,当方程组的系数矩阵非奇异时可用Cramer法则描述线性方程组的唯一解。研究求解半环上线性方程唯一解的Cramer法则的工作最早见于文献[29]。田振际等[29]在系数矩阵可逆的条件下给出了求解完全分配格(一类特殊半环)上线性方程唯一解的Cramer法则。2004年,Han等[30]研究了坡(incline,一类特殊半环)上线性方程的Cramer法则。由于完全分配格是坡,从而推广了田振际等[29]所获得的Cramer法则。2007年,谭宜家[31]又在交换的zerosumfree半环上推广了Han等的工作,即,在系数矩阵可逆的条件下给出了求定义在交换的zerosumfree半环上线性方程组唯一解的Cramer法则。
设L=〈L,+,·,0,1〉为半环,如果一一映射ε:L→L满足:对任意a,b∈S,ε(ε(a))=a,ε(a+b)=ε(a)+ε(b),ε(ab)=aε(b)=ε(a)b;且对任意a∈V(S),ε(a)=-a,则称一一映射ε为ε函数。
设L=〈L,+,·,0,1〉为有ε函数的交换半环,A=(aij)∈Mn(L),定义
其中:Sn是n次对称群;t(σ)为排列σ的逆序数。显然Sn=P∪Q。
设a1,a2,…,an为线性方程组(3)的系数矩阵A∈Mm×n(L)的列向量,于是借助于上面的ε函数,谭宜家[32]在交换半环上给出了系数矩阵可逆条件下求解线性方程组的Cramer法则。
定理4.4[32]设L为有ε函数的交换半环,m=n,如果系数矩阵A是可逆的,则线性方程组(3)有唯一解
x=(d-1d1,d-1d2,…,d-1dn)T。
其中,d=detε(A),di=detε(Di),Di=(a1,…,ai-1,b,ai+1…,an)是用常值向量b替换系数矩阵的第i列所得。
上面定理的成立首先依赖于交换半环L有ε函数,而廖亚林和王学平在文献[33]中举例说明并不是所有交换半环都有ε函数(参见文献[33]第478页最后一段)。其次,定理还依赖于系数矩阵A是可逆阵。众所周知,在经典线性代数理论中,矩阵A可逆等价于它的行列式不等于0。然而,在交换半环上,由矩阵A的行列式det(A)≢0不一定能推出A是可逆的。

推论4.1与例4.1说明det(A)≢0的矩阵比可逆矩阵要广得多。因此,一个自然的问题就是:在交换的可消半环上,当系数矩阵A的行列式det(A)≢0时,能否建立求解方程组(3)的Cramer法则?
我们有下面结论。

det(Di)≈det(A)ri。
其中,Di=(a1,…,ai-1,b,ai+1…,an)。而且,在方程组(3)有解时有唯一解(r1,r2,…,rn)T。
由定理4.5成立的条件易见,关于求方程组(3)唯一解的Cramer法则的研究并没完结。
5 结论
众所周知,半环上线性代数包含的内容还有许多,如行列式[8,25]、空间维数公式[34]、可逆矩阵(见文献[6,22,28,30-33]),以及连接两个基的过度矩阵(transition matrix)[17]等。应该说,这些内容除行列式及可逆矩阵外研究还很不充分,如,目前还仅仅在1是可加既约元的条件下给出了维数公式。特别地,判别半环上线性方程组有解的Kronecker-capelli定理作为半环上线性代数的核心内容,也还没有一个更一般的结论。
四川师范大学数学与软件科学学院舒乾宇博士阅读了论文初稿,并提出修改意见,在此致以诚挚的谢意。
[1]ZIMMERMANN U. Linear and combinatorial optimization in ordered algebraic structures[M]//Ann Discrete Mathematics: 10. North Holland:[s.n.], 1981.
[2]GOLAN J S. Semirings and Their Applications[M]. Dordrecht/Boston/London: Kluwer Academic Publishers, 1999.
[3]BACCELLI F L, COHEN G, OLSDER G J, et al. Synchronization and Linearity[M]. Chichester, New York: J. Wiley and Sons, 1992.
[4]BUTKOVI P. Max-linear Systems: Theory and Algorithms[M]. [S.l.]: Springer, 2010.
[5]CUNINGHAME-GREEN R A. Minimax algebra[M]//Lecture Notes in Economics and Mathematical Systems. Berlin: Springer, 1979.
[6]ZHAO Shan, WANG Xueping. Invertible matrices and semilinear spaces over commutative semirings[J]. Information Sciences, 2010, 180: 5115.
[7]SANCHEZ E. Resolution of composite fuzzy relation equations[J]. Information and Control, 1976, 30: 38.
[8]WANG Xueping, SHU Qianyu. Bideterminant and rank of matrix[J]. Soft Computing, 2014, 18: 729.
[9]MCDONALD B R. Linear Algebra over Commutative Rings[M]. New York: Marcel Dekker, 1984.
[10]HUNGERFORD T W. 代数学[M].冯克勤译.1版. 长沙:湖南教育出版社, 1985.
[11]北京大学数学系几何与代数教研室代数组. 高等代数[M]. 北京:高等教育出版社, 1988.
[12]DI NOLA A, LETTIERI A, PERFILIEVA I, et al. Algebraic analysis of fuzzy systems[J]. Fuzzy Sets and Systems, 2007, 158: 1.
[13]KIM K H, ROUSH F W. Generalized fuzzy matrices[J]. Fuzzy Sets and Systems, 1980, 4: 293.
[14]GONDRAN M, MINOUX M. Linear algebra in dioïds: a survey of recent results[J]. Ann Discrete Mathematics, 1984, 19: 147.
[15]CECHLAROVA K, PLAVKA J. Linear independence in bottleneck algebras[J]. Fuzzy Sets and Systems, 1996, 77: 337.
[16]肖梅, 王学平. 交换半环上向量不同线性无关性定义间的关系[J]. 模糊系统与数学, 2014, 28 (6): 29.
[17]TAN YiJia. Bases in semimodules over commutative semirings[J]. Linear Algebra and its Applications, 2014, 443: 139.
[19]ZHAO Shan, WANG Xueping. Bases in semilinear spaces over join-semirings[J]. Fuzzy Sets and Systems, 2011, 182: 93.
[20]SHU Qianyu, WANG Xueping. Bases in semilinear spaces over zero-sumfree semirings[J]. Linear Algebra and its Applications, 2011, 435:2681.

[22]SHU Qianyu, WANG Xueping. The cardinality of bases in semilinear spaces over commutative semirings[J]. Linear Algebra and its Applica- tions, 2014, 459: 83.
[23]SHU Qianyu, WANG Xueping. The applications of the bideterminant of a matrix over commutative semirings[J]. Linear and Multilinear Algebra, 2017, 65: 1462.
[24]KUNTZMAN J, Théorie des réseaaux graphes[M]. Paris:Dunod (Libraire), 1972.
[25]POPLIN P L, HARTWIG R E. Determinantal identities over commutative semirings[J]. Linear Algebra and its Applications, 2004, 387: 99.
[26]PERFILIEVA I, KUPKA J. Kronecker-capelli theorem in semilinear spaces[C]//Computational Intelligence-Foundations and Applications-international Flins Conference, World Scientific. Emei and Chengdu:[s.n.], 2010: 43.
[27]SHU Qianyu, WANG Xueping. Standard orthogonal vectors in semilinear spaces and their applications[J]. Linear Algebra and its Applica-tions, 2012, 437: 2733.
[28]REUTENAUER C, STRAUBING H. Inversion of matrices over a commutative semiring[J]. Journal of Algebra, 1984, 88: 350.
[29]田振际, 严克明, 李敦刚, 等. 完全分配格上的矩阵的行列式[J]. 甘肃理工大学学报, 2002, 28(4): 115.
[30]HAN S C, LI H X. Invertible incline matrices and Cramer’s rule over incline[J]. Linear Algebra and its Applications, 2004, 389: 121.
[31]TAN Yijia. On invertible matrices over antirings[J]. Linear Algebra and its Applications, 2007, 423: 428.
[32]TAN Yijia. On the invertible matrices over commutative semirings[J]. Linear and Multilinear Algebra, 2013, 61: 710.
[33]LIAO Yalin, WANG Xueping. Note on invertible matrices over commutative semirings[J]. Linear and Multilinear Algebra, 2016, 64: 477.
[34]SHU Qianyu, WANG Xueping. Dimensional formulas of semilinear subspaces over semirings[J]. Linear and Multilinear Algebra, 2014, 62:1475.
特约专家介绍

王学平(1965—),男,汉族,四川遂宁人,中共党员,理学博士,四川省学术和技术带头人,四川省二级教授,博士生导师。1999年博士毕业于四川大学数学学院。现为美国《数学评论》评论员、《四川师范大学学报(自然科学版)》主编、中国系统工程学会模糊系统与数学委员会理事、中国运筹学会模糊信息与工程学会委员会常务理事、四川省数学学会理事。主要从事格理论及其应用、不确定性的数学理论、半环理论及其应用、max-plus代数上线性代数理论与矩阵理论等的研究。已在《中国科学》《数学学报》《数学年刊》《计算数学》《数学进展》《高等学校计算数学学报》《高校应用数学学报》及《SCIENCE CHINA Mathematic》《Fuzzy Sets and Systems》《Information Sciences》《Indian J. pure appl. Math.》《Int. J. General Systems》《Soft Computing》《Linear Algebra and Its Applications》《Linear and Multilinear Algebra》《Studia Logica》《Order》《Computers and Mathematics with Applications》等国内外重要学术刊物上发表论文50余篇。已主持国家自然科学基金面上项目及四川省杰出青年科技基金各2项、教育部高校博士点基金资助项目1项,参与国家自然科学基金面上项目1项。
