关于Lucas数立方与二项式数的卷积公式

陈 小 芳

(渭南师范学院数理学院, 陕西 渭南 714099)

1 预备知识与结论

Lucas数列以及二项式系数的各种性质一直都是组合数学和数论中引得众多专家、学者关注的课题，而包含Lucas数的恒等式及包含二项式系数的恒等式更是引起国内外学者的研究兴趣。

(1)

对于l(k,m,n)的计算，文献[1]研究了广义杨辉三角与Lucas数列的卷积l(k,1,n)，得到了m=1的情形，即：l(k,1,n)=2kLn+2k，文献[2]讨论了杨辉三角与Lucas数列的卷积l(k,1,n)，给出了m=2的情形，证明了

本文讨论l(k,m,n)当m=3时的情形，得到了二项式系数与Lucas数立方的一个恒等式，证明了下面的定理1。

(2)

其中的L3k+2n和Ln-k分别为第3k+2n个和第n-k个Lucas数。

2 定理1的证明

由此可知

(3)

由式(3)及式(1)可知

(4)

由二项式定理可知：

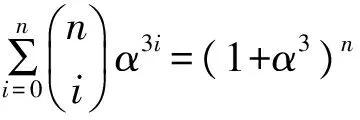
(5)

(6)

(7)

(8)

将式(5)、(6)、(7)、(8)代入式(4)得

l(k,3,n)=α3k·(1+α3)n+3(-1)kαk·(1-α)n+3(-1)kβk·(1-β)n+β3k·(1+β3)n。

(9)

又

1-α=β，1-β=α，1+α3=2α2，1+β3=2β2，

将其代入式(9)有

l(k,3,n)=α3k(1+α3)n+3(-1)kαk(1-α)n+3(-1)kβk(1-β)n+β3k(1+β3)n=α3k(2α2)n+3(-1)kαkβn+3(-1)kβkαn+β3k(2β2)n= 2nα3k+2n+3(-1)kαkβn+3(-1)kβkαn+2nβ3k+2n。

(10)

当k≥n时，

l(k,3,n)=2n(α3k+2n+β3k+2n)+3(-1)kαnβn(αk-n+βk-n)= 2n(α3k+2n+β3k+2n)+3(-1)k+n(αk-n+βk-n)= 2nL3k+2n+3(-1)k+nLk-n。

(11)

同理k

l(k,3,n)=2n(α3k+2n+β3k+2n)+3(-1)kαkβk(αn-k+βn-k)= 2n(α3k+2n+β3k+2n)+3(-1)k+k(αn-k+βn-k)= 2nL3k+2n+3Ln-k。

(12)

综合式(11)、(12)得

[1]晁晶晶.广义杨辉三角形与Lucas数列的关系研究[J].新乡学院学报(自然科学版),2011,28(3):196.

[2]陈小芳.Lucas数列与杨辉三角形的又一关系[J].江西科学,2013,31(3):287.

[3]陈小芳.Lucas数列中素因子2的指数[J].首都师范大学学报(自然科学版),2013,34(5):6.

[4]陈小芳.Lucas数的标准分解式中素因子3的指数[J].贵州师范大学学报(自然科学版),2013,31(4):45.

[5]陈小芳.Lucas数的标准分解式中素因子7的指数[J].贵州师范大学学报(自然科学版),2015,33(4):75.

[6]陈小芳.Lucas数列关于模的模数列的周期[J].贵州师范大学学报(自然科学版),2015,33(6):76.

[7]陈小芳.Lucas数列的模数列的周期性[J].首都师范大学学报(自然科学版),2015,36(5):11.

[8]于鸿，郜舒竹.广义Fibonacci等距子列关于模fm的模数列的周期[J].首都师范大学学报(自然科学版),2010,31(5):212.

[9]陈小芳.Fibonacci数与杨辉三角形的又一关系[J].首都师范大学学报(自然科学版),2014,35(3):1.

[10]晁晶晶.广义杨辉三角形与Fibonacci数列的一个关系[J].首都师范大学学报(自然科学版),2011，32(2):11.

[11]杨海,李博,高晓梅.二项式系数与Fibonacci数立方的一个关系[J].纺织高校基础科学学报,2015,28(4):365.

[12]OHTSUKA H,NAKAMURA S.On the sum of reciprocal Fibonacci numbers[J].The Fibonacci Quart-erly,2009,47(4):153.

[13]WANG A Y Z,ZHANG F.The reciprocal sums of even and odd terms in the Fibonacci sequence[J]. Journal of Inequalities and Applications.2015,2015(1):1.

[14]WANG A Y Z, LIU R N. Sums of products of two reciprocal Fibonacci numbers[J]. Advances in Difference Equations, 2016(1):1.

[15]SARAH H Holliday, Takao Komatsu. On the sum of reciprocal generalized Fibonacci numbers[J].Integers,2011,11(4):441.

[16]MA Rong, ZHANG Wenpeng. Several identities involving the Fibonacci numbers and Lucas numbers [J]. The Fibonacci Quarterly,2007, 45(2):164.

[17]ZHANG Guojie. The infinite sum of reciprocal of the Fibonacci numbers [J].Journal of Mathematical Research & Exposition,2011,31(6):1030.