高斯核的一般误差估计
2018-02-02韩永杰
韩永杰,陈 洁,2
(1.西华大学理学院,四川 成都 610039; 2.波鸿大学数学系,德国 北莱茵-威斯特法伦州 波鸿市 44787-44894)



令C(X)表示定义在X上的连续函数的全体,并赋予范数
当H是C(X)中的紧子集,且学习过程发生在H中,则称H为假设空间。

给定一个假设空间H,任意函数f∈H在H中的误差
ΕH(f)=Ε(f)-Ε(fH)
称为正规误差。可以看出对任意f∈H有ΕH(f)≥0,且ΕH(fH)=0。
根据最小二乘误差和正规误差的定义,有
Ε(fz)=ΕH(fz)+Ε(fH)。
(1)
考虑和式ΕH(fz)+Ε(fH)[2-3],第1项ΕH(fz)称作样本误差[4-5],第2项Ε(fH)和假设空间相关,但是独立于样本z,称作逼近误差[6]。
我们的目标是计算Ε(fz),等式(1)把目标转化成两个不同的问题:计算样本误差和逼近误差。注意到第1个问题是在假设空间H上提出的,第2个问题和样本z无关。固定H,样本误差随着采样点数目m的增加而减少;固定样本点数目,逼近误差会随着假设空间H的增大而减少,同时样本误差会增大。第二个特征被称作偏差-方差平衡[7-8]。
本文利用样本误差ΕH(fz)和逼近误差Ε(fH)的已有结果,将最小二乘误差Ε(fz)统一为一个表达式。
1 预备知识和主要结果
令X表示距离空间,如果对于映射K:X×X→R满足以下3个条件:
1)K(x,t)=K(t,x),任意x,t∈X;
2)矩阵(K(xi,tj))k×k是半正定的,xi,tj∈X;
3)映射K是连续的,则称K是Mercer核。

〈Kx,g〉K=g(x),∀x∈X,g∈HK,
称HK是再生核希尔伯特空间。HK是由连续函数构成的空间,‖·‖K是由内积诱导出的范数,且映射IK:HK→C(X)是有界的嵌入映射[9]。
在机器学习中,假设空间一般是Mercer核生成的再生核希尔伯特空间中的球。在以下部分我们默认IK(BR)为假设空间,其中BR={f:f∈HK,‖f‖K≤R}。
令s>0,Sobolev空间Hs定义如下:
Hs(Rn)={f:f∈L2(Rn), ‖f‖Hs<∞},

集合K是赋范线性空间(X,‖·‖)的一个子集,对任意ε>0,集合K的ε-势定义如下:
Ne(K)=min{N:z1,…,zN∈Rm,e(K,{z1,…,zN})≤ε}。


Zhou等研究了高斯核学习各向同性索伯列夫空间Hs的样本误差和逼近误差的收敛阶[6],但是没有给出最小二乘误差的收敛阶。本文在添加适当条件后,得到了最小二乘误差的估计。
在下文中,符号C表示不同位置可能不同的正常数。
定理A[11]令集合H是巴拿赫空间C(X)上的M-有界紧子集(即对任意的x∈H,都有M>0,使得x≤M),则对于任意的ε>0,

下面给出本文的主要结论。
定理1 令R>0,f(x)∈Hs(X),c0=4n(6n+2),当

E(f)≤C(lnR)-s/8。

注:定理1、2中的最小二乘误差估计并不是最优的,但将其统一为一个表达式可方便实际中的应用。
2 主要结论的证明
定理1的证明。已知假设空间的半径为R,则逼近误差的收敛阶是显然的。
下面计算样本误差。由假设空间是IK(BR),可以令M=R。根据定理A,有
(2)

(3)
其中c0=4n(6n+2)。对式(3)两边作取指数运算,可以得到
那么式(2)就可以化为
进一步化简得到
(4)
根据微分中值定理和f(x)=ex的单调递增性质有
即
根据上式,直接计算可得
(5)
化简式(5)
(6)

(7)

根据定理A、B,综合可得最小二乘误差为
E(f)≤C(lnR)-s/8。
定理2的证明。先考虑样本误差。由于假设空间是IK(BR),不妨取M=R。类似定理1的证明过程,可以得到
令
(8)
其中c2>1。式(8)通过移项化简为
(9)
对式(9)两边同时作取对数运算,得到
根据拉格朗日中值定理,有

当ε≤16R2e-(1/c0)1/(n+1)时,有
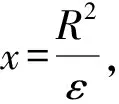
根据定理A、B,最小二乘误差为:
[1]CUCKER F, SMALE S. On the mathematical foundations of learning[J]. Bulletin of the American Mathematical Society, 2001, 39(1): 1.
[2]COX D D. Approximation of least squares regression on nested subspaces[J]. Annals of Statistics, 1988, 16(2): 713.
[3]NIYOGI P, GIROSI F. On the relationship between generalization error, hypothesis complexity and sample complexity for radial basis functions[J]. Neural Computation, 1989, 8(9): 819.
[4]DEVROYE L, GYORFI L, LUGOSI G. A probabilistic theory of pattern recognition[M]. Berlin: Springer-Verlag, 1996.
[5]ANTHONY M, BARTLETT P. Neural network learning: theoretical foundations[M]. New York: Cambridge University Press, 1999.
[6]CUCKER F, ZHOU D X. Learning theory: an approximation theory viewpoint[M]. New York: Cambridge University Press, 2007.
[7]GOLUB G, HEAT M, WAHBA G. Generalized cross-validation as a method for choosing a good ridge parameter[J]. Technometrics, 1979, 21(2): 215.
[8]BISHOP C M. Neural networks for pattern recognition[M]. New York: Oxford University Press, 1996.
[9]ARONSZAJN N. Theory of reproducing kernels[J]. Transactions of the American Mathematical Society, 1950, 68(3): 337.
[10]MAIOROV V E. Kolmogorov’s (n,δ)-widths of spaces of smooth functions[J]. Sbornik Mathematics, 1994, 79(2): 265.
[11]ZHOU D X. The covering number in learning theory[J]. Journal of Complexity, 2002, 18(3): 739.
[12]SMALE S, ZHOU D X. Estimating the approximation error in learning theory[J]. Analysis and Applications, 2003, 1(1): 17.
