间缝式开口隧道缓冲结构气动特性分析

王英学，常乔磊，任文强，张罗逊



间缝式开口隧道缓冲结构气动特性分析

王英学，常乔磊，任文强，张罗逊

(西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031)

采用通用CFD工程分析软件，对高速列车突入有间缝式开口缓冲结构的隧道的空气动力学特性进行三维数值模拟。分析间缝式单、双开口缓冲结构的最优结构形式，采用模型试验和现场测试方法，对数值分析结果进行比较验证。研究结果显示：与常规既有的缓冲结构相比，间缝式开口缓冲结构对压力梯度的降低效率更高，经济性更好。从控制隧道出口微气压波的需要，提出应综合考虑单位米长降低率与总降低率，来选择缓冲结构的形式及参数。

隧道；缓冲结构；间缝；压力梯度；缓解效率

高速列车进入隧道时，列车前方空气受压，会形成压缩波。该压缩波沿列车运行方向以声速传播，到达隧道出口，由于传播空间突然急剧变大，会产生微气压波向隧道外扩散，形成音爆现象，对隧道口周围环境造成影响[1]。研究表明：微压波大小与到达隧道出口时的压缩波梯度大小成正比[2]，降低压缩波在隧道入口产生的压力梯度，就可实现控制隧道出口微压波峰值的目的。本文将以隧道内压缩波的压力梯度为参考指标，探讨分析一种新型缓冲结构控制微气压波的效果。降低压缩波在隧道入口产生的压力梯度的措施主要包括:隧道入口处设置缓冲结构、隧道内设置竖井、利用救援通道作为泄压通道、双线隧道间联络通道、优化列车车头形状等。国内外有许多学者对缓冲结构控制微气压波的效果及结构参数设计方法开展研究，得到了很多重要结论。骆建军等[3]通过数值模拟得出缓冲结构物能有效地降低压力波和微气压波前的压力梯度的结论。刘佩斯[4]结合京沪高速铁路隧道项目研究了竖井对高速铁路隧道气动效应的影响，给出了与列车长度,隧道长度和车速有关的竖井最优位置选择公式。骆建军等[5]研究了高速铁路并联隧道横通道对隧道内压力变化的影响，得出在相同条件下，竖井的降压效果最好，横通道次之，避洞的降压效果最差。赵文成[6]通过模型试验和数值推导对典型缓冲结构(断面扩大无开口型缓冲结构、喇叭型缓冲结构和开口型缓冲结构)进行了全面系统的参数研究。刘善华[7]利用数值模拟和大比例尺高速列车动模型试验系统研究了高速铁路隧道洞口顶部开口缓冲结构在不同运营速度下的最优开口率及开口位置。Howe等[8−10]对等截面和变截面隧道多开口缓冲结构参数进行分析，提出了多开口缓冲结构优化参数，并指出缓解效率是有限的，达到限值后不会随长度增加而提高。LIU等[10]对喇叭型缓冲结构、断面扩大型缓冲结构及削竹式洞口的气动特性进行了分析评价。上述学者对缓冲结构进行研究，主要针对总体缓解效果，并未考虑缓冲结构单位长度的缓解效率，本文将从此角度出发开展研究工作，为缓冲结构形式的优选提供依据。在隧道入口处设置缓冲结构由于其附加工程量少、控制微气压波效果明显，因此被规范采用。目前，开口型缓冲结构的开口位置，主要设置在顶部或侧部。侧部开口缓冲结构开口宽度一般在2 m左右，顶部开口缓冲结构的开口宽度一般在4 m左右[12]。为了达到较好的缓解微气压波效果，需要较高的开口率。在增加缓冲结构开口长度的同时，缓冲结构的总体长度也要相应加长，于是就会造成工程投资的增加。国家“863”课题提出了新型间缝式开口缓冲结构，该缓冲结构改变以前以隧道轴向为主要开口尺寸的开口形式，而是采用开口宽度远大于长度的间缝开口形式，大大减小了缓冲结构的总体长度，提高了缓冲结构的降低效率，继而提高了缓冲结构的经济性。下面对间缝式开口缓冲结构的气动特性进行分析。

1 数值模拟分析

开口型缓冲结构，主要通过优化开口面积，实现将首波压力梯度分解为多个小的次级波释放的目的，开口面积是设计的关键参数之一。提出缓冲结构沿隧道环向开口尺寸远大于隧道轴向开口尺寸的间缝式缓冲结构，对间缝式缓冲结构的气动参数进行数值模拟分析。

1.1 流体数值分析控制方程

流体流动要受到物理守恒定律的支配，这些定律即对应流场控制方程，包括：连续性方程、动量方程和能量方程。如式(1)~式(3)所示[13]。

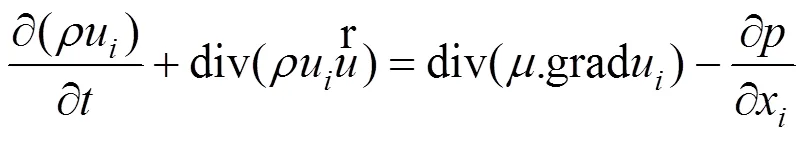
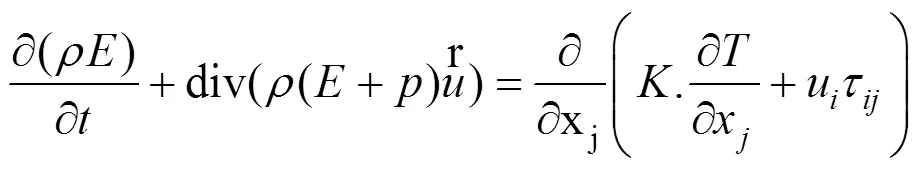
1.2 紊流模型的选取

在流体分析时，紊流模型的选取对计算结果有很大影响，而可选的紊流模式又较多。许多学者在车隧气动分析中，所选取的紊流模型也略有差别，比较常用的有模型[5]及LES模型[14]等。为完善该方法李雪松等[15−16]对大涡模型(LES)开展了一些研究工作。为模拟车体与隧道边界的相对运动，Shin等[17]采用滑移区块法进行了模拟分析。张来平等[18]采用动网格法对非定常流问题进行了分析。本文利用商用工程软件Ansys中的Fluent模块，综合应用动网格和滑移网格法，模拟分析列车进入隧道气动过程，紊流模型选用大涡模型(LES)，计算中介质采用理想气体。

1.3 数值模拟参数

数值模拟中，隧道净空面积T=100 m2，隧道长度=500 m，隧道出入口取300 m，列车启动时刻距离隧道入口100 m。假设传播介质为理想气体，隧道出入口周围边界设置为无限远域(pressure far field)。列车模型采用CRH3型列车，列车截面积S=11.62 m2，隧道阻塞比(=S/T)=0.116，列车速度取=350 km/h。计算中，在隧道内距入口200 m处设置压力监测点，对比压缩波首波压力梯度变化情况，分析缓冲结构缓解微气压波的效果。

隧道及隧道出入口空气域选取如图1所示。间缝式单开口缓冲结构网格划分及结构尺寸标记如图2所示，间缝式双开口缓冲结构网格划分及结构尺寸标记如图3所示。

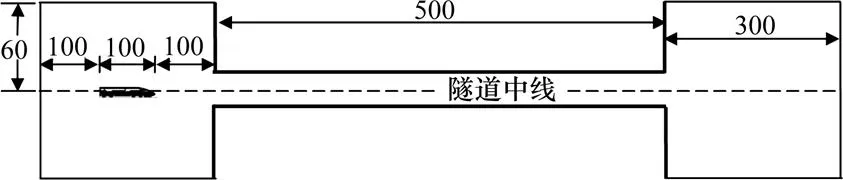
单位：m

图2 单间缝缓冲结构网格划分

影响间缝式缓冲结构气动降低效果的主要因素为开口率和开口距离(开口率=缓冲结构开口面积/隧道横断面面积)，不同开口距离对应不同的开口宽度。计算中间缝式开口环向弧段长度为17.6 m，开口距缓冲结构入口距离=6 m。对于单间缝缓冲结构，通过改变开口纵向长度，研究开口率对缓冲结构降低效果的影响。具体计算工况参数如表1所示。双间缝缓冲结构，保持开口距离=6 m、开口间距=12 m不变，通过改变开口纵向长度参数和来分析开口率对缓冲结构气动降低效果的影响。具体计算工况参数如表2所示。

图3 双间缝缓冲结构网格划分

表1 单间缝缓冲结构数值计算参数

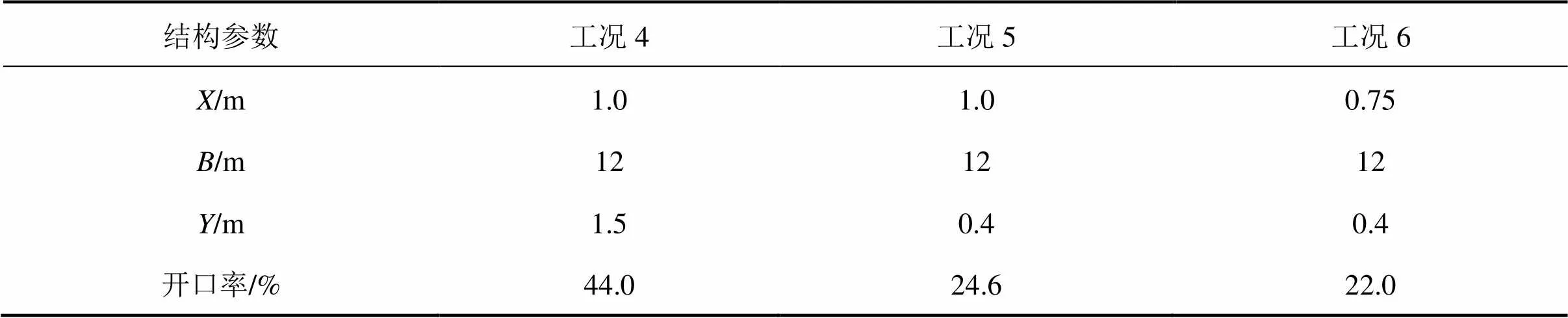
表2 双间缝缓冲结构数值计算参数

1.4 间缝式单开口缓冲结构参数研究

单间缝缓冲结构计算得到的压力梯度曲线如图4所示，具体计算结果如表3所示。

从计算结果可以看出，在开口距离=6 m时：

1) 单间缝缓冲结构的压力梯度曲线显示2个波峰，首波及二次波波峰。

2) 随着开口率的增大，首波压力梯度波峰不断降低，二次波波峰不断上升。

3) 开口长度为1.28 m时(开口率为22.53%)，首波和二次波波峰相等，压力梯度降低率最高。工况2为单间缝缓冲结构的最优形式。

图4 压力梯度曲线

表3 数值模拟计算结果

注：无缓冲结构时，压力梯度曲线为单峰曲线，峰值为13.7 kPa/s

1.5 间缝式双开口缓冲结构参数研究

双间缝缓冲结构各工况计算得到的压力梯度曲线如图5所示，具体计算结果如表4所示。

从计算结果可以看出，在开口距离=6 m，开口间距=12 m时：

1) 双间缝缓冲结构的压力梯度曲线显示出3个波峰，首波及2个次级波波峰。

2) 随着总开口率增大，首波压力梯度波峰不断降低，而次级压力梯度峰值会有所升高。

3) 第一开口宽度为1.0 m，第二开口宽度为0.4 m时，首波和二次波波峰接近，压力梯度降低率最高。工况5为双间缝缓冲结构的最优形式。

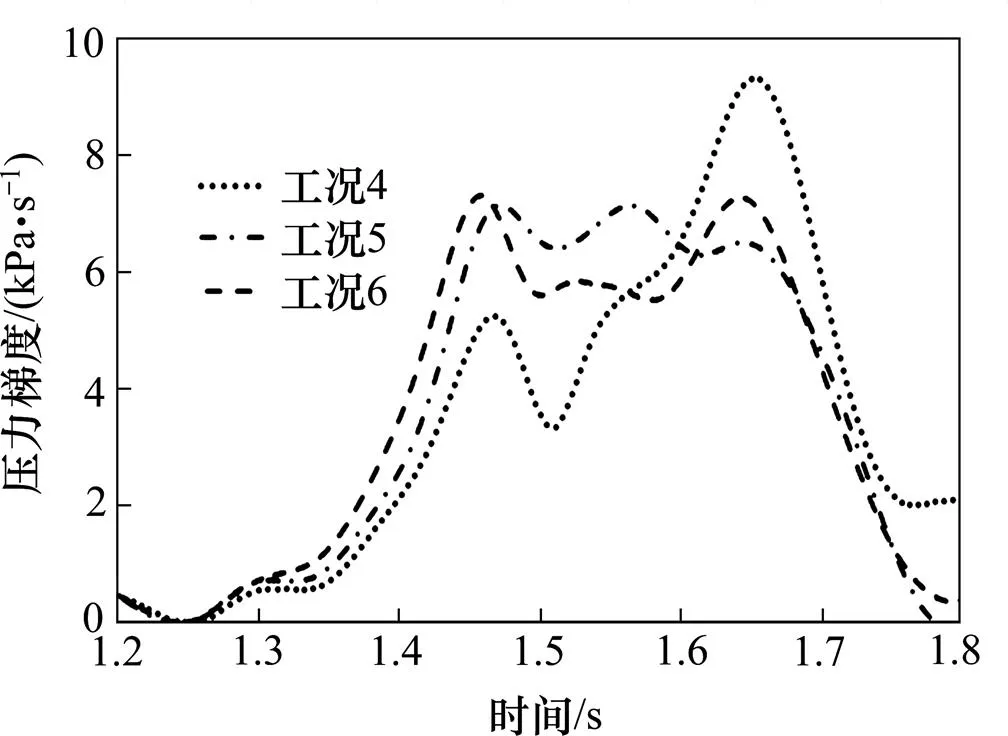
图5 压力梯度曲线

表4 数值模拟计算结果

1.6 间缝式开口缓冲结构与常规顶部开口型缓冲结构对比

由于间缝式开口缓冲结构环向长度远大于纵向长度，使缓冲的长度大大减小，从而提高了缓冲结构的降低效率。下边将间缝式开口缓冲结构与常规顶部开口型缓冲结构进行对比，常规顶部单开口和双开口缓冲结构最优形式如图6和图7所示，具体参数如表5所示。

图6 顶部单开口缓冲结构示意图

综合对比间缝式单开口缓冲结构两种最优工况和顶部单开口缓冲结构的最优工况，其中延米降低率=压力梯度降低率/有效长度，具体情况如表6所示。

从上述对比可以看出：总压力梯度降低率方面，间缝式开口缓冲结构和顶部开口缓冲结构效果相当，但延米降低率，间缝式缓冲结构优势明显，间缝式开口缓冲结构降低效率更高、经济性更好。

图7 顶部双开口缓冲结构示意图

表5 顶部开口型缓冲结构最优工况参数表

注：其中为缓冲结构有效长度，单开口=+，双开口=+++

表6 间缝式开口与顶部开口型缓冲结构对比

2 间缝式双开口缓冲结构模型实验和现场测试

2.1 间缝式缓冲结构模型试验

模型实验采用西南交通大学新建成的滑轨式高速列车气动发射装置。气动压力波发生装置采用以压缩空气为动力的空气炮，将列车模型在炮管内加速到实验需要的速度后发射，列车模型依靠惯性在导轨上滑行通过模型隧道，模拟列车进出隧道的过程，从而实现车隧气动压力波的发生。

模型试验中选取相似比为1/18的列车模型，列车采用轻质铝材加工。隧道模型采用有PC(聚碳酸酯)圆管加工。模型实中列车、隧道的参数选取如表7所示。

2.2 间缝式缓冲结构现场测试

在沪昆客运专线实际工程中应用了间缝式双开口缓冲结构，在联调联试期间对其缓冲效果进行现场测试，洞内压力测点位于距隧道洞口200 m处。

表7 列车实体和模型参数表

2.3 数值计算、模型试验、现场测试结果对比分析

数值计算、模型试验和现场测试3种情况下，最优形式的间缝式双开口缓冲结构压力梯度峰值和速度的关系如图8所示。

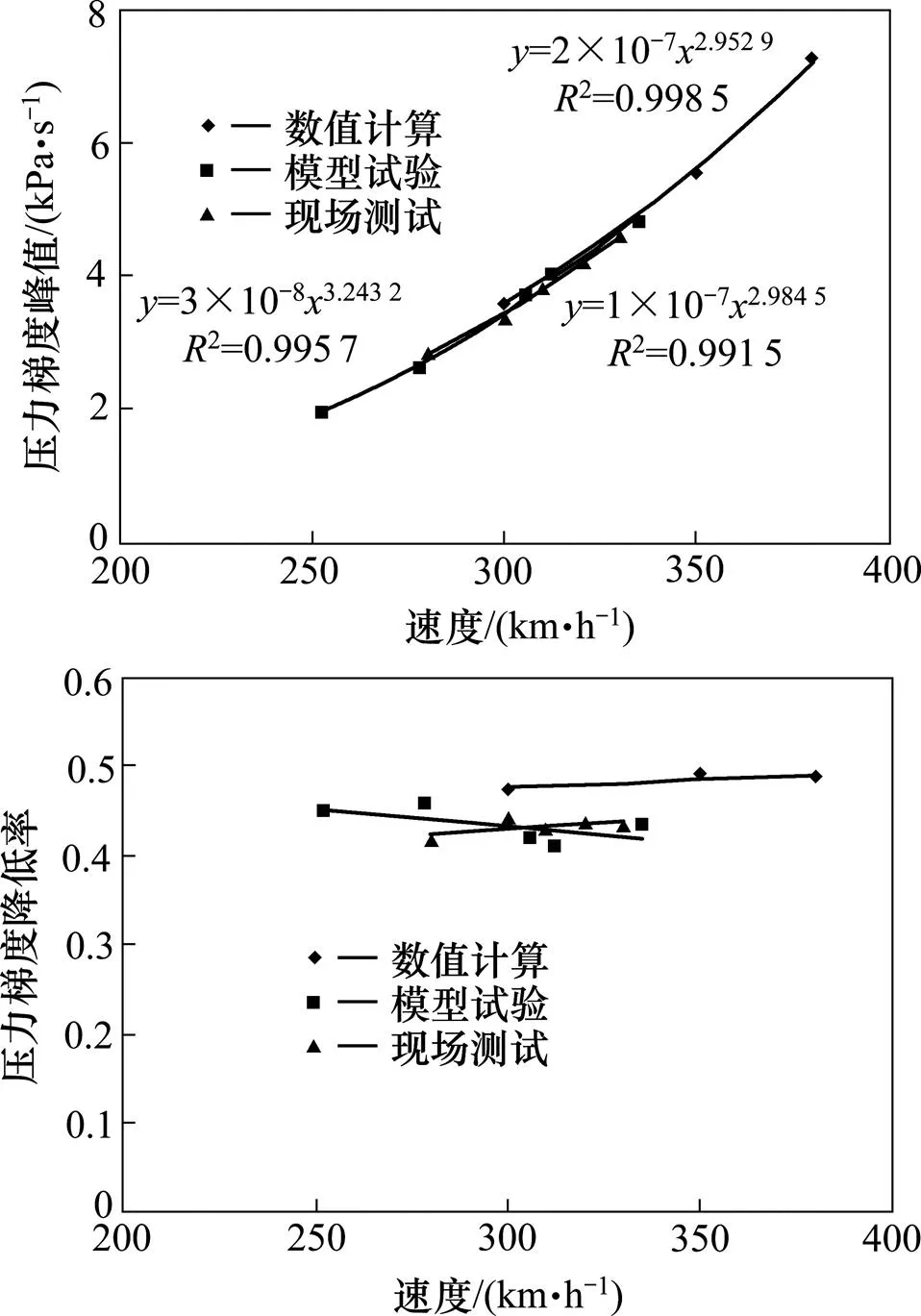
图8 双间缝缓冲结构压力梯度峰值对比

从图8可以看出，现场测试得到的压力梯度峰值曲线和数值计算、模型实验的曲线基本一致。现场测试的压力梯度降低率和模型实验非常接近，略低于数值计算得到的降低率，但相差不大，在误差允许的范围内。

3 结论

1) 列车经过单间缝缓冲结构压力梯度曲线有2个波峰，在开口距离确定的条件下，随着开口率的增大，压力梯度峰值曲线首波波峰不断下降，二次波波峰不断上升。通过分析，确定出优选开口参数，压力梯度降低率达到30%以上。

2) 列车经过双间缝缓冲结构压力梯度曲线有3个波峰，随着总开口率增大，首波压力梯度波峰不断降低，而次级压力梯度峰值会有所升高。通过分析，确定出优选开口参数，压力梯度降低率达到45%以上。

3) 与常规的顶部开口型缓冲结构相比，间缝式缓冲结构延米降低率的优势明显，说明间缝式缓冲结构降低效率更高、经济性更好。

4) 通过模型试验和现场测试，对数值计算结果进行了印证。该新型缓冲结构形式已经应用于工程实际，由于其简便的设计形式，将有很广阔的应用前景。

[1] Raghu S. Raghunathana, Kimb H D, et al. Aerodynamics of high-speed railway train[J]. Progress in Aerospace Sciences, 2002(38): 469−514.

[2] 小沢智. トンネル出口微気圧波の研究[R]. 日本国有铁路铁道技术研究所, 1979.

Ozawa S. Research on micro-pressure ware at the exit of tunnel[R]. Japan’s State-Owned Railway Instute of Railway Technology, 1979.

[3] 骆建军, 高波, 王英学. 高速列车突入隧道与缓冲结构时的数值模拟[J]. 空气动力学报, 2003, 21(3): 376−381.

LUO Jianjun, GAO Bo, WANG Yingxue. Numerical study on tunne-l hood when high-speed train passing a tunnel[J]. Acta Aerodynamica Sinica, 2003, 21(3): 376− 381.

[4] 刘佩斯. 竖井对高速铁路隧道气动效应的影响研究[D]. 成都: 西南交通大学, 2010.

LIU Peisi. Study shaft on the influence to aerodynamic effect of the high-speed railway tunnel[D]. Chengdu: Southwest Jiaotong University, 2010.

[5] 骆建军, 吴尽, 陈鹏飞. 高速铁路并联隧道横通道对隧道内压力变化的影响[J]. 北京交通大学学报, 2015, 39(1): 8−13.

LUO Jianjun, WU Jin, CHEN Pengfei. Pressure change from the cross aisle when the train passing through parallel tunnel of high-speed railway[J]. Journal of Beijing Jiaotong University, 2015, 39(1): 8−13.

[6] 赵文成. 高速铁路隧道缓冲结构的理论和试验研究[D]. 成都: 西南交通大学, 2002.

ZHAO Weicheng. Theoretical and experimental research on the high-speed railway tunnel hood[D]. Chengdu: Southwest Jiaotong University, 2002.

[7] 刘善华. 高速铁路隧道洞口缓冲结构数值模拟及模型试验研究[D]. 成都: 西南交通大学, 2013.

LIU Shanhua. High speed railway tunnel portal buffer structure numerical simulation and model test research[D]. Chengdu: Southwest Jiaotong University, 2013.

[8] Howe M S. Design of a tunnel-entrance hood with multiple windows and variable cross-section[J]. Journal of Fluids and Structures, 2003(17): 1111−1121.

[9] Howe M S. On the design of a tunnel-entrance hood with multiple windows[J]. Journal of Sound and Vibration, 2004(273): 233−248.

[10] Howe M S, The genetically optimized tunnel-entrance hood[J]. Journal of Fluids and Structures, 2007(23): 1231−1250.

[11] LIU Tanghong, TIAN Hongqi, LIANG Xifeng. Design and optimization of tunnel hoods[J]. Tunnelling and Underground Space Technology, 2010(25): 212−219.

[12] WANG Y X, GAO B, WEN Y M, et al. Single opening tunnel hood parameter sensitive research[J]. Applied Mechanics & Materials, 2013(3), 353−356: 1759−1765.

[13] 田红旗. 列车空气动力学[M]. 北京: 中国铁道出版社, 2007.

TIAN Hongqi. Train aerodynamics[M]. Beijing: China Railway Publishing House, 2007.

[14] 马静, 张杰, 杨志刚. 横风下高速列车非定常空气动力特性研究[J]. 铁道学报, 2008, 30(6): 109−114.

MA Jing, ZHANG Jie, YANG Zhigang. Study on the unsteady aerodynamic characteristics of a high-speed train under cross wind[J]. Journal of the China Railway Society, 2008, 30(6): 109−114.

[15] 李雪松. 基于可压缩流方法的大涡模拟及其工程化应用[D]. 北京: 中国科学院研究院, 2006.

LI Xuesong. Large eddy simulation based on the computational method of compressible flows and its application to engineering[D]. Beijing: Chinese Academy of Sciences, 2006.

[16] 张斌. 大涡模拟滤波网格分析及网格自适应控制研究与应用[D]. 上海: 上海交通大学, 2011.

ZHANG Bin. Research and application of filtering grid scale and meshing adaptive-control strategy for large eddy simulation[D]. Shanghai: Shanghai Jiaotong University, 2011.

[17] Shin Chang Hoon, Park Warn Gyu. Numerical study of flow characteristics of the high speed train entering into a tunnel[J]. Mechanics Research Communications, 2003(30): 287−296.

[18] 张来平, 邓小刚, 张涵信. 动网格生成技术及非定常计算方法进展综述[J]. 力学进展, 2010, 40(4): 424−447.

ZHANG Laiping, DENG Xiaogang, ZHANG Hanxin. Reviews of moving grid generation techniques and numerical methods for unsteady flow[J]. Advances in Mechanics, 2010, 40(4): 424−447.

Seam opening tunnel buffer structure aerodynamic characteristic research

WANG Yingxue, CHANG Qiaolei, REN Wenqiang, ZHANG Luoxun

(Key Laboratory of Transportation Tunnel Engineering, Ministry of Education, Southwest Jiaotong University, Chengdu 610031, China)

Using CFD numeral simulation software，the efficiency of new type of tunnel hood, seam opening buffer structure, relieving train-tunnel aerodynamic effect was analyzed in 3-dimension model. The best structure parameter of single and double seam opening tunnel buffer structure was obtained. The calculation results were compared with experiment and field test results. The research results showed that comparing with other kind of hood structures, seam opening buffer structure has higher reduction efficiency of relief pressure gradient and better economy. It is proposed that both total reduction and reduction efficiency should be considered when selecting the form of the buffer structure.

tunnel; buffer structure; seam; pressure gradient; relief efficiency

U451.3

A

1672 − 7029(2018)01 − 0017 − 07

2016−12−01

国家高技术研究发展计划(“863”计划)资助项目(2011AA11A103-3-3-2)

王英学(1972−)，男，吉林东辽人，教授，从事隧道施工力学和车隧空气动力学研究；E−mail：wangyingxue@swjtu.edu.cn