高速铁路牵引回流系统建模分析
2018-01-31魏巍刘炜叶小雯
魏巍,刘炜,叶小雯
高速铁路牵引回流系统建模分析
魏巍,刘炜,叶小雯
(西南交通大学 电气工程学院,四川 成都 610031)
高速铁路牵引回流分布复杂,有必要对其进行精确的建模分析。采用平行多导体传输线理论,搭建统一的牵引网数学模型,实现针对不同空间分布形式的牵引网阻抗和导纳的计算。运用埋地裸导线法对综合地线进行建模,弥补等效接地电阻法不能计算导线电流的缺点,且计及综合地线与其他导线间的耦合,研究不同回流导线中的电流分布比例,并与实测数据进行对比,验证埋地裸导线建模法及牵引网链式网络潮流算法的准确性,并探讨回流测试方案。
综合地线;牵引网;回流系统;链式网络模型
电气化铁路中,牵引回流在各回流导线中的分配比例是研究回流导线选型、牵引网继电保护整定和钢轨电位分析的基础。国内高速铁路采用综合接地系统后,回流比例认知尚不明确。回流系统各导线的回流比例既是前期回流系统设计的重要依据,如钢轨电流的变化是扼流变压器容量配置的参考,也是后期检测线路施工效果的对比依据。牵引网链式网络模型是现在理论和运用比较成熟的1种牵引网仿真模型[1−2]。陈宏伟等[3−5]基于平行多导体传输线理论,将牵引网的组成元件分为纵向串联元件和横向并联元件,可以有效的求解牵引网电压电流分布计算问题。但是,在目前的研究中,当涉及对综合地线的建模时,并没有把综合地线处理成纵向延伸的和其它接触网导线平行的导线,而是将它每隔一定距离等效成一个接地电阻[6−8],这给求取综合地线中的电流带来了困难。高国强等[6−7]指出,接地电阻的大小和地线半径、地线长度、地线形状系数、地线埋设深度、地线与钢轨横向连接线的间距以及土壤电阻率等因素有关。郭晓旭[8]给出了接地电阻的计算式。这几种处理方法的思想是相近的,处理结果在分析钢轨电位的时候是适用的,但是想要运用牵引网链式网络模型来求解综合地线电流就存在困难,因此需要重新对综合地线进行建模。本文在既有研究的基础上,计及综合地线与其它导线间的耦合,运用埋地裸导线法对综合地线重新建模,使之可以方便运用于链式网络模型,更加符合现场实际。在此基础上,本文结合实测数据,验证了综合地线模型的正确性,分析了影响牵引回流比例的因素,探讨了电气化铁路回流比例测试方案。
1 牵引网链式网络模型简介
无论是何种供电方式,不管是单线还是复线,从整体上看,牵引网的骨架都是平行多导体传输线。链式网络模型就是基于多导体传输线理论,将牵引网分为纵向串联元件和横向并联元件,并对这些元件适当建模,得到所需模型,如图1所示[5]。
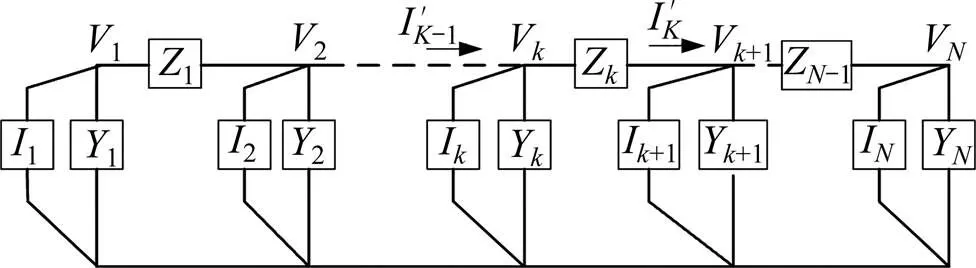
图1 牵引网链式网络模型
设供电臂中导体数为,并将整个供电臂用个切面分割,则图1中的串联阻抗元件Z为2个相邻切面之间的支路阻抗矩阵(×阶),并联导纳元件Y为某切面上各导线之间的导纳矩阵(×阶),I为切面上各导线的注入电流源向量(阶)。对于图1所示链式电路,第节点,有:
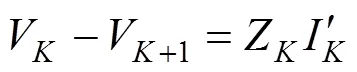
则
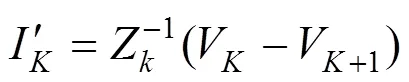
对图1整个链式网络电路可列写式(3)的节点电压方程:
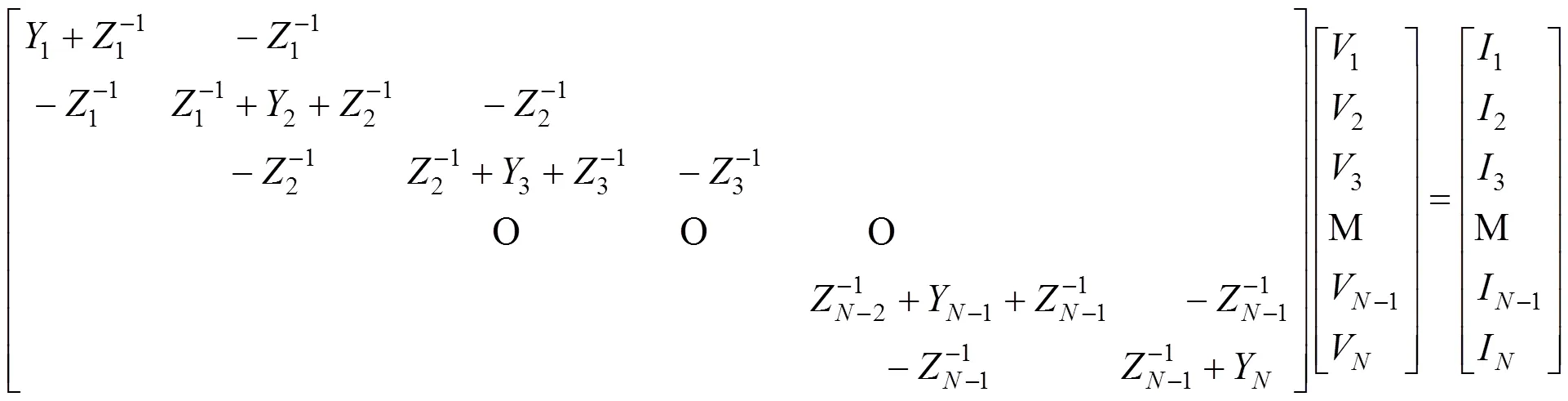
简写为:

则
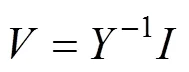
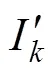
2 综合地线建模
平行多导体传输线理论中所有的计算都是建立在导线单位阻抗矩阵和单位导纳矩阵的基础上的。以往的计算将综合地线等效成了接地电阻,这样的处理实际上是忽略了综合地线和其它接触网导线间的互相影响。若要将综合地线处理成纵向延伸的平行导线,需要得到综合地线单位自阻抗、上下行综合地线之间单位互阻抗、综合地线与其它接触网架空导线单位互阻抗以及整个接触网系统的单位导纳矩阵。
2.1 综合地线单位自阻抗、互阻抗
高速铁路中使用的综合地线具有外护套,为高分子导电塑料护套,具有良好导电性能,且电阻率较低,通常为0.007 Ω∙m,厚度为1~1.2 mm[7]。因此不能采用埋地电缆的相关方法来对其进行建模,本文按埋地裸导线对其进行建模,忽略综合地线外护套对综合地线阻抗的影响。图2是一个平行多导体传输线系统,其中导线和导线为埋地裸导线,导线为架空导线。图2中0为真空磁导率,0为空气介电常数;大地认为是各向同性的,是大地磁导率且»0,为大地介电常数,为大地电阻率。

图2 平行多导体传输线系统
早在1940年,Sunde就解决了埋地裸导线的电气参数计算问题[9]。后来对埋地裸导线的研究基本也都是在其基础上进行的,埋地裸导线电气参数可由一组迭代式描述,如式(6)~(12)所示[10−11]。
导线内阻抗Z为

导线外阻抗Z为
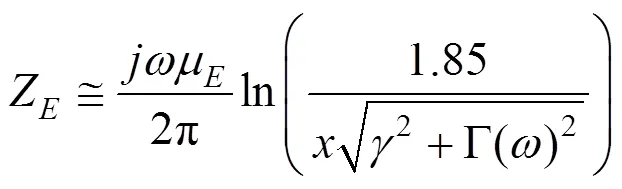
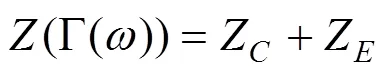

式中:为角频率;为一个与导线位置相关的 参数。

是一个与角频率相关的参数,

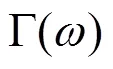
是导线传播常数,
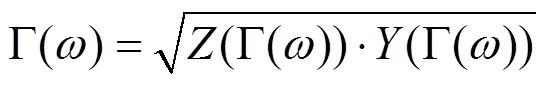
根据以上迭代式(6)~(12),埋地裸导线的自阻抗和泄漏电导可迭代得出。
上下行综合地线间单位互阻抗为式(13)[12]
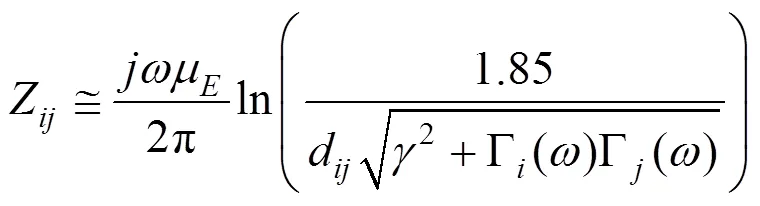
2.2 架空导线和综合地线间单位互阻抗
架空导线和综合地线间互阻抗的计算方法最早可见于CCITT(国际电报电话咨询委员会)1989年出版的关于通信干扰的问题的导则性文件“Directives concerning the protection of telecommunication lines against harmful effects from electric power and electrified railway lines”,文件中给出了互阻抗计算公式(需积分运算)和一定条件下适用的近似,如式(14)所示[13]
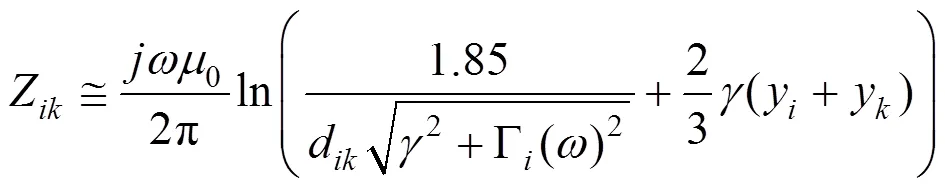
式中:d为导线与导线的间距。
Lucca在上述文件的基础上,进行了进一步的研究,得到了比式(14)更准确的近似公式(15)[13]
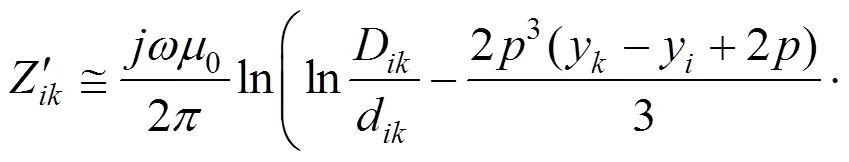
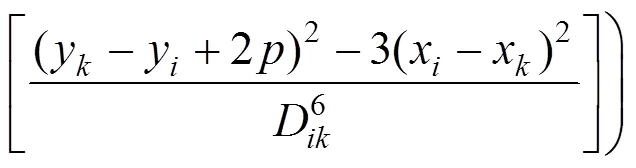
2.3 牵引网系统单位导纳矩阵
牵引网系统的单位电导、电纳参数矩阵可以由导体的电容、电导矩阵和电感矩阵之间的关系得到,但其前提是所有导体处在相同的环境中[14]。为此,假设地面之上和之下的导体处在同一介质中,即空气、大地各向同性且介电常数、电导率和磁导率相同。可求出同一介质中的电容、电导矩阵,如式(16)和(17)[15−16]

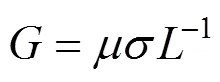
式中:为磁导率;为介电常数;为电导率;为多导体传输线外电感矩阵。
系统单位电纳参数矩阵如式(18)
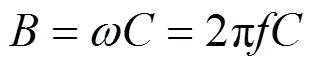
式中:为频率。
对于架空导线,可以忽略架空导线的自电导及互电导耦合[14]。高速铁路高架区段多,一般采用无碴轨道整体道床,钢轨泄漏电阻很大,相应的泄漏电导很小,而上下行钢轨之间、钢轨与综合地线之间的互电导远小于钢轨自电导,因此仅需考虑钢轨自电导[16]。架空导线和钢轨的电导、电纳参数可由式(16)~(18)得出。
对于综合地线,由于土壤介电常数远小于电导率,综合地线间的电纳耦合远小于电导,故可忽略电纳耦合。上下行综合地线之间的互电导可由式(17)得出,其小于自电导,而各地线自电导取值由式(6)得出。对于架空导线、钢轨与综合地线间的电容耦合,其电容值与架空导线、钢轨和大地间的电容值近似相等,可由式(19)计算得出[16]。
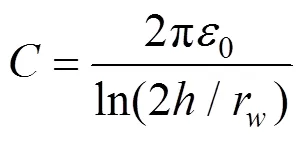
式中:为导体相对地面的高度;r为导体半径。
综上,系统单位导纳矩阵如式(20)所示。
3 案例分析
本文以温福铁路牵引变电所至分区所的回流比例实测案例进行分析。
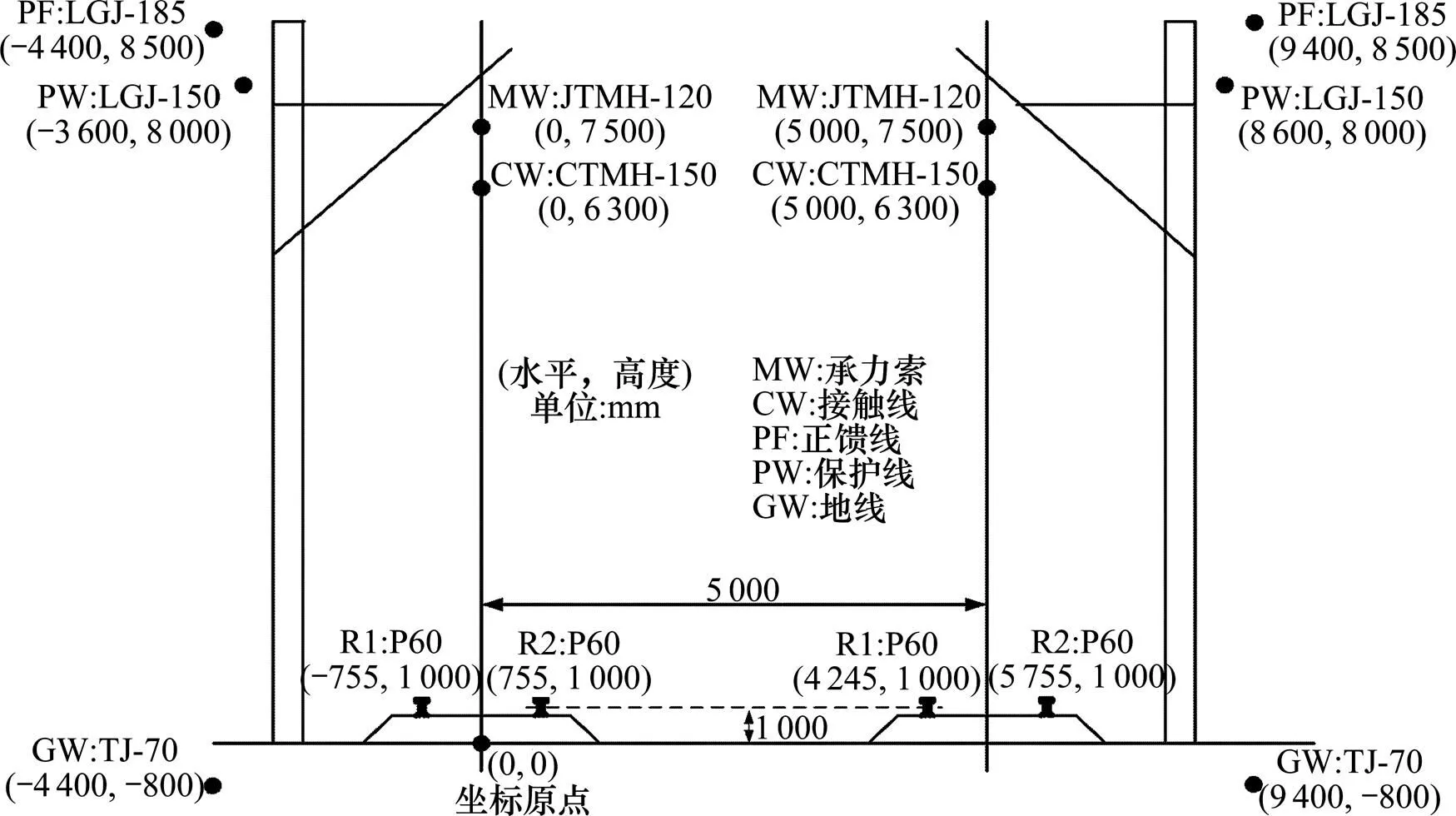
图3 温福铁路AT复线牵引网导线空间分布图
该供电臂长约27.6 km,在16.8 km处AT所和末端分区所处安装自耦变压器,牵引网采用全并联。各参数如下:牵引变电所采用VX接线牵引变压器,所内不设自耦变压器,牵引变压器的额定电压为220/2×27.5 kV,一次侧绕组额定容量为31.5 MVA,二次侧绕组容量为20+20 MVA,阻抗电压百分数为10.5%;电源短路容量为8 000 MVA;AT漏抗为0.45 Ω;变电所和分区所接地网接地阻抗为0.5 Ω;钢轨对地泄漏电阻取100 Ω∙km;PW线绝缘安装;大地电阻率100 Ω∙km;上下行分别设有综合地线GW,每隔1.2 km上下行完全横向连接。牵引网导线型号为:承力索JTMH-120,接触线CTMH- 150,钢轨P60,正馈线LGJ-185,保护线LGJ-150,综合地线TJ-70,综合地线实测电阻为0.27 Ω。图3和图4分别是温福铁路AT复线牵引网导线空间分布图和该供电臂示意图。

图4 温福铁路供电臂示意图
实际测量牵引回流时,测点选在离变电所约3.55 km处。采用电流钳套住2个扼流变压器中心抽头联线,所测得电流值即为钢轨回流。采用电流钳分别套住综合地线、保护线,可分别测得综合地线电流、保护线电流。电流值由录波仪或数采仪 记录。
3.1 牵引回流计算
在该供电臂上行3.48 km处,计算列车取流 1 000 A时牵引回流分布。取牵引变电所为坐标原点,牵引变电所至分区所方向为正方向。
在计算钢轨电位时,本文对综合地线采用了2种处理方法:一种是常用的等效接地电阻法,将它每隔一定距离等效成一个接地电阻[6−8];另一种是本文采用的埋地裸导线法,把综合地线处理成纵向延伸的、和其他接触网导线平行的埋地裸导线。图5是2种地线处理方法下的钢轨电位,其中,1和2分别是上行钢轨电位和下行钢轨电位。
等效接地电阻法最大钢轨电位是39.81 V,本文的埋地裸导线法最大钢轨电位是36.53 V,2种方法的最大计算差别仅3.28 V。因此,就研究钢轨电位来看,本文处理综合地线的方法是可取的,且考虑了综合地线与其它导线的互相影响和横向连结,比直接将综合地线处理成接地电阻更符合实际情况。分别计算出钢轨、保护线和综合地线等回流导线的电流,可以得出牵引回流在每条导线的分布情况。取牵引变电所至分区所方向为回流正方向。图6是全线钢轨电流的分布。1和2分别是上行钢轨电流和下行钢轨电流。可以看出,列车在上行取流后,钢轨回流大部分从上行直接返回牵引变电所,一部分回流通过上下行横向连接线流进了下行钢轨并返回牵引变电所,一小部分的钢轨回流流向了AT所。

图5 钢轨电位
图7是全线保护线电流的分布。3和4分别是上行保护线电流、下行保护线电流。可以得出,在保护线中的牵引回流绝大部分直接通过上行保护线直接返回牵引变电所,一部分通过横向连接线进入下行保护线并流回牵引变电所,另一部分则走向AT所。
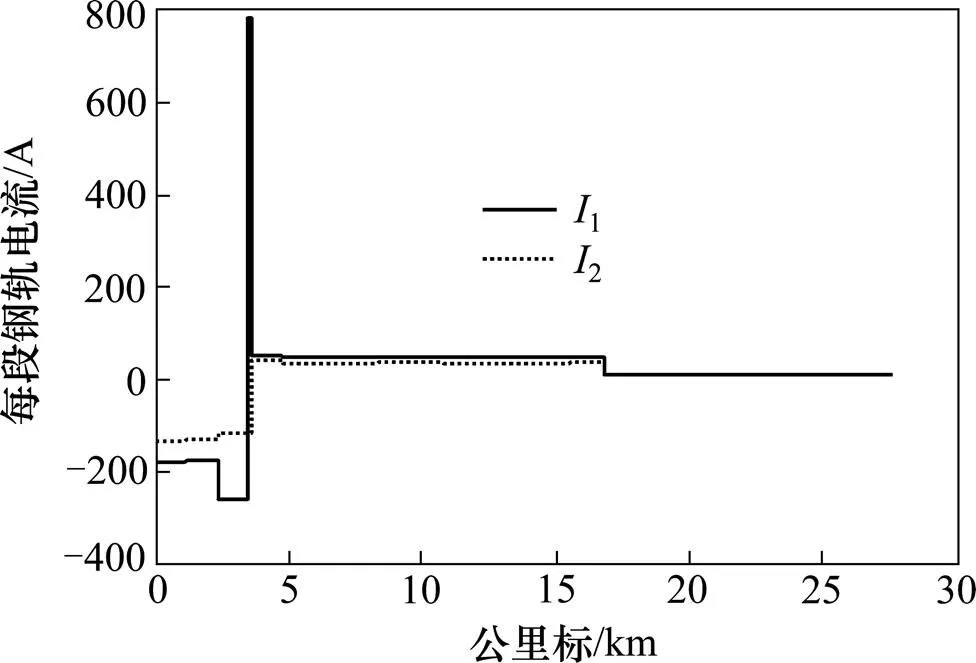
图6 钢轨电流

图7 保护线电流
图8是全线的综合地线电流分布。5和6分别是上行综合地线电流、下行综合地线电流。在综合地线中的牵引回流绝大部分从上行综合地线返回牵引变电所,一部分经过横向连接线流入下行综合地线并返回牵引变电所,一小部分则流向AT所。

图8 综合地线电流
3.2 牵引回流比例分析
将温福铁路测点处的实测回流比例与计算回流比例作对比,如图9所示。
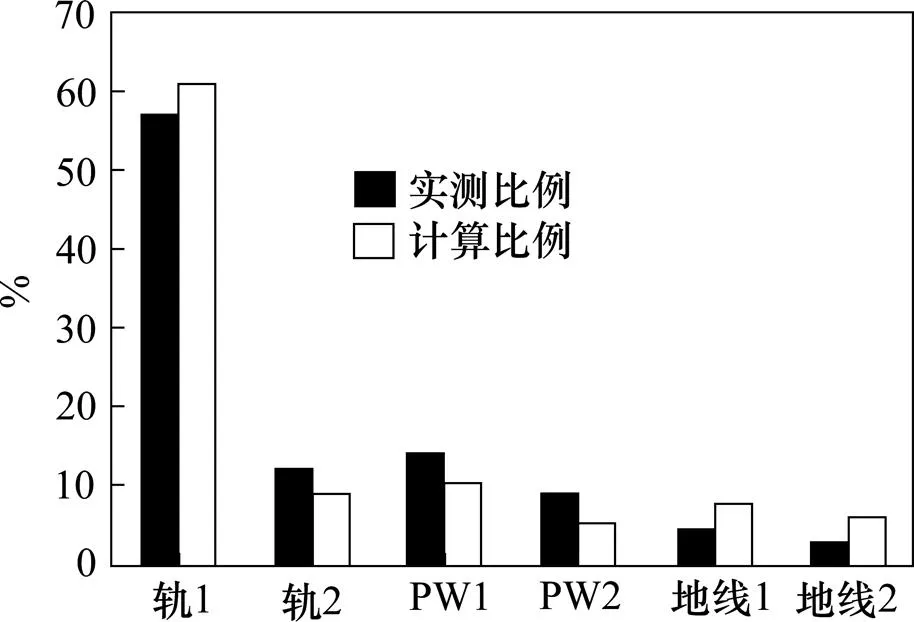
图9 实测比例与计算比例
图9中,轨1、PW1和地线1指的是运行侧各回流导线,对应的轨2、PW2和地线2指的是非运行侧各回流导线。保护线的计算回流比例略低于实测比例,综合地线的计算回流比例略高于实测比例。实际线路上列车数目、位置等运行条件无法精确模拟,供电仿真建模无法将实际线路的全部因素考虑完全,使得计算结果与实测结果出现了一定的误差。可以看到,实测回流比例与计算回流比例两者最大误差为5%,符合得较好。这进一步验证了基于平行多导体传输线理论的链式网络潮流算法以及本文对综合地线建模所采用的埋地裸导线法的准确性。
3.1节仅在一个测点计算了回流分布,为进一步探究列车在不同位置取流时回流的分布情况,分别选取距变电所0.6,3,6.6,12.6,15,16.2,15,16.2,17.4,18.6,21,22.2,24.6,25.8和27 km等位置取流,可以得出列车位于不同位置时全线的回流分布及列车所在处的回流比例。
分析不同取流点的回流分布,可以发现,牵引回流大部分会流向列车最邻近的变电所、AT所或分区所,且列车离所越近,流向该所的回流越大。列车所在回流分区(相邻两横向连接线间的区段)内,由于取流点两边的钢轨回流方向相反,导致此回流分区的部分断面上钢轨回流与保护线、综合地线回流方向相反。
在第1个AT段(0~16.8 km)内,列车位于不同位置时,列车所在处的回流比例如图10所示。
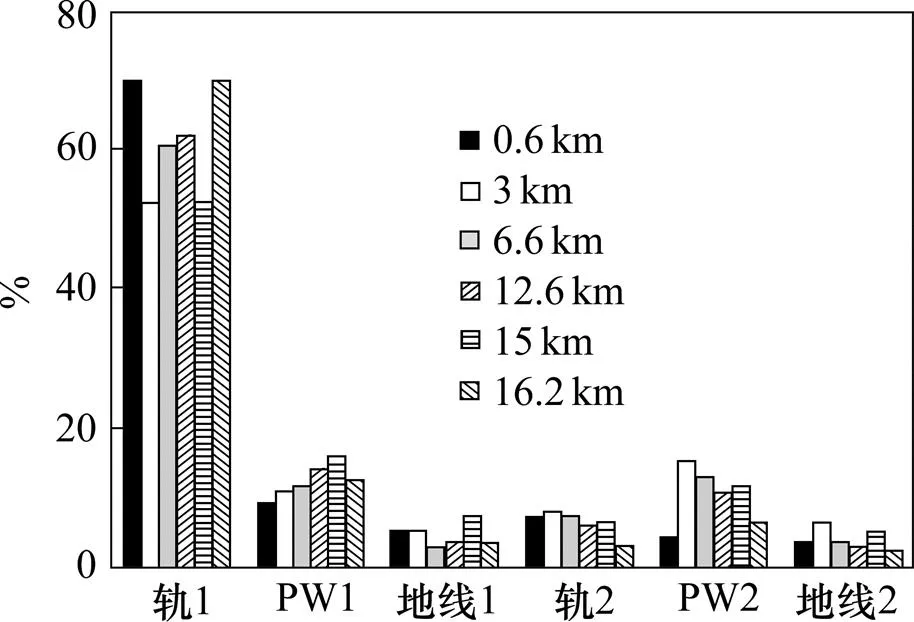
图10 第1个AT段各点回流比例
在第2个AT段(16.8~27.6 km)内,列车位于不同位置时,列车所在处的回流比例如图11所示。

图11 第2个AT段各点回流比例
列车在线路不同位置取流时,回流比例是随位置不同而发生变化的。运行侧钢轨电流比例变化范围51%~74%,PW线电流比例变化范围6%~16%,综合地线电流比例变化范围3%~8%;非运行侧钢轨电流比例变化范围4%~10%,PW线电流比例变化范围4%~15%,综合地线电流比例变化范围2%~7%。总钢轨电流比例变化范围59%~80%,总PW线电流变化范围11%~27%,总综合地线电流变化范围6%~14%。
分析图10和图11可知,当列车在第1个AT区段内靠近变电所或AT所的过程中,运行侧钢轨回流比例变小,相应的其它回流导线回流比例变大,但在十分靠近所(列车和所之间已无横连线)时,越靠近所,运行侧钢轨回流比例越大。
当列车在第2个AT区段内靠近AT所或分区所的过程中,运行侧钢轨回流比例变小,相应的其它回流导线回流比例变大,但在十分靠近所(列车和所之间已无横连线)时,越靠近所,运行侧钢轨回流比例越大。
现有的牵引回流测试方案,通过个别测试点测量列车通过时的回流比例,以此来判断全线回流是否正常。然而,回流系统的回流比例是随注入电流位置不同而发生变化的,现有的回流测试方案存在一定的问题。建议在供电区间上尽可能增加测点数量,各所、区间上多个测点同步测量,以获得更可靠的回流信息。
4 结论
1) 基于平行多导体传输线理论,运用埋地裸导线法对综合地线进行了新的建模,弥补了等效接地电阻法不能计算导线电流的缺点,且计及了综合地线与其它导线间的耦合。供电仿真建模无法将实际线路的全部因素考虑完全,使得计算回流比例与实测比例出现误差。误差不超过5%,进一步验证了埋地裸导线法的可行性和准确性。
2) 选取一段典型的含综合地线的实测线路进行了建模仿真,研究了列车在不同位置取流时回流的分布情况。研究表明,牵引回流大部分会流向列车最邻近的所,且列车离所越近,流向该所的回流越大,列车所在回流分区的部分断面上钢轨回流与保护线、综合地线回流方向相反。
3) 研究了列车在不同位置取流时列车所在处的回流比例情况。研究表明,列车在线路不同位置取流时,列车所在处的回流比例是随位置不同而发生变化的。现场测试只能选在某些固定点测试,仅通过个别点获取回流信息并不完善。建议在全供电区间进行多个测点同步测试。
4) 上、下行PW线,上、下行综合地线之间的回流基本均匀。PW线回流比例为11%~27%之间,综合地线回流比例为6%~14%之间。综合地线回流是PW线回流的一半左右。计算回流比例大小及其变化范围为回流系统的设计和检测提供了参考数据,具有重要意义。
[1] 张俊骐, 吴命利. 电气化铁路牵引网节点方程组数值解法比较[J]. 电工技术学报, 2016, 31(15): 109−116.
ZHANG Junqi, WU Mingli. Comparison of numerical methods for nodal analysis in electric railway traction network[J]. Transactions of China Electrotechnical Society, 2016, 31(15): 109−116.
[2] Hanmin Lee, Changmu Lee, Gilsoo Jang. Harmonic analysis of Korean high-speed railway using the eight-port representation model[J]. IEEE Transactions on Power Delivery, 2006, 21(2): 979−986.
[3] 陈宏伟, 耿光超, 江全元. 电气化铁路牵引供电系统车网耦合的潮流计算方法[J]. 电力系统自动化, 2012, 36(3): 76−80, 110.
CHEN Hongwei, GENG Guangchao, JIANG Quanyuan. Power flow algorithm for traction power supply system of electric railway based on locomotive and network coupling[J]. Automation of Electric Power Systems, 2012, 36(3): 76−80, 110.
[4] 胡海涛, 何正友, 王江峰, 等. 基于车网耦合的高速铁路牵引网潮流计算[J]. 中国电机工程学报, 2012, 32(19): 101−108, 192.
HU Haitao, HE Zhengyou, WANG Jiangfeng, et al. Power flow calculation of high-speed railway traction network based on train-network coupling systems[J]. Proceedings of the CSEE, 2012, 32(19): 101−108, 192.
[5] 王越. 牵引供电系统负荷过程的建模与计算机仿真研究[D]. 北京: 北京交通大学, 2015.
WANG Yue. Research on modeling and computer simulation of traction power supply system’s load process[D]. Beijing: Beijing Jiaotong University, 2015.
[6] 高国强, 董安平, 张雪原, 等. 高速铁路综合地线的接地效果[J]. 西南交通大学学报, 2011, 46(1): 103−108.
GAO Guoqiang, DONG Anping, ZHANG Xueyuan, et al. Grounding effect of integrated grounding wire for high-speed railway[J]. Journal of Southwest Jiaotong University, 2011, 46(1): 103−108.
[7] 马九洋, 张晨, 范季陶. 高速铁路贯通地线地电位分布及影响因素分析[J]. 电波科学学报, 2010, 25(增): 131− 136.
MA Jiuyang, ZHANG Chen, FAN Jitao. Analysis of high-speed railway ground potential distribution and influence factors[J]. Chinese Journal of Radio Science, 2010, 25(Suppl): 131−136.
[8] 郭晓旭. 高速铁路牵引网建模与仿真[D]. 成都: 西南交通大学, 2014.
GUO Xiaoxu. Modeling and simulation of traction network of high-speed railway[D]. Chengdu: Southwest Jiaotong University, 2014.
[9] Sunde E D. Surge characteristics of a buried bare wire[J]. Electrical Engineers, 1940, 59(12): 987−991.
[10] Hideki Motoyama. Electromagnetic transient response of buried bare wire and ground grid[J]. IEEE Transactions on Power Delivery, 2007, 22(3): 1673−1679.
[11] Hideki Motoyama. Experimental and analytical studies on lightning surge characteristics of a buried bare wire[J]. Electrical Engineering in Japan, 2008, 164(3): 35−41.
[12] 潘睿. 合宁客运专线综合接地性能测试研究[D]. 北京:北京交通大学, 2009.
PAN Rui. Test and research on the performance of the integrated grounding system of he-ning passenger dedicated railway[D]. Beijing: Beijing Jiaotong University, 2009.
[13] Lucca G. Mutual impedance between an overhead and a buried line with earth return[C]// Ninth International Conference on Electromagnetic Compatibility. Manchester: IEEE, 1994: 80−86.
[14] Hill R J, CEVIK I H. On-line simulation of autotransformer-fer AC electric railroad traction networks[J]. IEEE Transactions on Vehicular Technology, 1993, 42(3): 365−372.
[15] 米泽辉. AT供电系统轨地电位与降低措施研究[D]. 成都: 西南交通大学, 2013.
MI Zehui. Study on rail potential and reducing measures of at-fed traction power system[D]. Chengdu: Southwest Jiaotong University, 2013.
[16] 马庆安. 高速铁路AT供电若干问题的研究[D]. 成都:西南交通大学, 2013.
MA Qingan. Study on some problems of traction power supply systems in high-speed railway[D]. Chengdu: Southwest Jiaotong University, 2013.
Modeling analysis of high speed railway traction return current system
WEI Wei, LIU Wei, YE Xiaowen
(School of Electrical Engineering, Southwest Jiaotong University, Chengdu 610031, China)
The distribution of high speed railway traction return current is complex. It is necessary to carry out its accurate analysis of the model. Based on the parallel multi-conductor transmission line theory, this paper sets up a unified mathematical model of the traction network and realizes the impedance calculation for different forms of traction network. With the method of buried bare wires, the modeling of integrated grounding wire makes up for the shortcomings of grounding resistance equivalent method which cannot calculate wire current, and takes the coupling between the integrated grounding wire and the other wire into account. The distribution proportion of current in different return wires is figured out and compared with the measured return current ratio. In this way, the accuracy of the buried bare wires method and the chain network flow algorithm are verified. The return current test schemes are explored.
integrated grounding wire; traction network; return current system; chain network model
U223.2
A
1672 − 7029(2018)01 − 0031 − 08
2016−12−11
中国铁路总公司科技研究开发计划资助项目(2014J009-B)
刘炜(1982−),男,湖南益阳人,副教授,博士,从事牵引供电系统理论、计算机仿真、电能质量研究;E−mail:liuwei_8208@swjtu.cn
