基于偏好信息的高速铁路车站选址研究
2018-01-31王睿李延来朱江洪
王睿,李延来, 2,朱江洪
基于偏好信息的高速铁路车站选址研究
王睿1,李延来1, 2,朱江洪1
(1. 西南交通大学 交通运输与物流学院,四川 成都 610031;2. 西南交通大学 综合交通运输智能化国家地方联合工程实验室,四川 成都 610031)
为研究高速铁路(以下简称“高铁”)车站选址方案评价的多属性决策问题,从经济因素、路网因素、功能因素、协调因素和环境因素等5个方面构建评价指标体系。针对已有研究评估信息表征不完整和集结不准确等不足,提出1种直觉乘法偏好信息下的高铁车站选址方案评价方法。该方法运用直觉乘法数表征方案偏好评估信息,结合偏好信息隶属度和非隶属度交叉影响下的直觉乘法数运算规则,提出直觉乘法交叉加权平均(IMIWA)算子和广义直觉乘法交叉加权平均(GIMIWA)算子与其相关性质,然后利用GIMIWA算子对高铁车站选址备选方案的偏好信息进行集结并确定最终方案排序。算例结果证实所提出方法的可行性和有效性。
高速铁路车站;选址方案评价;直觉乘法偏好信息;广义直觉乘法交叉加权平均(GIMIWA)算子
自秦沈客运专线开通运营以来,十几年既有铁路高速化改造以及高铁建设使我国拥有了全世界规模最大以及运营速度最快的高速铁路网[1]。其中,沿线高铁车站是铁路与出行民众直接对话的窗口,故其选址研究一直是高铁建设的重要环节。车站选址方法主要有建模优化和方案比选2种,其中建模优化方法旨在通过选取车站选址优化目标函数和相关约束条件,构建优化模型求得车站站位;方案比选方法为结合车站选址指标确定若干备选方案,再利用相关评判方法确定最优方案。在实际高铁车站规划问题中,由于城市用地局限性较大,可用于建设高铁车站的站位有限,使得建模优化方法往往难以发挥其应有效用,此时采用方案比选方法更为适合。目前,国内外学者在铁路车站选址方案评价研究领域已成果显著,为刻画评估信息的不确定性以及集结评估信息,模糊集理论[2]和多属性决策方法被广泛运用到相关研究之中。Smith[3]通过将语义评估信息转化为三角模糊数,对悉尼市郊铁路沿线车站选址方案进行模糊综合评价;XI等[4]根据铁路车站实际情况,构建了基于熵值的灰色关联分析模型,并对城际铁路车站选址方案进行评价;廖勇[5]同样利用可转化为三角模糊数的语言变量表征评估信息,结合逼进理想解的排序(TOPSIS)方法求解铁路客运站选址方案综合评价指数并对其排序;罗昊等[6]运用了指向图和Kemeny社会选择函数相结合的群决策方法对客运站选址方案进行排序;罗霞等[7]结合了客运站选址评价指标,引入改进属性层次模型(AHM)对方案进行比选;朱晓宁等[8]构建了基于熵权法的TOPSIS模型,并对城际铁路客运站选址方案进行排序。然而,上述研究评估信息载体大多局限于实数和三角模糊数,在刻画评估信息不确定性上还有待深入研究。自Zadeh[2]和Atanassov[9]相继提出模糊集和直觉模糊集理论以来,以这2种模糊概念作为属性评估值运用到偏好信息下多属性决策问题之中的研究屡见不鲜[10−12]。传统模糊偏好信息使用互补型0.1-0.9标度进行赋值[13],并认为等级之间分布均匀,这与部分实际情况(例如经济学中的边际效用递减率)相违背。XIA等[14]利用互反型1-9标度对偏好信息进行赋值,提出了直觉乘法集和直觉乘法偏好关系的概念,其可同时表征决策者对于不同方案间的偏好信息的隶属度和非隶属度,更准确的体现了偏好信息的不确定性,使决策结果更贴近实际情况。此后,众多学者对直觉乘法和区间直觉乘法集成算子进行了广泛研究[15−17],但是都是基于传统直觉乘法数运算规则所提出。HE等[18]考虑隶属度信息和非隶属度信息的交叉影响,提出了改进的直觉模糊数运算规则,Garg[19]将此思想运用到直觉乘法集之中,提出了偏好信息隶属度和非隶属度交叉影响下的直觉乘法数运算规则和相应几何加权算子。目前,直觉乘法交叉集成算子的相关研究较为缺乏,同时尚未出现直觉乘法偏好信息背景下铁路车站选址的相关研究。综上所述,针对既有研究存在的空白和不足,本文提出了一种基于广义直觉乘法交叉加权平均(GIMIWA)算子的高铁车站选址方案评价方法。首先,通过系统性分析,从经济因素、路网因素、功能因素、协调因素和环境因素等5个方面构建了高铁车站选址方案评价指标体系;其次,结合偏好信息隶属度和非隶属度交叉影响下的直觉乘法数运算规则提出了直觉乘法交叉加权平均(IMIWA)算子和GIMIWA算子,并指出其具备的相关性质;再次,通过GIMIWA算子对不同高铁车站选址备选方案的直觉乘法数形式的偏好信息进行集结,并利用记分函数值和精确函数值确定方案排序;最后,将该方法应用于高铁车站选址方案评价算例之中,证实其有效性和可行性并讨论了不同值对于结果的影响。
1 高铁车站选址方案评价指标体系
高铁车站选址方案评价指标的选取直接影响到备选方案排序结果,其本身也是一项系统工程,因此必须建立在实际情况基础上,遵循全面性、层次性和针对性等原则构建高铁车站选址方案评价指标体系,为决策者全面准确地表达偏好信息做出铺垫。本文将选取经济因素、路网因素、功能因素、协调因素和环境因素等5个方面对高铁车站选址方案进行综合评判。
1.1 经济因素
高铁车站主要经济投入包括前期基础设施建设费用和日常运营费用等,不同的备选方案的费用预算各有不同。此外,既有高铁车站多数已经成为所在城市的地标性建筑,大量的客流集散给车站周边带来商机,因此,建成后的车站市场吸引力大小也是选址方案的重要评价指标;同时,高铁车站站位的不同也会在不同程度上带动当地经济的发展。
1.2 路网因素
建设高铁车站的目的之一是方便旅客出行,缓解路网旅客运输压力,因此,车站站位应尽可能设置在路网规划区域内人口密集区域或旅客运输集中的节点上。同时,车站站位确定后所形成的路网利用率、供需平衡和鲁棒性等能力的大小也是影响选址因素之一。此外,高铁车站选址需要考虑国家重点项目、国家政策和地方政策、政治需求、当地居民出行需求和国防等因素,在服务人们出行的同时尽量达到国家整体对于高铁路网的发展要求。
1.3 功能因素
高铁车站站位决定了车站主体设计、布置和规模,由此确定的旅客发送能力是方案选取的重要影响因素。在开通运营后,确保旅客安全是日常工作的重中之重,站位所决定的车站突发应急能力直接影响到日后运营情况。此外,还需保留车站未来扩建改造的可能性,扩建改造条件影响到高铁车站整体功能。
1.4 协调因素
高铁建设与城市规划存在一定的矛盾关系,若车站与市区距离较远,会造成旅客出行不便,增加市内交通压力;若车站与市区距离太近,会对城市发展造成不利影响,因此,车站站位需要尽可能同时满足近期协调和远期发展的要求,而与城市交通的协调性同样重要。同时,高铁车站建成后与枢纽内其他铁路车站的分工和衔接也是选址的评价 因素。
1.5 环境因素
随着国家经济发展和人们生活水平提高,环境问题越来越受到国家重视,备选方案在环境因素的表现同样重要。一方面选址地生态环境直接影响到方案的选择;另一方面车站建设和运营过程中会对当地大气、水源等自然环境造成影响,故需要综合考虑2方面影响。而高铁车站运营后,列车高速运行中会产生噪声和辐射,对沿线居民的正常生活造成影响的大小也是评价因素之一。
综上所述,构建高铁车站选址方案决策评价指标体系,如图1所示。可以看出高铁车站选址问题实质上为一类多目标优化问题,通过建模优化方法难以解决,宜利用多属性决策相关方法对备选方案进行比选。
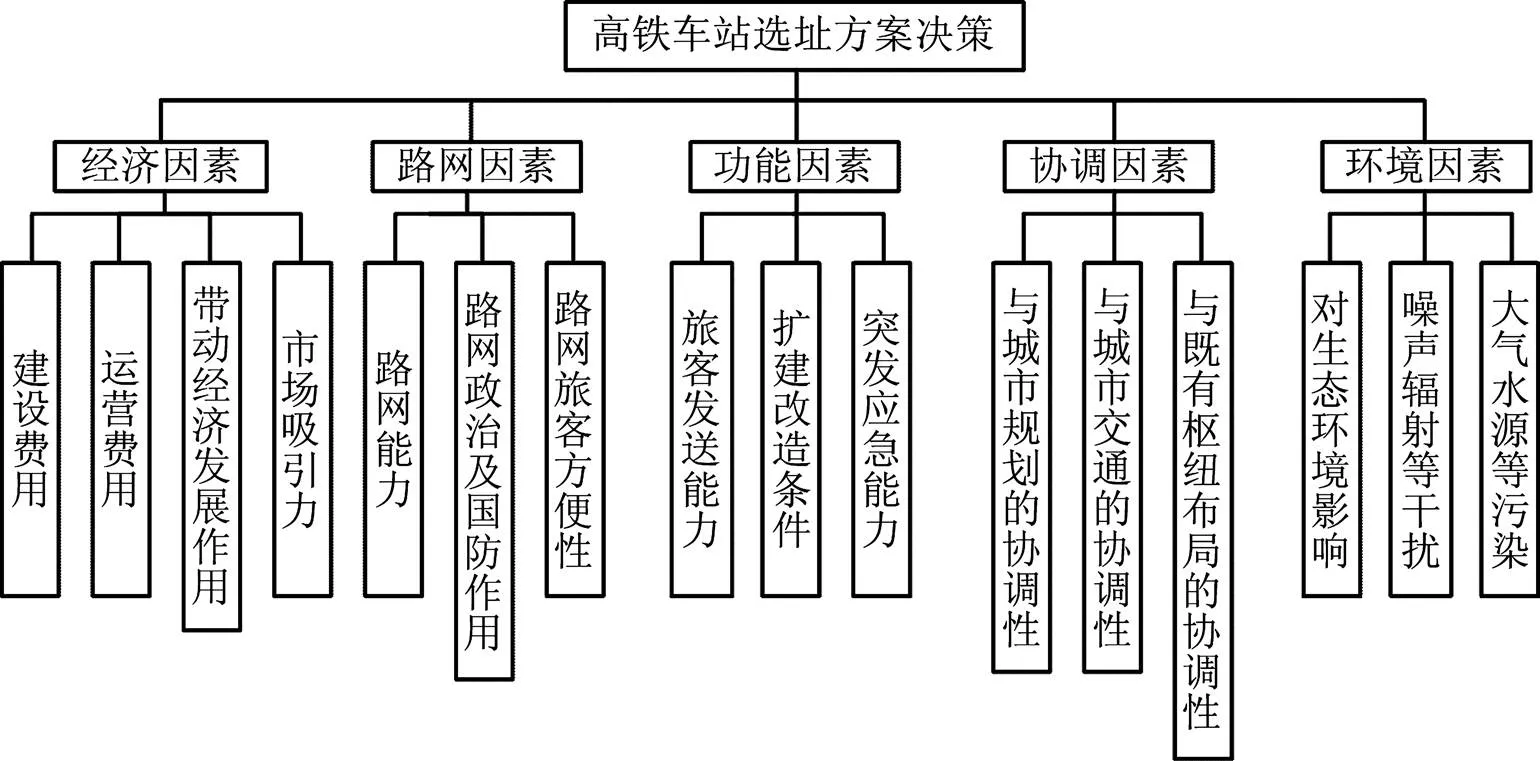
图1 高铁车站选址方案决策评价指标体系
2 相关概念
XIA等[14]将互反型1-9标度赋值的偏好信息概念引入直觉偏好关系之中,提出了直觉乘法偏好关系,将直觉乘法数构成的直觉乘法集作为评估信息的载体。直觉乘法数既保持了直觉偏好信息能够同时表征隶属度和非隶属度的特点,又改进了原有互补型0.1-0.9标度赋值等级均匀与实际不符的不足,一经提出便被广泛应用于多属性决策问题之中,表征具有不确定性的偏好信息。

为后续研究方便,将直觉乘法数简写为(,)。其中,假设为决策者在比较方案和方案关于某评价指标对于方案偏好评价的直觉乘法数,和分别为决策者对方案和方案的偏好程度,取值按照互反型1-9标度确定,见表1,介于表中语义信息之间的偏好评价可由对应标度之间任意量值表示,充分表达评价信息的不确定性,而与语义信息相反的描述所对应量值为相对量值的倒数形式。

表1 1-9标度语义信息
定义2[14]设=(,)为一个直觉乘法数,则其记分函数和精确函数分别为

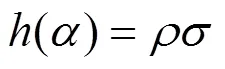
依据直觉乘法数的记分函数和精确函数,文献[14]提出直觉乘法数比较的评判方法。
定义3 设1和2为2个直觉乘法数,则:
此后,文献[14]还定义了直觉乘法数的运算规则,但其并未考虑隶属度信息和非隶属度信息的交叉影响,这对信息集结所得结果准确性会造成一定影响。Garg[19]结合文献[18]中的思想,提出了偏好信息交叉影响下的直觉乘法数运算规则。
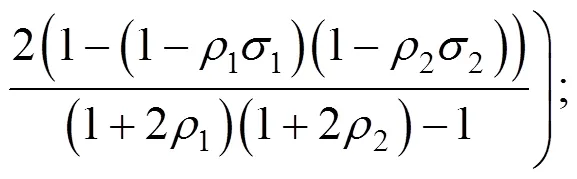
根据定义4易证下述定理,表明交叉影响下直觉乘法数运算规则的合理性。

3 直觉乘法交叉集成算子
集成算子作为模糊评估信息融合的工具,一直以来是国内外学者的研究热点,其对应模型根据模糊评估信息的种类不同而不同。文献[14−17]提出了直觉乘法加权平均(IMWA)算子、直觉乘法加权几何(IMWG)算子和其他集成算子,但其忽略了信息融合时隶属度和非隶属度信息的交叉影响,造成信息的丢失。本节将结合定义4构建全新的直觉乘法交叉集成算子,并提出基于直觉乘法交叉集成算子的决策方法。
3.1 直觉乘法交叉加权平均算子
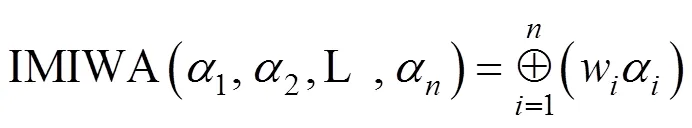

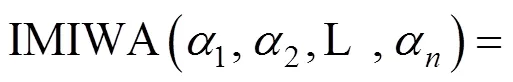

定理2易由数学归纳法证明,在此省略。此外,由定义4中直觉乘法数的运算法则和定理1可得IMIWA算子具备以下性质。
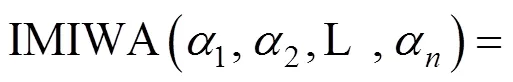
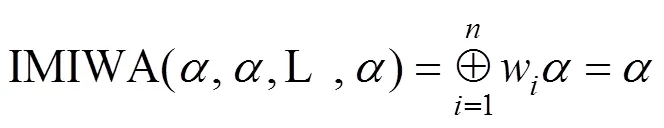
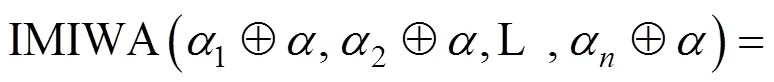

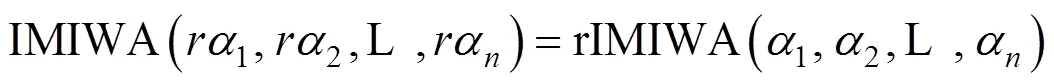


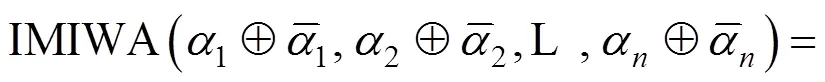

3.2 广义直觉乘法交叉加权平均算子
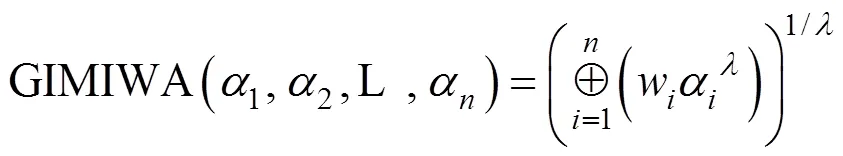
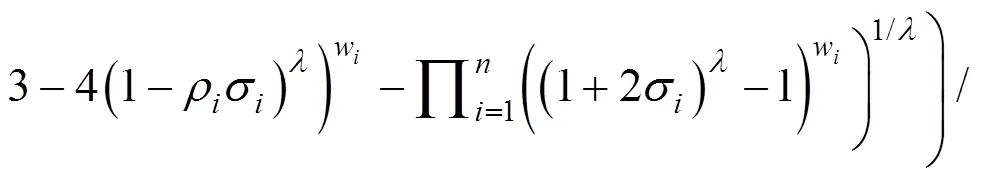

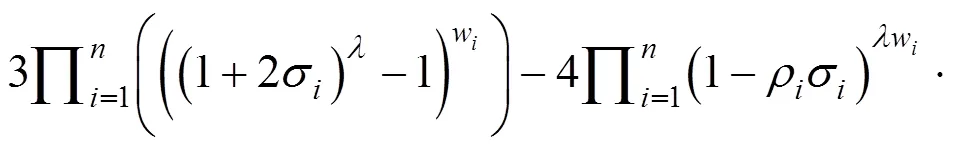
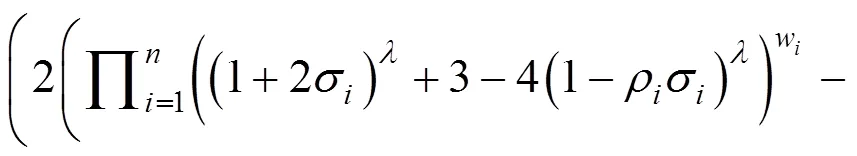

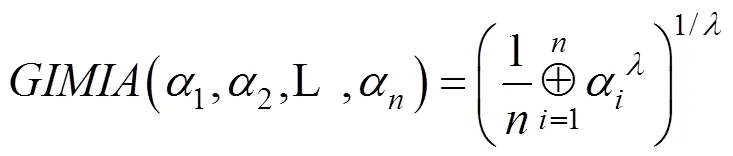
3.3 基于GIMIWA算子的决策方法
4 算例分析


表2 经济因素直觉乘法判断矩阵

表3 路网因素直觉乘法判断矩阵
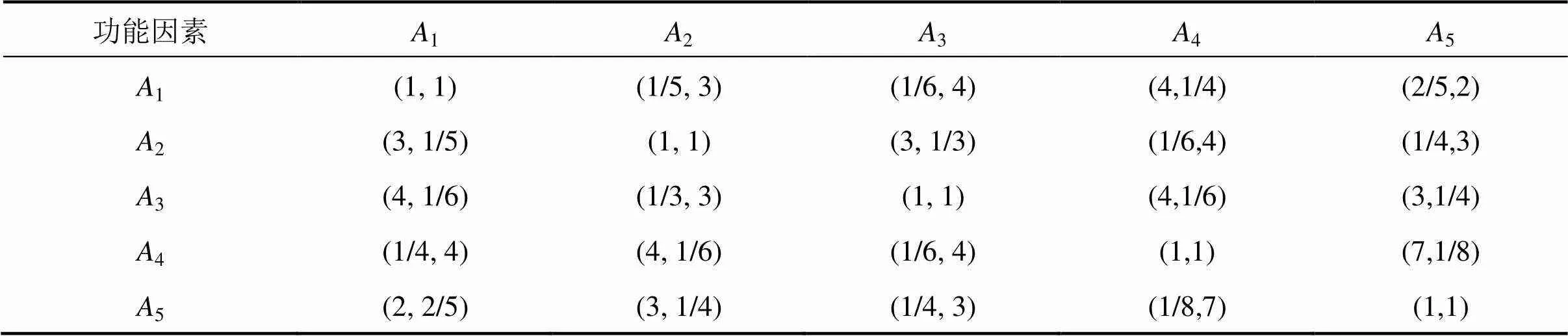
表4 功能因素直觉乘法判断矩阵

表5 协调因素直觉乘法判断矩阵
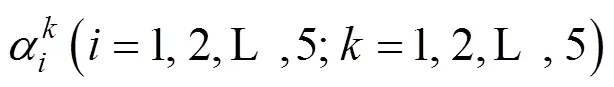

表6 环境因素直觉乘法判断矩阵
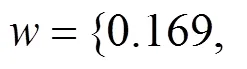

表7 综合直觉乘法数

表8 综合直觉乘法数记分函数值
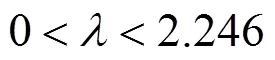

图2 GIMIWA算子下方案记分函数值
5 结论
1) 针对我国高铁选址决策问题,提出一种直觉乘法偏好信息下基于GIMIWA算子的高铁车站选址方案评价方法,构建高铁车站选址方案评价指标体系,利用语义信息转化的直觉乘法数表征专家对于不同方案在不同指标下偏好的评估信息,较三角模糊数更有效刻画了车站选址决策中评估信息的不确定性,更贴近实际情况。
2)考虑偏好信息隶属度和非隶属度交叉影响,提出IMIWA算子和GIMIWA算子并证明其满足的相关性质,在直觉乘法交叉集成算子方面进行了拓展研究,并运用GIMIWA算子集结评估信息,在信息集结上较已有直觉乘法集成算子更为准确,且运算过程较TOPSIS、AHP等多属性决策方法更为 简便。
3) 在构建的高铁车站选址方案评价指标体系基础上,结合算例从经济因素、路网因素、功能因素、协调因素和环境因素对5个高铁车站选址备选方案进行排序,证实该方法有效可行,并通过调整算子中值分析其对结果的影响,在实际决策中可根据专家态度确定值大小。
4) 高铁车站选址方案评价指标之间相互影响,未来的研究方向为考虑不同评价指标之间相互影响下,构建相应Choquet算子对高铁车站选址方案进行比选。
[1] 杨修昌, 戴弘. 高速铁路客运[M]. 北京: 中国铁道出版社, 2012: 1−5.
YANG Xiuchang, DAI Hong. High-speed railway passenger transportation[M]. Beijing: China Railway Publishing House, 2012: 1−5.
[2] Zadeh L A. Fuzzy sets[J]. Information & Control, 1965, 8(65): 338−353.
[3] Smith P N. Fuzzy evaluation of potential suburban railway station locations[J]. Journal of Advanced Transportation, 1993, 27(2): 153−179.
[4] XI Jiangyue, ZHU Xiaoning. Study on location selection of the intercity railway passenger station based on fuzzy entropy-based grey correlation analysis[J]. Applied Mechanics & Materials, 2013, 336−338(14): 2508−2511.
[5] 廖勇. 基于三角模糊数的铁路客运站选址方案评价方法[J]. 中国铁道科学, 2009, 30(6): 119−125.
LIAO Yong. Evaluation method for the location selection of railway passenger station based on triangular fuzzy number[J]. China Railway Science, 2009, 30(6): 119−125.
[6] 罗昊, 何世伟. 群决策方法在铁路枢纽客运站选址方案比选中的应用[J]. 铁道运输与经济, 2010, 32(6): 75−78.
LUO Hao, HE Shiwei. Application of group decision-making method on the location plan comparison and selection of railway hub passenger stations[J]. Railway Transport and Economy, 2010, 32(6): 75−78.
[7] 罗霞, 廖勇. 基于改进 AHM 模型的铁路客运站选址研究[J]. 铁道工程学报, 2012, 29(1): 73−77.
LUO Xia, LIAO Yong. Research on the AHM model for location selection of railway passenger station[J]. Journal of Railway Engineering Society, 2012, 29(1): 73−77.
[8] 朱晓宁, 席江月. 基于熵权-TOPSIS的城际铁路客运站选址研究[J]. 铁道运输与经济, 2013, 35(10): 32−36.
ZHU Xiaoning, XI Jiangyue. Study on location of intercity passenger station based on entropy weighting-TOPSIS[J]. Railway Transport and Economy, 2013, 35(10): 32−36.
[9] Atanassov K T. Intuitionistic fuzzy sets[J]. Fuzzy Sets & Systems, 1986, 20(1): 87−96.
[10] XU Zeshui. Intuitionistic preference relations and their application in group decision making[J]. Information Sciences, 2007, 177(11): 2363−2379.
[11] 徐泽水. 直觉模糊偏好信息下的多属性决策途径[J]. 系统工程理论与实践, 2007, 11(11): 62−71.
XU Zeshui. Approaches to multiple attribute decision making with intuitionistic fuzzy preference information [J]. System Engineering Theory and Practice, 2007, 11(11): 62−71.
[12] 徐泽水, 陈剑. 一种基于区间直觉判断矩阵的群决策方法[J]. 系统工程理论与实践, 2007, 27(4): 126−133.
XU Zeshui, CHEN Jian. An approach to group decision making based on interval-valued intuitionistic judgment matrices[J]. System Engineering Theory and Practice, 2007, 27(4): 126−133.
[13] 徐泽水. AHP中两类标度法的关系研究[J]. 系统工程理论与实践, 1999, 19(7): 97−101.
XU Zeshui. Research on the relationship between the two kinds of scaling method in AHP[J]. System Engineering Theory and Practice, 1999, 19(7): 97−101.
[14] XIA Meimei, XU Zeshui, LIAO H C. Preference relations based on intuitionistic multiplicative information[J]. IEEE Transactions on Fuzzy Systems, 2013, 21(1): 113−133.
[15] XIA Meimei. Point operators for intuitionistic multiplicative information[J]. Journal of Intelligent & Fuzzy Systems, 2015, 28(2): 615−620.
[16] YU Dejian, FANG Lincong. Intuitionistic multiplicative aggregation operators with their application in group decision making[J]. Journal of Intelligent & Fuzzy Systems, 2014, 27(1): 131−142.
[17] ZHANG Zhiming. Approaches to group decision making based on interval-valued intuitionistic multiplicative preference relations[J]. Neural Computing & Applications, 2016, 10(2): 1−41.
[18] HE Yingdong, CHEN Huayou, ZHOU Ligang, et al. Intuitionistic fuzzy geometric interaction averaging operators and their application to multi-criteria decision making[J]. Information Sciences, 2014, 259(3): 142−159.
[19] Garg H. Generalized intuitionistic fuzzy multiplicative interactive geometric operators and their application to multiple criteria decision making[J]. International Journal of Machine Learning & Cybernetics, 2016, 7(6): 1−18.
[20] 邓纯净, 谢正亮. 基于层次分析法的高速铁路车站选址评价[J]. 交通科技与经济, 2010, 12(5): 53−55.
DENG Chunjing, XIE Zhengliang. High-speed railroad station selected location appraisal based on analytic hierarchy process[J]. Technology & Economy in Areas of Communications, 2010, 12(5): 53−55.
Evaluation method for the location selection ofhigh-speed railway station based on preference information
WANG Rui1, LI Yanlai1, 2,ZHU Jianghong1
(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031, China; 2. National United Engineering Laboratory of Integrated and Intelligent Transportation, Southwest Jiaotong University, Chengdu 610031, China)
In order to research the multi-attribute decision making problem of the evaluation method for the location selection of high-speed railway station, the evaluation index system was constructed from 5 aspects of economic factors, network factors, functional factors, coordination factors and environmental factors. With respect to problem of incomplete evaluation information and inaccurate information aggregation process in the existing research, an evaluation method of the location selection of high-speed railway station based on intuitionistic multiplicative preference information was proposed. The intuitionistic multiplicative numbers were utilized to evaluate the preference information of different plans, and the intuitionistic multiplicative interaction weighted average (IMIWA) operator and the generalized intuitionistic multiplicative interaction weighted average (GIMIWA) operator were put forward combined with the operational laws of intuitionistic multiplicative numbers under the cross influence of the membership and non-membership degree of preference information. Finally, the GIMIWA operator was utilized to fuse the preference information of the high-speed railway station locationselection plans to determine the final ranking. An example was provided to illustrate the validity and rationality of the proposed method.
high-speed railway station; evaluation of location selection; intuitionistic multiplicative preference information; generalized intuitionistic multiplicative interactive weighted averaging (GIMIWA) operator
U291.61
A
1672 − 7029(2018)01 − 0008 − 09
2016−12−09
国家自然科学基金资助项目(71371156)
李延来(1971−),男,河北昌黎人,教授,从事运输系统优化理论与方法和产品规划等研究;E−mail:yanlaili@home.sujtu.edu.cn
