节日营销阵发效应下电商退换货服务定价与订货策略研究
2018-01-31,,2,
, ,2,
(1.中山大学 管理学院,广东 广州 510275; 2.仲恺农业工程学院 计算科学学院,广东 广州 510225; 3.美国德克萨斯州立大学 工业工程系,美国 圣马科斯 TX78666)
1 引言
近年来,电商通过不断创造节日刺激需求,如京东通过“618”、聚美优品通过“520”等节日吸引了全民参与狂欢。在这些节日营销期间,在线顾客需求量短时间较节前激增,2016年“双11”全天天猫的总销售额达到1770.4亿元。但销售量大幅度增加也带来节后退货量的大幅度增加。节日营销市场需求与退货的这种集中性、突发性、反常性和规模性等新特点,使得节日营销期间市场需求与退货呈现明显的阵发效应。姚灿中[1]也论证了节假日期间的大规模物流基地产品出入库间隔分布具有阵发特征。为应对这种阵发效应,电商主要通过两条渠道减少库存成本:一方面,加强对市场需求预测,但由于节日营销市场需求的不确定性,导致预测与实际交易差距较大,不得不多准备一些存货应对市场需求和退换货需求。另一方面电商通过增加在线咨询等服务降低退货率。电商的高退货率主要是因顾客在购买前不能看到、触摸、试用商品,信息不对称导致。为此,一些电商通过提供细心周到的在线咨询服务、加强产品广告宣传和购物指导,解决买卖信息不对称问题,减少顾客退换货的发生。电商提供上述服务要增加企业服务投入成本(即服务价格)。基于成本控制,电商不可能无限增加咨询费用等服务成本(价格),需要研究在综合考虑订货策略的情况下如何制订最优服务价格,从而实现收益最大化。
一些学者研究了最优定价及订、退货策略问题。部分研究将销售价格作为决策变量,假设市场需求是确定的,建立报童模型来研究库存问题[2,3]。Petruzzi和Dada[4]在市场需求随机的情况下,假设市场需求分别是销售价格的线性和非线性函数,即在加法和乘法两种需求模式下完善了报童模型的理论框架。Chen和Bell[5]将退货引入到模型中,讨论了市场需求是加法模式时企业定价以及订货策略问题。张霖霖和姚忠[6]讨论了市场需求是乘法模式时电商接受顾客退货时的定价策略和订货策略。Hall等[7]研究了零售商的动态定价与订货。Chen和Bell[8]则研究了不同退货政策对企业定价及订货决策的影响。Shulman等[9]研究了两个竞争零售商的定价和订货问题,认为需通过控制退货率来提高收益。Anderson等[10]研究了女装的在线销售,分析显示销量与顾客退货有很强的正相关性。姚泽有[11]在考虑销售努力水平和退货价格的情况下,研究了最优定价决策问题。以上研究没有考虑到节日营销阵发效应带来市场需求不确定这一情况;也没有针对电商通过增加在线咨询等服务减少退换发生率,将商品销售价格和退换货服务价格同时作为决策变量考虑定价订货策略因素。新的情况需要把退换货服务价格(成本)与订货策略统筹考虑,本文对基于报童理论的市场需求确定性收益模型进行进一步优化,为电商科学制订退换货价格与订货策略提供有效指引。
针对节日营销阵发效应,本文对基于报童理论的电商收益最大化模型进行两个方面的优化:第一,结合节日营销期间需求激增新特点,将市场需求拓展至不确定性。第二,将电商增加在线咨询服务等退换货服务价格(成本)等因素引入电商收益最大化模型,将商品销售价格和退换货服务价格(成本)同时作为决策变量,对模型进行了新改进。希望为电商企业把握增加咨询费用等服务成本(价格)和订货策略之间的最优平衡提供指导。
2 问题描述与模型构建
电商要实现节日营销收益最大化,既与市场需求密切相关,同时也与退换货服务定价、订货策略紧密相连。此外,退换货服务定价与订货策略间相互关联也共同对收益最大化产生影响。为简化研究,在电子商务交易过程中,本文考虑一个单级供应链,即由电商和顾客两个成员所组成的供应链。即某电商只销售一种商品,以价格p将商品出售给顾客,在一定日期范围内接受无理由退货,并全款退货。
2.1 拓展需求函数
借鉴以往模型,引入市场需求不确定性和电商增加在线咨询等退换货服务价格因素,将需求函数修改为
D(p,r)=f(p)·ζ+g(r)
其中p为商品销售价格,r为单位商品退换货服务价格,ζ为市场需求不确定部分的随机变量,定义区间为[A,B](A>0),并假设其均值为μ,密度函数为l(·),分布函数为L(·)。
考虑如下假设:

根据以上描述,本文假设需求函数如下
D(p,r)= (a-bp)·ζ+α+βr
(1)
其中a>0,α>0,b>1,a和α为市场基本需求量,b为商品的价格弹性指数,b越大,需求对价格改变的敏感度越高。本文考虑价格弹性的商品,因此,假设b>1。β为市场需求对退换货政策的灵敏系数,β>0表示市场需求随着r的增大而增大,即当服务价格越高,服务投入越多,退换货政策比较宽松,对市场需求的刺激也比较大。
2.2 退货函数
以往研究表明顾客退货与销量有很强的正相关性,并且顾客退货与退货价格有关。考虑到宽松的退换货政策会使退货更加容易成功,因此,本文假设退货量与退换货服务价格有关,并与对市场需求的影响敏感程度相同,即
R(r)=k0+βr
(2)
其中k0为市场基本退货量,β为退换货政策对退货量的敏感程度,即假设退换货政策对于退货量的影响与对市场需求的影响程度是一样的。
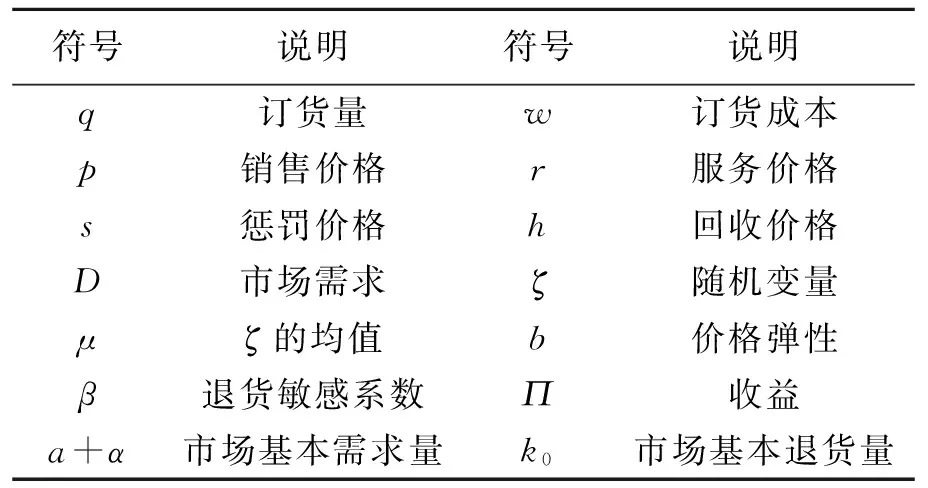
表1 变量符号及其说明
3 构建节日营销阵发效应下电商收益最大化模型
不失一般性,为简化研究先建立市场需求确定条件下电商收益最大化模型,即假设需求函数为D(p,r)=f(p)+g(r)。在此基础上,将市场需求拓展为不确定性,构建节日营销阵发效应下市场需求不确定情况下电商收益最大化模型。
3.1 需求确定条件下收益最大化模型
3.1.1 收益函数
在市场需求确定的情况下,即假设D(p,r)=a-bp+α+βr。若电商的初期订货量为q(此时q=D(p,r)),订货单位成本为w,零售商在退货服务方面的投入单价为r,用П来表示收益,则电商的最大收益函数如下
maxП =(p-w)·D-r·R
(3)
3.1.2 模型分析
定理1当β<4b时,最优整合销售价格和退换货服务价格是存在的。
证明收益函数(3)式的海塞矩阵的顺序主子式H1=-2b<0,H2=β(4b-β)>0。所以,收益函数的海塞矩阵负定,最大值存在。证毕。
定理2最优的销售价格和最优的退换货服务价格唯一确定。
证明令收益函数(3)式两边分别对p和r求偏导,令偏导数等于零并联合以上两式,化简得
(4)

根据定理2中最优销售价格和最优退换货服务价格的表达式,不难得到以下性质。

性质1说明,当β<4b时,最优订货量q*是关于退货敏感系数β的增函数,退货敏感系数越高的商品,对市场需求和退货量刺激越大,越要提高订货量。

以上分析表明,当电商加大退换货服务投入,制定宽松的退换货政策,会引起销售量和退货量的增大,但最优收益不变。因此,究竟是需要提高总体销售量还是降低退货量,将取决于电商销售产品的价格弹性。

性质2说明最优销售价格和退换货服务价格都是商品弹性b的减函数,商品的价格弹性指数越高,电商的最优定价越低,相应的退换货服务价格也越低。对于价格弹性高的商品,电商可以考虑薄利多销政策,但需要提高退货门槛,以降低退换货投入成本(价格)。
商品价格弹性b对订货量的影响与商品退货敏感性有关,当退货敏感系数比较小(β小于2)时,订货量随着商品价格弹性的增大而减少,当退货敏感系数比较大(β大于2)时,订货量随着商品价格弹性的增大而增大。这也说明,退货敏感系数比较小时,服务投入对于退货量和市场需求的影响比较小,此时,弹性越大的商品所需订货量越低。退货敏感系数比较大时,服务投入对于退货量和市场需求的影响比较大,此时,弹性越大的商品所需订货量越大。即商品的价格弹性指数越大,电商的订货量就越大,这无疑增加了电商的库存成本,并不利于收益的提高。

3.2 建立阵发效应下市场需求不确定收益模型
在节日营销下,市场需求呈现阵发效应并难以预测,需要将上述市场需求确定性条件下收益模型拓展至不确定性,研究建立市场需求不确定下收益模型。
3.2.1 收益函数
在市场需求不确定的情况下,假设电商的初期订货量为q,订货单位成本为w,零售商在退换货服务方面的投入单价为r,若期末过剩,则以单价h退回到上级供应商,若缺货则以单价s来进行惩罚,假设h (5) 3.2.2 模型分析 (6) 令(6)式等于0,当ζ≤z时,可得D1。即当需求D在区间[0,D1]时,模型收益为负;当需求D在区间[D1,q]时,模型收益为正。当ζ>z时,可得D2。即当需求D在区间[q,D2]时,模型收益为正;当需求D在区间[D2,+∞]时,模型收益为负。 用E(Π)来表示期望收益,表达式为 (7) (2)通过培养探索创新精神,使学生与时俱进。随着信息化时代的到来,我们只有不断培养学生自主探究学习的能力,才能使学生具备处理并使用信息资源的能力。所以,体育教师应当为学生们营造一个轻松愉悦、自由民主的学习氛围,使学生们在这片学习的海洋中充分展现自我,努力培养他们探索和创新的精神,使其能够找到适合自身学习的方法,这对于在求学路上的每一位学生来说都是至关重要的。 E(Π)=(p-w)(a-bp)μ-(a-bp)(w-h)Λ(z)+ (p-w)(α+βr) (8) 从而(8)式对于z的一阶和二阶偏导数为 (9) (h-r-s)(k0+βr)l(z) (10) (11) 存在唯一的最优解z*(p,r)。因而,对于最优化问题(11)式,可以采用两阶段法求解,先求得z*(p,r),再将z*(p,r)带入E(П*),求解最优的p和r。 令(9)式=0,得到(a-bp)[h-w+(p+s-h)·(1-L(z)]+s(k0+βr)+(h-r-s)(k0+βr)·L(z)=0,即 (12) 给定z,(11)式关于p,r的一阶导数为 b(s-w)Θ(z*)-(a-2bp)Θ(z*)+(α+βr) (13) (14) (11)式关于p,r的二阶导数为 (15) 定理3对于给定的z,当4b[μ-Θ(z*)]L(z*)>β时,电商收益期望在点(p*,r*)的海塞矩阵是负定的,从而,存在满足一阶条件(13)和(14)式的最优销售价格和退换货服务价格使得收益期望达到最大。 证明由于其海塞矩阵为 所以要使海塞矩阵为负定,需要验证两个条件:(1)H1<0;(2)H2>0。 =[-2bμ+2bΘ(z*)]·[-2βL(z*)]-β2 =[4b(μ-Θ(z*))L(z*)-β]β>0 因此,电商收益期望在点(p*,r*)的海塞矩阵是负定的,从而,存在最优销售价格和退换货服务价格使得收益期望达到最大。 推论1在需求随机环境下,当β<2b时,销售价格和退货投入价格都大于确定性环境下的相应价格。 证明令(13)式=0,(14)式=0,得到最优销售价格和最优服务价格表达式 此时,若将3.1节确定性问题得到的最优解记为 令J=2(a+bw)μL(z*)+2b(w-h)Λ(z*)L(z*)+ 2b(s-w)Θ(z*)L(z*)-2aΘ(z*)L(z*)+2αL(z*) K=-k0L(z*)+βhL(z*)+sβ[1-L(z*)]-wβ M=2bw+2a+2α,N=-βw-k0 由于市场需求随机性情况下对于参数敏感性的分析解析式比较复杂,因此,本文将在第4部分给出数值实验,试图通过数值分析得到一些新的启示。 表2 外生的市场参数 实验结果表明其它条件不变时,退货服务的敏感系数越高,电商最优销售定价越高,最优订货量也越高,退换货服务价格也越高。数值试验显示的这一结果与 3.1节中性质1的证明基本吻合。实验结果所显示的最优收益与销售价格和退换货服务价格的变化情况表明,销售价格与退换货服务价格存在着最优配置,并不是在退换货服务方面的投入越高越好,只有销售价格与服务投入达到均衡,电商企业的收益才能得到提高。因此,相对宽松的退换货政策对电商发展或许更具战略意义。 研究取得了如下成果:第一,建立了节日营销需求阵发效应下的电商收益最大化模型。针对目前电子商务节日营销中日益严重的退货现象,假设市场需求同时与商品销售价格和退换货服务价格密切相关,并且退货量是退换货服务价格的增函数,基于报童模型理论建立了市场需求阵发效应下电商收益最大化模型。第二,给出了模型解的相关表达式。在市场需求确定的情况下发现最优退换货服务价格不能超过最优售价的一半,并研究了退货敏感系数和商品价格弹性对最优销售定价、退换货服务定价、订货量和收益的影响;在市场需求随机的情况下证明了最优价格的唯一存在性并给出了解析表达式,证明了在β<2b的条件下,市场需求不确定性情况下的最优价格大于确定性情况下的最优价格,并对参数敏感性进行了数值试验。第三,研究了销售价格、退换货服务价格、订货量与退货敏感系数之间的最优平衡关系。结果表明,最优销售价格是退货敏感系数的增函数,退换货服务价格和订货量都与退货敏感系数正相关。另外,电商为了应付市场需求随机性会提高销售价格和加大退换货服务投入。 研究可为电商开展节日营销制定服务价格和订货策略最优平衡,进而制订科学退换货政策实现收益最大化提供指引。第一,电商可依据模型制定节日营销最优销售价格、退换货服务价格和订货量,掌握增加在线咨询等服务成本与订货策略之间实现最优平衡方法,避免过多服务投入给企业带来的成本压力。第二,指导电商节日营销制定符合企业实际的退货政策。建议电商企业对于弹性较低的商品制定较为宽松的退货政策,加大退换货服务投入并对于弹性相对较高的商品制定相对较高的退货门槛来获得高收益。为此,电商需要根据价格弹性和退货敏感情况,及时调整最优策略以期获得高收益。第三,指导电商节日营销制定差异化的服务以有效降低退换货率。比较有效的方法是通过高品质个性化的服务控制顾客退货率。主要方式有:提高物流服务水平,减少由于物流管理问题而导致的顾客退货;提高宣传咨询服务水平,减少因商品信息与实物不对称而导致的顾客退货;对于昂贵且高弹性商品如化妆品及奢侈品等提高退货门槛或者退货麻烦度,防止个别顾客的恶意退货;提高产品质量和品牌影响力,培养忠实顾客,稳定市场,从源头上减少退货事件的发生等,从而提高电商的收益。 由于数据的限制,为简化研究,对退换货服务价格对市场需求的影响与退货量相同的假设存在过于理性化的问题,制约了模型运用的范围。研究今后可从以下几个方面做进一步的探讨:(1)考虑同一商品同时在售时,多个电商博弈的退货定价决策问题。(2)市场需求、退货量是销售价格和退换货服务价格的一般函数时,电商的退换货定价决策问题。对这些问题的深入研究有助于电商节日营销阵发时优化退换货管理,使退换货物流研究更加贴近现实。 [1] 姚灿中.物流系统出库行为动力学的统计特征分析[J].复杂系统与复杂性科学,2014,11(4):80- 86. [2] Whitin T. Inventory control and price theory[J]. Management Science, 1955, 2(1): 61- 68. [3] Vlachos D, Dekker R. Return handling options and order quantities for single period products[J]. European Journal of Operational Research, 2003, 151(1): 38-52. [4] Petruzzi N C, Dada M. Pricing and the newsvendor problem: a review with extensions[J]. Operations Research, 1999, 47(2): 183-194. [5] Chen J, Bell P C. The impact of customer returns on pricing and order decision[J]. European Journal of Operational Research, 2009, 195(1): 280-295. [6] 张霖霖,姚忠.考虑顾客退货时在线企业的定价与订货策略[J].管理科学学报,2013,16(6):10-21. [7] Hall J M, Kopalle P K, Krishna A. Retailer dynamic pricing and ordering decisions: category management versus brand-by-brand approaches[J]. Journal of Retailing, 2010, 86(2): 172-183. [8] Chen J, Bell P C. Implementing market segmentation using full-refund and no-refund customer returns policies in a dual-channel supply chain structure[J]. International Journal of Production Economics, 2011, 136(1): 56- 66. [9] Shulman J, Coughlan A T, Savaskan R C. Managing consumer returns in a competitive environment[J]. Management Science, 2011, 57(2): 347-362. [10] Anderson E, Hansen K, Simister D, et al.. How are demand and returns related?Theory and empirical evidence[R].Working Paper, Kellogg School of Management, Northwestern University, February, 2006. [11] 姚泽有.考虑努力及退货价格因素的易逝品供应链退货政策模型[J].预测,2010,29(6):48-56.

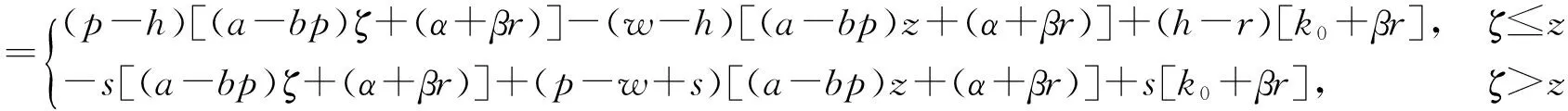















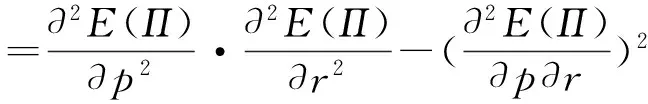




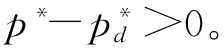
4 数值实验


5 结论与讨论
5.1 研究成果
5.2 管理学启示
5.3 研究局限与展望
