基于心音周期性的自动分段研究

2018-01-29许莉莉郭学谦

中国医疗设备 2018年1期

许莉莉，郭学谦

首都医科大学生物医学工程学院，临床生物力学应用基础研究北京市重点实验室，北京 100069

引言

有研究表明，某些心血管疾病在心电图表现出异常之前，就出现心脏杂音和心音变异。杂音的出现和心音变异包含着丰富的病理信息[1]。因此，心音信号可作为临床辅助评估心脏功能状态的基本参数。人体心音信号是心动周期中，心脏瓣膜的开关、肌腱和肌肉的舒张、血流的冲击以及血管壁的振动而产生的一种复合音，一个心动周期中包括4个心音，通常称为S1（第一心音）、S2、S3和S4，多数情况下只能听见S1和S2[2]。

心音信号分析处理的首要任务就是提取独立的心动周期。现有的心音分段方法有两类，一类是以心电图作为参考进行分段，这类方法效果较好，但对硬件要求高，具有很大的局限性[3]；另一类方法以心音包络为基础进行分段，目前大多报道采用的都是此类方法[4-6]。这类方法多采用HHT变换或者小波变换提取心音样本的能量信息，导致包络不平滑或者分段模糊。事实上，心音的分段无论采取什么样的方法也脱离不了心音信号本身的周期性[7]。心音是非平稳的类周期信号，即使出现杂音或者发生异常，一般也体现出明显的周期性，2例异常的心音和一例正常心音，见图1。本文正是基于心音信号的周期性自动提取心动周期。

1 算法介绍

1.1 形态滤波提取心音包络

数学形态学在二维图像处理中应用非常广泛，它包括4种基本运算：膨胀、腐蚀、开运算和闭运算，是利用一个结构元素去探测图像，去量度和提取图像中的对应形状以达到对图像分析和识别的目。正因为数学形态学是分析图形几何形状和结构的数学方法，近年来它也被用于提取一维信号的包络[8-11]。

图1 心音信号

将数学形态学推广到一维信号处理，其基本的膨胀、腐蚀、开运算和闭运算定义如下[11]：设F，S分别为一维信号和一维结构元素，其长度分别为N和M，一般N＞M，则F被S膨胀为：

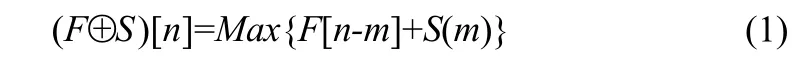
其中n=M,…, N; m=0,…M-1。具体的运算过程为：平移结构元素至n点处，将结构元素与信号序列对应数据点相加，取相加结果的最大值。由上述运算可知，一维信号前端的M个数据点未进行膨胀。

F被S腐蚀：

式中n=0,…,N-M; m=0,…M-1。具体的运算过程为：平移结构元素至n点处，信号序列与结构元素对应数据点相减，取相减结果的最小值。由上述运算可知，一维信号末端的M个数据点未进行腐蚀运算。

开运算是指对一维信号先腐蚀再膨胀，闭运算则是指对信号先膨胀再腐蚀。

本文所用心音样本长度均为5 s，一个心动周期的平均时间约为0.8 s，一个5 s的心音样本应该包含6个左右心动周期。考虑到心动过缓导致的心音变异等，本文对一个样本提取4个心动周期的信息。将原始心音信号基线置零，再将信号按基线取绝对值，最后将整段信号按强度归一化处理，即“全波整流”。为了减少每次处理的数据量，将信号下采样至1102.5 Hz。预处理后的心音信号，采用闭运算提取其包络。闭运算先采用结构元素膨胀，填充信号内相邻峰值间的细小沟壑；再采用结构元素腐蚀，平滑峰值间的细小突出。经过预处理与闭运算后，获得一维心音信号的包络，见图2。

1.2 相关计算提取峰位

信号处理中，相关函数的应用广泛，包括信号中隐含周期性的检测、噪声中信号的提取等[12-13]。其定义如下：

图2 一维心音信号包络

相关计算进一步平滑了心音信号包络上的毛刺、沟壑。经过形态学闭运算提取的心音包络仍然带有毛刺，并不适合做进一步的周期提取。为了突出信号的周期性，用于自动分段，本文采用一种自适应的相关计算，突出其峰值位置。即提取每个心音信号各自的主峰片段与整个包络做相关运算，则整个信号中与主峰形状相似的峰位将被突出。以图2a为例，图中主峰为持续时间较长的方形峰，提取该方形峰与图2a整段包络做相关计算后，方形峰起始位置成为相关系数极值位置，见图3。

图3 提取主峰片段进行相关运算结果

1.3 基于周期性的自动分段

心音自动分段是基于心音信号的周期性。一般来说，每个心动周期中，峰值的间期相对稳定而各不相同。在图2中标记出相关计算后的局部极值，按顺序标记为P1，P2，…。首先将P1看作第1个心动周期的第一个峰值，将P2看作第2个心动周期的第一个峰值，两者之间的时间为一个心动周期T1；将P3看作第3个心动周期的第一峰，P2和P3之间的时间间隔，为第二个心动周期T2，T2应与T1大致相等，若两者大致相同，则相应的P4与P3，P5与P4之间的时间间隔大致相同，若T2应与T1明显不同，说明P2可能是第1个心动周期的第二个峰，此时，将T1改为T11，T2改为T12；将P3标记为第2个心动周期的第一个峰，P4标记为第2个心动周期的第二个峰，P5标记为第3个心动周期的第一个峰，分别记录P3P4间隔为T21、P4P5间隔为T22，若T21与T11，T22与T12大致相同，则相应的P5P6、P7P8之间的间隔大致相同，P6P7、P8P9之间的间隔大致相同；若T21与T11、T22与T12明显不同，说明P3是第1个心动周期的第三个峰，则P4、P5、P6分别看作第2个心动周期的第一、二、三峰；将P3P4之间的间隔改为T13，将P4P5、P5P6、P6P7之间的间隔分别标记为T21、T22、T23，比较T21与T11、T22与T12、T23与T13是否大致相同，依次类推。确定出每个心动周期的长度，从而自动标记出每个心动周期的起始位置，见图4。如图4a所示，图中菱形标记为前5个心动周期的起点。

图4 峰位的后处理结果

1.4 峰位的后处理

每一个心动周期被标记出来以后，在周期内根据心音的生理学特征调整S1和S2的位置。根据心电图资料：心脏收缩期的持续时间即S1结束到S2开始，小于舒张期的持续时间即S2结束到S1开始；心脏收缩期的时间基本稳定，当心动过速时，舒张期缩短，以致收缩期和舒张期的时间几乎相等，此时S1增强，S2减弱[11,14-15]。

当一个心动周期中，有两个以上的峰值，则根据4个周期内相应峰位的平均幅值，留取最强的两个峰位，利用S1S2间距小于S2S1间距来判断，两者间距相差0.1 s以上，间距小的是S1S2；两者间距相差0.06 s以下，取周期内幅值强的为S1。处理后，每个心动周期内的心音标记如图4b所示，三角形标记为每个心动周期的的S1，方形标记为S2。

2 结果和讨论

本研究采用的心音有两部份来源，共48例，其中10例异常心音从互联网下载，其采样频率为22050 Hz[16]；另外38例采自由北京市宣武医院体检显示无心血管疾病的健康人群。心音信号采集时将HKY-60C 型心音传感器（合肥华科电子技术研究所研制）放在心尖区，在家用电脑上通过Cool Edit Pro2.0软件直接录制，采样频率为11025 Hz。实验中对上述每例心音提取两个时长5 s的样本，共96个样本进行了自动分段和S1、S2的识别，其结果由北京友谊医院的专家进行鉴定。实验结果表明该算法对于正常心音的分段以及S1、S2的识别正确率达到100%。对于异常心音，如图1a所示，经相关计算后周期内只有一个极大值，未计入正确率计算外，还有一例收缩中期出现的喀啦音因幅值较高，未被正确识别外，其他异常心音均能正确分段且识别出S1、S2，算法对异常心音的正确率为89%。

该算法将数学形态学和主峰片段相关计算相结合自动提取心音信号的包络，标记出心动周期的起点，回避了其他算法中由于包络不平滑，毛刺等对后期处理的问题[17]，能够快速便捷的对心音信号进行分段和识别，为后期提取心音信号的各类特征进行心音正常和异常识别提供了基础。

3 结论

本文基于人体心音信号的周期性，提出了数学形态学运算提取心音包络，并提取包络各自的主峰片段与信号进行相关计算以突出心音周期性的方法，对心音信号进行了基于周期性的自动分段。经过48例心音共96个样本的检验，该算法能有效地进行心音分段，并正确识别出每个心动周期中的S1和S2峰，可用于心音正常和异常识别的前期特征提取。

[1] Solomon LW.Yale university school of medicine heart book[J].Yale J Biol Med,1992,65(5):537.

[2] 罗建仲,罗琳.心脏听诊[M].北京:人民卫生出版社,2000.

[3] Lehner RJ,Rangayyan RM.A three-channel microcomputer system for segmentation and characterization of the phonocardiogram[J].IEEE Trans Biomed Eng,1987,34(6):485-489.

[4] 陈洁,侯海良,罗良才,等.一种新的HHT在心音包络提取中的应用[J].中国医学物理学杂志,2012,29(2):3272-3275.

[5] 李江,李晓玉.基于HHT的心音分段和医学指标提取[J].控制工程,2015,22(1):164-169.

[6] 胡晓,王威廉.基于小波变换心音定位[J].生物医学工程与临床,2002,6(4):181-184.

[7] 武伟宁,陈若珠.基于周期提取的心音分段方法[J].北京生物医学工程, 2015,34(1):59-63.

[8] 张笑东,蒲宝明,霍红,等.均值滤波和形态学在振荡脉搏波提取中的应用[J].计算机系统应用,2016,25(2):157-161.

[9] 张柯欣,王雪峰,魏巍,等.基于数学形态学的病理性附加肺音时频谱图分析[J].中华中医药学刊,2016,34(7):1550-1552.

[10] 高艳,胡阳.基于数学形态学方法的心电图波形分离技术[J].生物医学工程杂志,2001,18(1):55-59.

[11] 郭兴明,陈剑,肖守中.基于数学形态学的心音信号识别方法[J].生物医学工程学杂志,2004,1221(5):832-835.

[12] 徐维超.相关系数研究综述[J].广东工业大学学报,2012,29(3):12-17.

[13] 葛新成,罗大成,曹勇.相关函数在数字信号处理中的应用[J].电光与控制,2006,13(6):78-80.

[14] 吴玉春,杨亚萍,邓北川.心音信号分段规则的探讨[J].北京生物医学工程,2014,33(5):524-526.

[15] 高攀.基于心音的病理特征研究[D].秦皇岛:燕山大学,2012.