梯度匀场参数优化及其在非人灵长类动物磁共振成像中的应用

俞文文，王征，聂生东

1.上海理工大学 医疗器械与食品学院，上海 200093；2.中国科学院上海生命科学研究院 神经科学研究所，上海 200031

引言

近年来，磁共振成像（Magnetic Resonance Imaging，MRI）技术得到飞速发展，已成为开展脑科学研究最为重要的影像方法之一。其中，基于血氧水平依赖的功能磁共振成像（Blood Oxygen-Level Dependent Functional Magnetic Resonance Imaging，BOLD fMRI）、扩散张量成像（Diffusion Tensor Imaging，DTI）以及磁共振波谱（Magnetic Resonance Spectroscopy，MRS）技术的发展，使MRI从简单的解剖结构显示延伸到了基于脑功能的皮层定位、基于水分子扩散模型的脑白质纤维追踪以及基于化学伪影的神经递质定量检测等范畴，成为了当今研究神经系统和脑功能的多面手。

由于进化上相近，非人灵长类的脑结构、功能活动等多方面与人类非常相似，通过使用猕猴等非人灵长类动物开展MRI研究脑功能网络及其高级认知功能是未来神经科学发展的重要方向[1-2]。但与人类的大脑相比，猕猴的脑体积小（几乎是人脑体积的二十分之一），且颅骨几何形状不规则，尤其是眶额、颞叶附近空腔较大。除此之外，猕猴额叶区域的非均质结构包括额叶静脉窦、骨头、皮下脂肪以及骨髓等，大面积覆盖着额部，从而导致磁共振图像中该区域的磁敏感效应远逊于人脑。在以往使用3.0 T MRI设备开展的猕猴实验中，所采集的BOLD fMRI和DTI图像中明显观察到了眶额区域的几何畸变、信号损失、“模糊伪影”，这些都是由于局部磁场不均匀性引起的，而正是因为猕猴额部头骨的大面积不规则几何结构以及解剖结构导致了局部磁场均匀性差。

由于没有专门针对非人灵长类动物的MRI设备，目前大多此类实验都是直接使用临床MRI设备完成的。以西门子临床用机器为例，其自带的三维匀场方法是为人体成像设计的，单个体素分辨率为7.8 mm×7.8 mm×7.8 mm。对于非人灵长类动物的脑体积而言，这一设置过于粗糙，不能够准确地计算补偿。为在此基础上进一步优化匀场效果，在以往开展的动物扫描实验中，通常进一步通过人工交互式实时匀场方式，仔细调整各阶匀场电流大小，并通过氢质子共振峰半高宽来判断匀场效果。常规方式往往非常耗时，无形中增加了麻醉动物的实验时间，从而增加实验风险；另外一方面，匀场质量高度依赖于操作者的经验以及样品的性质。

基于以上原因，本文尝试在3.0 T MRI设备上优化匀场序列参数，借助体模验证匀场效果，并进一步将优化参数方案应用于猕猴的活体实验中，在改善匀场效率的同时，提高脑功能研究中常用的BOLD fMRI、DTI扫描的图像信噪比，减小由于磁场不均匀性导致的图像伪影。

1 匀场简介

主磁场的均匀性是MRI磁体的一个重要技术指标。在MRI设备中，磁场均匀性直接影响MRI图像的信噪比、几何畸变以及核磁共振谱线宽度和谱线分辨能力。尽管在理论设计时可以做到完美均匀，但在实际加工制造磁体时，工艺误差是不可避免的。目前，工程上进行补救的方法是匀场（包括被动匀场、超导匀场），即通过补偿校正把产生的偏差补偿到接近为零，以使其尽可能恢复到设计值。

除了主磁场本身的均匀性外，即使磁体腔内被理想地看作一个均匀磁场空间，当被测物（人或动物）进入磁场后，由于生物体内存在着各种在磁场中表现为顺磁性和抗磁性的组织，在它们的界面上磁化率突变也会引起局部磁场的不均匀性，产生磁化率效应，从而引起信号损失和图像几何畸变伪影。针对这种情况，应进一步使用室温匀场[3]，即通过给匀场线圈施加适当的电流，利用线圈周围产生的微小磁场，对主磁场进行修正从而调整磁场均匀性，这种方式又称为电阻匀场。室温匀场一般用于动态的精细匀场，即在扫描时对被测对象磁化率梯度引起的不均匀性进行匀场，优点是用户可自行调整匀场电流，更灵活地校正由于被测试样品引入的局部磁场不均匀。

MRI发展到今天，在众多科研工作者的共同努力下，陆续设计出各式各样的室温匀场方法，如搜索匀场[4-5]、基于场图的匀场[6-11]、动态匀场[12-14]、z-匀场[15-18]等。本文中所使用的三维梯度匀场法属于基于场图的匀场技术，具体是通过成像脉冲序列，获得被测物在空间各点上的磁场不均匀项分布（即相位差成像[19]），再根据x、y、z匀场线圈产生的特定磁场大小及空间分布，计算出最优化的各个匀场线圈电流组合，从而补偿样品在空间各点上存在的磁场不均匀性。基于此，通过分析B0场图的谐波成分（即ΔB0），以此计算并调整各匀场线圈中的电流，从而实现自动匀场。该方法最早由Prammer等[7]提出，后续研究者又在此基础上进行了深入改进[8,20-24]。目前许多临床磁共振成像设备都是采用这一类方法进行自动匀场。

2 材料与方法

2.1 设备与实验对象

所有磁共振实验均使用SIEMENS公司Tim Trio 3.0 T MRI系统，内置体线圈作为发射线圈，实验室自制8通道相控阵线圈作为接收线圈。

为更好的验证实验效果，本次使用美国放射学会（American College of Radiology，ACR）小体模（全塑料材质，专为尺寸较小线圈，如膝线圈、四肢线圈、乳房线圈等测试使用，外径4.5英寸，圆筒长4.5英寸，内部包含复杂几何结构以及空腔）进行测试，借助其内部的复杂集合结构、空腔，模拟活体动物头部复杂情况，验证匀场效果。

本次实验选取健康成年食蟹猴1只（性别：雄性，年龄：6.8岁，体重：5.5 kg）。食蟹猴（学名：Macaca fascicularis），也称长尾猕猴，属于灵长目猴科，猕猴属。该实验动物营养状态良好，精神状态佳，无神经系统病史。

2.2 动物实验步骤

磁共振实验前12 h禁食、水，以防止动物麻醉状态时堵塞呼吸管道。采用氯胺酮诱导麻醉，剂量10 mg/kg，肌肉注射，随后行气管插管，并将动物头部固定在实验室自制的立体定位仪上，打开磁共振兼容电热水毯维持体温，打开呼吸机及监护系统监视生命体征各项指标，同时给予异氟烷气体（浓度1%～1.5%）维持麻醉。准备结束后，将动物头部置于接收线圈内正中，送入磁体腔内，开始磁共振扫描。以上动物实验所有规程均经过中国科学院上海生命科学研究员生命科学伦理委员会批准。

2.3 匀场实现及参数设置

借助梯度回波序列快速、易操作及其对B0场偏差高度敏感等优势，常采用双回波三维梯度回波序列测量被测物感兴趣区域内的ΔB0场图，见图1。

图1 双回波三维梯度回波序列时序图

在不均匀磁场中采集到的数据将受到不均匀磁场ΔB0的相位调制，即局部磁场不均匀性将改变该区域中共振信号的相位。处理两次采集的回波得到两幅相位数据图，将两次所得到的相位图相减，即有：

经相位解卷绕后[25]，长、短两个回波各自相位成像，两幅相位图对应空间位置上的像素逐个相减，即可得到与磁场偏差成比例的ΔB0分布场图[26]，列式如下：

除了获得表征当前磁场空间分布的相位差数据，梯度匀场的实现还需要读取机器各个匀场线圈通入单位电流（1 A）对磁场影响的场图数据，以及计算能使匀场区域内磁场不均匀性最小化的匀场电流。整体的匀场计算实现流程，见图2。

图2 梯度匀场流程

本次实验中主要对比了系统自带三维匀场方法与参数优化后的高分辨率梯度回波匀场方法，主要参数设置的如下：系统自带三维匀场方法采用双回波稳态序列，视野大小500 mm×350 mm×500 mm，编码矩阵64×48×64，空间分辨率78 mm×78 mm×78 mm；参数优化匀场方法采用三维梯度双回波序列，视野大小128 mm×128 mm×128 mm，编码矩阵64×64×64，空间分辨率2 mm×2 mm×2 mm，重复时间为10 ms，回波时间分别为，TE1=2.2 ms，TE2=4.4 ms。

2.4 磁场均匀性测量

当射频脉冲结束后，氢核自旋开始自由进动和弛豫，受自旋—自旋弛豫过程影响，这时接收线圈中感应到的交变电流会慢慢衰减直至消失，此衰减的交变电流称为自由感应衰减（Free-Induction Decay，FID）信号。磁场的不均匀性会直接影响FID信号的持续时间，从而影响到FID的面积。通过对时域FID信号进行傅里叶变换，可以得到频谱图。而该频谱图的半高宽（Full Width at Half Maximum Height，FWHM）常用来作为磁场均匀性的判断标准。即磁场均匀性越好，FWHM越小。

3 结果

3.1 体模实验

通过对ACR水模先后共10次的测试，不同匀场方法测量得到的FWHM结果，见表1。水模初始进入磁场中的状态为装机调试场（出厂设置），此时测得的FWHM为（105.65±1.047）Hz，使用系统自带三维自动匀场方法（DESS序列）后测得的FWHM可以达到（30.58±0.414）Hz，使用经过参数优化后的匀场方法（mGRE序列）后测得的FWHM可以达到（19.97±0.452）Hz。

不仅在定量指标上看到变化，比较两种方法在匀场前后的场图，也能直观、形象的看到差别，见图3。图中第一列显示了磁共振信号幅值图（图3a），第二到第四列分别显示了主动匀场前（图3b）、三维自动匀场后（图3c）以及参数优化匀场后（图3d）的场图，上述3组场图均为两次TE得到的相位图接缠绕后相减计算得到的相位差值图。所有图像均在3.0 T磁共振设备上使用双回波三维梯度回波序列采集（图像分辨率2 mm×2 mm×2 mm），第一至第三行分别显示了横断位、冠状位以及矢状位层面。为便于观察，图中使用伪彩显示相位在+π～-π范围内的变化值。可以发现，在体模的液体与空气交界面附近有明显的场相位变化，随着匀场的优化，在界面处变化趋于平缓，不均匀区域明显减小。

3.2 动物实验

非人灵长类动物的头部，尤其是眼眶上缘区域明显比人类的头部覆盖更厚的肌肉，见图4。其中，图4a显示了活体动物结构像的磁共振信号幅值图，图中第二、三列分别显示了三维自动匀场后（图4b）以及参数优化匀场后（图4c）的相位差值情况。两组图均在3.0 T磁共振设备上使用gre-field-mapping序列采集（图像分辨率2 mm×2 mm×2 mm），第一至第三行分别显示了横断位从上至下的3个不同层面。当使用以平面回波为基础的序列成像时，尤其在眼眶附近图像畸变严重，常规三维匀场后，在场图上仍然这些对应的区域场仍然场均匀性较差（图4b）。使用参数优化匀场后，尤其在眶额附近区域，场的均匀性得到改善（图4c）。

表1 三维自动匀场方法和参数优化采样后匀场方法匀场效果定量比较

图3 匀场前后的ACR体模场图对比

经过有效的匀场，使用平面回波序列采集的图像畸变将得到改善，见图5。图5a显示了常规匀场后的回波平面成像（Echo-Planner Imaging，EPI），图5b显示了参数优化匀场后的EPI图像。两幅图均在3.0 T磁共振设备上使用BOLD_EPI序列采集（图像分辨率2 mm×2 mm×2 mm），第一至第三行，自左至右分别显示了横断位自上至下连续无间隔的9个不同层面。通过采集猕猴全脑的BOLD fMRI图像可以证明，匀场效果较差时，表现出全脑图像在相位编码方向的几何畸变，从眼球形状可以明显看出，图像被拉伸（图5a）；在匀场效果较好时，伪影减轻，图像几何畸变不再明显（图5b）。

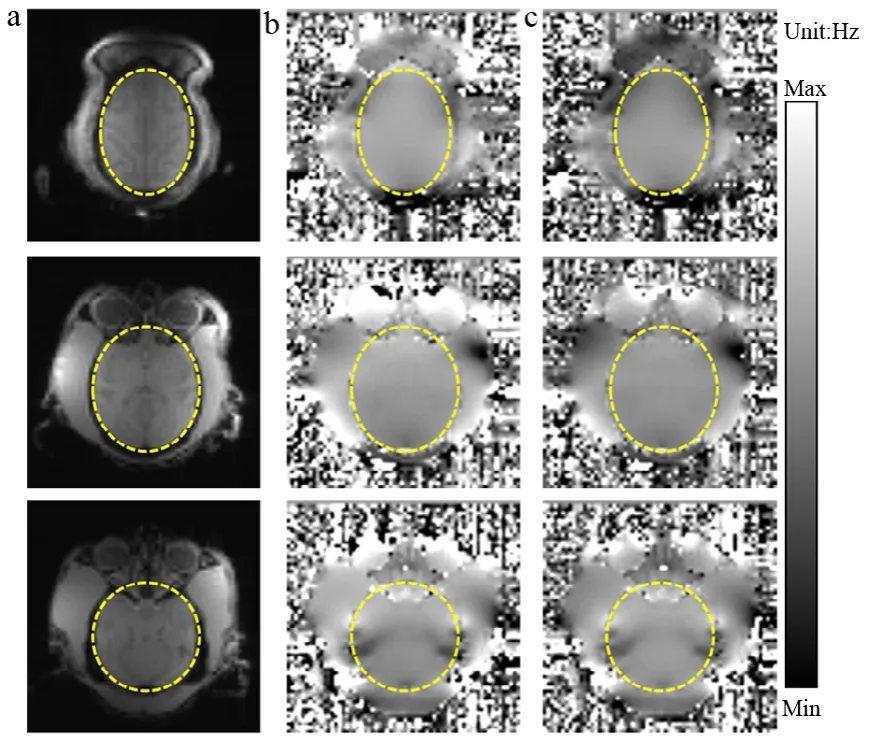
图4 成年猕猴头部场图对比

图5 匀场后的成年猕猴头部BOLD EPI图对比

4 讨论

一般情况下，高分辨率梯度匀场都能取得较好的匀场效果，但也存在不足，主要体现在以下几个方面：① 某些特殊情况下，如动物头部因外科手术引入含磁性物质（如骨钉、牙科水泥等）导致磁场均匀性严重破坏时，由于采用了梯度回波序列，因此无法获得理想的磁场分布图像；② 由于空间分辨率较高，图像信噪比往往较低，由于相位解卷绕算法是一种非线性算法，其误差具有传递性，当相位数据信噪比较差时，其解卷绕后的数据也将变得不准确，这将大大影响匀场计算的效果；③ 由于采用了XY方向的相位编码，扫描及计算所需时间较长，不适合对大尺寸样品进行匀场。针对以上问题，目前已有相关的技术解决方案：例如，在磁场非常不均匀的情况下，采用自旋回波脉冲序列替代常规的梯度回波脉冲序列；为缩短三维梯度匀场的时间，在相位编码时采用非均匀采样在K空间上加速。

当然，对于单体素MRS来说，对整个头部区域采集完整的三维B0场图是多余的，而且可能并非最优的方案。因此，Gruetter等[8-9]提出了一种快速自动匀场技术——投影映射快速自动匀场技术（Fast, Automatic Shimming Technique by Mapping Along Projections，FASTMAP）， 区别于上述需采集整幅∆B0分布图像的匀场方式，这种方法基于一种稀松，但是高效的采集方式，即只沿6个方向投影测量∆B0，这样可以在有效缩短获取静磁场信息所需时间的同时，提取必要的一阶、二阶匀场线圈最佳电流调整信息。在此基础上，后续又出现了提高效率和可靠性的投影映射快速自动匀场技术[10]和使用任意映射采集参数的鲁棒自动匀场技术。这些基于FASTMAP的优化改进方法或提升了精确性，或进一步缩短了采集时间，又或将其应用扩展至二维层面匀场[11]。

为了获得更好的非人灵长类动物匀场效果，本文也尝试了各种匀场方法的组合，并在实际操作过程中发现：①与体模相比，动物实验扫描信噪比较弱，个别情况下，单独使用高分辨率参数匀场并不能显著提高匀场效果，可以尝试结合高分辨率参数与手动交互式匀场，实验结果显示，组合使用两种方法较单独使用任一种方法，能更高效的达到预期的匀场效果；② FASTMAP适用于较小体积内的快速匀场，在相对大的测试区域内，无法达到理想的匀场效果，为了获得更好的匀场效果，可以重复3～4次，如果仍然无法满足半高宽要求，可以结合手动交互式匀场再进行细微调整。

5 结论

磁场均匀性是磁共振技术的基础，也是平面回波成像、弥散成像、波谱分析等一系列序列实现的前提条件。本研究采用梯度回波序列，通过序列参数优化，提高空间分辨率，缩小匀场范围，能够帮助优化局部匀场效果，进而减小由于磁场不均匀导致的畸变。该方法较常规三维匀场序列参数，能够在细节上更好的处理匀场电流补偿，在非人灵长类动物等头部尺寸较小、匀场要求更高的情况下，能够一定程度上提高匀场效果。本文研究结果，可为非人灵长类动物脑功能成像的优化提供参考。

[1] 胡新天,仇子龙,顾勇,等.非人灵长类模型[J].中国科学院院刊,2016,31(7):773-782.

[2] Lv Q,Yang L,Li G,et al.Large-scale persistent network reconfiguration induced by ketamine in anesthetized monkeys:relevance to mood disorders[J].Bio Psychiat,2016,79(9):765-775.

[3] Anderson WA.Electrical current shims for correcting magneticɦelds[J].RSI,1961,32(3):241-250.

[4] Nelder JA,Mead R.A simplex-method for function minimization[J].Comput J,1965,7(4):308-313.

[5] Ernst RR.Measurement and control of magnetic field homogeneity[J].RSI,1968,39(7):998-1012.

[6] Sekihara K,Matsui S,Kohno H.A New method of measuring static-ɦeld distribution using modiɦed fourier nmr imaging[J].J Phys E Sci Instrum,1985,18(3):224-227.

[7] Prammer MG,Haselgrove JC,Shinnar M,et al.A new approach to automatic shimming[J].J Magnetic Resonance,1988,77(1):40-52.

[8] Gruetter R,Boesch C.Fast,noniterative shimming of spatially localized signals-in vivo analysis of the magnetic-field along axes[J].J Magn Reson,1992,96(2):323-334.

[9] Gruetter R.Automatic localized in vivo adjustment of all 1st-order and 2nd-order shim coils[J].Magn Reson Med,1993,29(6):804-811.

[10] Shen J,Rycyna RE,Rothman DL.Improvements on an in vivo automatic shimming method (FASTERMAP)[J].Magn Reson Med,1997,38(5):834-839.

[11] Klassen LM,Menon RS.Robust automated shimming technique using arbitrary mapping acquisition parameters (RASTAMAP)[J].Magnet Resonan Med,2004,51(5):881-887.

[12] Blamire AM,Rothman DL,Nixon T.Dynamic shim updating:a new approach towards optimized whole brain shimming[J].Magn Reson Med,1996,36(1):159-165.

[13] Morrell G,Spielman D.Dynamic shimming for multi-slice magnetic resonance imaging[J].Magn Reson Med,1997,38(3):477-483.

[14] de Graaf RA,Brown PB,McIntyre S,et al.Dynamic shim updating (DSU) for multislice signal acquisition[J].Magn Reson Med,2003,49(3):409-416.

[15] Yang QX,Dardzinski BJ,Li S,et al.Multi-gradient echo with susceptibility inhomogeneity compensation (MGESIC):demonstration of fMRI in the olfactory cortex at 3.0 T[J].Magn Reson Med,1997,37(3):331-335.

[16] Yang QX,Williams GD,Demeure RJ,et al.Removal of localɦeld gradient artifacts in T2*-weighted images at high ɦelds by gradient-echo slice excitation profile imaging[J].Magn Reson Med,1998,39(3):402-409.

[17] Constable RT,Spencer DD.Composite image formation in z-shimmed functional MR imaging[J].Magn Reson Med,1999,42(1):110-117.

[18] Deichmann R,Josephs O,Hutton C,et al.Compensation of susceptibility-induced BOLD sensitivity losses in echo-planar fMRI imaging[J].Neuroimage,2002,15(1):120-135.

[19] Michal CA.Magnetic field homogeneity: A new approach to orthogonalizing and optimizing shim gradients[J].J Magn Reson,2007,185(1):110-117.

[20] Vanzijl PCM,Sukumar S,Johnson MO,et al.Optimized shimming for high-resolution nmr using 3-dimensional imagebased ɦeld-mapping[J].JMRI,1994,111(2):203-207.

[21] Barjat H,Chilvers PB,Fetler BK,et al.A practical method for automated shimming with normal spectrometer hardware[J].J Magn Reson,1997,125(1):197-201.

[22] Evans CL,Morris GA,Davis AL.A new method for variable temperature gradient shimming[J].J Magn Reson,2002,154(2):325-328.

[23] Hedley M,Rosenfeld D.A new two-dimensional phase unwrapping algorithm for mri images[J].Magn Reson Med,1992,24(1):177-181.

[24] Weiger M,Speck T,Fey M.Gradient shimming with spectrum optimisation[J].J Magn Reson,2006,182(1):38-48.

[25] Axel L,Morton D.Correction of phase wrapping in magnetic resonance imaging[J].Med Phys,1989,16(2):284-287.

[26] 俎栋林.核磁共振成像仪：构造原理和物理设计[M].北京:科学出版社,2015.