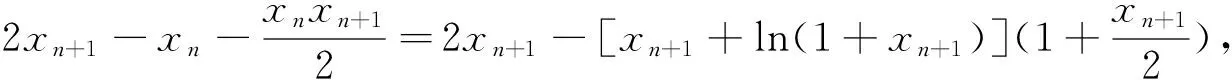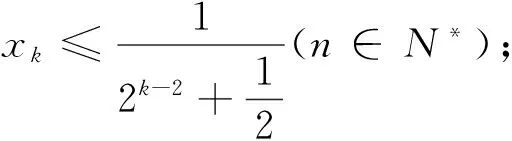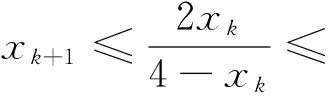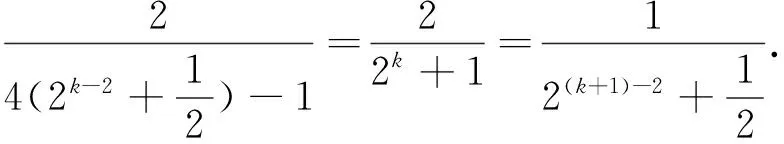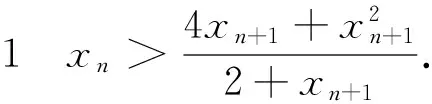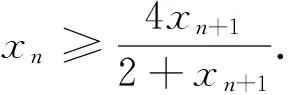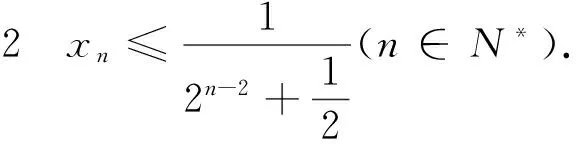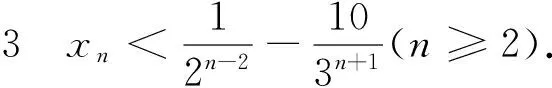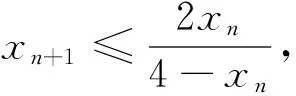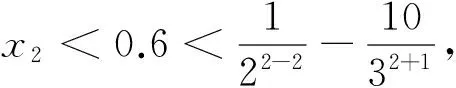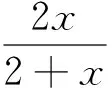一道高考压轴题的探究

浙江省宁波市效实中学 (315012) 吕孙忠

1.原题呈现

2017年浙江高考理科数学的压轴题为：

已知数列{xn}满足x1=1，xn=xn+1+ln(1+xn+1)(n∈N*).证明：n∈N*时，

(1)0

2.解法探究

2.1 第1问解答

分析：问题(1)的起步是比较低的，所以解题者起步的心情也是比较愉悦的.最容易想到的就是使用数学归纳法.

解法1:(数学归纳法)先证明xn>0，n∈N*.用数学归纳法，当n=1时，命题显然成立，设当n=k，k∈N*时命题成立，即xk>0，则考虑函数f(x)=x+ln(1+x)是单调递增函数，且有f(0)=0，xn=f(xn+1)，所以f(0)

解法2:(反证法)假设-10.

下同解法一.

2.2 第2问解答

分析：第2问的高等数学背景其实就是泰勒展开，如果解题者通过作差，再构造函数求导，那么过度会比较自然.

2.3 第3问解答

分析：第3问是该问题的核心和精髓部分.直接用数学归纳法的话，其实就进入了解题的陷阱，并且第3问的解答还用到了第2问的结论，这是浙江高考题的一贯特色.

3加强与推广

3.1 第2小问加强

3.2 第3小问加强

3.3 改编和推广

结论4 将x1=1改为x1>0，原数列单调递减收敛于0；将x1=1改为x1=-1，原数列单调递增收敛于0.

4.背景分析

一般情况下，我们需要用到一些重要结论对函数进行放缩，寻找到合适的隔离函数.下面，主要谈一谈ln(1+x)与ex有关的函数不等式结论.