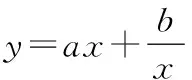曲线(A1x+B1y+C1)(A2x+B2y+C2)=D的特征与活用

浙江省宁波市北仑明港中学 (315806) 甘大旺

我们熟知，在直角坐标系xOy中，方程xy=m(常实数m≠0)表示双曲线；进一步认知，方程(x-a)(y-b)=m(常实数m≠0)仍然表示双曲线.再深入一个层次，笔者顿悟到：

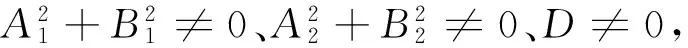
证明：由于A1B2≠A2B1，则两条直线A1x+B1y+C1=0和A2x+B2y+C2=0相交.取这两条相交直线的交点(x0,y0)为新坐标原点O′，取其夹角平分线为x′轴，建立直角坐标系x′O′y′.

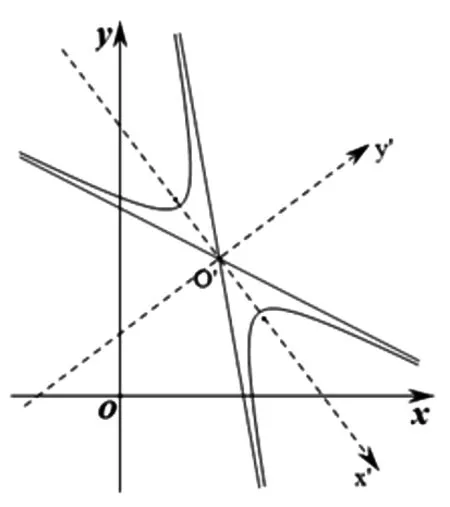
图1

如图1，存在对原坐标系xOy实施旋转、平移的唯一复合变换

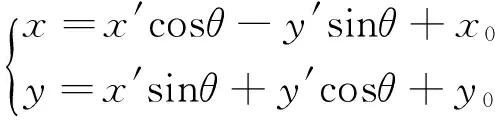
在直角坐标系x′O′y′中，方程(Ⅱ)表示双曲线，且两条渐近线方程是Ax′+By′=0和Ax′-By′=0.所以，回归到直角坐标系xOy中，方程(Ⅰ)表示双曲线，且两条渐近线是直线A1x+B1y+C1=0和A2x+B2y+C2=0.证毕.

在上面的证明过程中，假如取两条相交直线A1x+B1y+C1=0和A2x+B2y+C2=0的夹角平分线为y′轴，仍然取其交点(x0,y0)为新坐标原点O′，建立直角坐标系x′O′y′，则同理可证结论.此外，用判别式法只可识别方程(Ⅰ)表示双曲线.

下面列举两例，显示定理1的实用价值.

例1 (2014年南开大学数学试点班自主招生题)设P为曲线2x2-5xy+2y2=1上的动点，求点P到原点距离的最小值.

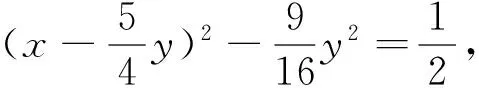
联立y=x与2x2-5xy+2y2=1构成方程组，代入消去y得x2=-1，这自相矛盾，舍去；

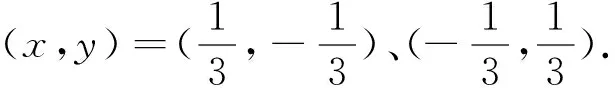
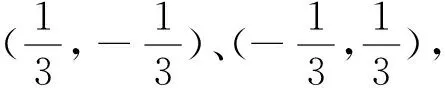
评注：①双曲线的对称中心到其上动点的最小距离等于对称中心到其顶点的距离；②双曲线的顶点在两条渐近线夹角的内角平分线或外角平分线上.

例2 (2017年清华大学首次高中生标准学术能力测试数学题)已知实数x、y满足5x2-y2-4xy=5，则2x2+y2的最小值等于( ).

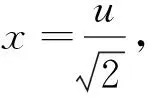
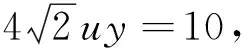
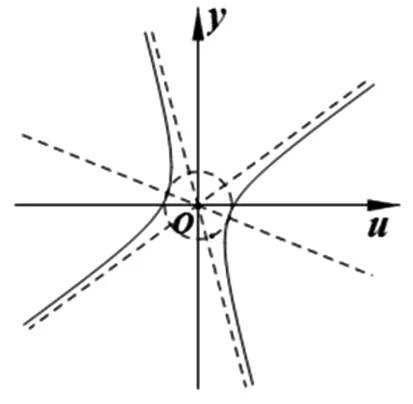
图2

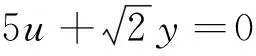
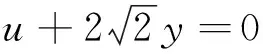
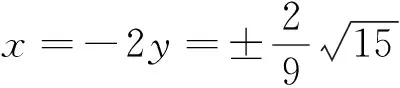
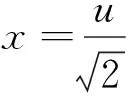
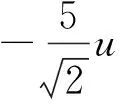
回顾例1、例2解题过程的开始两步变式，不难推测并运用定理1验证得到：

推论在定理1的相同条件下，二次方程(A1x+B1y+C1)2-(A2x+B2y+C2)2=D表示双曲线.

将此推论类比到椭圆和抛物线中去思考，容易拾遗并可验证一个相伴结论：

定理2 在定理1的相同条件下，二次方程(A1x+B1y+C1)2+(A2x+B2y+C2)2=D、(A1x+B1y+C1)2=A2x+B2y+C2(其中D>0)分别表示椭圆或圆、抛物线.