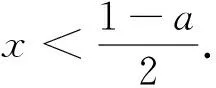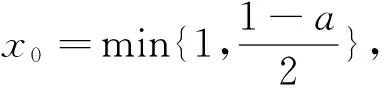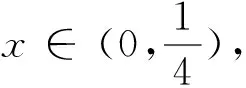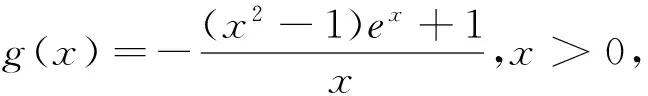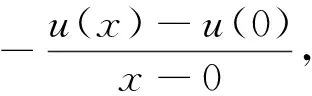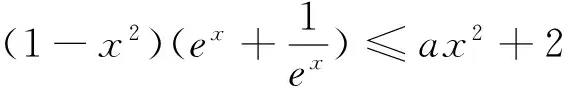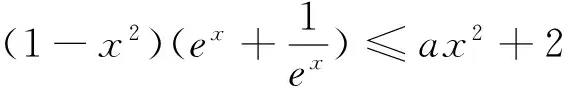2017年高考全国Ⅱ卷文科压轴题的另解及变式

湖南省桃江县第一中学 (413400) 胡芳举

2017年高考全国卷Ⅱ文科压轴题为:

设函数f(x)=(1-x2)ex.

(Ⅰ)讨论f(x)的单调性;

(Ⅱ)当x≥0时,f(x)≤ax+1,求a的取值范围.

本文将给出(Ⅱ)的多种解法以及一个变式.

分析一：分两步.

(1)设g(x)=(x2-1)ex+ax+1,x≥0，则f(x)≤ax+1⟺(x2-1)ex+ax+1≥0⟺g(x)≥0⟺g(x)≥g(0)，又x≥0，由此想到：若g(x)单调递增，则f(x)≤ax+1必成立.

∵g′(x)=(x2+2x-1)ex+a，g′′(x)=(x2+4x+1)ex>0，∴g′(x)单调递增.∴g(x)单调递增⟺g′(x)=(x2+2x-1)ex+a≥0⟺g′(0)≥0⟺a≥1.∴当a≥1时，f(x)≤ax+1恒成立.

(2)当a<1时，f(x)≤ax+1恒成立吗？如何分析呢？利用函数的连续性.

注意到g′(0)=a-1<0，故由函数g′(x)的连续性知：∃x0>0，当x∈(0,x0)时，g′(x)<0，∴g(x)单调递减，∴当x∈(0,x0)时，g(x)

方法2:要证明：当a<1时，f(x)≤ax+1不恒成立，等价于证明g(x)≥0不恒成立,只需证明g(x)<0有解，注意到g(0)=0，故只需证明g(x)在x=0右侧附近存在减区间，即∃x0>0，当x∈(0,x0)时，g′(x)<0.

方法3:g′(0)=a-1<0，若g′(1)≤0，则由g′(x)单调知：当x∈(0,1)时，g′(x)<0，从而g(x)0，则∃x0∈(0,1)时，使g′(x0)=0，同上知：当x∈(0,x0)时，g(x)<0.

说明:这种题型的解法，要注意两点：首先要注意到g(0)=0，其次是利用函数的连续性分析“当a<1时，不等式f(x)≤ax+1不恒成立”.

分析二:先分参，再转化为函数最值.

f(x)≤ax+1⟺(x2-1)ex+ax+1≥0⟺a≥

令u(x)=(x2-1)ex,则g(x)=

当a≥-1时，f″(x)≥0，f′(x)单调递增，∴f′(x)≥f′(0)=0，f(x)单调递增，∴f(x)≥f(0)=0，不等式恒成立.当a<-1时，f″(0)=2a+2<0，同方法3知：∃x0>0，当x∈(0,x0)时，f″(x)<0，f′(x)单调递减，∴f′(x)

综上，a≥-1.